Расчет на разрыв металла
Расчет угловых сварных швов на прочность обязателен при любом напряженно- деформированном состоянии элемента. Как уже отмечалось при рассмотрении основных видов сварных швов, и при растяжении, и сжатии, и при изгибе, и в любом другом напряженном состоянии рассматриваемого элемента конструкции на одном из катетов углового сварного шва всегда будут действовать касательные напряжения.
При этом на второй катет сварного шва могут действовать растягивающие (сжимающие) нормальные напряжения и (или) касательные напряжения в зависимости от напряженно деформированного состояния рассматриваемого элемента конструкции и положения шва в пространстве.
В целом основные положения, принимаемые при расчете угловых сварных швов, такие же как и при расчете остальных элементов конструкции.
Так как сопротивление металла сдвигу или срезу при действии касательных напряжений значительно меньше сопротивления растяжению, сжатию или изгибу при действии нормальных напряжений, то расчет угловых сварных швов (расчет на условный срез) сводится к определению касательных напряжений, которые должны быть меньше расчетного сопротивления.
Предполагается, что разрушение углового сварного шва может произойти в двух плоскостях: по металлу шва и по границе сплавления, поэтому расчет угловых швов производится для этих двух сечений:

Рисунок 529.3. Расчетные сечения угловых швов
А теперь рассмотрим возможные напряженные состояния элементов, соединяемых угловыми швами, более подробно.
Расчет угловых сварных швов производится по следующим формулам:
1. Расчет угловых швов при центральном растяжении (рисунок 529.2.д)) или сжатии (действии силы N)

Рисунок 529.2. Основные виды сварных соединений с угловыми швами.
И лобовые и фланговые швы рассчитываются на условный срез
1.1. по металлу шва (сечение 1 на рисунке 529.3):
где N - значение продольной растягивающей (или сжимающей) силы, приложенной по оси, совпадающей с центром тяжести сечения (без эксцентриситета). Может измеряться в кгс, тс, Н, кН;
βf - безразмерный коэффициент, определяемый по следующей таблице:
Таблица 529.2. (согласно СНиП II-23-81* "Стальные конструкции")

Примечание: почему при расчетах я рекомендую пользовать именно этой таблицей, а не таблицей из актуализированной редакции указанного СНиПа, достаточно подробно объясняется в статье, посвященной рассмотрению основных видов сварных швов.
kf - катет углового шва. Принимается по конструктивным требованиям или согласно расчету. Измеряется в мм или см.
lw - суммарная длина угловых швов с учетом непровара в начале и в конце шва. Например, если рассчитывается один угловой шов длиной l, то его расчетная длина составит:
lw = l - 2t (529.1.1)
где t - толщина наименьшей из свариваемых деталей.
В целом произведение βfkflw - это и есть площадь рассматриваемого сечения.
Rwf - расчетное сопротивление срезу по металлу шва. Определяется по следующей таблице:
Таблица 530.2. Расчетные сопротивления сварных соединений (согласно СП 16.13330.2011 "Стальные конструкции")

Примечания:
1. Значения коэффициентов надежности по металлу шва γwm следует принимать:
γwm = 1,25 - при Rwun ≤ 490 Н/мм 2 (4900 кг/см 2 );
γwm = 1,35 - при Rwun ≥ 590 Н/мм 2 (5900 кг/см 2 )
Значения Rwun и Rf определяются по следующей таблице:
Таблица 531.1. (согласно СП 16.13330.2011 "Стальные конструкции")

Примечание:
В ныне неактуальном СНиП II-23-81* и старых справочниках, таблица вида 530.2 сопровождалась следующими примечаниями:
1. Для угловых швов, выполняемых ручной сваркой, значения Rwun принимают равными значениям временного сопротивления разрыву металла шва (σв) согласно ГОСТ 9467-75*.
Приводить здесь таблицу из ГОСТа, по которой можно определить временное сопротивление разрыву шва, я не буду. Просто скажу, что в маркировке электродов это значение уже указано в кгс/мм 2 . Например:
- для электродов Э38 Rwun = σв = 38 кгс/мм 2 (3800 кгс/см 2 )
- для электродов Э42А Rwun = σв = 42 кгс/мм 2 (4200 кгс/см 2 ) и так далее вплоть до Э150 (сейчас такие марки электродов даже и не рассматриваются).
На мой взгляд это учень удобно, тем не менее сейчас все принято выражать в единицах системы СИ, что и отображено в таблице 531.1.
γс - коэффициент условий работы элементов конструкций и соединений, принимаемый по следующей таблице:
Таблица 530.3. Коэффициенты условий работы элементов и соединений стальных конструкций (согласно СП 16.13330.2011 "Стальные конструкции")

1.2. По металлу границы сплавления (сечение 2 на рисунке 529.3):
где βz - безразмерный коэффициент, определяемый по таблице 529.2.
Rwz - расчетное сопротивление металла на границе сплавления, определяемое по таблице 530.2, где Run - нормативное сопротивление проката, определяемое по следующей таблице:
Таблица 171.8. (согласно ГОСТ 27772-88 для стальных конструкций зданий и сооружений)
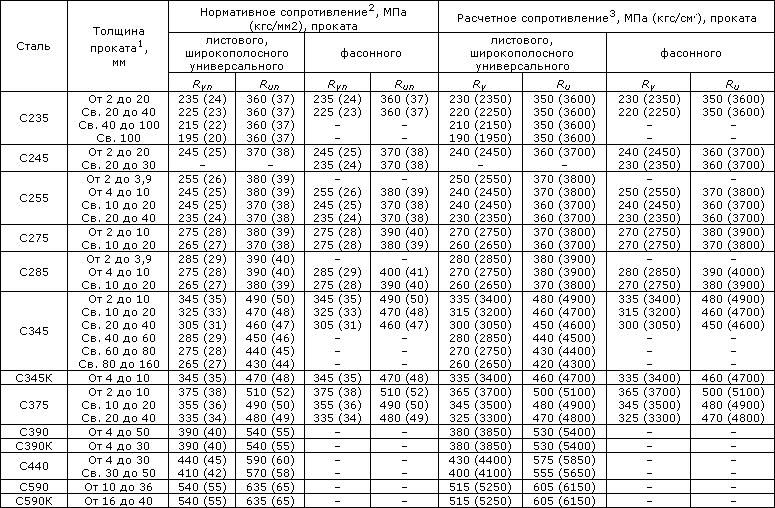
Примечание: заменяемые марки стали приводятся отдельно.
Тут добавлю, что при центральном растяжении или сжатии элемента из свариваемых деталей во фланговых швах на обеих катетах шва будут действовать касательные напряжения. В лобовых швах на одном из катетов будут действовать растягивающие или сжимающие нормальные напряжения, имеющие такое же значение, как и касательные напряжения на втором катете.
Я это все к тому, что иногда в справочниках напряжения, определяемые для других видов напряженно-деформированного состояния обозначаются как нормальные, т.е. литерой "σ". Формально тут большой ошибки нет и делается это больше для того, чтобы различать напряжения, возникающие при действии изгибающего момента и других возможных воздействий. Но все равно нельзя забывать, что расчет производится именно на условный срез, т.е. на действие касательных напряжений, имеющих, впрочем, такое же значение, как нормальные на втором катете. А вот направления действия касательных напряжений действительно могут быть разными, что мы вскоре и увидим.
2. Расчет сварных соединений с угловыми швами при действии изгибающего момента М в плоскости, перпендикулярной плоскости расположения швов
Т.е. в данном случае имеется в виду, что через рассматриваемые швы можно провести одну плоскость и эта плоскость будет перпендикулярна плоскости действия момента. К положению плоскости, в которой может произойти разрушение шва, данная формулировка никакого отношения не имеет.
Как правило такая ситуация возникает при расчете сварного соединения втавр двухсторонними швами (рисунок 529.2.г)) или односторонними швами (рисунок 529.3). При этом угловые швы рассчитываются на условный срез
2.1. по металлу шва (сечение 1 на рисунке 529.3):
2.2. по металлу границы сплавления (сечение 2 на рисунке 529.3):
где М - значение изгибающего момента, определяемое по эпюре "М".
Wf и Wz - моменты сопротивления расчетных сечений сварного соединения по металлу шва и по границе сплавления с металлом соответственно.
Например при соединении втавр двухсторонними швами моменты сопротивления составят:
Как правило, разделив момент М на момент сопротивления W, мы определяем нормальные напряжения, поэтому в некоторых старых учебниках и справочниках (например: А.П.Мандриков, Примеры расчета металлических конструкций, М.-1991) формулы (531.3) и (531.4) имеют другую форму записи, примерно такую:
Но сути это не меняет.
1. В СНиП II-23-81* и старых справочниках значение расчетного сопротивления Rwf и Rwz при всех возможных расчетных случаях дополнительно умножалось на коэффициенты условий работы шва γwf или γwz соответственно.
Значение этих коэффициентов принималось равным 1 во всех случаях, кроме конструкций, возводимых в климатических районах I1 (согласно ГОСТ 16350-80: очень холодный, среднемесячная температура воздуха в январе от -50 до -30), I2 (холодный, температура от -30 до -15), II2 (арктический восточный, температура от -28 до -18) и II3 (арктический западный, температура от -30 до -2), для которых γwf = 0.8 при Rwun = 410 МПа и γwz = 0.85 для всех сталей.
На мой взгляд данное ограничение значения расчетного сопротивления вводилось с целью уменьшения риска хрупкого разрушения сварного соединения при низких температурах. Сейчас оно не действует, но думаю, знать о нем надо.
2. Вообще-то это примечание следовало сделать при рассмотрении первого раздела, но он и так получился перенасыщенным информацией, поэтому оставлю это примечание здесь.
3. Расчет угловых швов при действии изгибающего момента М в плоскости, перпендикулярной плоскости швов и действии продольной силы N
Подобная ситуация часто встречается при расчете разного рода опорных площадок, поэтому я выделил ее в отдельный раздел, хотя в СП 16.13330.2011 такой вариант загружения отдельно не рассматривается.
Тем не менее, при загружении опорной площадки некоторой силой, приложенной с эксцентриситетом, возникает следующая ситуация, которую я решил проиллюстрировать картинкой из все того же А.П.Мандрикова:

Рисунок 531.1.
В этом случае угловые швы рассчитываются на условный срез
3.1. по металлу шва:
3.2. по металлу границы сплавления:
где значение касательных напряжений определяется в зависимости от рассматриваемого сечения по формулам (531.1) и (531.2), а значение условно нормальных напряжений - по формулам (531.3.2) и (531.4.2) соответственно.
Конечно же согласно требований ныне действующих нормативных документов более правильно вести речь только о касательных напряжениях относительно осей х и у. Т.е. тwf = тy, σwf = тх и так далее, но как уже говорилось, на окончательные результаты расчета это ни как не влияет, при этом старый подход выглядит более наглядным.
4. Расчет угловых швов при действии изгибающего момента М в плоскости сварных швов
Подобная ситуация часто встречается при расчете стыковых соединений с накладками, т.е. при одновременном использовании и лобовых и фланговых швов (см. рисунок 529.2.в)), а также при соединении внахлест лобовыми или фланговыми швами (см. рисунок 529.2.а) и б)). Это означает, что как и в предыдущем случае касательные напряжения действуют как вдоль оси х, так и вдоль оси у. Соответственно задача сводится к определению равнодействующей этих двух напряжений. Расчет в этом случае выполняется по следующим формулам:
4.1. по металлу шва:
4.2. по металлу границы сплавления:
где х и у - координаты рассматриваемой точки сварного соединения относительно главных осей х-х и у-у. Как правило рассматриваемая точка максимально удалена от центра тяжести О расчетного сечения.
Ifx, Ify, Izx, Izy - моменты инерции рассматриваемых сечений швов относительно главных осей.
Так как рассчитываемые швы находятся в одной плоскости с действующим моментом, то для определения указанных моментов инерции необходимо кроме катета, длины шва и соответствующих коэффициентов также знать расстояние между швами, чего не требовалось при рассмотрении швов, находящихся в плоскости, перпендикулярной плоскости действия момента.
В нормативных документах вопросу определения моментов инерции для угловых сварных швов внимания не уделяется, но на мой взгляд это достаточно сложный вопрос и вообще его рассмотрению следует посвятить отдельную статью, а пока ограничимся следующим примером:
При соединении внахлест только лобовыми швами и при расстоянии между центрами тяжести лобовых швов, равном l (центры тяжести и расстояние l на рисунке 529.2.а) не показаны), значения моментов инерции для сечения металла шва составят:
5. Расчет угловых швов при действии момента М, продольной N и поперечной V сил в плоскости сварных швов
Это наиболее общий случай напряженно-деформированного состояния, проиллюстрированный в СП 16.13330.2011 следующим образом:

Рисунок 531.2. Расчетная схема сварного соединения с угловыми швами в общем случае загружения.
Расчет в этом случае выполняется по следующим формулам:
5.1. по металлу шва:
5.2. по металлу границы сплавления:
где тf и тz - касательные напряжения в рассматриваемой точке расчетного сечения сварного соединения по металлу шва и по металлу границы сплавления, определяемые по формуле:
где тN и тV - касательные напряжения, определяемые по формулам (531.1) и (531.2), а тМх и тМу - горизонтальная и вертикальная составляющие касательных напряжений при действии момента, определяемые по следующим формулам:
Но и это еще не все. При проектировании строительных конструкций необходимо также соблюдать конструктивные требования, предъявляемые к сварным соединениям.
На этом пока все.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье "Записаться на прием к доктору"
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Для Украины - номер гривневой карты (Приватбанк) 5168 7422 4128 9630
Рассчитать формулу нахлесточное соединения
Доктор, как увязать формулы 531.7(8) с формулами 531.14 и 531.15. Судя по всему в знаменателе должна быть сумма моментов инерции тМх = М*х/(Iy+Ix) и тМу = М*у/(Iy+Ix). В подтверждение предлагаю книгу: Металлические конструкции (вопросы и ответы), Бирюлев В.В., страница 56
Судя по чему? Будьте добры, распишите более подробно. Можете цитировать Бирюлева В.В.
При N=0 и Q=0 формула (531.13) т = ((тN + тМх)^2 + (тV + тМу)^2)^1/2 при знаменателе (Iy+Ix) примет вид т = ((М*х/(Iy+Ix))^2 + (М*х/(Iy+Ix))^2)^1/2 и сведется к формуле (531.7) тМ = М(х^2 + у^2)^1/2/(Ix + Iy). У господина Бирюлева (книга есть на двг.ру) тxM = M*r*cos(a)/(Ify+Ifx), тyM = M*r*sin(a)/(Ify+Ifx), где r=(х^2 + у^2)^1/2, cos(a)=y/r, sin(a)=x/r, соответственно тxM = M*r*(y/r)/(Ify+Ifx), тyM = M*r*(x/r)/(Ify+Ifx). Хмм. не заметил даже, что x и y наоборот у него, так что по Бирюлеву тМх = М*y/(Iy+Ix) и тМу = М*x/(Iy+Ix)
Так уже значительно лучше. Если я правильно понял господина Бирюлева в вашем изложении, то после сокращения формул тxM = M*r*(y/r)/(Ify+Ifx), тyM = M*r*(x/r)/(Ify+Ifx) получается, что тxM = M*y/(Ify+Ifx), тyM = M*x/(Ify+Ifx), где f - это символ функции. А аргумент функции и значение функции - это вроде бы разные вещи. Поэтому ваш логический переход Ify+Ifx = Iy+Ix пока ничем не обоснован с чисто математической точки зрения. Обоснуйте.
Хорошо, avatar, развивайте свою мысль: если формулы 531.14 и 531.15 неправильные (как вы утверждаете), то значит и с остальными формулами что-то не так. Например, формула σwf = М/Wf ≤ Rwfγc (531.3.2) по вашей логике должна выглядеть так: σwf = М/(Wfх + Wfу) ≤ Rwfγc. Где ошибка?
И тут не нужны какие-то доп.картинки, формулы и примеры расчетов - это все теория, которую следует подтверждать практикой. А для научного диспута, который мы тут затеяли, вполне достаточно 4 картинок, которые есть в данной статье, общих знаний строймеха и сопромата, ну и конечно же - геометрии, без нее никуда.
Ошибка в том, что формула нормального напряжения (531.3.2) относится к напряжению от действия момента в плоскости, перпендикулярной плоскости швов, а формула касательных напряжений (531.7) - к действию момента в плоскости швов. Например, формула тМ = М(х2 + у2)1/2/(Ifx + Ify) ≤ Rwfγc (531.7) по вашей логике должна выглядеть так: тМ = ((Mx/Iy)^2 + (My/Ix)^2)^1/2 = M((x/Iy)^2 + (y/Ix)^2)^1/2. Где ошибка?
И это далеко не научный дискурс. Просто мне было интересно, откуда молодой инженер взял эти формулы.
Я деменцию бесплатно не лечу, тем более в таком запущенном состоянии. Хочешь лечиться - запишись на прием, нет - до свидания. И да, если действительно хочешь лечиться, то сначала сам разберись:
1. Вокруг какой оси вращает момент поперечное сечение шва в первом и во втором случае?
2. Чем крутящий момент отличается от изгибающего и какой более простой формулой можно заменить формулу (531.7)?
3. Что такое площадки напряжений и как суммируются нормальные и касательные напряжения на главных площадках при плоском напряженном состоянии хотя бы по первой теории прочности?
Для начала хватит. Задачку по геометрии ты решил правильно, поэтому не безнадежен.
А зачем дурик усы сбрил или откуда молодой инженер взял формулы - это ты у Петровича спроси, может он знает. Ему пациенты такие вопросы часто задают.
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье "Записаться на прием к доктору" (ссылка в шапке сайта).
2.4. Расчеты на прочность при растяжении



2.4. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ РАСТЯЖЕНИИ Основной задачей расчета конструкции на растяжение является обеспечение ее прочности в условиях эксплуатации. Условие прочности – оценка прочности элемента конструкции, сводящаяся к сравнению расчетных напряжений с допускаемыми: σ≤рσ[р ]; σ с ≤[ с],σ (2.9) где σр и σс – наибольшие расчетные растягивающие и сжимающие напряжения; [σр] и [σс] – допускаемые напряжения при растяжении и сжатии. Допускаемое напряжение – наибольшее напряжение, которое можно допустить в элементе конструкции при условии его безопасной, долговечной и надежной работы: Здесь σпред – предельное напряжение (состояние), при котором конструкция перестает удовлетворять эксплуатационным требованиям; им мо- гут быть предел текучести, предел прочности, предел выносливости, пре- дел ползучести и др. Для конструкций из пластичных материалов при определении допускаемых напряжений используют предел текучести σт (рис. 2.4, а). Это связано с тем, что в случае его превышения деформации резко возрастают при незначительном увеличении нагрузки и конструкция перестает удовлетворять условиям эксплуатации. Допускаемое напряжение в этом случае определяют как Для хрупких материалов (чугун, бетон, керамика) где σвр и σвс – пределы прочности при растяжении и сжатии (рис. 2.4, б). Здесь [n] – нормативный коэффициент запаса прочности. В зависимости от той предельной характеристики, с которой сравнивают расчетное напряжение σ, различают [nт] – нормативный коэффициент запаса прочности по отношению к пределу текучести σт и [nв] – нормативный коэффициент запаса прочности по отношению к пределу прочности σв. Запас прочности – отношение предельно допустимой теоретической нагрузки к той нагрузке, при которой возможна безопасная работа конструкции с учетом случайных перегрузок, непредвиденных дефектов и недостоверности исходных данных для теоретических расчетов. Нормативные коэффициенты запаса прочности зависят: − от класса конструкции (капитальная, временная), − намечаемого срока эксплуатации, − условий эксплуатации (радиация, коррозия, загнивание), − вида нагружения (статическое, циклическое, ударные нагрузки) − неточности задания величины внешних нагрузок, − неточности расчетных схем и приближенности методов расчета − и других факторов. Нормативный коэффициент запаса прочности не может быть единым на все случаи жизни. В каждой отрасли машиностроения сложились свои подходы, методы проектирования и приемы технологии. В изделиях общего машиностроения принимают [nт] = 1,3 – 2,2; [nв] = 3 – 5. Вероятность выхода из строя приближенно можно оценить с помощью коэффициента запаса в условии прочности: n = 1 соответствует вероятности невыхода из строя 50 %; n = 1,2 соответствует вероятности невыхода из строя 90 %; n = 1,5 соответствует вероятности невыхода из строя 99 %; n = 2 соответствует вероятности невыхода из строя 99,9 %. Для неответственных деталей n = 2 много. Для ответственных – мало. Так для каната подъемного лифта это означает на 1000 подъемов одно падение. При расчете конструкций на прочность встречаются три вида задач, которые вытекают из условия прочности а) поверочный расчет (проверка прочности). Известны усилие N и площадь A. Вычисляют σ = N/A и, сравнивая его с предельным σт или σв (для пластичного и хрупкого материалов соответственно), находят фактический коэффициент запаса прочности который затем сопоставляют с нормативным [n]; б) проектный расчет (подбор сечения). Известны внутреннее усилие N и допускаемое напряжение [σ]. Определяют требуемую площадь поперечного сечения стержня в) определение грузоподъемности (несущей способности). Известны площадь А и допускаемое напряжение [σ]. Вычисляют внутреннее усилие N≤N[ ] = ⋅[σ]A, (2.15) а затем в соответствие со схемой нагружения – величину внешней нагрузки F ≤ [F].
Расчеты на прочность
Эта статья будет посвящена основным видам расчётов на прочность, которые выполняются в рамках дисциплины – «сопротивление материалов».
Виды расчетов на прочность
Существует два основных типа расчета на прочность: проверочный и проектировочный.
Проверочные расчеты на прочность – это такие расчеты, при выполнении которых проверятся прочность элемента конструкции, заданной формы, размеров и материала, под некоторой нагрузкой.
При проведении проектировочных расчетов на прочность определяются определённые размеры элемента конструкции (детали) из условия прочности. Причем, очевидно, что для разных видов деформаций эти условия прочности различны.
Также иногда выполняются расчеты на грузоподъемность, когда вычисляется максимальная нагрузка, которую может выдерживать конструкция.
Расчеты на прочность при растяжении (сжатии)
Начнём, пожалуй, с самого простого вида деформации – растяжения (сжатия).
Условие прочности
Условие прочности при растяжении (сжатии) выглядит следующим образом:
То есть рассчитываемый элемент можно считать прочным, если максимальное нормальное напряжение ( σmax ) возникающее в элементе меньше, либо, по крайней мере, равно допустимому — [σ] .
Нормальные напряжения ( σ ) в сечениях определяются по формуле:
где N – продольная сила в сечении;
A – площадь сечения.
Площадь простых сечений можно посчитать по этим формулам.
Допустимое напряжение
Как правило, в задачах, допустимое напряжение [σ] уже задано по условию. Для стали, по традиции, принимают [σ] = 160 МПа.
Если же [σ] , по условию задачи не дано явно, то допустимое напряжение можно вычислить по формуле:
где σ пред – предельное напряжение;
n – коэффициент запаса прочности.
Очевидно, за предельное напряжение для разных материалов принимают различное значение. Для пластичных материалов, например, для малоуглеродистой стали (Ст2, Ст3) принимают предел текучести , а для хрупких материалов (бетон, чугун) берут в качестве предельного напряжения – предел прочности (временное сопротивление). Эти характеристики получают при испытании образцов на растяжение (сжатие), с помощью специальных машин, которые фиксируют характеристики материалов в виде диаграмм.
Коэффициент запаса прочности ( n ) выбирается конструктором исходя из своего личного опыта, назначения или сферы применения проектируемой детали. Обычно коэффициент запаса прочности варьируется от 2 до 6 .
Проверка прочности при растяжении (сжатии)
Проверим прочность стального стержня, работающего на сжатие, если d1 = 50 мм, d2 = 70 мм, σт = 260 МПа, nт = 2.

Определим продольные силы на участках:

Определим площади поперечных сечений на участках:

Найдем нормальные напряжений на участках:

Максимальные нормальные напряжения будут равны:

Проверка прочности стержня
Определим допускаемое напряжение:


Прочность стержня обеспеченна.
Подбор размеров поперечных сечений при растяжении (сжатии)
Подберём размеры поперечных сечений стержня, если допустимое напряжение [σ] = 160 МПа.

Найдём продольные силы на каждом участке:


Запишем условие прочности для участков бруса:

Или его можно записать как:

Отсюда можно выразить необходимую площадь поперечных сечений:

Так как сечения бруса круглые, можно записать:

Подставляя численные значения для каждого участка, найдём искомые размеры:

Округлим полученные значения по ГОСТ 6636-69 (Ra40) до ближайших больших и окончательно примем:

Расчеты на прочность при кручении
При кручении расчёты на прочность в целом похожи на расчёты при растяжении. Только здесь вместо нормальных напряжений расчёт ведётся по касательным напряжениям .
На кручение, как правило, работают детали, которые называются валами. Их назначение – передача крутящего момента от одного элемента к другому. При этом вал по всей длине имеет либо круглое сечение, либо кольцевое.
За допустимое касательное напряжение [τ] , часто в задачах по сопромату, принимают напряжение в два раза меньше, чем допустимое нормальное напряжение [σ] :
Максимальные касательные напряжения ( τmax ) в сечениях можно найти по формуле:
где T – крутящий момент в сечении;
Wp – полярный момент сопротивления сечения.
Полярные моменты сопротивления
Полярные моменты сопротивления обозначаются буквой – W , с индексом p .
Полярный момент сопротивления круга
Полярный момент сопротивления кольца


Расчеты на прочность при изгибе
Теперь предлагаю поговорить о расчётах на прочность при поперечном изгибе. При этом виде деформации расчёты проводятся и по нормальным напряжениям и по касательным. Но так как зачастую касательные напряжения в несколько раз меньше нормальных, основным здесь является расчёт по нормальным напряжениям, а расчёт по касательным напряжениям — проверочный.
Условие прочности по нормальным напряжениям такое же, как и при растяжении (сжатии):
Нормальные напряжения в сечениях при поперечном изгибе, определяются по следующей формуле:
где Mизг – изгибающий момент в сечении;
W – момент сопротивления сечения;
Моменты сопротивления простых сечений
В этом разделе ты сможешь найти формулы для расчёта осевых моментов сопротивления сечений (фигур).
Моменты сопротивления обозначаются буквой – W .
Расчет на растяжение стержня
Расчет на прочность прямолинейного стержня при действии центрально приложенной растягивающей силы является одной из самых простых задач в теории сопротивления материалов.
Смысл данного расчета сводится к тому, чтобы обеспечить необходимую прочность материала, исходя из условия:
N/F = σ < Rр (525.1)
где N - продольная растягивающая сила, действующая на стержень;
F - площадь поперечного сечения стержня;
σ - нормальные напряжения, возникающие в рассматриваемом поперечном сечении стержня в ответ на действие растягивающей продольной силы;
Rр - расчетное сопротивление материала стержня растяжению (для некоторых материалов расчетные сопротивления растяжению, сжатию, изгибу и т.п. могут различаться).
Визуально это может выглядеть так:

Рисунок 525.1. Нормальные напряжения при растяжении прямолинейного стержня.
На рисунке 525.1.а) мы видим прямолинейный стержень длиной l, показанный серым цветом, к которому приложена растягивающая сила N. При этом точка приложения силы находится на нейтральной оси стержня, совпадающей с осью х, показанной пунктирной линией.
Для упрощения расчетов заменяем опору А соответствующей опорной реакцией А (рис.525.1.б). Исходя из условий статического равновесия:
∑х = А + N = 0 (149.5.2)
А = - N (525.2)
Это означает, что опорная реакция A равна по значению растягивающей силе N, но направлена в противоположную сторону.
Если взглянуть на эту ситуацию под некоторым углом, то она будет выглядеть так, как показано на рисунке 525.1.в). На этом рисунке мы видим, что нормальные напряжения - это реакция материала на действие растягивающей силы и направлены эти напряжения в сторону, противоположную действию сил. Другими словами нормальные напряжения препятствуют деформации растяжения, и направлены на то, чтобы вернуть материалу исходную форму. Иногда для упрощения восприятия нормальные напряжения, возникающие при растяжении, принято изображать направленными от сечения, как показано на рисунке 525.1.г), а сжимающие напряжения - направленными к сечению. С точки зрения физики такая замена вполне допустима, так как нормальные напряжения (внутренние силы) можно рассматривать как плоскую нагрузку, распределенную по всей площади сечения (внешнюю силу). Как правило растягивающие нормальные напряжения рассматриваются как положительные, а сжимающие - как отрицательные.
Сечение стержня, показанное на рисунке 525.1.в) розовым цветом, является перпендикулярным нейтральной оси стержня и называется поперечным сечением.
Как следует из формулы (525.1) и из приведенного рисунка, длина стержня l на значение нормальных напряжений никак не влияет. А вот параметры поперечного сечения стержня: ширина сечения b и высота сечения h, если сечение прямоугольное, очень даже влияют, так как от этих параметров зависит площадь F поперечного сечения.
Примечание: конечно же поперечное сечение стержня далеко не всегда имеет прямоугольную форму, как показано на рисунке 525.1.в). Поперечное сечение может быть и круглым, и овальным, и ромбическим, и вообще иметь любую сколь угодно сложную форму, тем не менее форма поперечного сечения никак на значение нормальных напряжений не влияет (во всяком случае такое допущение принимается в теории сопротивления материалов), а влияет только площадь сечения, определить которую тем сложнее, чем более сложной является форма поперечного сечения.
Проверить данные постулаты теории сопротивления материалов очень легко и просто. Достаточно взять нитку и попробовать ее разорвать (вариант а)). Затем разорвать нитки с с той же катушки, но б) более короткую и в) более длинную, чем в первом случае. Во всех трех случаях усилие, которое необходимо приложить для разрыва нитки, будет примерно одинаковым.
Но если одну из ниток сложить вдвое и попробовать разорвать, то усилие, необходимое для разрыва нитки, увеличится в 2 раза. Все потому, что условная площадь сечения стержня, работающего на растяжение, увеличится при складывании нитки в 2 раза.
Таким образом известная пословица: "где тонко, там и рвется" в переводе на язык теории сопротивления материалов будет звучать примерно так: "при действии растягивающих нормальных напряжений разрушение материала, обладающего постоянным сопротивлением растяжению по всей длине, будет происходить в сечении с минимальной площадью". Это особенно актуально для стержней с изменяющейся по длине площадью сечения.
С учетом различных факторов формула (525.1) может иметь другой вид:
где γn - коэффициент надежности по нагрузке (как правило больше единицы), Fn - минимальная площадь сечения (с учетом возможных ослаблений отверстиями, пазами и т.п.), γs - коэффициент условий работы (как правило меньше единицы).
Т.е. теория сопротивления материалов допускает, что нормальные напряжения в стержне могут быть равны расчетному сопротивлению материала на растяжение, умноженному на коэффициент условий работы.
Пример расчета стержня на растяжение
Дано: На стальной стержень (см. рис.525.1.а)) с расчетным сопротивлением Rp = 2250 кг/см 2 действует продольная растягивающая сила N = 30 тонн. Коэффициент надежности по нагрузке γn = 1.05, коэффициент условий работы γs = 0.9. Собственным весом стержня в виду его незначительности по сравнению с действующей нагрузкой для упрощения расчетов можно пренебречь. Предполагается, что нагрузка прикладывается по всей площади поперечного сечения стержня, т.е. возникающие нормальные напряжения будут равномерно распределенными по всей площади сечения.
Требуется: Подобрать диаметр стержня.
Решение:
1. Определяем требуемую площадь сечения стержня, преобразовав формулу (525.1.2)
F = Nγn/Rpγs = 30000·1.05/(2250·0.9) = 15.56 см 2 .
2. Определяем диаметр стержня
d = √ 4F/п = √ 4·15.56/3.14 = 4.45 см
Как видим сам расчет занимает гораздо меньше времени, чем описание физических характеристик используемых данных и даже формулировка условия задачи.
Читайте также:
