Расчет металлической стойки на устойчивость
Расположенный ниже онлайн калькулятор предназначен для расчёта центрально-нагруженной стойки (колонны) из стального проката круглого, квадратного, прямоугольного и шестигранного сечения на прочность, устойчивость и изгиб. Если Вам нужно рассчитать онлайн прочность, изгиб и устойчивость стойки из СТАЛЬНЫХ ТРУБ, смотрите ТУТ . Или расчет стойки из ШВЕЛЛЕРА, ДВУТАВРА, ТАВРА и УГОЛКА на прочность, устойчивость и гибкость.
При проектировании строительных конструкций, необходимо принимать схемы, обеспечивающие прочность, устойчивость и пространственную неизменяемость сооружения в целом, а также его отдельных элементов при монтаже и эксплуатации.
Поэтому стойку, находящуюся под действием сжимающей её нагрузки необходимо проверять:
- На прочность;
- Устойчивость;
- Допустимую гибкость.
Для расчета предлагаем вам воспользоваться онлайн калькулятором, специально разработанным для нашего сайта!
Онлайн калькулятор для расчёта стойки (колонны) из стального проката
Логика онлайн расчета на прочность и устойчивость стойки из стального проката
Согласно Актуализированной редакция СНиП II-23-81 (CП16.13330, 2011) рассчитывая на прочность элементов из стали при центральном растяжении или сжатии силой P следует выполнять по формуле:
P / Fp * Ry * Yc
- где P — действующая нагрузка.
- Fp — площадь поперечного сечения колонны.
- Ry — подсчетное сопротивление материала (стали колонны), выбирается по таблице В5 Приложения «В» того же СНиПа.
- Yc — коэффициент условий работы по таблице 1 СНиПа (0.9-1.1). В соответствии с примечанием к этой таблице (пункт 5) в калькуляторе принято Yc=1.
Проверку на устойчивость элементов сплошного сечения при центральном сжатии силой P следует выполнять по формуле:
P / Fi * Fp * Ry * Yc
где Fi — коэффициент продольного изгиба центрально — сжатых элементов.
Коэффициент Fi введён в качестве компенсации возможности некоторой не прямолинейности колонны, недостаточной жесткости её крепления и неточности в приложении нагрузки относительно оси стойки.
Значение Fi зависит от марки стали и гибкости колонны и часто берётся из таблицы 72 СНиП II-23-81 1990г., исходя из гибкости колонны и расчётного сопротивления выбранной стали сжатию, растяжению и изгибу.
Это несколько упрощает и огрубляет вычисления, так как СНиП II-23-81* предусматривает специальные формулы для определения Fi. Гибкость (Lambda) — некоторая величина, характеризующая свойства рассматриваемого стержня в зависимости от его длины и параметров поперечн. сечения, в частности радиуса инерции:
Lambda = Lr / i
- здесь Lr — расчётная длина стержня,
- i — радиус инерции поперечного сечения стержня (колонны).
Радиус инерции сечения i равен корню квадратному из выражения I / Fp, где I — момент инерции, Fp — его площадь.
Lr (расчётная длина) определяется как Mu*L; здесь L — длина стойки, а Mu — коэфф., зависящий от схемы её крепления:
- «заделка-консоль»(свободный конец) — Mu=2;
- «заделка-заделка» — Mu = 0.5;
- заделка — шарнир» — Mu = 0.7;
- «шарнир — шарнир» — Mu = 1.
Следует иметь ввиду,что при наличии у формы поперечн. сечения 2-ух радиусов инерции (например, у прямоугольника), при вычислении Lambda используется меньший.
Кроме того, сама Lambda (гибкость колонны), рассчитанная по формуле Lambda = Lr / i не должна превышать 220-ти в соответствии с таблицей 19. СНиП II-23-81*; там же содержатся ограничения на предельную гибкость центрально — сжатых стержней.
Для их использования необходимо сделать выбор в таблице онлайн калькулятора «Вид, назначение стоек». Предельная гибкость стоек, кроме их геометрических параметров, зависит также от коэффициента продольного изгиба (Fi), действующей нагрузки (P), расчётного сопротивления материала стоики (Ry) и условий её работы (Yc).
Предельная гибкость, устойчивость и прочность стоек, кроме их геометрических параметров, зависит также от коэффициента продольного изгиба (Fi), действующей нагрузки (P), расчётного сопротивления материала стойки (Ry) и условий её работы (Yc).
Если возникнут трудности при расчетах онлайн калькулятором прочности и устойчивости, рекомендуем предварительно ознакомиться с инструкцией.
Расчет на устойчивость стойки из металлической трубы
Здравствуйте! Хочу предоставить на обсуждение мой расчет на устойчивость. Мне важно мнение специалистов, т.к. все делал по справочникам и учебникам. Специального образования не имею, но жизнь заставляет и этим заниматься. Нашел два примера расчета : первый по допускаемому напряжению, второй по расчетному сопротивлению. На втором способе споткнулся. В чем моя ошибка?
боюсь спросить даже.
какого года источник примера.
давно уж допускаемые напряжения заменены расчетом по предельным состояниям
Пользовался учебником одного известного института 2008г. А как сейчас считают ? Какой литературой мне воспользоваться ?
Невозможно подобрать сечение которое соответсвовало бы расчетному напряжению. А перенапряжение допускается 5%. Примечания писал для анализа.
На счет 5% не сорю - это было всегда. Просто уточняю - расчет смотрел бегло - почему в одной формуле перенапряжение, во второй недонапряжение для одного и того же элемента?
__________________| --- Обращение ко мне - на "ты". Все, что сказано - личное мнение. |
To Emerald: Вы очевидно пользовались учебником по сопротивлению материалов. Сопротивление материалов - наука универсальная, и ее методы применяются не только в строительстве, но и во многих других областях. В сопромате и в этих самых областях применяется обычно метод по допустимым напряжениям, которым Вы и воспользовались в своем расчете. В строительстве применяется метод расчета по предельным состояниям. База у Вас есть (сопромат знаете по данному вопросу), теперь Вам надо изучать литературу по металлическим конструкциям. Суть расчета одна и та же, разница в том, что коэффициент запаса, имеющий место в сопромате, теперь разбит на множество коэффициентов надежности (по материалу, по нагрузке, по уровню ответственности здания. ) google Вам в помощь. И еще dnl. Расчет необходимо вести не по справочникам, а по актуализированной версии СНиП II-23-81* "Стальные конструкции". СП такое-то, номер не помню, есть в dnl. Будут конкретные вопросы, обращайтесь)))
Нашел два примера расчета : первый по допускаемому напряжению, второй по расчетному сопротивлению. На втором способе споткнулся. В чем моя ошибка?
Вы не понимаете суть коэффициента фи. Если вы берете один и тот же материал, допустим, сталь 3, но при этом у вас в одном случае какие-то допускаемые напряжения, а в другом - некие расчетные напряжения (расчетное сопротивление), то фи в обоих случаях будет разное. Вы пользуетесь таблицей для определения фи, но не понимаете как рассчитывали эти коэффициенты.
В общем случае фи=(сигма кр * No)/(сигма 0 * Ny),
где:
сигма кр=(пи*пи*Е)/(лямбда*лямбда), но это по Эйлеру. Для стали 3 при гибкости лямбда больше 100. При гибкости меньше 40 она вообще не учитывается (выполняется только расчет на прочность). При 40 сигма о - в данном случае (сталь 3) равно сигма текучести.
Ny - коэффициент запаса устойчивости (для стали 1,8 - 3)
N0 - основной коэффициент запаса на прочность (здесь 1,4 -1,6).
Так вот - этот N0 в таблицах взят один, а вы его произвольно меняете т.к. применяете какие-то расчетные напряжения. Откуда вы их взяли - это составителям таблицы фи (из сопроматовского учебника) было неизвестно.
Вот поэтому у вас и не получается ничего. Кстати, у вас размерности то МПа, то т/см*см. Вы уж разберитесь.
Смотрите на http://dwg.ru/dnl/9771 последнюю редакцию актуализированных СНиП. Вам нужен СВОД ПРАВИЛ СП 16.13330.2011 "СТАЛЬНЫЕ КОНСТРУКЦИИ Актуализированная редакция СНиП II-23-81*". Смотрите формулы (7) и (8). Там ясно написано как фи определять.
Offtop: Вы не могли бы рассказать - а вот зачем вам нужны эти расчеты? Вы что собственный дом конструируете?
Онлайн калькулятор расчета стойки на прочность, устойчивость и гибкость
Пример расчета деревянной стойки, подкосов на сжатие
Рассчитывается стропильная система двухскатной шиферной кровли для дома в Московской области, имеющая приблизительно следующий вид:
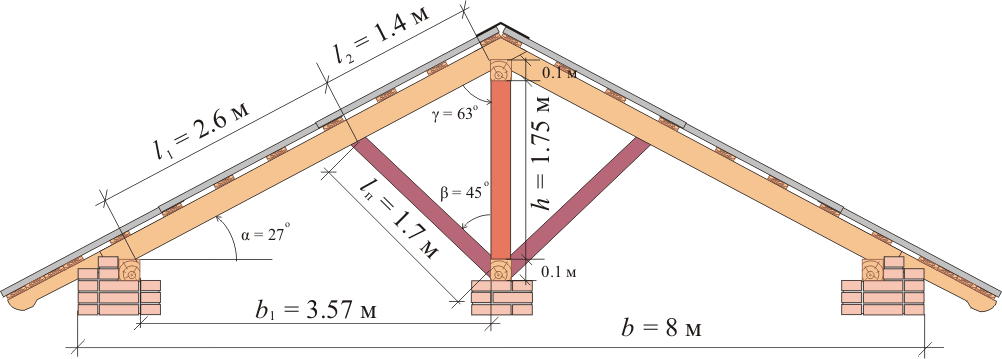
Рисунок 251.1. Данные для определения высоты опорной стойки и подкосов.
При такой стропильной схеме высота стойки составляет приблизительно h = 1.75 м (определяется через тангенс угла α, h = b1tgα - 0.05 м, где 0.05 м - приблизительная высота коньковой балки с учетом врубки). Длина подкоса приблизительно lп = 1.7 м (определяется по теореме косинусов для треугольника, так как по принципу подобия треугольников найдена одна сторона треугольника l2 = 1.4 м, то lп 2 = h 2 + l2 2 - 2hl2cosγ). Сечения стропил и обрешетки уже определены. В статье: "Двухпролетные балки" показано, как можно определить опорные реакции для стропильной ноги в данном случае являющейся двухпролетной балкой. При указанных пролетах А =1. 0556q B = 2.6978q C = 0.2464q. Для подкосов расчетной нагрузкой будет опорная реакция В, умноженная на синус угла, образованного стропилом и подкосом. Как следует из рисунка 251.1 этот угол составляет 180 - 45 - 63 = 72 о , соответственно синус этого угла составит 0.951. Тогда:
Nподкосов = 2.6978·326.1·0.951 = 836.7 кг.
Для стойки расчетной нагрузкой будет сумма опорных реакций от левой и правой стропильных ног. При определении сечения стропил мы использовали максимальное значение снеговой нагрузки:
qs лев = 180х1.25х1.2 = 270 кг/м.
Однако по принятой расчетной схеме снеговая нагрузка для противоположной стропильной ноги будет меньше:
qs прав = 180х0.75х1.2 = 162 кг/м.
q прав = qcт + qo + qш +qs прав = 3.75 + (6.25 + 16.77 +162)1.1 = 207.27 кг/м
Таким образом суммарная нагрузка на опорную стойку составит:
Nстойки = 0.2464(326.1 + 207.27) = 131.42 кг
Требуется:
Подобрать сечение опорной стойки (показана ни рисунке 251.1 оранжевым цветом) и подкосов (показаны на рисунке 251.1 фиолетовым цветом). Основные принципы расчета сжимаемых элементов изложены отдельно.
Решение:
Даже у такой, казалось бы простой задачи есть два варианта решения.
1 Вариант
Можно подобрать сечение элементов по расчетной нагрузке, однако для этого нужно знать радиус инерции сечения. Понимаю, что многие люди даже приблизительно не знают, что такое радиус инерции, ну а те кто знают, скажут, что для определения радиуса инерции нужно знать высоту и ширину сечения, а ведь именно это нам и нужно определить. Это действительно так, а еще после того, как радиус инерции известен, нужно сначала определить гибкость элемента, после этого коэффициент продольного изгиба и только потом можно определить требуемое сечение. Окончательная формула для проверки сжимаемого элемента на устойчивость достаточно проста:
σ = N/φF ≤ Rc (250.1.2)
Конечно математический аппарат позволяет решать такие задачи, однако намного проще выполнить расчет по второму варианту.
2 Вариант
Из конструктивных и технологических соображений или просто интуитивно можно сначала принять предварительно сечение элементов, а затем проверить их на устойчивость. Все равно выбор пиломатериалов по сечению сильно ограничен по сравнению с металлопрокатом и подобрать сечение так, чтобы элементы были загружены на 95-100% вряд ли получится. В данном случае, так как стропила имеют сечение 5х15 см, то сечения опорной стойки 5х5 см (если верить моей интуиции) будет вполне достаточно, а для подкосов хватит сечения 5х10 см (опять же интуиция подсказывает, но и из конструктивных соображений - для надежного соединения стропильной ноги и подкоса). Из конструктивных соображений (чтобы уменьшить количество типоразмеров при закупке делового леса) примем предварительно сечения и опорной стойки и подкосов 5х10 см.
Примечание: В принципе при столь небольших нагрузках на опорные стойки можно вообще обойтись без коньковой балки, опорная стойка может сразу подпирать стропила, но это уже вопрос удобства выполнения крыши (ведь возможно потребуется обеспечить геометрическую неизменяемость стропильной системы в плоскости, перпендикулярной показанной на рисунке 251.1, проще говоря вдоль дома), поэтому в расчетных схемах ничего менять не будем, к тому же возможные варианты стропильных систем здесь не обсуждаются.
Так как нагрузка на подкосы почти в 7 раз больше, чем нагрузка на стойки, то при принятых одинаковых сечениях стоек и подкосов и при приблизительно одинаковой расчетной длине достаточно проверить на устойчивость только подкосы.
Расчетная длина подкосов равна реальной длине lп = lo = 170 см. При ширине подкоса 5 см радиус инерции составит:
iy = (Iy/F) 1/2 = (b 2 /12) 1/2 = (5 2 /12) 1/2 = 1.44 см
теперь можно определить гибкость стропильной ноги относительно оси z:
λ = lo/iy = 170/ 1.44 = 117.78 (250.1.5)
Проверим допустимость такого значения гибкости. СНиП II-25-80 (1988) рекомендует принимать для рассчитываемых деревянных элементов такие значения гибкости, которые не превышают значения, приведенные в таблице
Таблица 1. Предельные значения гибкости (согласно СНиП II-25-80 (1988))

В нашем случае конструкцию сложно назвать фермой, согласно таблицы 1 это скорее другая сквозная конструкция и тогда предельно допустимая гибкость для нашей стойки λ = 150. Тем не менее при выполнении непрофессиональных расчетов я все-таки рекомендую использовать более строгие ограничения и принимать предельно допустимую гибкость для деревянных стоек и подкосов конструкций кровли λ ≤ 120. Полученное нами значение меньше предельно допустимого (117.78 < 120), а потому можно продолжать расчет.
так как λ > 70, то φ = А/λ 2
где А = 3000 для древесины (А = 2500 для фанеры), то
φ = 3000/117.78 2 = 0.2163
Расчетное сопротивление древесины (2 сорт) сжатию вдоль волокон - Rс = 130 кгс/см 2 (согласно СНиП II-25-80 (1988)). Площадь выбранного нами сечения F = 5х10 = 50 см 2 .
Теперь по формуле (250.1.2) мы можем определить достаточно ли выбранного нами сечения:
Как видим, такого сечения подкосов вполне достаточно и даже с запасом на возможные случайные эксцентриситеты приложения нагрузки. Можно даже использовать брус сечением 5х7 см для подкосов (но в этом случае расчет желательно выполнить с учетом случайного эксцентриситета), а уж для опорных стоек так тем более. Но из соображений удобства монтажа лучше оставить выбранное сечение.
Примечание: при значении гибкости λ < 70 коэффициент изгиба определяется по формуле:
φ = 1 - а(λ/100) 2
где а = 0.8 - для древесины, а = 1 - для фанеры
Все необходимые формальности нами соблюдены, но желательно также проверить стропильную ногу на смятие в месте контакта с подкосом.
Расчетное сопротивление древесины смятию в опорных частях конструкций, лобовых врубках и узловых примыканиях элементов (смятие поперек волокон) - Rсм90 = 30 кгс/см 2 (согласно СНиП II-25-80 (1988)).
σ = N/F ≤ Rcм90 = 836.7/50 = 16.7 < 30 кгс/см 2 (1.1)
Вот, в общем-то и весь расчет.
На этом пока все.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье "Записаться на прием к доктору"
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Для Украины - номер гривневой карты (Приватбанк) 5168 7422 4128 9630
Спасибо - добрался и сюда.
Посмотрев на приведенное описание я вижу, что на вертикально стоящую балку 10*5 см можно спокойно сверху 880кг и при этом останется запас прочности в 40% (81.34/130) - я правильно понял логику?
Не совсем. В вашем случае расчетная длина будет не 170 см, а 280 см, поэтому и нагрузка, которую выдержит стойка, будет меньше. Но если вы свяжете стойки дополнительно посредине, то уменьшите расчетную длину стоек и тогда стойки выдержат еще большую нагрузку
Поясните, пожалуйста,почему при расчете на смятие вы использовали значение расчетной нагрузки для подкосов N=879,75, тогда как выше она была расчитана как N=836,7 кг.?
Результат небрежного форматирования. Исправил.
Здравствуйте, Доктор Лом.
Если я не ошибаюсь, то у Вас опечатка в формуле
lп = h^2 + l2^2 - 2*h*l2*cos?, - lп здесь должно быть в квадрате (теорема косинусов).
Да, действительно, опечатка. Спасибо за внимательность, исправил.
Доброго времени суток, Док.
Кажется, нашёл ещё опечатку в предложении "При указанных пролетах А = 0.556q B = 2.6978q C = 0.2464q.". На самом деле A = 1.0558.
Ай молодец. Все верно, исправил.
Спасибо за наглядное объяснение! подскажите, почему не умножили расчетное сопротивление на коэф-т Мб=0.8 (высота сечения более 120см) по пункту 5.2д и табличке 9 согласно СНиП II-25-80? на результат то не особ повлияет, но все ж..
Указанный вами коэффициент Мб используется при расчете изгибаемых, внецентренно-сжатых, сжато-изгибаемых и сжатых клееных элементов прямоугольного сечения, а коэффициент Мгн - для гнутых элементов. В статье рассматривается расчет центрально сжатого прямолинейного элемента.
Тем не менее любой запас прочности, который происходит при использовании понижающего коэффициента, я приветствую.
Привет!
Скажите, для детской кровати типа чердак h 2000 -2200 мм, размер спального места 900 х 2000 мм, (ребёнок 20 -40 кг) стойки (по углам) сечением 50 х 50 мм достаточно?
Тут все не так просто. Формально такого сечения при строго вертикальной нагрузке хватит с избытком. Однако возможны технологические ослабления сечения (к стойкам нужно как-то крепить спальное место). А кроме того, в бытовых условиях нагрузки могут быть далеко не всегда вертикальными, но еще и горизонтальными. Это также нужно учитывать.
Уважаемый доктор. Предположим подкос у нас с одной стороны (т.е. система не уравновешена). Подскажите пожалуйста, при угле 45 градусов (подкоса) силы трения дерево/кирпич удержат систему в равновесии? Т.е. сила трения больше горизонтальной составляющей от приходящейся на подкос вертикальной силы. Допустим стойки, помогающей подкосу своим усилием нет. Вы где то видели официальные рекомендации какой минимальный угол можно дать подкосу, что бы система гарантированно была в равновесии?
И сразу второй вопрос.
Почему в этой схеме нет схватки?
По идее концы стропильных ног, опирающиеся на мауэрлат на стене, должны "разъезжаться".
Или их удерживает вес кирпичей с наружной стороны здания перед мауэрлатом? т.к. пролет относительно небольшой.
p.s. И по поводу вопроса выше о подкосе. Я находил в интернете цифру трения дерево о сухой кирпич - 0,6. Т.е. при 45 градусах подкос сдвинется. А каким коэффициентом трения пользуетесь Вы? есть ли официальная цифра?
Нет, таких рекомендаций я не видел и вообще считаю, что не стоит полагаться на силу трения, а следует обеспечить неподвижность элементов системы конструктивными способами.
Схватки, а точнее затяжки нет потому, что система имеет стойку. Если стойки нет, то это уже совсем другая расчетная схема и рассматривается она в других статьях.
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье "Записаться на прием к доктору" (ссылка в шапке сайта).
Читайте также:
