Расчет металлической консольной балки
Балка с любым поперечным сечением – это основополагающий элемент объемных конструкций, а деревянная балка – важный компонент зданий и сооружений. Постоянные и временные перекрытия и консоли повсеместно выполняются из брёвен, бруса или собранных в пакет досок.
Балки способны успешно воспринимать статические и динамические нагрузки: работающий человек, оборудование и имущество, интерьер и мебель уверенно размещаются на перекрытии. Предварительный расчёт прочности как оценка несущей способности призван обезопасить возводимое сооружение от поломки и придать ему необходимую жесткость – основу долговечности.
Стандартная оценка заключается в применении специализированных методик расчёта. Для этого потребуется комплексное знание механики, сопротивления материалов и других инженерных тонкостей. Гораздо проще и быстрее – провести расчет деревянной балки онлайн, с помощью отдельного инструмента в виде простого калькулятора.
Проверка балки на прогиб теперь выполняется за считанные секунды – что кардинально ускоряет работу специалиста и снижает затраты времени.
Возможности инструмента
Калькулятор прогиба деревянной балки позволяет оценить основные параметры планируемого пролётного элемента:
- размеры поперечного сечения;
- длину самой балки;
- её прогиб под планируемой нагрузкой.
Параллельно учитывается сорт древесины, что немаловажно из-за прямой зависимости между качеством пиломатериалов и механическими свойствами изделия.
Точность величины прогиба как отклонения от прямолинейности зависит от типа закрепления расчётного элемента. Жёсткая заделка обоих концов, наличие шарнирных соединений или вовсе свободный конец означают разное поведение материала балки.
Мастеру достаточно понять, как будет закрепляться каждый элемент перекрытия, измерить геометрию участка и оценить нагрузку – этого хватит для укрупнённого расчёта. Если нет точного значения приходящейся на пол массы, можно применить среднестатистические значения:
- перекрытие между этажами – до 400 кг/кв. метр;
- чердачное перекрытие – до 200 кг/кв. метр.
Порядок расчёта
Сорт пиломатериала.
Оценивается по внешнему виду и наличию дефектов, прописывается в документации по качеству на партию товара.
Для справки: сопротивление сортов древесины Приняты на основании СП 64.13330.2017 "Деревянные конструкции"
- 1-ого сорта - 9 МПа,
- 2-ого сорта - 8.34 МПа
- 3-его сорта - 5.56 МПа.
- Тип заделки концов.
Нужно определить, как будет закрепляться расчётная балка:
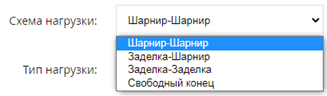
Тип нагрузки.
Расчет деревянной балки на прочность онлайн-калькулятор проводит комплексно – для чего важен характер давления.
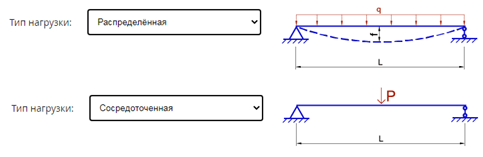
Линейные размеры сечения.
Необходимо задать размеры поперечного сечения - и определить таким образом мощность балки. Калькулятор работает с наиболее распространёнными типами сечения – прямоугольным и квадратным (при задании одинаковых ширины и высоты).
Длина балки.
На этом этапе важно ввести не полную длину – а расстояние между крайними точками, находящимися в подвешенном состоянии. Проблема заключается в распространённой ошибке: прогибу подвергается только не опирающаяся часть.
Расчет металлической консольной балки
Перед началом расчета стальной балки необходимо собрать нагрузку, действующая на металлическую балку. В зависимости от продолжительности действия нагрузки разделяют на постоянные и временные.
К постоянным нагрузкам относятся:
- собственный вес металлической балки;
- собственный вес перекрытия и т.д.;
К временным нагрузкам относятся:
- длительная нагрузка (полезная нагрузка, принимается в зависимости от назначения здания);
- кратковременная нагрузка (снеговая нагрузка, принимается в зависимости от географического расположения здания);
- особая нагрузка (сейсмическая, взрывная и т.д. В рамках данного калькулятора не учитывается);
Нагрузки на балку разделяют на два типа: расчетные и нормативные. Расчетные нагрузки применяются для расчета балки на прочность и устойчивость (1 предельное состояние). Нормативные нагрузки устанавливаются нормами и применяется для расчета балки на прогиб (2 предельное состояние). Расчетные нагрузки определяют умножением нормативной нагрузки на коэффициент нагрузки по надежности. В рамках данного калькулятора расчетная нагрузка применяется при определении прогиба балки в запас.
Нагрузки можно собрать на нашем сайте.
После того как собрали поверхностную нагрузку на перекрытие, измеряемой в кг/м2, необходимо посчитать сколько из этой поверхностной нагрузки на себя берет балка. Для этого надо поверхностную нагрузку умножить на шаг балок(так называемая грузовая полоса).
Например: Мы посчитали, что суммарная нагрузка получилась Qповерхн.= 500кг/м2, а шаг балок 2,5м. Тогда распределенная нагрузка на металлическую балку будет: Qраспр.= 500кг/м2 * 2,5м = 1250кг/м. Эта нагрузка вносится в калькулятор
2. Построение эпюр
Далее производится построение эпюры моментов, поперечной силы. Эпюра зависит от схемы нагружения балки, вида опирания балки. Строится эпюра по правилам строительной механики. Для наиболее частоиспользуемых схем нагружения и опирания существуют готовые таблицы с выведенными формулами эпюр и прогибов.
3. Расчет по прочности и прогибу
После построения эпюр производится расчет по прочности (1 предельное состояние) и прогибу (2 предельное состояние). Для того, чтобы подобрать балку по прочности, необходимо найти требуемый момент инерции Wтр и из таблицы сортамента выбрать подходящий металлопрофиль. Вертикальный предельный прогиб fult принимается по таблице 19 из СНиП 2.01.07-85* (Нагрузки и воздействия). Пункт2.а в зависимости от пролета. Например предельный прогиб fult=L/200 при пролете L=6м. означает, что калькулятор подберет сечение прокатного профиля (двутавра, швеллера или двух швеллеров в коробку), предельный прогиб которого не будет превышать fult=6м/200=0,03м=30мм. Для подбора металлопрофиля по прогибу находят требуемый момент инерции Iтр, который получен из формулы нахождения предельного прогиба. И также из таблицы сортамента подбирают подходящий металлопрофиль.
4. Подбор металлической балки из таблицы сортамента
Из двух результатов подбора (1 и 2 предельное состояние) выбирается металлопрофиль с большим номером сечения.
Чтобы посчитать сечение деревянной балки - необходимо собрать нагрузку, действующая на балку. В зависимости от длительности действия нагрузки разделяют на постоянные и временные.
- собственный вес деревянной балки;
- собственный вес перекрытия, чердачного перекрытия и т.д.;
Например: Мы посчитали, что суммарная нагрузка получилась Qповерхн.= 400кг/м2, а шаг балок 0,6м. Тогда распределенная нагрузка на деревянную балку будет: Qраспр.= 400кг/м2 * 0,6м = 240кг/м. Эта нагрузка вносится в калькулятор
2. Выбор предельного прогиба
В зависимости от назначения балки и ее пролета задаем вертикальный предельный прогиб по таблице 19 из СНиП 2.01.07-85* (Нагрузки и воздействия) Пункт2.а. Смысл вертикального прогиба заключается в следующем: например, прогиб l/250 означает, что для балки длинной 4м предельный вертикальны прогиб равен fult = 4м / 250 = 0,016м = 16мм в месте максимального прогиба для балки. Для балки на двух опорах загруженной равномерно или с сосредоточенной нагрузкой посередине балки - максимальный прогиб будет посередине пролета. Для консольной балки максимальный прогиб - на свободном конце балки.
3. Задание ширины искомого сечения балки.
В зависимости от конструктивных требований задаем ширину сечения балки. Расчет деревянной балки сводится к тому, что необходимо подобрать требуемую высоту hтр сечения деревянной балки, которое способно выдержать заданную нагрузку и не превысить заданный предельный прогиб.
Алгоритм расчета деревянной балки, используемый в данном калькуляторе
По заданной нагрузке и пролету производится построение эпюры моментов и поперечной силы. Эпюра поперечной силы находится для информации (чтобы знать какая нагрузка давит на опоры балки) и в расчете не используется. Эпюра зависит от схемы нагружения балки, вида опирания балки. Строится эпюра по правилам строительной механики. Для наиболее частоиспользуемых схем нагружения и опирания существуют готовые таблицы с выведенными формулами эпюр и прогибов.
2. Расчет по прочности и прогибу
После построения эпюр производится расчет по прочности (1 предельное состояние) и прогибу (2 предельное состояние). Для того, чтобы подобрать балку по прочности, необходимо найти требуемый момент инерции Wтр и hтр и из таблицы рекомендуемого сортамента выбрать подходящее сечение высотой равное hтр деревянной балки по ширине сечения (b) и по Wтр. Следует отметить, что калькулятор подбирает именно по Wтр, нахождение hтр сделано для наглядности, чтобы видеть какая высота сечения должна быть. Для подбора деревянной балки по прогибу находят требуемый момент инерции Iтр, который получен из формулы нахождения предельного прогиба. И также из таблицы сортамента пиломатериалов подбирают подходящее сечение.
3. Подбор деревянной балки из таблицы сортамента пиломатериалов по ГОСТ 244454-80
Из двух результатов подбора (1 и 2 предельное состояние) выбирается сечение с большей выстой сечения.
Однопролетные строительные конструкции могут опираться на что угодно и закреплены при этом могут быть по-разному. Металлические и железобетонные перемычки, плиты перекрытия как правило укладываются на цементно-песчаный раствор, деревянные балки перекрытия могут быть прибиты гвоздями или прикручены шурупами или просто оперты на стены, элементы железобетонного каркаса обычно соединяются с помощью электросварки и бетонирования, металлические конструкции могут быть соединены при помощи сварки, болтов или заклепок. Но строительная механика таких способов опирания и закрепления не знает, а предлагает нам для расчетов совсем другие варианты опор, из которых самые распространенные - это шарнирное опирание и жесткое защемление на опоре. А ведь при расчете строительных конструкций одна их первейших задач - это определение опорных связей, проще говоря, выбор опор. Понять, почему это так важно, поможет следующий пример:
Расчетые схемы наклонных балок
Расчет наклонных балок вообще и стропил в частности имеет одну интересную особенность. Одни авторы утверждают, что в наслонных стропилах нормальных напряжений растяжения или сжатия при действии вертикальной нагрузки не возникает. Другие - что эти напряжения хоть и возникают, но крайне незначительны и их значением для упрощения расчетов можно пренебречь. Третьи - что учитывать нормальные напряжения при расчете наклонных балок все-таки нужно.
Из-за чего же возникает такое разнообразие мнений и самое главное: как поступить простому человеку при расчете стропильной системы? Давайте попробуем разобраться.
Общий случай расчета балки на шарнирных опорах при действии нескольких сосредоточенных нагрузок
Первый этап расчета однопролетной балки на шарнирных опорах - определение максимальных изгибающих моментов, поперечных сил, углов поворота и прогибов - большой сложности не представляет, если к балке приложена одна сосредоточенная нагрузка. Все необходимые формулы для этого частного случая уже имеются, достаточно лишь подставить в эти формулы свои значения.
Тем не менее очень часто балка бывает загружена несколькими сосредоточенными нагрузками. Если эти нагрузки равны и приложены симметрично, то наиболее простой способ расчета такой балки - перевести сосредоточенные нагрузки в эквивалентную равномерно распределенную.
Однако в общем случае сосредоточенные нагрузки к однопролетной балке на шарнирных опорах могут быть приложены не симметрично, да и значения сосредоточенных нагрузок могут быть разными. И в этом общем случае для получения точных результатов отделаться малой кровью не получится, необходимо выполнять полный расчет по общему протоколу.
Расчет балки. Общие положения
Расчет любой балки состоит из двух основных этапов. Первый этап - определение максимальных напряжений, действующих в поперечных сечениях балки. Второй этап - выбор материала балки и определение характеристик сечения, удовлетворяющих условиям, определенным на первом этапе.
Таким образом на первом этапе расчетов знать материал, из которого будет изготавливаться балка, расчетное сопротивление и прочие характеристики материала вовсе не обязательно. В связи с этим расчет балки на первом этапе - задача строительной механики, а второй этап - удел теории сопротивления материалов.
А теперь рассмотрим каждый из этих этапов более подробно.
К расчету балок на упругом основании
В малоэтажном строительстве, как впрочем и в любом другом, балки на упругом основании встречаются намного чаще, чем это можно подумать. По той причине, что любой ленточный фундамент, а иногда и плитный фундамент можно рассматривать как балку на упругом основании.
И если с расчетом балки - ленточного фундамента проблем практически не возникает по той простой причине, что нагрузка на ленточный фундамент как правило равномерно распределенная, а значит и фундамент ведет себя, как абсолютно жесткая балка, дополнительных расчетов не требующая. То при рассмотрении участка плитного фундамента как балки или ленточного фундамента с неравномерно приложенной нагрузкой могут возникнуть некоторые проблемы.
Расчет балки из разнородных материалов
Балки из разнородных материалов встречаются в малоэтажном строительстве достаточно редко. Тем не менее, все-таки встречаются и потому следует понимать, как подобные балки рассчитываются.
Например, если к деревянной балке перекрытия прикрепить снизу (или сверху) металлическую полосу, то это и будет балка из разнородных материалов. Расчет железобетонных балок, которые также могут рассматриваться как балки из разнородных материалов, в данной статье не рассматривается, так как это отдельная большая тема.
Примечание: Как именно будет осуществляться крепление, чтобы обеспечить совместную работу материалов, в данной статье не рассматривается. Основное внимание будет уделено принципам расчета подобной балки. И металлическую полосу лучше крепить снизу, чтобы металл работал на растяжение, а не на сжатие.
Виды балок
С тех пор как наши предки вышли из пещер и занялись возведением жилья из подручных материалов, одной из самых важных проблем строительства остается вопрос изготовления перекрытия, проще говоря, крова над головой. Для перекрытия небольших пролетов (1-6 м) издревле использовались деревянные балки - бревна. Для перекрытия бóльших пролетов изготавливались достаточно сложные арочные плоские или пространственные конструкции из камня, кирпича и даже бетона, имитирующие небесный свод.
Нужно отдать должное нашим предшественникам, не имея ни малейших представлений о теории сопротивления материалов, строительной механике и прочих мудреных дисциплинах, не пользуясь электроинструментом, автомобилями, одним словом обладая минимальной технической базой, они уже строили храмы и святилища и мосты с пролетами в несколько десятков метров, причем некоторые из них сохранились до наших дней.
Расчет балок переменного сечения
В данной статье рассматриваются принципы расчета балок не равного сопротивления изгибающему моменту, т.е. таких балок прямоугольного сечения, один из геометрических параметров поперечного сечения которых уменьшается обратно пропорционально действующему изгибающему моменту. Основные принципы расчета таких балок такие же, как и балок равного сопротивления изгибающему моменту, но есть некоторые особенности.
1. Расчет балок прямоугольного сечения, изменение одного из геометрических параметров сечения которой носит обратный характер, может выполняться на основании следующих предположений:
Расчет балок равного сопротивления изгибающему моменту
Расчет на прочность балок равного сопротивления изгибающему моменту, другими словами балок, нормальные напряжения в поперечных сечениях которых постоянны, мало чем отличается от расчета балок постоянного сечения, так как требования по прочности остаются неизменными - напряжения в максимально нагруженном сечении не должны превышать максимально допустимых. А вот определение деформаций балок равного сопротивления изгибающему моменту имеет свои особенности.
Вопрос по креплению консоли с подпором
19-07-2015: Bespalovs
Встал следующий вопрос. Консоль имеет вылет 1600 мм. Распределенная нагрузка 2.7 кгс см.
В приведенном виде, по моему мнению, это конструкция, состоящая из стержней, соединенных шарнирами.
Необходимо определить наиболее экономичный способ реализации.(тип металлической балки – сечение, тип подкоса и вариант его установки (снизу или сверху)
Балки переменного сечения
В строительстве нередко используются элементы конструкций, имеющие ярко выраженное переменное по длине сечение. Например любую железобетонную балку, в растягиваемой зоне которой возникают трещины, можно рассматривать как балку переменного сечения. В связи с этим расчет балок переменного сечения представляет определенный интерес.
Очень часто при расчете строительных конструкций рассматриваются элементы, имеющие постоянное по длине поперечное сечение. Именно такое сечение как правило рассматривается при определении прочности и прогибов изгибаемых элементов. Чаще всего в качестве изгибаемых элементов рассматриваются прямолинейные стержни - балки.
Консольная балка с загруженными консолями
На первый взгляд такой вариант загружения балки - симметрично загруженные консоли и отсутствие нагрузки посредине - может показаться достаточно редким и потому необходимость расчета такой консольной балки - сомнительной. Но не будем торопиться с выводами и определим, в чем особенность работы балки с симметрично загруженными консолями.
Для простоты рассмотрим балку, имеющую равные по длине консоли k, к которым приложена одинаковая по значению симметричная нагрузка. Например, имеется балка пролетом l, с равными консолями k, на концах которых приложена сосредоточенная нагрузка Q (рис. 384.1. а)):
К расчету консольных балок
Консольная балка - достаточно сложная балка, не смотря на кажущуюся простоту. Например, есть доска длиной 3 м, доска лежит на некоем основании шириной 1 м, при этом свесы доски с каждой из сторон составляют 1 м. На доску действует равномерно распределенная нагрузка 100 кг/м. И тут возникает вопрос: как рассчитать такую балку?
1 вариант
Вроде бы у балки одна опора и повороту поперечных сечений она не мешает и получается, что эту опору можно рассматривать как шарнирную. Вот только такого понятия, как ширина опоры, во всяком случае на первом этапе расчета, при рассмотрении расчетных схем балок не существует.
Получается, что нашу доску мы можем рассматривать как балку с одной опорой и 2 консолями. Если ширину опоры не учитывать, длина консолей будет k = 1 м, а максимальный момент, действующий на опоре, будет составлять:
Метод нулевых моментных точек
Использование метода нулевых моментных точек позволяет значительно упростить решение ряда задач строительной механики, связанных с расчетом статически неопределимых конструкций.
Суть метода нулевых моментных точек рассмотрим на примере однопролетной балки с жестким защемлением на одной их опор.
Расчет балки на действие распределенной и сосредоточенной нагрузок
Когда на балку действует несколько нагрузок: равномерно распределенная по всей длине и сосредоточенная посередине длины балки, то для упрощения расчетов сосредоточенную нагрузку можно перевести в эквивалентную равномерно распределенную.
Но в некоторых случаях, например при расчете плиты перекрытия на которую будут монтироваться перегородки, сосредоточенная нагрузка может быть приложена не посередине длины плиты и для определения максимального изгибающего момента требуется выполнить полный расчет. Этим мы сейчас и займемся.
Формулы для расчета балки с консолями на действие равномерно распределенной нагрузки
Если однопролетная балка с шарнирными опорами имеет консоли, разные по длине, то рассчитать такую балку по простым общеизвестным формулам из справочника не получится. Даже если на такую балку действует равномерно распределенная нагрузка.
Все из-за того, что формулы для определения опорных реакций, моментов, прогибов получаются достаточно громоздкими. Тем не менее ничего сложного в таких расчетах нет.
Шарнирно-опертая балка с трапециевидной распределенной нагрузкой
05.02.2016 Анна
Добрый день, Доктор
Со сложением опорных реакций, моментов и эпюры Q проблем конечно не возникло.
Меня очень интересует формула для определения прогибов и угла поворота для трапециевидной нагрузки вида 2.1+2.5, когда слева, скажем нагрузка q1, а справа q2. Или нагрузка для схемы 2.1 - q1, а для схемы 2.5 q2.
Никак не совладаю с формулой для определения максимального прогиба и прогиба вообще и угла поворота.
Читайте также:
