Расчет изгиба листового металла
При выполнении расчетов стенок емкостей, стенок конструкций или различных покрытий возникает задача определения напряжений и прогибов. Хочется получить быстрый ответ на простые вопросы — .
. на сколько и как выгнется пластина под нагрузкой, и не разрушится ли она? Теория предлагает по заданной известной функции нагрузки найти функцию прогибов. Для этого нужно решить неоднородное бигармоническое дифференциальное уравнение четвертого порядка в частных производных. От одного прочтения предыдущего предложения, я думаю, многим читателям стало грустно и тоскливо. А если добавить, что для практической реализации одного из методов предстоит решить систему из 15-и уравнений и найти 15 неизвестных, то большинство на этом просто прекратят чтение и потеряют всякий интерес к теме, либо продолжат поиск программ, выполняющих автоматически подобные расчеты. Эти программы, выполняющие расчет прогиба пластин, чаще всего реализуют приближенные численные методы конечных элементов и конечных разностей и стоят приличных денег.
Но есть и другой путь… (Как известно, выходов всегда не меньше двух. ) Эта дорога старая, заросшая лесом новых теорий, но не до конца забытая!
Этот путь является достаточно узким и индивидуальным для различных форм пластин, способов закрепления контуров и относительных величин прогибов. Для каждой расчетной схемы – свои таблицы коэффициентов к расчетным формулам! Расчет прогиба пластины по старым методикам прост – это несомненный плюс, но не универсален – это существенный минус.
Цель данной статьи – рассказать, как наши деды — инженеры прошлого века — решали такие практические вопросы, и показать простой пример модернизированного расчета в Excel задачи об изгибе пластины для одного из наиболее распространенных случаев в практике.
Из-за отсутствия каких-либо машин для выполнения рутинных сложных расчетов (кроме светлой головы, листка бумаги, карандаша, таблиц функций и логарифмической линейки ничего не было) ученые в начале и в середине 20-ого века стремились вооружить простого инженера короткими и понятными алгоритмами, «привязанными» к рассчитанным в НИИ номограммам и таблицам. Такой подход обеспечивал значительное упрощение и ускорение работы инженеров, хотя и не давал им полного понимания теории.
Расчет прогиба пластины изучается в общей теории оболочек, которая является сложным самостоятельным разделом механики, давно выделившимся из недр классического сопромата.
Теория тонких пластин распространяется на листы и плиты, у которых толщина h менее 20% от наименьшего габаритного размера в плане a .
Тонкие пластины делят на 3 класса в зависимости от величины максимального прогиба w :
гибкие — 0,25 h < w
абсолютно гибкие — w >5 h
Попадание конкретной пластины в тот или иной класс, как видите, зависит от прогиба, а значит — от величины нагрузки. Важно отметить, что одна и та же пластина при разных нагрузках может быть отнесена к разным классам, и расчет её будет производиться по различным формулам.
Далее в примере рассматривается тонкая жесткая пластина.
Расчет в Excel прогиба пластины. Пример.
Прямоугольная пластина из изотропного материала (Сталь Ст3) жестко закреплена по всему контуру. В перпендикулярном направлении к плоскости пластины приложена равномерно распределенная по всей площади нагрузка.
Требуется вычислить наибольший прогиб пластины от действия нагрузки и найти максимальные возникающие в теле листа напряжения.

Исходные данные:
Первые три параметра являются справочными характеристиками свойств материала пластины.
1. Предел текучести для пластичных материалов или прочности для хрупких материалов [σ] в Н/мм 2 записываем
в ячейку D3: 245
Этот параметр не участвует в расчетах и нужен лишь для сравнения с полученными в результате расчета напряжениями. Правильнее вместо него использовать допускаемые напряжения материала с учетом всех запасов для конкретного случая применения.
2. Модуль упругости или модуль Юнга E в Н/мм 2 заносим
в D4: 210000
3. Коэффициент Пуассона μ вписываем
в D5: 0,28
В примечаниях к ячейкам D4 и D5 приведены значения модулей упругости и коэффициентов Пуассона для некоторых материалов.
4.,5.,6. Далее вводим в таблицу размеры пластины h , a и b в мм
в ячейку D6: 5,0
в D7: 500
в D8: 1000
В примечаниях к ячейкам D6, D7 и D8 записаны ограничения, которые должны соблюдаться. В случае их нарушения цифры окрашиваются инверсным белым цветом, а поле ячейки – красным, сообщая пользователю об ошибке ввода данных.
7. Значение распределенной равномерно по всей площади нагрузки q в Н/мм 2 вносим
в D9: 0,016

Прошу УВАЖАЮЩИХ труд автора скачать файл ПОСЛЕ ПОДПИСКИ на анонсы статей в окне, расположенном вверху страницы или сразу после статьи.
Ссылка на скачивание файла с программой: raschet-progiba-plastiny-NEW (xlsx 174KB).
Результаты расчета:
8. Цилиндрическую жесткость пластины D в Н*мм (аналог EI – линейной жесткости для стержней) вычисляем
в ячейке D11: D =( E * h 3 )/(12*(1- μ 2 )=2373589
9.,11. Безразмерные коэффициенты k1 и k2 , зависящие от формы и размеров пластины, а также от способов закрепления контурных сторон, можно найти в таблицах старых справочников (Тимошенко С.П., Войновский-Кригер С. Пластины и оболочки; Вайнберг Д.В, Вайнберг Е.Д. Расчет пластин). Правда, k2 зависит еще и от μ , а в таблицах приведены значения только для стали μ ≈0,3 и бетона μ ≈1/6, но, проанализировав ряд таблиц, можно увидеть, что эта зависимость не очень значительная…

Выполнив аппроксимацию в Excel табличных данных, получим аналитические выражения для расчетов коэффициентов
в ячейке D12: при 0,5< a / b
k1 =0,16747*( a / b ) 6 -0,766*( a / b ) 5 +1,4455*( a / b ) 4 -1,4342*( a / b ) 3 +0,78433*( a / b ) 2 -0,22506*( a / b )+0,029239=0,0254
k1 =-0,00012*( a / b )+0,0026=0,0254

k2 =0,71922*( a / b ) 6 -3,1489*( a / b ) 5 +5,6353*( a / b ) 4 -5,1372*( a / b ) 3 +2,3658*(a/b) 2 -0,50294*( a / b )+0,12003=0,0829
k1 =-0,0008*( a / b )+0,0833=0,0829

Точность аппроксимации очень и очень высокая. Об этом можно судить как по абсолютным Δабс и относительным Δотн погрешностям, так и по величине достоверности R 2 .
10. Максимальный прогиб пластины w в мм будет в рассматриваемой схеме в центре пластины в точке O; вычисляем его
в ячейке D13: w = k1 * q * a 4 / D =1,07
Расчет прогиба в MS Excel выполнен. Величина прогиба не превышает четверти толщины листа, следовательно применение использованных формул правомерно.
12. Наибольшие моменты на единицу длины сечения пластины Mmax возникают в рассматриваемой схеме по серединам больших сторон контура в точках A и A’. Вычисляем их в Н*мм/мм
в ячейке D15: Mmax = k2 * q * a 2 =332
13. Наибольшие напряжения в пластине σmax в точках действия максимального момента вычисляем в Н/мм 2
в ячейке D16: σmax =6* Mmax / h 2 =80
Напряжения не превышают предела текучести. Деформации листа являются упругими, после снятия нагрузки пластина вернется в исходное плоское состояние.
Заключение.
По предложенной программе в Excel можно выполнять расчет прогиба тонкой жесткой прямоугольной пластины из любого изотропного материала – стекла, пластмассы, бетона, любого металла при жестком закреплении контура.
Прогиб вычисляется точно для любых материалов. Напряжения рассчитываются точно только для стали. Чем значительней коэффициент Пуассона материала отличается от коэффициента Пуассона стали, тем больше будет ошибка в определении действующих напряжений.
Так как способов закрепления контура пластины, видов форм пластины, сочетаний нагрузок — очень много, то задача расчета прогибов при рассмотренном подходе к решению распадается на сотни индивидуальных задач, в которых значения коэффициентов k1 и k2 также индивидуальны!
В продолжение темы «Расчет прогиба пластины» может быть в одной из будущих публикаций попробую рассмотреть более универсальный подход – метод конечных разностей с использованием MS Excel.
P. S. (27.03.2022)
В файл с расчетами добавлены вычисления максимальных прогибов и напряжений по двум схемам для круглых пластин.
Гибка листового металла - методы и советы по проектированию [часть 1]

Гибка - одна из наиболее распространенных операций по изготовлению листового металла. Этот метод, также известен как прессование, отбортовка, гибка штампа, фальцовка и окантовка, этот метод используется для деформации материала до угловой формы.
Это достигается за счет приложения силы к заготовке. Сила должна превышать предел текучести материала для достижения пластической деформации. Только так можно получить стойкий результат в виде изгиба.
Какие методы гибки наиболее распространены? Как пружинистость влияет на изгиб? Что такое k-фактор? Как рассчитать допуск на изгиб?
Все эти вопросы обсуждаются в этом посте вместе с некоторыми советами по гибке.
Методы гибки:
Существует довольно много различных методов гибки. У каждого есть свои преимущества. Обычно возникает дилемма между стремлением к точности или простоте, в то время как последняя находит все большее применение. Более простые методы более гибкие и, что наиболее важно, для получения результата требуется меньше различных инструментов.
V-образный изгиб:
V-образная гибка является наиболее распространенным методом гибки с использованием пуансона и штампа. Она имеет три подгруппы - гибка на основе или нижняя гибка, «свободная» или «воздушная» гибка и чеканка. На воздушную гибку и гибку на основе приходится около 90% всех операций гибки.
Приведенная ниже таблица поможет вам определить минимальную длину фланца b (мм) и внутренний радиус ir (мм) в зависимости от толщины материала t (мм). Вы также можете увидеть ширину матрицы V (мм), которая необходима для таких характеристик. Для каждой операции нужен определенный тоннаж на метр. Это также показано в таблице. Вы можете видеть, что более толстые материалы и меньшие внутренние радиусы требуют большей силы или тоннажа. Выделенные параметры являются рекомендуемыми спецификациями для гибки металла.
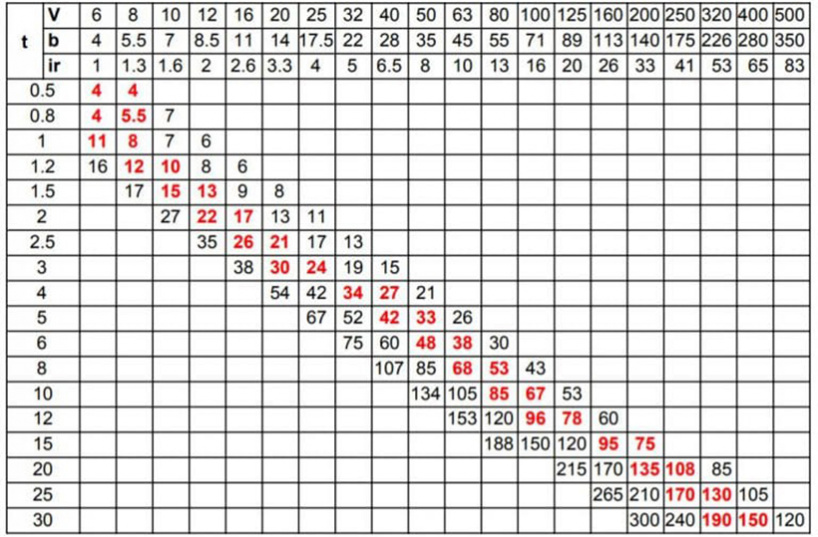
График силы изгиба
Допустим, у меня есть лист толщиной 2 мм, и я хочу его согнуть. Для простоты я также использую внутренний радиус 2 мм. Теперь я вижу, что минимальная длина фланца для такого изгиба составляет 8,5 мм, поэтому я должен учитывать это при проектировании. Требуемая ширина матрицы составляет 12 мм, а тоннаж на метр - 22. Самая низкая общая производительность стенда составляет около 100 тонн. Линия гибки моей заготовки составляет 3 м, поэтому общая необходимая сила составляет 3 * 22 = 66 тонн. Таким образом, даже простой верстак, с достаточным количеством места, чтобы согнуть 3-метровые листы, подойдет.
Тем не менее, нужно помнить об одном. Эта таблица применима к конструкционным сталям с пределом текучести около 400 МПа. Если вы хотите согнуть алюминий , значение тоннажа можно разделить на 2, так как для этого требуется меньше усилий. С нержавеющей сталью происходит обратное - требуемое усилие в 1,7 раза больше, чем указано в этой таблице.
Нижнее прессование:
При нижнем прессовании, пуансон прижимает металлический лист к поверхности матрицы, поэтому угол матрицы определяет конечный угол заготовки. Внутренний радиус скошенного листа зависит от радиуса матрицы.
По мере сжатия внутренней линии требуется все большее усилие для дальнейшего манипулирования ею. Нижнее прессование позволяет приложить это усилие, так как конечный угол задан заранее. Возможность приложить большее усилие уменьшает пружинящий эффект и обеспечивает хорошую точность.
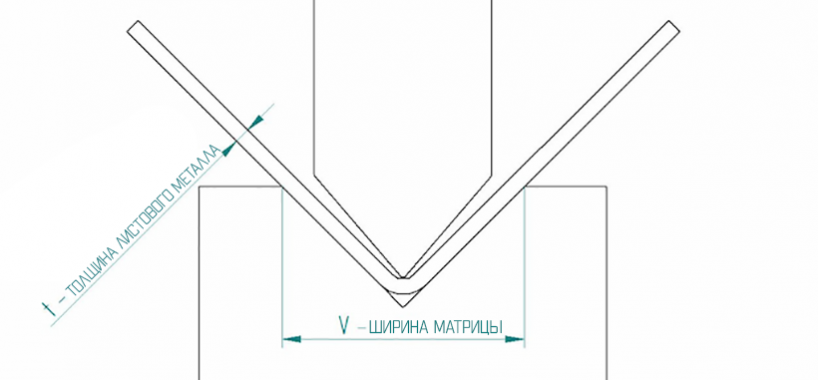
Разница углов учитывает эффект пружинящего отката
При нижнем прессовании важным этапом является расчет отверстия V-образной матрицы.
| Ширина проема V (мм) | ||||
| Метод / Толщина (мм) | 0,5…2,6 | 2,7…8 | 8,1…10 | Более 10 |
| Нижнее прессование | 6т | 8т | 10т | 12т |
| Свободная гибка | 12. 15т | |||
| Чеканка | 5т | |||
Экспериментально доказано, что внутренний радиус составляет около 1/6 ширины проема, что означает, что уравнение выглядит следующим образом: ir = V/6.
Воздушная гибка:
Частичная гибка, или воздушная гибка, получила свое название от того факта, что обрабатываемая деталь фактически не касается деталей инструмента полностью. При частичном гибе заготовка опирается на 2 точки, и пуансон толкает изгиб. По-прежнему обычно выполняется на листогибочном прессе, но при этом нет фактической необходимости в боковом штампе.
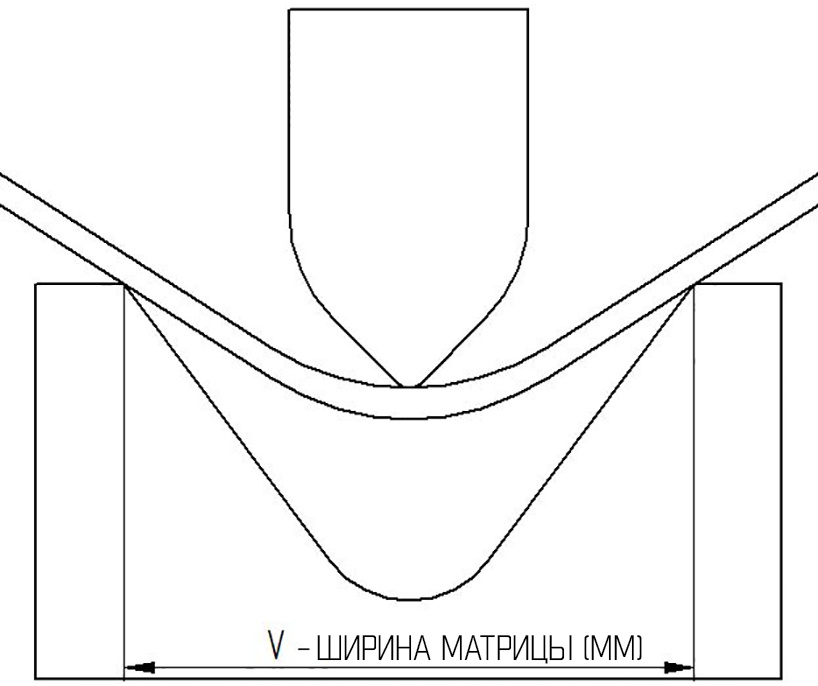
Воздушная гибка дает большую гибкость. Допустим, у вас есть матрица и пуансон на 90°. С помощью этого метода вы можете получить результат от 90 до 180 градусов. Хотя этот метод менее точен, чем штамповка или чеканка, в его простоте и заключается его прелесть. В случае, если нагрузка ослабнет, и упругая отдача материала приведет к неправильному углу, его легко отрегулировать, просто приложив еще немного давления.
Конечно, это результат меньшей точности по сравнению с нижним прессованием. В то же время большим преимуществом частичной гибки является то, что для гибки под другим углом не требуется переналадка инструмента.
Чеканка:
Раньше чеканка монет была гораздо более распространена. Это был практически единственный способ получить точные результаты. Сегодня техника настолько хорошо контролируема и точна, что такие методы больше не используются.
Чеканка при гибке дает точные результаты. Например, если вы хотите получить угол в 45 градусов, вам понадобятся пуансон и матрица с точно таким же углом. Не о чем беспокоиться.
Почему? Потому что штамп проникает в лист, вдавливая углубление в заготовку. Это, наряду с большим усилием (примерно в 5-8 раз больше, чем при частичной гибке), гарантирует высокую точность. Проникающий эффект также обеспечивает очень маленький внутренний радиус изгиба.
U-образная гибка:
U-образная гибка в принципе очень похожа на V-образную. Есть матрица и пуансон, на этот раз они имеют U-образную форму, что приводит к аналогичному изгибу. Это очень простой способ, например, гибки стальных U-образных каналов, но он не так распространен, поскольку такие профили также можно производить с использованием других, более гибких методов.
Ступенчатая гибка:
Ступенчатая гибка - это, по сути, многократная V-гибка. Этот метод, также называемый гибовкой вразбежку, использует множество последовательных V-образных изгибов для получения большого радиуса заготовки. Окончательное качество зависит от количества изгибов и шага между ними. Чем их больше, тем более гладким будет результат.
Валковая гибка:
Валковая гибка используется для изготовления труб или конусов различной формы. При необходимости может также использоваться для изгибов с большим радиусом. В зависимости от мощности машины и количества рулонов можно выполнять один или несколько изгибов одновременно.
При этом используются два приводных ролика и третий регулируемый. Этот ролик движется за счет сил трения. Если деталь необходимо согнуть с обоих концов, а также в средней части, требуется дополнительная операция. Это делается на гидравлическом прессе или листогибочном станке. В противном случае края детали получатся плоскими.
Гибка с вытеснением:
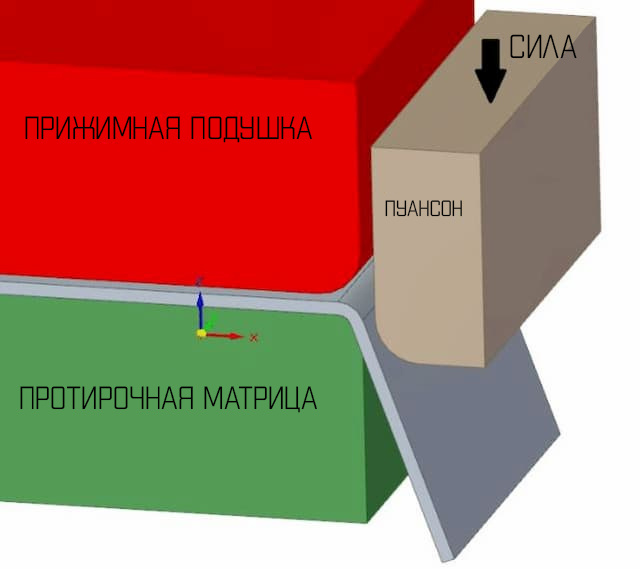
При гибке с вытеснением листовой металл зажимается между прижимной подушкой и штампом для протирания. Форма штампа для протирки, расположенного внизу, определяет угол получаемого изгиба. После того, как металлический лист был надежно зажат, перфоратор опускается на свисающий конец металлического листа, заставляя его соответствовать углу протирочной матрицы. Конечным результатом обычно является чеканка металлического листа вокруг протирочного штампа.
Ротационная гибка:
Другой способ - ротационная гибка, она имеет большое преимущество перед гибкой вытеснением или V-образной гибкой - она не царапает поверхность материала. На самом деле, существуют специальные полимерные инструменты, позволяющие избежать каких-либо следов от инструмента, не говоря уже о царапинах. Ротационные гибочные станки также могут сгибать более острые углы, чем 90 градусов. Это очень помогает с общими углами.
Наиболее распространенный метод - с двумя валками, но есть также варианты с одним валком. Этот метод также подходит для производства U-образных каналов с близко расположенными фланцами, так как он более гибкий, чем другие методы.
Возврат при сгибе:
При сгибании заготовка естественным образом немного отскакивает после подъема груза. Следовательно, эту величину необходимо компенсировать при изгибе. Заготовка изгибается под необходимым углом, поэтому после упругого возврата она принимает желаемую форму.
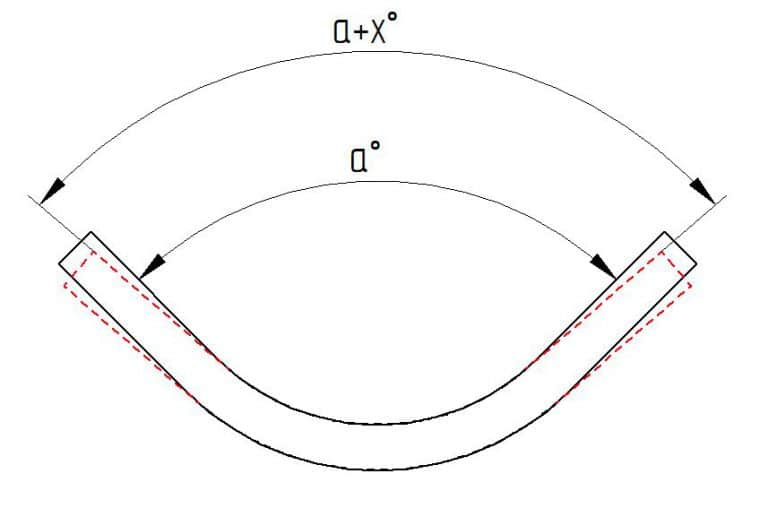
Еще один момент, о котором следует помнить, - радиус изгиба. Чем больше внутренний радиус, тем больше пружинящей эффект. Острый пуансон дает маленький радиус и снимает пружинящий эффект.
Почему происходит пружинение? При сгибании деталей сгиб делится на два слоя разделяющей их линией - нейтральной линией. С каждой стороны происходят разные физические процессы. «Внутри» материал сжимается, «снаружи» - вытягивается. Каждый тип металла имеет разные значения нагрузок, которые они могут воспринимать при сжатии или растяжении. И прочность материала на сжатие намного превосходит прочность на разрыв.
В результате, на внутренней стороне труднее достичь постоянной деформации. Это означает, что сжатый слой не деформируется окончательно и пытается восстановить свою прежнюю форму после снятия нагрузки.
Допуск на изгиб
Если вы проектируете гнутые детали из листового металла в программе CAD, которая имеет специальную среду для работы с листовым металлом, используйте ее. Она существует не просто так. При выполнении изгибов она учитывает спецификации материалов. Вся эта информация необходима при изготовлении плоского шаблона для лазерной резки.
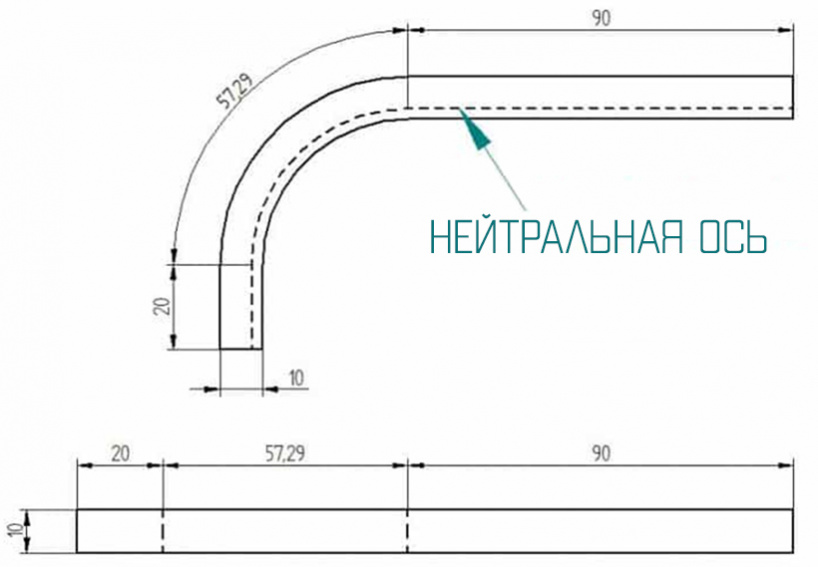
Длина дуги нейтральной оси должна использоваться для расчета развертки.
Если вам понравилась статья, то ставьте лайк, делитесь ею со своими друзьями и оставляйте комментарии!
Гибка листового металла - методы и советы по проектированию [часть 2]

Если вы сами создаете чертежи, вам нужно знать следующее. Процесс гибки удлиняет материал. Это означает, что нейтральная линия или ось, о которой мы говорили в предыдущей статье, на самом деле находится не посередине материала. Но плоская деталь должна быть сформирована в соответствии с нейтральной линией. И для нахождения ее положения требуется коэффициент k.
Коэффициент K - это эмпирическая константа, то есть его значение было определено в результате испытаний. Он варьируется в зависимости от материала, его толщины, радиуса изгиба и метода гибки. По сути, коэффициент k смещает нейтральную линию, чтобы обеспечить плоский рисунок, отражающий реальность. Используя его, вы получаете допуск на изгиб, который, по сути, является длиной изогнутой нейтральной оси.
Первую часть данной статьи вы можете найти в нашем блоге по ссылке. Примечание: данная статья является переводом.
Формула коэффициента K:
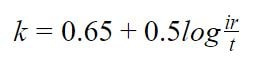
Формулы припусков на изгиб:
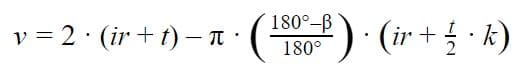
Для изгибов от 90 до 165 градусов формула имеет вид:
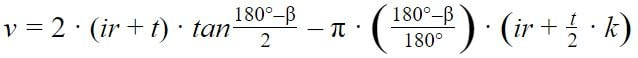
Для изгибов более 165° нет необходимости рассчитывать припуски на изгиб, так как нейтральная ось остается практически посередине детали.
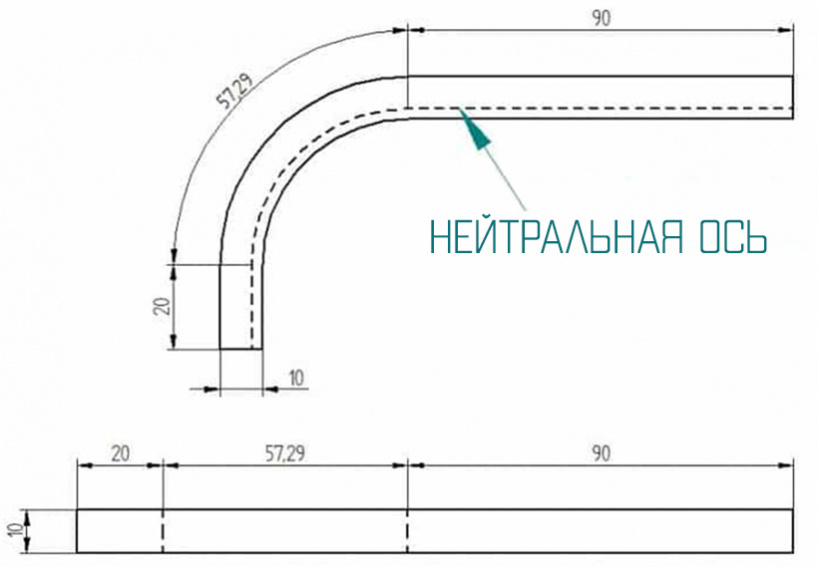
Для расчета плоской детали необходимо использовать длину дуги нейтральной оси
Расчет допуска на изгиб:
Допустим, у вас есть деталь, похожая на ту, что на изображении выше - у нее прямая ножка 20 мм и другая 70 мм. Угол изгиба составляет 90°, толщина листа - 5 мм, а внутренний радиус - 6 мм. Мы хотим узнать конечную длину детали. Во-первых, мы должны начать с коэффициента k:
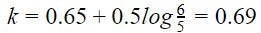
Другой способ определения коэффициента k - следовать "правилу большого пальца". Просто выберите коэффициент k в соответствии с вашим материалом из приведенной ниже таблицы. Это дает достаточно точные результаты для большинства случаев.
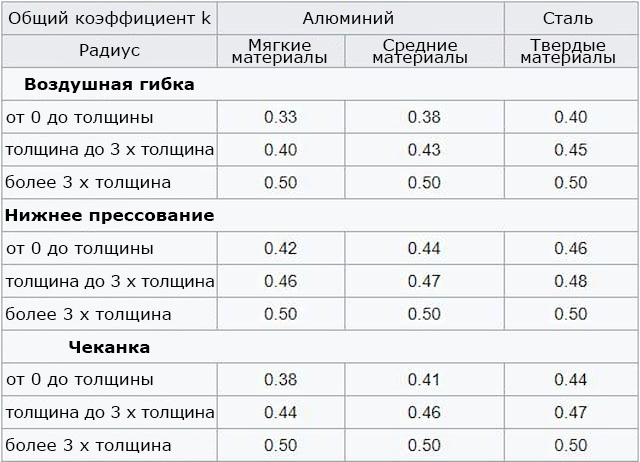
Теперь мы можем перейти к припускам на изгиб:
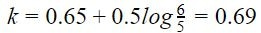
Для получения окончательной длины мы просто прибавляем две длины ног к припуску на подгибку:
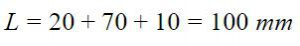
Советы по гибке листового металла:
Итак, я поговорил с нашим опытным менеджером по продажам, который знает толк в гибке листового металла. Он загорелся и решил воспользоваться возможностью и поделиться своими знаниями о гибке листового металла. Таким образом, он привел список распространенных ошибок и решений, как их избежать.
Минимальная длина фланца:
Существует минимальная длина фланца, как уже говорилось ранее. Для ориентировки смотрите таблицу изгибающих усилий. В зависимости от толщины выбирается ширина штампа. Если вы разработаете слишком короткий фланец, он будет неловко "проваливаться" в щель, и вы не получите желаемого результата.
Боковые стороны с фаской:
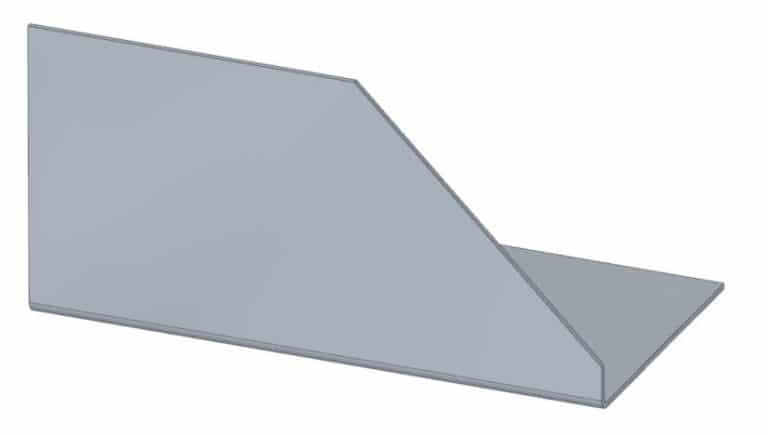
Фаска должна заканчиваться перед основанием детали
Если вы хотите сделать фланец с фаской на одном или двух концах, предыдущее правило о минимальной длине фланца остается в силе. Фаски должны оставлять достаточно места для выполнения правильных изгибов, иначе фланец будет выглядеть деформированным, и никто не будет удовлетворен.
Расстояние от отверстия до изгиба:

Близко расположенные отверстия могут деформироваться
Если отверстия расположены слишком близко к изгибу, они могут деформироваться. Круглые отверстия не так проблематичны, как другие типы, но болты все равно могут не пройти. Опять же, смотрите диаграмму изгибающего усилия для минимальных размеров фланца и размещайте отверстия дальше, чем минимальные.
Симметрия:
Чтобы избежать путаницы, прямоугольное отверстие может быть с обеих сторон
Существует большая опасность при изготовлении деталей, которые почти симметричны. Если возможно, делайте их симметричными. Если деталь почти симметрична, оператор гибочного пресса может запутаться. Результат? Ваша деталь будет согнута в неправильном направлении.
Заклепочные гайки:

Заклепочная гайка на пути гибочного инструмента
Если вы используете заклепочные гайки вблизи линии изгиба, известно, что их установка перед изгибом хороша для обеспечения его применимости. После изгиба отверстия могут деформироваться. Тем не менее, убедитесь, что гайки не будут мешать инструментам при гибке.
Маленькие фланцы для больших деталей:
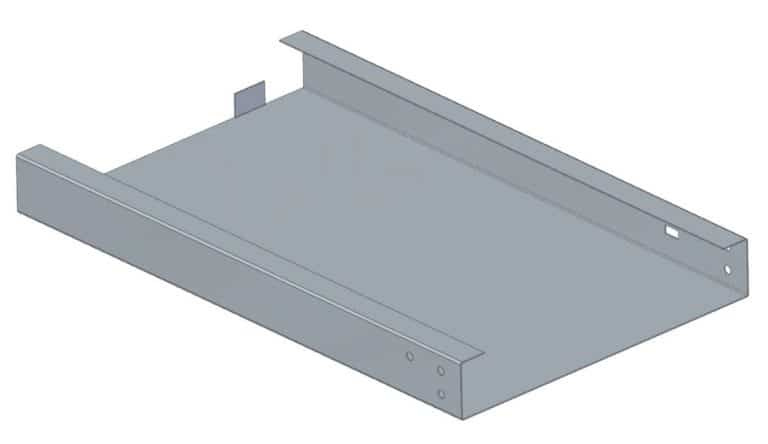
Небольшой изгиб в конце большой детали может привести к трудностям
Лучше отказаться от маленьких фланцев на больших и тяжелых деталях. Это очень усложняет производство, и может потребоваться ручная обработка, которая обойдется дороже, чем простая механическая. В результате, если есть возможность, лучше выбрать альтернативное решение.
Сгибы рядом друг с другом:
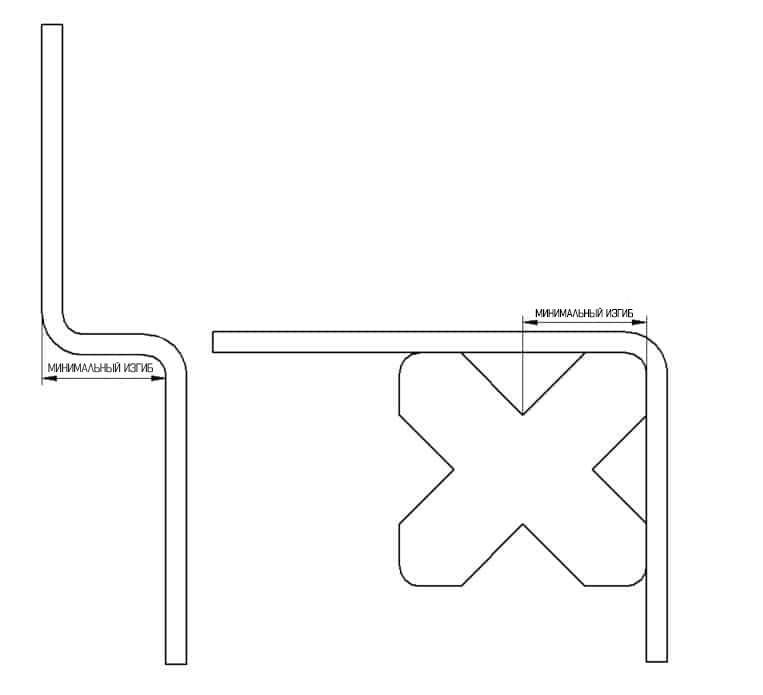
Проверьте таблицу изгибающих усилий для минимальной длины фланца
Если вы хотите включить последовательные изгибы, проверьте, выполнимо ли это. Проблема возникает, когда вы не можете установить уже согнутую деталь на штамп. Если изгибы направлены в одну сторону - U-образный изгиб, - то общее правило заключается в том, что промежуточная часть должна быть длиннее фланцев.
Разместите изгибы на одной линии:

Эта часть нуждается в многочисленных корректировках.
Лучше всего проектировать изгибы на одной линии, если у вас есть несколько фланцев подряд. Имея это в виду, вы можете свести количество операций к минимуму. В противном случае оператору необходимо вносить корректировки для каждого отдельного изгиба, а это означает потерю времени и денег.
Линия изгиба параллельна стороне:
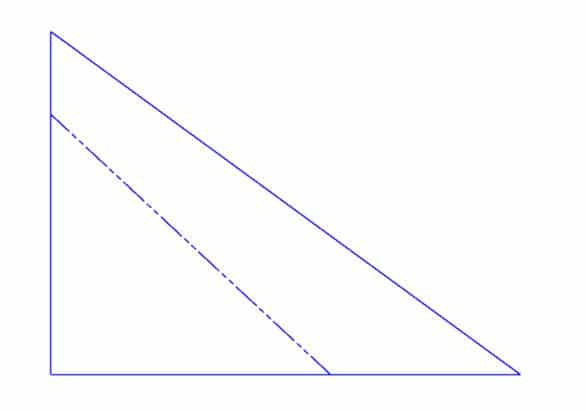
Такой вид линий сгиба приводит к неточным результатам
Как говорится в заголовке. Для целей позиционирования должна быть параллельная сторона вашей линии изгиба. Если её нет, выравнивание детали станет настоящей головной болью, и в итоге вы можете получить неудовлетворительный результат.
Рельеф изгиба:

Рельеф изгиба необходим
Для достижения наилучшего результата рекомендуется сделать не просто небольшой разрез лазером, а настоящий вырез по бокам будущего фланца - который должен быть рельефом изгиба. Ширина такого надреза должна превышать толщину материала. Это гарантирует отсутствие разрывов и деформаций при окончательном изгибе. Другой хорошей практикой здесь является включение небольших радиусов в рельефы изгиба, поскольку они также снимают напряжение материала.
Сгибание коробки:

Небольшие зазоры гарантируют выполнение работы
При сгибании коробки необходимо оставлять небольшие зазоры между фланцами. В противном случае последний сгиб может врезаться в существующие, ломая всю конструкцию.
Проверьте плоский шаблон:
Следует помнить о том, что время от времени нужно переключать вид CAD на плоский шаблон. В этом есть много плюсов. Во-первых, если вы увлечетесь фланцами, в итоге может получиться что-то, что не может существовать в плоской схеме. А то, что не может существовать в плоской схеме, не может существовать и в любой другой.
Измерьте макет. Возможно, вы сможете скорректировать конструкцию для оптимальной посадки. Старайтесь не брать лист большего размера, если меньший размер находится в пределах досягаемости. Может быть, вы сможете уместить 2 детали на одном листе, если просто убавите несколько миллиметров? Это отразится на окончательной цене проекта.
Эмпирическое правило для минимального радиуса изгиба:
Будьте проще. Что может быть проще, чем выбрать внутренний радиус (ir), равный толщине материала. Это позволяет избежать последующих проблем, излишних раздумий и глупых ошибок. Уменьшение радиуса ниже этого значения может привести к проблемам. Больший радиус только усложнит некоторые другие расчеты.
Направление изгиба:
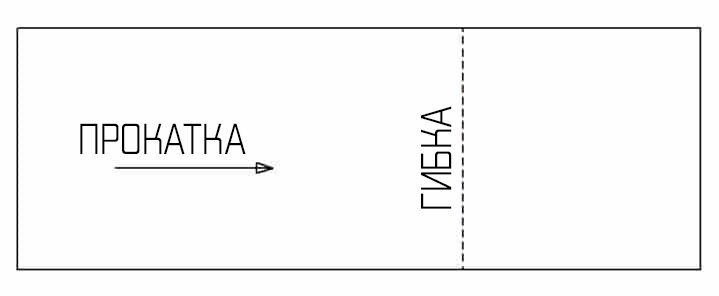
Изгиб перпендикулярно прокатке
Не следует проектировать изгибы в том же направлении, в котором производилась прокатка материала. Это особенно важно для алюминия. Конечно, все мы знаем алюминиевые корпуса с 4 сторонами, которые подразумевают гибочные операции, противоположные тем, что мы предлагаем. Тем не менее, лучше избегать этого, если возможно. Результатом могут стать неровные поверхности или даже трещины.
Хотя инженеры-производители заботятся о том, чтобы замечать такие вещи, полезно замечать их самостоятельно. Это помогает учесть расход материала.
Загиб кромок:
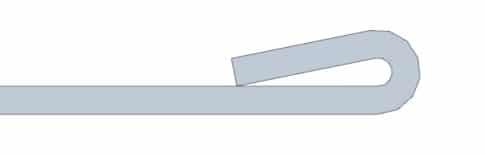
Оставляйте внутренний радиус, если это возможно
Если вы хотите укрепить края металлического листа, то загиб кромок - отличный вариант. Тем не менее, здесь применимы некоторые советы. Лучше оставить небольшой радиус внутри загиба. Для полного разрушения радиуса требуется большая мощность и тоннаж. Кроме того, это подвергает материал опасности растрескивания. Оставление радиуса, напротив, снимает эту опасность.
Оцените материал:
Обычные тонкие листы конструкционной стали толщиной 1. 3 мм могут выдержать практически все. После этого необходимо провести исследование. Некоторые материалы гораздо более капризны в обращении с ними. Получение хорошего результата зависит от ваших знаний и от помощи, которую может оказать ваш инженер-технолог.
Если вам понравилась статья, то ставьте лайк, делитесь ею со своими друзьями и оставляйте комментарии!
Коммерческое предложение
Подтверждаю свое согласие на использование моих персональных данных в соответствии с "Политикой защиты и обработки персональных данных Dreambird".

Официальный дистрибьютор в странах Балтии и СНГ
CAD/CAM и производственные процессы: публикации
Расчеты параметров гибки изделий из листового металла для гибочного пресса

Понимание соотношения между V-образной выемкой, радиусом, допуском на гибку и К-фактором для лучшего выполнения расчетов плоской развертки детали из листового металла.
Иногда на производстве бывают случаи, когда детали из листового металла, вырезанные лазером, полученные путем пробивки или обрезки кажутся "слишком длинными" или "слишком короткими" после их гибки на листогибочном прессе. Бывает также, что изделия, спроектированные на компьютере, не соответствуют реальным размерам после гибки. Производитель инструмента для гибки Rolleri предлагает больше узнать о факторах, которые следует учитывать для достижения наилучших результатов в подобных ситуациях.

Процесс гибки: простые факты
1) Радиус, получающийся за счет гибки металлического листа, влияет на длину, на которую следует обрезать изделие перед гибкой.
2) Полученный радиус гибки на 99% зависит от V-образной выемки, которую мы выбираем для работы.

Простое заключение
До начала проектирования изделия и резки заготовок, следует обязательно знать, какая V-образная выемка будет использоваться для гибки детали на листогибочном станке.

Как радиус влияет на заготовки
Больший радиус раздвинет изделие в сторону внешнего края, оставляя впечатление того, что была отрезана слишком длинная заготовка.
Меньший радиус потребует заготовки, обрезанной "немного длиннее", чем в случае большего радиуса.

Допуск на гибку
Развернутая плоская заготовка профиля, указанного выше на изображении рассчитывается следующим образом:
B = 150 + 100 + 60 + BA1 + BA2
Далее последует обьяснение, как рассчитать параметры ВА1 и ВА2.
Расчет допуска на гибку
Участок, на который нужно укоротить обе стороны, которые совпадут после расплющивания детали, является тем, что обычно называется "допуском на гибку" и обозначаем ВА в формуле.

Формула допуска на гибку (ВА)
Формула BA для сгибов менее 90°

Формула АВ для сгибов от 91°до 165°

iR= внутренний радиус
На нашем сайте вы найдете еще много информации о гибке листового металла! Читайте статью "Оцифровка работы гибочного станка"!
K-фактор (коэффициент положения нейтральной линии)
При гибке на листогибочном станке, внутренняя сторона металлического листа сжимается, а внешняя, наоборот, растягивается. Это означает, что есть место на листе, в котором волокна не сжимаются и не растягиваются. Это место называется "нейтральной линией". Расстояние от внутренней части сгиба до нейтральной линии называется К-фактором, коэффициентом положения нейтральной линии.
Изменить этот коэффициент невозможно, так как он является постоянным для каждого типа материала. Он выражается в виде дробей, и чем меньше К-фактор, тем ближе нейтральная линия будет расположена к внутреннему радиусу листа.

K-фактор = тонкая настройка
Значение К-фактора влияет на плоскую заготовку, возможно, не настолько, как влияет радиус детали, но следует учитывать его при тонкой настройке расчетов для заготовок. Чем меньше К-фактор, тем больше материал растягивается и "выталкивается", заставляя заготовку быть "больше".

Прогнозирование К-фактора
В большинстве случаев мы можем прогнозировать и настраивать К-фактор при выполнении расчетов плоской заготовки.

Необходимо провести несколько испытаний выбранной V-образной выемки и измерить радиус детали. Если необходимо более точно рассчитать К-фактор, можно воспользоваться формулой расчета К-фактора для гибки, приведенной ниже:

Формула К-фактора

Решение примера:
B = 150 + 100 + 60 +BA1 + BA2
Оба сгиба меньше или равны 90°:
B1 = 3.14 x 0.66 x (6 + ((4×0.8)/2) – 2 x 10
B2 = 3.14 x 0.5 x (8 + ((4×0.8)/2) – 2 x 12
B = 150 + 100 + 60 + (-4.25) + (-8.93)
B= 296.8мм
Автор методики: Хулио Алькасер, менеджер международных продаж Rolleri Press Brake Tools
Комментарий Dreambird
Обработка листового металла на современных производствах часто используется для изготовления деталей, точное соблюдение размеров которых критично. Более того, в условиях, когда скорость изготовления ценится превыше всего и от нее зависит, получит ли субподрядчик заказ на изготовление деталей, производители стараются избегать траты времени на выполнение калькуляции вручную, выполнение различных тестов и исправление допущенных ошибок. Использованный в статье метод, несомненно, может считаться точным и изложенные в нем формулы полезны, но постоянное использование их при расчетах ведет к дополнительным временным затратам на производстве.
Сегодняшние листогибочные прессы зачастую оснащены стойками ЧПУ и последовательность гибки конкретного изделия может быть задана на компьютере непосредственно после проектирования изделия. При наличии готового файла с геометрией плоской развертки последовательность гибки, требующаяся для ее выполнения, также рассчитывается на компьютере после непосредственного импорта этого файла в специализированное CAD/CAM-решение для гибки.
Современное автономное программное решение Radbend, часть CAD/CAM-комплекса Radan для обработки листового металла, является мировым лидером среди приложений аналогичного характера. Все изложенные в статье расчеты заложены в Radbend в виде алгоритмов и не требуют расчетов вручную. Гибка детали выполняется в среде Radbend так, как она будет выполнена на самом деле, затем "слишком длинные" стороны подгоняются для абсолютной точности. Далее уже согнутое изделие отправляется в модуль Radan3D, где на его основе создается заготовка, при расчете длины которой учитывается ранее выполненная в Radbend подгонка. Таким образом при производстве изделия будут соблюдены все требуемые параметры и обработка будет выполнена корректно уже с первого подхода.
Radbend позволяет заранее определить технологичность изготовления детали, генерируя и показывая графически полную симуляцию обработки и последовательность гибки, помогая подобрать инструмент и расположить упоры. С помощью этого модуля можно избежать проблем, часто возникающих на производстве - предотвратить столкновения инструмента, изделия и частей станка.
SOLIDWORKS: Листовой металл. Допуск на изгиб, уменьшение изгиба и коэффициент «К»

Расчет изгибов листового металла
Сегодня поговорим о процессе гибки ЛИСТОВОГО МЕТАЛЛА в SOLIDWORKS.
В процессе гибки листового металла, материал по внутреннему радиусу изгиба подвергается сжатию, а по внешнему радиусу изгиба будет растягиваться. Линия перехода от сжатия к растяжению называется нейтральной осью. На нейтральной оси материал не растягивается и не сжимается. Следовательно, длина нейтральной оси остается неизменной до и после операции гибки. Расположение нейтральной оси зависит от физических свойств материала и его толщины. Важно знать расположение нейтральной оси для конкретного листа, поскольку все расчеты разверток производятся на основе нейтральной оси. Расположение нейтральной оси для конкретного листа определяется коэффициентом, называемым «К».
Коэффициент «К»
Коэффициент «К» это соотношение, которое представляет положение нейтральной оси по отношению к толщине детали из листового металла и зависит от материала, толщины и радиуса изгиба. Коэффициент «К» можно определить следующим образом:
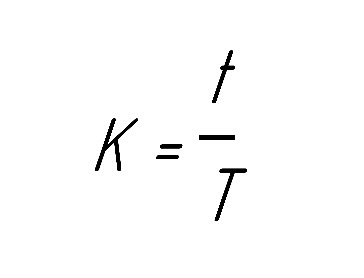
Формула расчета коэффициента "К"
Где t - расстояние от внутренней поверхности до нейтральной оси, а T - толщина листа (рисунок 1). На практике коэффициент «К» применяется, когда не известно, какой процесс или машина будут использованы для сгибания листа.
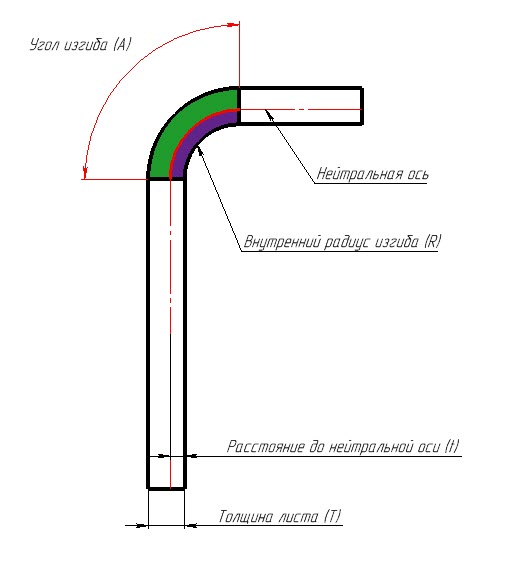
Рисунок 1: Нейтральная ось согнутого листа
Допуск на изгиб (ВА)
Допуск на изгиб (ВА) — длина дуги изгиба, измеренная вдоль нейтральной оси материала. Понимание допуска на изгиб и, следовательно, уменьшения изгиба детали - важный первый шаг к пониманию того, как изготавливаются детали из листового металла.
Когда листовой металл подвергается процессу изгиба, металл вокруг изгиба деформируется и растягивается. По мере того, как это происходит, получается небольшая общая длина части листа. Допуск на изгиб определяется как материал, который нужно будет добавить к начальной длине плоского листа, чтобы получить длину формованной детали. Как уже упоминалось ранее, длина нейтральной оси после изгиба не меняется. Таким образом, следующее уравнение действительно всегда:
Начальная длина = длина первого участка + допуск на изгиб + длина второго участка.

Рисунок 2: Допуск на изгиб
Вычисление изгиба
Важно учесть, что при разработке развертки, необходимо сделать вычет из желаемого размера детали, чтобы получить правильный размер развертки. Уменьшение изгиба определяется как материал, который придется удалить из общей длины сгибов, чтобы получить развертку. Чтобы произвести расчет нужно переписать предыдущее уравнение как:
Начальная длина = (длина сгиба 1 – внешний отступ) + допуск на изгиб + (длина сгиба 2 - внешний отступ)
Начальная длина = длина фланца 1 + длина фланца 2 - (2 * внешний отступ - допуск на изгиб)
Вычет изгиба (BD) – представляет собой разницу между допуском изгиба и удвоенным внешним отступом.
Вычет изгиба (BD) = 2* внешний отступ- допуск на изгиб.
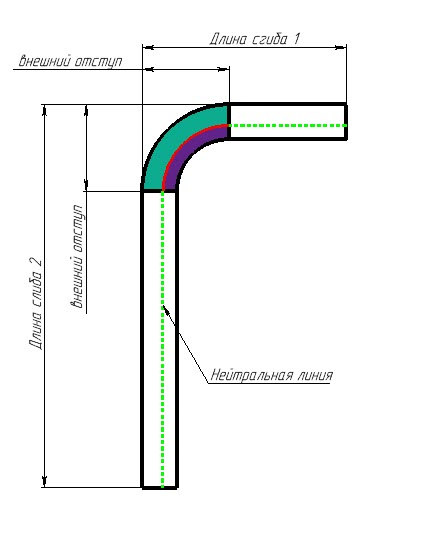
Изгиб
Допуск на изгиб и уменьшение изгиба можно рассчитать с использованием коэффициента К следующим образом:
Читайте также:
