При фотоэффекте работа выхода электронов из металла
Работа выхода — разница между минимальной энергией (обычно измеряемой в электрон-вольтах), которую необходимо сообщить электрону для его «непосредственного» удаления из объёма твёрдого тела, и энергией Ферми. Здесь «непосредственность» означает то, что электрон удаляется из твёрдого тела через данную поверхность и перемещается в точку, которая расположена достаточно далеко от поверхности по атомным масштабам (чтобы электрон прошёл весь двойной слой), но достаточно близко по сравнению с размерами макроскопических граней кристалла. При этом пренебрегают дополнительной работой, которую необходимо затратить на преодоление внешних полей, возникающих из-за перераспределения поверхностных зарядов. Таким образом, работа выхода для одного и того же вещества для различных кристаллографических ориентаций поверхности оказывается различной.
При удалении электрона на бесконечность его взаимодействие с зарядами, остающимися внутри твёрдого тела приводит к индуцированию макроскопических поверхностных зарядов (при рассмотрении полубесконечного образца в электростатике это называют «изображением заряда»). При перемещении электрона в поле индуцированного заряда совершается дополнительная работа, которая определяется диэлектрической проницаемостью вещества, геометрией образца и свойствами других поверхностей. За счет этого полная работа по перемещению электрона из любой точки образца в любую другую точку (в том числе и точку бесконечности) не зависит от пути перемещения, то есть от того, через какую поверхность был удален электрон. Поэтому в физике твёрдого тела эта работа не учитывается и не входит в работу выхода.
Содержание
Работа выхода в фотоэффекте
Работа выхода в внешнем фотоэффекте - минимальная энергия, необходимая для удаления электрона из вещества под действием света
Измерение работы выхода
Единицами измерения работы выхода являются Джоуль (Дж) или электронвольт (эВ).
Работа выхода электрона из различных металлов
Единица измерения: эВ электронвольт
Источник: CRC Handbook of Chemistry and Physics version 2008, стр. 12-114.
Примечание: Работа выхода может зависеть от ориентации освещаемого кристалла. К примеру, Ag: 4.26, Ag(100): 4.64, Ag(110): 4.52, Ag(111): 4.74. Диапазоны изменения работы выхода для типичных кристаллографических направлений указаны в таблице.
Литература
- Физика поверхности
- Физика твёрдого тела
- Физика полупроводников
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое "Работа выхода" в других словарях:
РАБОТА ВЫХОДА — энергия Ф, к рую необходимо затратить для удаления эл на из твёрдого или жидкого в ва в вакуум (в состояние с равной нулю кинетич, энергией). Р. в. Ф=еj, где j потенциал Р. в., е абс. величина электрич. заряда электрона. Р. в. равна разности… … Физическая энциклопедия
работа выхода — электрона; работа выхода Работа, соответствующая разности энергий между уровнем химического потенциала в теле и уровнем потенциала вблизи поверхности тела вне его при отсутствии электрического поля … Политехнический терминологический толковый словарь
РАБОТА ВЫХОДА — работа, которую необходимо затратить для удаления электрона из конденсированного вещества в вакуум. Измеряется разностью между минимальной энергией электрона в вакууме и Ферми энергией электронов внутри тела. Зависит от состояния поверхности… … Большой Энциклопедический словарь
РАБОТА ВЫХОДА — РАБОТА ВЫХОДА, энергия, затрачиваемая на удаление электрона из вещества. Учитывается при ФОТОЭЛЕКТРИЧЕСКОМ ЭФФЕКТЕ и в ТЕРМОЭЛЕКТРОНИКЕ … Научно-технический энциклопедический словарь
работа выхода — Энергия, необходимая для переноса в бесконечность электрона, находящегося в исходном положении на уровне Ферми в данном материале. [ГОСТ 13820 77] Тематики электровакуумные приборы … Справочник технического переводчика
работа выхода — [work function] энергия, затрачиваемая на удаление электрона из твердого тела или жидкости в вакуум. Переход электрона из вакуума в конденсированную среду сопровождается выделением энергии, равной работе выхода; чем меньше работа выхода, тем… … Энциклопедический словарь по металлургии
работа выхода — Work Function Работа выхода Минимальная энергия (обычно измеряемая в электрон вольтах), которую необходимо затратить для удаления электрона из объема твёрдого тела. Электрон удаляется из твердого тела через данную поверхность и перемещается в … Толковый англо-русский словарь по нанотехнологии. - М.
работа выхода — работа, которую необходимо затратить для удаления электрона из конденсированного вещества в вакуум. Измеряется разностью между минимальной энергией электрона в вакууме и ферми энергией электронов внутри тела. Зависит от состояния поверхности… … Энциклопедический словарь
работа выхода — išlaisvinimo darbas statusas T sritis Standartizacija ir metrologija apibrėžtis Darbas, kurį atlieka 1 molis dalelių (atomų, molekulių, elektronų) pereidamas iš vienos fazės į kitą arba į vakuumą. atitikmenys: angl. work function vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
работа выхода — išlaisvinimo darbas statusas T sritis fizika atitikmenys: angl. work function; work of emission; work of exit vok. Ablösearbeit, f; Auslösearbeit, f; Austrittsarbeit, f rus. работа выхода, f pranc. travail de sortie, m … Fizikos terminų žodynas
48. Квантовая и ядерная физика Читать 0 мин.
Свет обладает двойственной природой: в некоторых случаях он ведет себя как волна, в других ― как частица. При фотоэффекте свет ведет себя как частица. «Порции» света (кванты) ― фотоны. Энергия одного фотона прямо пропорциональна его частоте и равна Ev = hv, где
h ― постоянная Планка, равная 6,6 ∙ 10-34 [Дж∙с];
Фотоэффект (фотоэлектрический эффект) ― испускание электронов веществом под действием света.
Свет поглощают электроны, свободно расположенные в металле. Поглотив квант света, электрон увеличивает свою энергию настолько, что может вылететь из металла. Таким образом, фотоны «выбивают» электроны из металла, если их энергия достаточно велика для этого. Электроны, вылетевшие под действием света (фотонов) называются фотоэлектронами. Поскольку ток ― это направленный поток заряженных частиц ― то при облучении металла светом достаточной энергии, создается ток, который называется фототоком.
Металлическая пластинка, подключенная к электрической цепи, и облучаемая светом, называется фотокатодом.
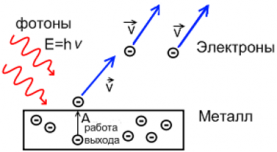
Энергия и скорость вылетающих электронов зависит от частоты падающего света ― т. е энергии фотона, который выбивает электрон. Скорость фотоэлектронов тем выше, чем выше частота фотонов. Аналогично, скорость фотоэлектронов тем меньше, чем меньше частота падающих фотонов.
Энергия и скорость вылетающих электронов от интенсивности света не зависят.
Дело в том, что интенсивность (яркость) света определяет не то, какую энергию имеют фотоны (напомним, что энергия фотонов зависит от их частоты), а то, сколько будет этих фотов в свете. Если свет яркий ― в нём находится много фотонов, если свет не яркий ― не много.
Теоретически фотоэффект объяснил Эйнштейн. Формула Эйнштейна для фотоэффекта связывает энергию падающих фотонов и энергию вылетающих электронов: hv = A + EК, где
EК ― кинетическая энергия фотона. [Дж].
Работа выхода фотоэффекта ― постоянная величина и зависит только от природы металла и состояния его поверхности. Работа выхода не зависит от частоты или интенсивности света.
Как видно из формулы Эйнштейна, энергия фотона идет на совершение работы выхода и на увеличение кинетической энергии электрона. Так как работа выхода постоянна, то при уменьшении частоты света ― уменьшается кинетическая энергия, а значит, и скорость вылетающих электронов. Если частота света уменьшается до предельной величины ― частоты красной границы фотоэффекта, скорость электронов становится равной нулю и фотоэффект прекращается. Если частота света меньше частоты красной границы фотоэффекта ― то фотоэффект не наблюдается, поскольку энергии фотонов недостаточно для того, чтобы выбить электрон из материала.
Красная граница фотоэффекта ― это частота, при которой прекращается фотоэффект. Ее можно определить из условия $hv_> = A$ , где
vкрасная граница ― частота света [Гц];
График зависимости кинетической энергии вылетающих электронов от частоты падающих фотонов:
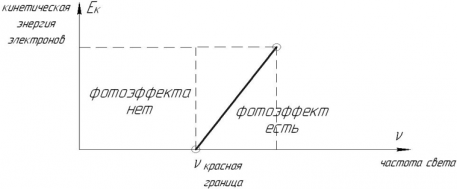
Запирающее напряжение ― это напряжение, не позволяющее электронам покинуть фотокатод. Если напряжение в цепи больше или равно запирающему напряжению, то электроны не могут достигнуть анода: даже если они покидают ненадолго фотокатод, сила электрического поля возвращает их в металл ― и фототока в цепи нет.
Запирающее напряжение определяется выражением eUзап = Eкинетическая, где
e ― заряд электрона равный 1,6 ∙ 10-19 [Кл];
Uзап ― запирающее напряжение [В];
Eкинетическая ― кинетическая энергия фотоэлектрона [Дж].
Когда напряжение в цепи равно нулю U = 0, а фотокатод облучается светом достаточной энергии, чтоб создавать фотоэффект, ― в сети есть ток, его вызывают выбиваемые светом электроны.
Когда напряжение в цепи равно запирающему напряжению U = Uз ― сила тока становится равной нулю, т. к. фототок прекращается.
Как видно из формулы, запирающее напряжение зависит только от кинетической энергии электронов, которая, в свою очередь, зависит от частоты света (но не интенсивности) и работы выхода.
Фотоэффект
Фотоэффект — это выбивание электронов из вещества падающим светом. Явление фотоэффекта было открыто Генрихом Герцем в 1887 году в ходе его знаменитых экспериментов по излучению электромагнитных волн.
Напомним, что Герц использовал специальный разрядник (вибратор Герца) — разрезанный пополам стержень с парой металлических шариков на концах разреза. На стержень подавалось высокое напряжение, и в промежутке между шариками проскакивала искра. Так вот, Герц обнаружил, что при облучении отрицательно заряженного шарика ультрафиолетовым светом проскакивание искры облегчалось.
Герц, однако, был поглощён исследованием электромагнитных волн и не принял данный факт во внимание. Год спустя фотоэффект был независимо открыт русским физиком Александром Григорьевичем Столетовым. Тщательные экспериментальные исследования, проведённые Столетовым в течение двух лет, позволили сформулировать основные законы фотоэффекта.
Опыты Столетова
В своих знаменитых экспериментах Столетов использовал фотоэлемент собственной конструкции (Фотоэлементом называется любое устройство, позволяющее наблюдать фотоэффект). Его схема изображена на рис. 1 .

Рис. 1. Фотоэлемент Столетова
В стеклянную колбу, из которой выкачан воздух (чтобы не мешать лететь электронам), введены два электрода: цинковый катод и анод . На катод и анод подаётся напряжение, величину которого можно менять с помощью потенциометра и измерять вольтметром .
Сейчас на катод подан «минус», а на анод — «плюс», но можно сделать и наоборот (и эта перемена знака — существенная часть опытов Столетова). Напряжению на электродах приписывается тот знак, который подан на анод (Поэтому поданное на электроды напряжение часто называют анодным напряжением). В данном случае, например, напряжение положительно.
Катод освещается ультрафиолетовыми лучами УФ через специальное кварцевое окошко, сделанное в колбе (стекло поглощает ультрафиолет, а кварц пропускает). Ультрафиолетовое излучение выбивает с катода электроны , которые разгоняются напряжением и летят на анод. Включённый в цепь миллиамперметр регистрирует электрический ток. Этот ток называется фототоком, а выбитые электроны, его создающие, называются фотоэлектронами.
В опытах Столетова можно независимо варьировать три величины: анодное напряжение, интенсивность света и его частоту.
Зависимость фототока от напряжения
Меняя величину и знак анодного напряжения, можно проследить, как меняется фототок. График этой зависимости, называемый характеристикой фотоэлемента, представлен на рис. 2 .

Рис. 2. Характеристика фотоэлемента
Давайте обсудим ход полученной кривой. Прежде всего заметим, что электроны вылетают из катода с различными скоростями и в разных направлениях; максимальную скорость, которую имеют фотоэлектроны в условиях опыта, обозначим .
Если напряжение отрицательно и велико по модулю, то фототок отсутствует. Это легко понять: электрическое поле, действующее на электроны со стороны катода и анода, является тормозящим (на катоде «плюс», на аноде «минус») и обладает столь большой величиной, что электроны не в состоянии долететь до анода. Начального запаса кинетической энергии не хватает — электроны теряют свою скорость на подступах к аноду и разворачиваются обратно на катод. Максимальная кинетическая энергия вылетевших электронов оказывается меньше, чем модуль работы поля при перемещении электрона с катода на анод:
Здесь кг — масса электрона, Кл — его заряд.
Будем постепенно увеличивать напряжение, т.е. двигаться слева направо вдоль оси из далёких отрицательных значений.
Поначалу тока по-прежнему нет, но точка разворота электронов становится всё ближе к аноду. Наконец, при достижении напряжения , которое называется задерживающим напряжением, электроны разворачиваются назад в момент достижения анода (иначе говоря, электроны прибывают на анод с нулевой скоростью). Имеем:
Таким образом, величина задерживающего напряжения позволяет определить максимальную кинетическую энергию фотоэлектронов.
При небольшом превышении задерживающего напряжения появляется слабый фототок. Его формируют электроны, вылетевшие с максимальной кинетической энергией почти точно вдоль оси колбы (т.е. почти перпендикулярно катоду): теперь электронам хватает этой энергии, чтобы добраться до анода с ненулевой скоростью и замкнуть цепь. Остальные электроны, которые имеют меньшие скорости или полетели в сторону от анода, на анод не попадают.
При повышении напряжения фототок увеличивается. Анода достигает большее количество электронов, вылетающих из катода под всё большими углами к оси колбы. Обратите внимание, что фототок присутствует при нулевом напряжении!
Когда напряжение выходит в область положительных значений, фототок продолжает возрастать. Оно и понятно: электрическое поле теперь разгоняет электроны, поэтому всё большее их число получают шанс оказаться на аноде. Однако достигают анода пока ещё не все фотоэлектроны. Например, электрон, вылетевший с максимальной скоростью перпендикулярно оси колбы (т.е. вдоль катода), хоть и развернётся полем в нужном направлении, но не настолько сильно, чтобы попасть на анод.
Наконец, при достаточно больших положительных значениях напряжения ток достигает своей предельной величины , называемой током насыщения, и дальше возрастать перестаёт.
Почему? Дело в том, что напряжение, ускоряющее электроны, становится настолько велико, что анод захватывает вообще все электроны, выбитые из катода — в каком бы направлении и с какими бы скоростями они не начинали движение. Стало быть, дальнейших возможностей увеличиваться у фототока попросту нет — ресурс, так сказать, исчерпан.
Законы фотоэффекта
Величина тока насыщения — это, по существу, количество электронов, выбиваемых из катода за одну секунду. Будем менять интенсивность света, не трогая частоту. Опыт показывает, что ток насыщения меняется пропорционально интенсивности света.
Первый закон фотоэффекта. Число электронов, выбиваемых из катода за секунду, пропорционально интенсивности падающего на катод излучения (при его неизменной частоте).
Ничего неожиданного в этом нет: чем больше энергии несёт излучение, тем ощутимее наблюдаемый результат. Загадки начинаются дальше.
А именно, будем изучать зависимость максимальной кинетической энергии фотоэлектронов от частоты и интенсивности падающего света. Сделать это несложно: ведь в силу формулы (1) нахождение максимальной кинетической энергии выбитых электронов фактически сводится к измерению задерживающего напряжения.
Сначала меняем частоту излучения при фиксированной интенсивности. Получается такой график (рис. 3 ):

Рис. 3. Зависимость энергии фотоэлектронов от частоты света
Как видим, существует некоторая частота , называемая красной границей фотоэффекта, разделяющая две принципиально разные области графика. Если , то фотоэффекта нет.
Если же \nu_0' alt='\nu > \nu_0' /> , то максимальная кинетическая энергия фотоэлектронов линейно растёт с частотой.
Теперь, наоборот, фиксируем частоту и меняем интенсивность света. Если при этом , то фотоэффект не возникает, какова бы ни была интенсивность! Не менее удивительный факт обнаруживается и при \nu_0' alt='\nu > \nu_0' /> : максимальная кинетическая энергия фотоэлектронов от интенсивности света не зависит.
Все эти факты нашли отражение во втором и третьем законах фотоэффекта.
Второй закон фотоэффекта. Максимальная кинетическая энергия фотоэлектронов линейно возрастает с частотой света и не зависит от его интенсивности.
Третий закон фотоэффекта. Для каждого вещества существует красная граница фотоэффекта — наименьшая частота света , при которой фотоэффект ещё возможен. При фотоэффект не наблюдается ни при какой интенсивности света.
Трудности классического объяснения фотоэффекта
Как можно было бы объяснить фотоэффект с точки зрения классической электродинамики и волновых представлений о свете?
Известно, что для вырывания электрона из вещества требуется сообщить ему некоторую энергию , называемую работой выхода электрона. В случае свободного электрона в металле это работа по преодолению поля положительных ионов кристаллической решётки, удерживающего электрон на границе металла. В случае электрона, находящегося в атоме, работа выхода есть работа по разрыву связи электрона с ядром.
В переменном электрическом поле световой волны электрон начинает совершать колебания.
И если энергия колебаний превысит работу выхода, то электрон будет вырван из вещества.
Однако в рамках таких представлений невозможно понять второй и третий законы фотоэффекта. Действительно, почему кинетическая энергия выбитых электронов не зависит от интенсивности излучения? Ведь чем больше интенсивность, тем больше напряжённость электрического поля в электромагнитной волне, тем больше сила, действующая на электрон, тем больше энергия его колебаний и с тем большей кинетической энергией электрон вылетит из катода. Логично? Логично. Но эксперимент показывает иное.
Далее, откуда берётся красная граница фотоэффекта? Чем «провинились» низкие частоты? Казалось бы, с ростом интенсивности света растёт и сила, действующая на электроны; поэтому даже при низкой частоте света электрон рано или поздно будет вырван из вещества — когда интенсивность достигнет достаточно большого значения. Однако красная граница ставит жёсткий запрет на вылет электронов при низких частотах падающего излучения.
Кроме того, неясна безынерционность фотоэффекта. Именно, при освещении катода излучением сколь угодно слабой интенсивности (с частотой выше красной границы) фотоэффект начинается мгновенно — в момент включения освещения. Между тем, казалось бы, электронам требуется некоторое время для «расшатывания» связей, удерживающих их в веществе, и это время «раскачки» должно быть тем больше, чем слабее падающий свет. Аналогия такая: чем слабее вы толкаете качели, тем дольше придётся их раскачивать до заданной амплитуды.
Выглядит опять-таки логично, но опыт — единственный критерий истины в физике! — этим доводам противоречит.
Так на рубеже XIX и XX столетий в физике возникла тупиковая ситуация: электродинамика, предсказавшая существование электромагнитных волн и великолепно работающая в диапазоне радиоволн, отказалась объяснять явление фотоэффекта.
Выход из этого тупика был найден Альбертом Эйнштейном в 1905 году. Он нашёл простое уравнение, описывающее фотоэффект. Все три закона фотоэффекта оказались следствиями уравнения Эйнштейна.
Главная заслуга Эйнштейна состояла в отказе от попыток истолковать фотоэффект с позиций классической электродинамики. Эйнштейн привлёк к делу смелую гипотезу о квантах, высказанную Максом Планком пятью годами ранее.
Гипотеза Планка о квантах
Классическая электродинамика отказалась работать не только в области фотоэффекта. Она также дала серьёзный сбой, когда её попытались использовать для описания излучения нагретого тела (так называемого теплового излучения).
Суть проблемы состояла в том, что простая и естественная электродинамическая модель теплового излучения приводила к бессмысленному выводу: любое нагретое тело, непрерывно излучая, должно постепенно потерять всю свою энергию и остыть до абсолютного нуля. Как мы прекрасно знаем, ничего подобного не наблюдается.
В ходе решения этой проблемы Макс Планк высказал свою знаменитую гипотезу.
Гипотеза о квантах. Электромагнитная энергия излучается и поглощается не непрерывно, а отдельными неделимыми порциями — квантами. Энергия кванта пропорциональна частоте излучения:
Cоотношение (2) называется формулой Планка, а коэффициент пропорциональности — постоянной Планка.
Принятие этой гипотезы позволило Планку построить теорию теплового излучения, прекрасно согласующуюся с экспериментом. Располагая известными из опыта спектрами теплового излучения, Планк вычислил значение своей постоянной:
Успешность гипотезы Планка наводила на мысль, что законы классической физики неприменимы к малым частицам вроде атомов или электронов, а также к явлениям взаимодействия света и вещества. Подтверждением данной мысли как раз и послужило явление фотоэффекта.
Уравнение Эйнштейна для фотоэффекта
Гипотеза Планка говорила о дискретности излучения и поглощения электромагнитных волн, то есть о прерывистом характере взаимодействия света с веществом. При этом Планк считал, что распространение света — это непрерывный процесс, происходящий в полном соответствии с законами классической электродинамики.
Эйнштейн пошёл ещё дальше: он предположил, что свет в принципе обладает прерывистой структурой: не только излучение и поглощение, но также и распространение света происходит отдельными порциями — квантами, обладающими энергией .
Планк рассматривал свою гипотезу лишь как математический трюк и не решился опровергнуть электродинамику применительно к микромиру. Физической реальностью кванты стали благодаря Эйнштейну.
Кванты электромагнитного излучения (в частности, кванты света) стали впоследствии называться фотонами. Таким образом, свет состоит из особых частиц — фотонов, движущихся в вакууме со скоростью .
Каждый фотон монохроматического света, имеющего частоту , несёт энергию .
Фотоны могут обмениваться энергией и импульсом с частицами вещества (об импульсе фотона речь пойдёт в следующем листке); в таком случае мы говорим о столкновении фотона и частицы. В частности, происходит столкновение фотонов с электронами металла катода.
Поглощение света — это поглощение фотонов, то есть неупругое столкновение фотонов с частицами (атомами, электронами). Поглощаясь при столкновении с электроном, фотон передаёт ему свою энергию. В результате электрон получает кинетическую энергию мгновенно, а не постепенно, и именно этим объясняется безынерционность фотоэффекта.
Уравнение Эйнштейна для фотоэффекта есть не что иное, как закон сохранения энергии. На что идёт энергия фотона ? при его неупругом столкновении с электроном? Она расходуется на совершение работы выхода по извлечению электрона из вещества и на придание электрону кинетической энергии :
Слагаемое оказывается максимальной кинетической энергией фотоэлектронов. Почему максимальной? Этот вопрос требует небольшого пояснения.
Электроны в металле могут быть свободными и связанными. Свободные электроны «гуляют» по всему металлу, связанные электроны «сидят» внутри своих атомов. Кроме того, электрон может находиться как вблизи поверхности металла, так и в его глубине.
Ясно, что максимальная кинетическая энергия фотоэлектрона получится в том случае, когда фотон попадёт на свободный электрон в поверхностном слое металла — тогда для выбивания электрона достаточно одной лишь работы выхода.
Во всех других случаях придётся затрачивать дополнительную энергию — на вырывание связанного электрона из атома или на «протаскивание» глубинного электрона к поверхности.
Эти лишние затраты приведут к тому, что кинетическая энергия вылетевшего электрона окажется меньше.
Замечательное по простоте и физической ясности уравнение (4) содержит в себе всю теорию фотоэффекта. Давайте посмотрим, какое объяснение получают законы фотоэффекта с точки зрения уравнения Эйнштейна.
1. Число выбиваемых электронов пропорционально числу поглощённых фотонов. С увеличением интенсивности света количество фотонов, падающих на катод за секунду, возрастает.
Стало быть, пропорционально возрастает число поглощённых фотонов и, соответственно, число выбитых за секунду электронов.
2. Выразим из формулы (4) кинетическую энергию:
Действительно, кинетическая энергия выбитых электронов линейно растёт с частотой и не зависит от интенсивности света.
Зависимость кинетической энергии от частоты имеет вид уравнения прямой, проходящей через точку . Этим полностью объясняется ход графика на рис. 3 .
3. Для того, чтобы начался фотоэффект, энергии фотона должно хватить как минимум на совершение работы выхода: . Наименьшая частота , определяемая равенством
как раз и будет красной границей фотоэффекта. Как видим, красная граница фотоэффекта определяется только работой выхода, т.е. зависит лишь от вещества облучаемой поверхности катода.
Если , то фотоэффекта не будет — сколько бы фотонов за секунду не падало на катод. Следовательно, интенсивность света роли не играет; главное — хватает ли отдельному фотону энергии, чтобы выбить электрон.
Уравнение Эйнштейна (4) даёт возможность экспериментального нахождения постоянной Планка. Для этого надо предварительно определить частоту излучения и работу выхода материала катода, а также измерить кинетическую энергию фотоэлектронов.
В ходе таких опытов было получено значение , в точности совпадающее с (3) . Такое совпадение результатов двух независимых экспериментов — на основе спектров теплового излучения и уравнения Эйнштейна для фотоэффекта — означало, что обнаружены совершенно новые «правила игры», по которым происходит взаимодействие света и вещества. В этой области классическая физика в лице механики Ньютона и электродинамики Максвелла уступает место квантовой физике — теории микромира, построение которой продолжается и сегодня.
Урок 22. Фотоэффект
Квантовая физика - раздел теоретической физики, в котором изучаются квантово-механические и квантово-полевые системы и законы их движения.
Фотоэффект – это вырывание электронов из вещества под действием света.
Квант - (от лат. quantum — «сколько») — неделимая порция какой-либо величины в физике.
Ток насыщения - некоторое предельное значение силы фототока.
Задерживающее напряжение - минимальное обратное напряжение между анодом и катодом, при котором фототок равен нулю.
Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл. которую нужно сообщить электрону, для того чтобы он мог преодолеть силы, удерживающие его внутри металла.
Красная граница фотоэффекта – это минимальная частота или максимальная длина волны света излучения, при которой еще возможен внешний фотоэффект.
Основная и дополнительная литература по теме урока:
1. Мякишев Г. Я., Буховцев Б. Б., Чаругин В. М. Физика. 11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 259 – 267.
2. Рымкевич А. П. Сборник задач по физике. 10-11 класс.- М.:Дрофа,2009. – С. 153 – 158.
3. Элементарный учебник физики. Учебное пособие в 3 т./под редакцией академика Ландсберга Г. С.: Т.3. Колебания и волны. Оптика. Атомная и ядерная физика. – 12-е изд. – М.: ФИЗМАТЛИТ, 2001. С. 422 – 429.
4. Тульчинский М. Е. Качественные задачи по физике в средней школе. Пособие для учителей. Изд. 4-е, переработ. и доп. М. «Просвещение», 1972. С. 157.
Теоретический материал для самостоятельного изучения
В начале 20-го века в физике произошла величайшая революция. Попытки объяснить наблюдаемые на опытах закономерности распределения энергии в спектрах теплового излучения оказались несостоятельными. Законы электромагнетизма Максвелла неожиданно «забастовали». Противоречия между опытом и практикой были разрешены немецким физиком Максом Планком.
Гипотеза Макса Планка: атомы испускают электромагнитную энергию не непрерывно, а отдельными порциями – квантами. Энергия Е каждой порции прямо пропорциональна частоте ν излучения света: E = hν.
Коэффициент пропорциональности получил название постоянной Планка, и она равна:
h = 6,63 ∙ 10 -34 Дж∙с.
После открытия Планка начала развиваться самая современная и глубокая физическая теория – квантовая физика.
Квантовая физика - раздел теоретической физики, в котором изучаются квантово-механические и квантово-полевые системы и законы их движения.
Поведение всех микрочастиц подчиняется квантовым законам. Но впервые квантовые свойства материи были обнаружены именно при исследовании излучения и поглощения света.
В 1886 году немецкий физик Густав Людвиг Герц обнаружил явление электризации металлов при их освещении.
Явление вырывания электронов из вещества под действием света называется внешним фотоэлектрическим эффектом.
Законы фотоэффекта были установлены в 1888 году профессором московского университета Александром Григорьевичем Столетовым.

Схема установки для изучения законов фотоэффекта
Первый закон фотоэффекта: фототок насыщения - максимальное число фотоэлектронов, вырываемых из вещества за единицу времени, - прямо пропорционален интенсивности падающего излучения.

Зависимость силы тока от приложенного напряжения
Увеличение интенсивности света означает увеличение числа падающих фотонов, которые выбивают с поверхности металла больше электронов.
Второй закон фотоэффекта: максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности падающего излучения и линейно возрастает с увеличением частоты падающего излучения.
Третий закон фотоэффекта: для каждого вещества существует граничная частота такая, что излучение меньшей частоты не вызывает фотоэффекта, какой бы ни была интенсивность падающего излучения. Эта минимальная частота излучения называется красной границей фотоэффекта.
где Ав – работа выхода электронов;
h – постоянная Планка;
νmin - частота излучения, соответствующая красной границе фотоэффекта;
с – скорость света;
λкр – длина волны, соответствующая красной границе.
Фотоэффект практически безынерционен: фототок возникает одновременно с освещением катода с точностью до одной миллиардной доли секунды.
Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.
Для большинства веществ фотоэффект возникает только под действием ультрафиолетового облучения. Однако некоторые металлы, например, литий, натрий и калий, испускают электроны и при облучении видимым светом.
Известно, что фототоком можно управлять, подавая на металлические пластины различные напряжения. Если на систему подать небольшое напряжение обратной полярности, "затрудняющее" вылет электронов, то ток уменьшится, так как фотоэлектронам, кроме работы выхода, придется совершать дополнительную работу против сил электрического поля.
Задерживающее напряжение - минимальное обратное напряжение между анодом и катодом, при котором фототок равен нулю.
Максимальная кинетическая энергия электронов выражается через задерживающее напряжение:
гдеЕ – заряд электрона;
Теорию фотоэффекта разработал Альберт Эйнштейн. На основе квантовых представлений Эйнштейн объяснил фотоэффект. Электрон внутри металла после поглощения одного фотона получает порцию энергии и стремится вылететь за пределы кристаллической решетки, т.е. покинуть поверхность твердого тела. При этом часть полученной энергии он израсходует на совершение работы по преодолению сил, удерживающих его внутри вещества. Остаток энергии будет равен кинетической энергии:
В 1921 году Альберт Эйнштейн стал обладателем Нобелевской премии, которая, согласно официальной формулировке, была вручена «за заслуги перед теоретической физикой и особенно за открытие закона фотоэлектрического эффекта».
Если фотоэффект сопровождается вылетом электронов с поверхности вещества, то его называют внешним фотоэффектом или фотоэлектронной эмиссией, а вылетающие электроны - фотоэлектронами. Если фотоэффект не сопровождается вылетом электронов с поверхности вещества, то его называют внутренним.
Примеры и разбор решения заданий
1. Монохроматический свет с длиной волны λ падает на поверхность металла, вызывая фотоэффект. Фотоэлектроны тормозятся электрическим полем. Как изменятся работа выхода электронов с поверхности металла и запирающее напряжение, если уменьшить длину волны падающего света?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Работа выхода
Запирающее напряжение
Работа выхода - это характеристика металла, следовательно, работа выхода не изменится при изменении длины волны падающего света.
Запирающее напряжение - это такое минимальное напряжение, при котором фотоэлектроны перестают вылетать из металла. Оно определяется из уравнения:
Следовательно, при уменьшении длины волны падающего света, запирающее напряжение увеличивается.
2. Красная граница фотоэффекта для вещества фотокатода λ0 = 290 нм. При облучении катода светом с длиной волны λ фототок прекращается при напряжении между анодом и катодом U = 1,5 В. Определите длину волны λ.
Запишем уравнение для фотоэффекта через длину волны:
Условие связи красной границы фотоэффекта и работы выхода:
Запишем выражение для запирающего напряжения – условие равенства максимальной кинетической энергии электрона и изменения его потенциальной энергии при перемещении в электростатическом поле:
Решая систему уравнений (1), (2), (3), получаем формулу для вычисления длины волны λ:
Работа выхода электронов из металла. Контактные явления
Электроны проводимости в кристалле находятся в потенциальной яме. Выход из нее требует совершения работы по преодолению силы, действующей на электрон со стороны кристалла. Найдем эту силу. Обладая энергией теплового движения, электроны могут выскакивать из кристалла на расстояние в несколько периодов. Вышедший из кристалла и находящийся у его поверхности на расстоянии х электрон индуцирует в металле заряд е+ (рис.97). Этот наведенный заряд действует на вышедший электрон так, как если бы он был сосредоточен под поверхностью металла на глубине х в точке, симметричной той, в которой находится электрон (см. Эл-во §5). Индуцированный заряд е+ называется электрическим изображением заряда е-. Оба точечные заряда притягиваются друг к другу с силой Кулона . (14.1)
Но это и есть сила притяжения металлом вышедшего из него электрона. Под действием этой силы электрон втягивается обратно в металл. Чтобы удалить электрон из металла, надо совершить работу по преодолению этой силы, перемещая электроны на бесконечность из точки, расположенной на расстоянии х0 от поверхности металла. В качестве х0 можно взять межатомное расстояние.
На рис.98 показана зависимость потенциальной энергии электрона от расстояния х до атомной плоскости – стенки металла. Энергетическое расстояние еj от уровня Ферми до нулевого уровня называют термодинамической работой выхода электрона, величину j – потенциалом выхода. Уровень Ес обозначает дно зоны проводимости, где Е = 0. У металлов работа выхода еj заключена в пределах 1,8 ¸ 5,3 эВ. Меньше всего она у щелочных металлов, больше – у золота, серебра, платины (табл. 14.1).
| Таблица 14.1 | |||
| Металл | еj, эВ | Металл | еj, эВ |
| Литий Li | 2,38 | Платина Pt | 5,32 |
| Натрий Na | 2,35 | Ванадий V | 4,58 |
| Калий К | 2,22 | Вольфрам W | 4,54 |
| Рубидий Rb | 2,16 | Золото Au | 4,30 |
| Цезий Cs | 1,18 | Серебро Ag | 4,30 |
Большое влияние на работу выхода оказывают мономолекулярные адсорбированные слои. Например, слой атомов цезия Cs на вольфраме W (рис.99). Цезий щелочной металл. Его внешний, валентный электрон связан с ядром значительно слабее, чем валентные электроны в вольфраме. Поэтому атомы цезия отдают вольфраму свои валентные электроны и превращаются в положительные ионы. Между этими ионами и их электрическими изображениями в вольфраме возникает сила притяжения, удерживающая ионы цезия на поверхности вольфрама. Поле этого двойного электрического слоя помогает выходу электронов из вольфрама. По этому в присутствии слоя цезия работа выхода электрона из вольфрама уменьшается с 4,54 эВ до 1,38 эВ. Подобно цезию действуют одноатомные слои бария Ba, церия Cе, тория Th и др.
2. Термоэлектронная эмиссия.
С повышением температуры металла поверхность Ферми разрыхляется, энергия электронов увеличивается, и они поднимаются на более высокие уровни (рис.100). Соответственно уменьшается работа выхода электронов. Поэтому концентрация вылетевших из кристалла электронов в пристеночном слое растет. Процесс испускания электронов нагретым металлом называется термоэлектронной эмиссией.
Формально термоэлектронная эмиссия есть всегда, когда Т > 0 К. Но заметной она становится при температурах Т > 800 К.
Облако термоэлектронов находится в динамическом равновесии. Число вылетевших из металла электронов в каждый промежуток времени примерно равно числу электронов, втянутых в металл. Поэтому суммарный ток эмиссии равен нулю.
На основе термоэлектронной эмиссии построен ламповый вакуумный диод (рис.101). Здесь К – катод, обычно нагреваемая вольфрамовая спираль, А – анод, холодная металлическая пластина обычно цилиндрической формы. По оси этого цилиндра натягивается спираль катода. Оба электрода помещаются в стеклянный сосуд с высоким вакуумом.
Если между катодом и анодом создавать электрическое поле с напряжением U, как показано на рис.101, то термоэлектроны под действием этого поля будут перемещаться от катода к аноду. Возникает электрический ток в вакууме. Вольтамперная характеристика вакуумного диода показана на рис.102. С повышением анодного напряжения U ток I через анод растет почти пропорционально U. Но при достижении некоторого значенья Iнас перестает увеличиваться. Это предельное значение Iнас называют ток насыщением. Он возникает тогда, когда все электроны, вылетевшие из нагретого катода, захватываются полем и переносятся к аноду.
С повышением температуры катода ток насыщения увеличивается. Разделив ток насыщения на поверхность S катода, получаем плотность тока насыщения jнас = iнасçS. В 1901г. Оуэн Ричардсон, исходя из классических представлений, теоретически нашел зависимость плотности тока насыщения от температуры поверхности катода. Уточненная Дешманом в 1923г. с учетом квантовых представлений, зависимость jнас(Т) имеет вид: . Формула Ричардсона-Дэшмана (14.2)
Здесь еj – работа выхода, А – константа, имеющая разное значение у разных металлов и колеблющаяся около теоретического значения А= 1,2·10 6 Аç(м 2 К 2 ).
3. Контактная разность потенциалов.
Рассмотрим процессы, происходящие при контакте двух разных металлов. Допустим, до электрического контакта металл 1 (на рис.103 слева) имеет работу выхода еj1, а работа выхода металла 2 больше, j2 > j1.
Приведем металлы в состояние электрического контакта, то есть сблизим их до такого расстояния, при котором возможен эффективный обмен электронами. Поскольку работа выхода электронов из металла 2 больше, то уровень Ферми в металле 2 ниже, чем в металле 1. В результате электроны проводимости с уровня Ферми металла 1 начинают переходить на уровень Ферми металла 2.
В результате такого перехода электронов металл 2 заряжается отрицательно, энергия электронов и, соответственно, уровень Ферми в нем повышаются. Металл 1 заряжается положительно, энергия электронов и уровень Ферми в нем понижаются. Между металлами возникает контактная разность потенциалов j12.
Суммарное перетекание зарядов прекратится, когда уровни Ферми сравняются, а разность потенциалов между проводниками будет равна разности потенциалов выхода, j12 = j2 - j1, и встречные потоки электронов сравняются n21=-n12 (рис.103 справа). Контактная разность потенциалов между проводниками создает для электронов, переходящих в проводник с большей работой выхода, потенциальный барьер высотой еj12.
Оценим количество электронов, перетекающих из одного металла в другой при возникновении контактной разности потенциалов j12. Будем считать, что между контактирующими металлами остается зазор шириной d, а заряды концентрируются на контактирующих поверхностях. Тогда заряд Q на каждой из поверхностей, необходимый для создания напряжения j12, найдется из формулы плоского конденсатора, . (14.3)
Как видно из таблицы 14.1, контактная разность потенциалов В. Расстояние d между металлами не может быть меньше параметра решетки а » 0,3 нм. Полагая j12 =1 В и d = 0,3 нм, получаем максимальную плотность заряда на контактирующих поверхностях.
Разделив на заряд электрона получаем, что на 1 м 2 поверхности приходится 2·10 17 электронов. Если диаметр атомов взять равным постоянной решетки а = 0,3 нм, то на 1 м 2 поверхности в одноатомном слое металла размещается атомов. Если атомы металла содержат по одному валентному электрону, то для создания контактной разности потенциалов 1 В потребовалось всего лишь (2×10 17 ç10 19 )´100% = 2% электронов проводимости одноатомного поверхностного слоя.
4. Закон Вольта.
Контактную разность потенциалов открыл в девяностых годах XVIII века итальянец Александр Вольта. В серии экспериментов 1792–1794 годов он установил, что в цепочке из ряда последовательно соединенных металлов контактная разность потенциалов зависит лишь от крайних металлов. Этот опытный факт называется законом Вольта. Действительно, пусть имеется цепочка из металлов 1,2,3,4 (рис.104). Работа выхода металлов еj1, еj2, еj3, еj4. На границе каждой пары возникает контактная разность:
Просуммировав левые и правые части, получаем: . (14.5)
Сумма всех контактных ЭДС (левой части равенства) равна контактной ЭДС крайних металлов в цепочке (правая часть равенства). Если концы цепи замкнуть, то независимо от количества звенев сумма контактных разностей потенциалов равна нулю. Тока в цепи нет.
5. Термо-ЭДС.
Сумма контактных разностей потенциалов в замкнутой цепи равна нулю лишь при условии, что температуры всех контактов одинаковы. В 1821 г. Томас Зеебек, сжимая концы висмутовой и медной пластинок теплыми пальцами обнаружил, что если цепь замкнута, то в ней протекает ток. Это явление возникновения ЭДС в цепи из разных металлов при перепаде температур между спаями называют эффектом Зеебека или термоэлектричеством. В рамках классической электронной теории можно дать простое толкование явлению Зеебека и получить зависимость термо-ЭДС от перепада температур.
Пусть имеется замкнутая цепь из двух металлов 1 и 2 со спаями A и B (рис.105). Полагаем, что электроны проводимости на верхних уровнях зоны проводимости распределяются в силовом поле решетки по закону Больцмана.
Здесь n01 и n02 – концентрация электронов проводимости на уровнях Ферми. В силу полной заполняемости этих уровней будем полагать n01 = n02; U1 и U2 – потенциальная энергия электронов в металлах 1 и 2. Она может изменяться от нуля на уровне Ферми до еj (работа выхода) на нулевом уровне. Разделим первое уравнение на второе.
Разделив разность U1 –U2 на заряд электрона е, получаем концентрационную разность потенциалов между металлами 1 и 2. . (14.9)
Если температуры спаев ТА и ТB одинаковы, то концентрационная ЭДС в замкнутой цепи, так же, как контактная разность потенциалов, равна нулю. Тока в цепи нет. Если же температуры спаев разные, ТА ¹ ТB, то в цепи возникает термо-ЭДС (рис.106). Концентрационные перепады потенциалов в контактах А и B разные.
Учитывая грубость классических приближений, обычно выделяют лишь температурную зависимость, которая хорошо подтверждается опытом при малых перепадах температур, . (14.12)
Термо-ЭДС, возникающая в цепи из разных металлов, широко применяется для измерения температур в диапазоне от 0 К до » 1000°С. Соответствующее устройство из двух разных металлов называется термопарой. Один спай термопары поддерживается при постоянной температуре, например при 0 о С в сосуде с тающим льдом, другой помещают в ту среду, температуру которой хотят измерить. О величине температуры можно судить как по величине термотока, измеряемого гальванометром, так и более точно по величине термо-ЭДС, измеряемой методом компенсации. С помощью термопар можно измерять температуру с точностью до сотых долей градуса.
6. Эффект Пельтье,1834 г.
Он обратен эффекту Зеебека и состоит в том, что при пропускании тока по цепи из разных металлов один контакт у металла нагревается, другой охлаждается.
Пусть в цепи из двух разных металлов действует источник тока – батарея Б. В результате в цепи идет постоянный ток I (рис.107). Проходя спай B, электроны, идущие по цепи на рисунке против часовой стрелки, дополнительно ускоряются полем контактного потенциала. Их скорость дрейфа увеличивается, поэтому при столкновении с узлами электроны передают им большую, по сравнению со средней, энергию. Спай В нагревается больше, чем рядом расположенные участки проводников.
В спае А электроны тормозятся контактным полем, их скорость дрейфа уменьшается, поэтому спай А нагревается меньше, чем рядом расположенные участки проводов. Кроме того, для установления равновесия этих электронов с электронным газом им необходимо приобрести еще энергию. Эту энергию они черпают из решетки. В результате спай А охлаждается больше, чем нагревается. В итоге теплота в спае А поглощается.
Выделяющаяся или поглощающаяся теплота Пельтье QП в контакте пропорциональна заряду It, прошедшему через контакт. . (14.13)
Здесь П – коэффициент Пельтье связан с дифференциальной термо-ЭДС соотношением: П = аDT.(14.14)
Где DТ – разность температур между контактами.
Эффект Пельтье позволяет создавать малогабаритные холодильные устройства. Их особенность в том, что изменяя направление тока в цепи, можно один и тот же контакт заставить как поглощать тепло (холодильник), так и выделять его (нагреватель).
7. Эффект Томсона.
В 1853 – 54 г.г. Рудольф Клаузиус и Уильям Томсон независимо друг от друга применили к явлениям термоэлектричества принципы термодинамики. В процессе построения термодинамической теории термоэлектричества Томсон установил, что неравномерно нагретый проводник должен вести себя как система находящихся в контакте физически разнородных участков. На этом основании Томсон пришёл к заключению и подтвердил его экспериментально, что в однородном неравномерно нагретом проводнике должно выделяться или поглощаться тепло Пельтье (тепло Томсона). Само явление назвали эффектом Томсона.
Принципиальная схема экспериментальной установки изображена на рис.108
Концы двух одинаковых проводящих стержней помещены в два термостата с разными температурами Т1 и Т2. Допустим, Т1 > Т2. Тогда градиент температуры в верхнем стержне направлен по току I, а в нижнем – против тока. В результате в одном стержне выделяется тепло Томсона (его температура выше), а в другом – поглощается.
Знак эффекта у разных проводников разный. В висмуте и цинке, например, тепло выделяется, если поток тепла и электрический ток совпадают по направлению (на рисунке нижний проводник). А в Fe, Pt, Sb при тех же условиях тепло поглощается. С изменением направления тока знак эффекта во всех проводниках меняется.
Тепло Томсона Q, выделяющееся в проводнике, пропорционально перепаду температур ΔТ, току I, протекающему по проводнику, и времени t Q = σΔTIt.
Здесь σ – коэффициент Томсона. Он зависит от материала провода и от его температуры. Коэффициент σ невелик. У металлов он порядка 10 –5 ВçК. За положительное направление тока принимают направление градиента температур, то есть направление от холодного конца проводника к горячему. Если тепло при этих условиях выделяется (проводник нагревается), эффект Томсона считается положительным.
Количественно эффект Томсона исследовал в 1867 г. Франсуа Леру. В установке, собранной по схеме рис. 108, к поверхности стержней он присоединял спаи термопар. Пока тока через стержни не было, термоЭДС в цепи термопар была равна нулю. При включении тока через стержни появлялась термоЭДС, величина и знак которой позволяли определить коэффициент Томсона σ.
8. Закон Джоуля – Ленца в замкнутой цепи всегда выполняется. Суммарный эффект Пельтье и Томсона в замкнутой цепи равен нулю, поскольку наряду с участками цепи, где тепло Пельтье и Томсона выделяется, всегда есть участки, где такое же тепло поглощается.
Читайте также:
