Постоянный ток в металлах
Открытия, связанные с электричеством, кардинально изменили нашу жизнь. Используя электрический ток как источник энергии, человечество сделало прорыв в технологиях, которые облегчили наше существование. Сегодня электричество приводит в движение токарные станки, автомобили, управляет роботизированной техникой, обеспечивает связь. Этот список можно продолжать очень долго. Даже трудно назвать отрасль, где можно обойтись без электроэнергии.
В чём секрет такого массового использования электричества? Ведь в природе существуют и другие источники энергии, более дешевые, чем электричество. Оказывается всё дело в транспортировке.
Электрическую энергию можно доставить практически везде:
- к производственному цеху;
- квартире;
- на поле;
- в шахту, под воду и т. д.
Электроэнергию, накопленную аккумулятором, можно носить с собой. Мы пользуемся этим ежедневно, беря с собой сотовый телефон. Ни один другой вид энергии не обладает такими универсальными свойствами как электричество. Разве это не является достаточной причиной для того, чтобы глубже изучить природу и свойства электричества?
Что такое электрический ток?
Электрические явления наблюдались давно, но объяснить их природу человек смог относительно недавно. Удар молнии казался чем-то неестественным, необъяснимым. Странным казалось потрескивание некоторых предметов при их трении. Искрящаяся в темноте расчёска, после расчёсывания шерсти животных (например, кошки) вызвала недоумение, но подогревала интерес к этому явлению.
Как всё начиналось
Ещё древним грекам было известно свойство янтаря, потёртого о шерсть, притягивать некоторые мелкие предметы. Кстати, от греческого названия янтаря –«электрон» пошло название «электричество».
Когда физики вплотную занялись исследованием электризации тел, они начали понимать природу подобных явлений. А первый кратковременный электрический ток, созданный человеком, появился при соединении проводником двух наэлектризованных предметов (см. рис. 1). В 1729 году англичане Грей и Уиллер открыли проводимость зарядов некоторыми материалами. Но определения электрического тока они не смогли дать, хотя и понимали, что заряды перемещаются от одного тела к другому по проводнику.

Рис. 1. Опыт с заряженными телами
Об электрическом токе, как о физическом явлении заговорили лишь после того, как итальянец Вольта дал объяснение опытам Гальвани, а в 1794 году изобрёл первый в мире источник электричества – гальванический элемент (столб Вольта). Он обосновал упорядоченное перемещение заряженных частиц по замкнутой цепи.
Определение
В современной трактовке электрическим током называют направленное перемещение силами электрического поля заряженных частиц, Носителями зарядов металлических проводников являются электроны, а растворов кислот и солей – отрицательные и положительные ионы. Полупроводниковыми носителями зарядов являются электроны и «дырки».
Для того чтобы электрический ток существовал, необходимо всё время поддерживать электрическое поле. Должна существовать разница потенциалов, поддерживающая наличие первых двух условий. До тех пор, пока эти условия соблюдены, заряды будут упорядоченно перемещаться по участкам замкнутой электрической цепи. Эту задачу выполняют источники электричества.
Такие условия можно создать, например, с помощью электрофорной машины (рис. 2). Если два диска вращать в противоположных направлениях, то они будут заряжаться разноимёнными зарядами. На щётках, прилегающих к дискам, появится разница потенциалов. Соединив контакты проводником, мы заставим заряженные частицы двигаться упорядоченно. То есть электрофорная машина является источником электричества.

Рисунок 2. Электрофорная машина
Источники тока
Первыми источниками электрической энергии, нашедшими практическое применение, были упомянутые выше гальванические элементы. Усовершенствованные гальванические элементы (народное название – батарейки) широко применяются по сей день. Они используются для питания пультов управления, электронных часов, детских игрушек и многих других гаджетов.
С изобретением генераторов переменных токов электричество приобрело второе дыхание. Началась эра электрификации городов, а позже и всех населённых пунктов. Электрическая энергия стала доступной для всех граждан развитых стран.
Сегодня человечество ищет возобновляемые источники электроэнергии. Солнечные панели, ветряные электростанции уже занимают свои ниши в энергосистемах многих стран, включая Россию.
Характеристики
Электрический ток характеризуется величинами, которые описывают его свойства.
Сила и плотность тока
Для описания характеристики электричества часто используют термин «сила тока». Название не совсем удачное, так как оно характеризует только интенсивность движения электрических зарядов, а не какую-то силу в буквальном смысле. Тем не менее, этим термином пользуются, и он означает количество электричества (зарядов) проходящего через плоскость поперечного сечения проводника. Единицей измерения силы тока в системе СИ является ампер (А).
1 А означает то, что за одну секунду через поперечное сечение проводника проходит электрический заряд 1 Кл. (1А = 1 Кл/с).
Плотность тока – векторная величина. Вектор направлен в сторону движения положительных зарядов. Модуль этого вектора равен отношению силы тока на некотором перпендикулярном к направлению движения зарядов сечении проводника к площади этого сечения. В системе СИ измеряется в А/м 2 . Плотность более ёмко характеризует электричество, однако на практике чаще используется величина «сила тока».
Разница потенциалов (напряжение) на участке цепи выражается соотношением: U = I×R, где U – напряжение, I – сила тока, а R – сопротивление. Это знаменитый закон Ома для участка цепи.
Мощность
Электрическими силами совершается работа против активного и реактивного сопротивления. На пассивных сопротивлениях работа преобразуется в тепловую энергию. Мощностью называют работу, выполненную за единицу времени. По отношению к электричеству применяют термин «мощность тепловых потерь». Физики Джоуль и Ленц доказали, что мощность тепловых потерь проводника равна силе тока умноженной на напряжение: P = I× U. Единица измерения мощности – ватт (Вт).
Частота
Переменный ток характеризуется также частотой. Данная характеристика показывает, как за единицу времени изменяется количество периодов (колебаний). Единицей измерения частоты является герц. 1 Гц = 1 периоду за секунду. Стандартная частота промышленного тока составляет 50 Гц.
Ток смещения
Понятие «ток смещения» ввели для удобства, хотя в классическом понимании его нельзя назвать током, так как отсутствует перенос заряда. С другой стороны, интенсивность магнитного поля пребывает в зависимости от токов проводимости и смещения.
Токи смещения можно наблюдать в конденсаторах. Несмотря на то, что при зарядке и разрядке между обкладками конденсатора не происходит перемещения заряда, ток смещения протекает через конденсатор и замыкает электрическую цепь.
Виды тока
По способу генерации и свойствам электроток бывает постоянным и переменным. Постоянный – это такой, что не меняет своего направления. Он течёт всегда в одну сторону. Переменный ток периодически меняет направление. Под переменным понимают любой ток, кроме постоянного. Если мгновенные значения повторяются в неизменной последовательности через равные промежутки времени, то такой электроток называют периодическим.
Классификация переменного тока
Классифицировать изменяющиеся во времени токи можно следующим образом:
- Синусоидальный, подчиняющийся синусоидальной функции во времени.
- квазистационарный – переменный, медленно изменяющийся во времени. Обычные промышленные токи являются квазистационарными.
- Высокочастотный – частота которого превышает десятки кГц.
- Пульсирующий – импульс которого периодически изменяется.
Различают также вихревые токи, которые возникают в проводнике при изменении магнитного потока. Блуждающие токи Фуко, как их ещё называют, не текут по проводам, а образуют вихревые контуры. Индукционный ток имеет ту же природу что и вихревой.
Дрейфовая скорость электронов
Электричество по металлическому проводнику распространяется со скоростью света. Но это не означает, что заряженные частицы несутся от полюса к полюсу с такой же скоростью. Электроны в металлических проводниках встречают на своём пути сопротивление атомов, поэтому их реальное перемещение составляет всего 0,1 мм за секунду. Реальная, упорядоченная скорость перемещения электронов в проводнике называется дрейфовой.
Если замкнуть проводником полюсы источника питания, то вокруг проводника молниеносно образуется электрическое поле. Чем больше ЭДС источников, тем сильнее проявляется напряжённость электрического поля. Реагируя на напряжённость, заряженные частицы вмиг принимают упорядоченное движение и начинают дрейфовать.
Направление электрического тока
Традиционно считают, что вектор электрического тока направлен к отрицательному полюсу источника. Но на самом деле электроны движутся к положительному полюсу. Традиция возникла из-за того, что за направление вектора было выбрано движение положительных ионов в электролитах, которые действительно стремятся к негативному полюсу.
Электроны проводимости с отрицательным зарядом в металлах были открыты позже, но физики не стали менять первоначальные убеждения. Так укрепилось утверждение, что ток направлен от плюса к минусу.
Электрический ток в различных средах
В металлах
Носителями тока в металлических проводниках являются свободные электроны, которые из-за слабых электрических связей хаотично блуждают внутри кристаллических решёток (рис. 3). Как только в проводнике появляется ЭДС, электроны начинают упорядочено дрейфовать в сторону позитивного полюса источника питания.

Рис. 3. Электрический ток в металлах
В результате прохождения тока возникает сопротивление проводников, которое препятствует потоку электронов и приводит нагреванию. При коротком замыкании выделение тепла настолько сильное, разрушает проводник.
В полупроводниках
В обычном состоянии у полупроводника нет свободных носителей зарядов. Но если соединить два разных типа полупроводников, то при прямом подключении они превращаются в проводник. Происходит это потому, что у одного типа есть положительно заряженные ионы (дырки), а у другого – отрицательные ионы (атомы с лишним электроном).
Под напряжением электроны из одного полупроводника устремляются для замещения (рекомбинации) дырок в другом. Возникает упорядоченное движение свободных зарядов. Такую проводимость называют электронно-дырочной.
В вакууме и газе
Электрический ток возможен и в ионизированном газе. Заряд переносится положительными и отрицательными ионами. Ионизация газов возможна под действием излучения или вследствие сильного нагревания. Под действием этих факторов возбуждаются атомы, которые превращаются в ионы (рис. 4).

Рис 4. Электрический ток в газах
В вакууме электрические заряды не встречают сопротивления, поэтому. заряженные частицы движутся с околосветовыми скоростями. Носителями зарядов являются электроны. Для возникновения тока в вакууме необходимо создать источник электронов и достаточно большой положительный потенциал на электроде.
Примером может служить работа вакуумной лампы или электронно-лучевая трубка.
В жидкостях
Оговоримся сразу – не все жидкости являются проводниками. Электрический ток возможен в кислотных, щёлочных и соляных растворах. Иначе говоря – в средах, где имеются заряженные ионы.
Если опустить в раствор два электрода и подключить их к полюсам источника, то между ними будет протекать электрический ток (рис. 5). Под действием ЭДС катионы устремятся к катоду (минусу), а анионы к аноду. При этом будет происходить химическое воздействие на электроды – на них будут оседать атомы растворённых веществ. Такое явление называют электролизом.
Для лучшего понимания свойств электротока в разных средах, предлагаю рассмотреть картинку на рисунке 6. Обратите внимание на вольтамперные характеристики (4 столбец).
Рис. 6. Электрический ток в средах
Проводники электрического тока
Среди множества веществ, лишь некоторые являются проводниками. К хорошим проводникам относятся металлы. Важной характеристикой проводника является его удельное сопротивление.
Небольшое сопротивление имеют:
- все благородные металлы;
- медь;
- алюминий;
- олово;
- свинец.
На практике наиболее часто применяют алюминиевые и медные проводники, так как они не слишком дорогие.
Электробезопасность
Несмотря на то что электричество прочно вошло в нашу жизнь, не следует забывать об электробезопасности. Высокие напряжения опасны для жизни, а короткие замыкания становятся причиной пожаров.
При выполнении ремонтных работ необходимо строго соблюдать правила безопасности: не работать под высоким напряжением, использовать защитную одежду и специальные инструменты, применять ножи заземления и т.п.
В быту используйте только такую электротехнику, которая рассчитана на работу в соответствующей сети. Никогда не ставьте «жучки» вместо предохранителей.
Помните, что мощные электролитические конденсаторы имеют большую электрическую емкость. Накопленная в них энергия может вызвать поражение даже спустя несколько минут после отключения от сети.
Электрический ток в металлах
Электрическим током в металлах называют упорядоченное движение электронов под действием электрического поля.
Исходя из опытов, видно, что металлический проводник вещество не переносит, то есть ионы металла не участвуют в передвижении электрического заряда.
Носители тока в металлах
При исследованиях были получены доказательства электронной природы тока в металлах. Еще в 1913 году Л.И. Мандельштам и Н.Д. Папалекси выдали первые качественные результаты. А в 1916 году Р. Толмен и Б. Стюарт модернизировали имеющуюся методику и выполнили количественные измерения, которые доказывали, что движение электронов происходит под действием тока в металлических проводниках.
Рисунок 1 . 12 . 1 показывает схему Толмена и Стюарта. Катушка, состоящая из большого количества витков тонкой проволоки, приводилась в действие при помощи вращения вокруг своей оси. Ее концы были прикреплены к баллистическому гальванометру Г. Производилось резкое торможение катушки, что было следствием возникновения кратковременного тока, обусловленного инерцией носителя заряда. Измерение полного заряда производилось при помощи движения стрелок гальванометра.
Рисунок 1 . 12 . 1 . Схема опыта Толмена и Стюарта.
Во время торможения вращающейся катушки сила F = - m d υ d t , называемая тормозящей, действовала на каждый носитель заряда е . F играла роль сторонней силы, иначе говоря, неэлектрического происхождения. Именно эта сила, характеризующаяся единицей заряда, является напряженностью поля сторонних сил E с т :
E с т = - m e d υ d t .
То есть при торможении катушки происходит возникновение электродвижущей силы δ , равной δ = E с т l = m e d υ d t l , где l – длина проволоки катушки. Определенный промежуток времени процесса торможения катушки обусловлен протеканием по цепи заряда q :
q = ∫ I d t = 1 R ∫ δ d t = m e l υ 0 R .
Данная формула объясняет, что l – это мгновенное значение силы тока в катушке, R – полное сопротивление цепи, υ 0 – начальная линейная скорость проволоки. Видно, что определение удельного заряда e m в металлах производится, исходя из формулы:
Величины, находящиеся с правой стороны, можно измерить. Основываясь на результатах опытов Толмена и Стюарта, установили, что носители свободного заряда имеют отрицательный знак, а отношение носителя в его массе близко по значению удельного заряда электрона, получаемого в других опытах. Было выявлено, что электроны – это носители свободных зарядов.
Современные данные показывают, что модуль заряда электрона, то есть элементарный заряд, равняется e = 1 , 60218 · 10 - 19 К л , а обозначение его удельного заряда – e m = 1 , 75882 · 10 11 К л / к г .
При наличии отличной концентрации свободных электронов есть смысл говорить о хорошей электропроводимости металлов. Это выявили еще перед опытами Толмена и Стюарта. В 1900 году П. Друде, основываясь на гипотезе о существовании свободных электронов в металлах, создал электронную теорию проводимости металлов. Ее развил и расширил Х. Лоренц, после чего она получила название классическая электронная теория. На ее основании поняли, что электроны ведут себя как электронный газ, похожий на идеальный по своему состоянию. Рисунок 1 . 12 . 2 показывает, каким образом он может заполнить пространство между ионами, которые уже образовали кристаллическую решетку металла.
Рисунок 1 . 12 . 2 . Газ свободных электронов в кристаллической решетке металла. Показана траектория одного из электронов.
Потенциальный барьер. Движение электронов в кристаллической решетке
После взаимодействия электронов с ионами первые покидают металл, преодолевая только потенциальный барьер.
Высота такого барьера получила название работы выхода.
Наличие комнатной температуры не позволяет электронам проходить этот барьер. Потенциальная энергия выхода электрона после взаимодействия с кристаллической решеткой намного меньше, чем при удалении электрона из проводника.
Расположение е в проводнике характеризуется наличием потенциальной ямы, глубина которой получила название потенциального барьера.
Ионы, образующие решетку, и электроны принимают участие в тепловом движении. Благодаря тепловым колебаниям ионов вблизи положений равновесий и хаотичному движению свободных электронов, при столкновении первых со вторыми происходит усиление термодинамического равновесия между электронами и решеткой.
По теории Друде-Лоренца имеем, что электроны имеют такую же среднюю энергию теплового движения, как и молекулы одноатомного идеального газа. Это делает возможным оценивание средней скорости υ т ¯ теплового движения электронов, используя молекулярно-кинетическую теорию.
Комнатная температура дает значение, равное 10 5 м / с .
Если наложить внешнее электрическое поле в металлический проводник, тогда произойдет тепловое упорядоченное движения электронов (электрический ток), то есть дрейф. Определение средней его скорости υ д ¯ выполняется по интервалу имеющегося времени ∆ t через поперечное сечение S проводника электронов, которые находятся в объеме S υ д ∆ t .
Количество таких е равняется n S υ д ∆ t , где n принимает значение средней концентрации свободных электронов, равняющейся числу атомов в единице объема металлического проводника. За имеющееся количество времени ∆ t через сечение проводника проходит заряд ∆ q = e n S υ д ∆ t .
Тогда I = ∆ q ∆ t = e n S υ д или υ д = I e n S .
Концентрация n атомов в металлах находится в пределах 10 28 - 10 29 м - 3 .
Формула дает возможность оценить среднюю скорость υ д ¯ упорядоченного движения электронов со значением в промежутке 0 , 6 - 6 м м / с для проводника с сечением 1 м м 2 и проходящим током в 10 А .
Средняя скорость υ д ¯ упорядоченного движения электронов в металлических проводниках на много порядков меньше скорости υ т их теплового движения υ д ≪ υ т .
Рисунок 1 . 12 . 3 демонстрирует характер движения свободного е , находящегося в кристаллической решетке.
Рисунок 1 . 12 . 3 . Движение свободного электрона в кристаллической решетке: а – хаотическое движение электрона в кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным электрическим полем. Масштабы дрейфа υ д ¯ ∆ t сильно преувеличены.
Наличие малой скорости дрейфа не соответствует опыту, когда ток всей цепи постоянного тока устанавливается мгновенно. Замыкание производится при помощи воздействия электрического поля со скоростью c = 3 · 10 8 м / с . По прошествии времени l c ( l - длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля. В ней происходит упорядоченное движение электронов.
Классическая электронная теория металлов предполагает, что их движение подчинено законам механики Ньютона. Данная теория характеризуется тем, что происходит пренебрежение взаимодействием электронов между собой, а взаимодействие с положительными ионами расценивается как соударения, при каждом из которых e сообщает накопленную энергию решетке. Поэтому принято считать, что после соударения движение электрона характеризуется нулевой дрейфовой скоростью.
Абсолютно все выше предложенные допущения приближенные. Это дает возможность объяснения законов электрического тока в металлических проводниках, основываясь на электронной классической теории.
Закон Ома
В промежутке между соударениями на электрон действует сила, равняющаяся по модулю e E , в результате чего получает ускорение e m E .
Конец свободного пробега характеризуется дрейфовой скоростью электрона, которую определяют по формуле
υ д = υ д m a x = e E m τ .
Время свободного пробега обозначается τ . Оно способствует упрощению расчетов для нахождения значения всех электронов. Средняя скорость дрейфа υ д равняется половине максимального значения:
υ д = 1 2 υ д m a x = 1 2 e E m τ .
Если имеется проводник с длиной l , сечением S с концентрацией электронов n , тогда запись нахождения тока в проводнике имеет вид:
I = e n S υ д = 1 2 e 2 τ n S m E = e 2 τ n S 2 m l U .
U = E l – это напряжение на концах проводника. Формула выражает закон Ома для металлического проводника. Тогда электрическое сопротивление необходимо находить:
R = 2 m e 2 n τ l S .
Удельное сопротивление ρ и удельная проводимость ν выражаются как:
ρ = 2 m e 2 n τ ; ν = 1 ρ = e 2 n τ 2 m .
Закон Джоуля-Ленца
Конец пробега электронов под действием поля характеризуется кинетической энергией
1 2 m ( υ д ) m a x 2 = 1 2 e 2 τ 2 m E 2 .
Исходя из предположений, энергия при соударениях передается решетке, а в последствии переходит в тепло.
Время ∆ t каждого электрона испытывается ∆ t τ соударений. Проводник с сечение S и длиной l имеет n S l электронов. Тогда выделившееся тепло в проводнике за ∆ t равняется
∆ Q = n S l ∆ t τ e 2 τ 2 2 m E 2 = n e 2 τ 2 m S l U 2 ∆ t = U 2 R ∆ t .
Данное соотношение выражает закон Джоуля-Ленца.
Благодаря классической теории, имеет место трактовка существования электрического сопротивления металлов, то есть законы Ома и Джоуля-Ленца. Классическая электронная теория не в состоянии ответить на все вопросы.
Она не способна объяснить разницу в значении молярной теплоемкости металлов и диэлектрических кристаллов, равняющейся 3 R , где R записывается как универсальная газовая постоянная. Теплоемкость металла не зависит от количества свободных электронов.
Классическая электронная теория не объясняет температурную зависимость удельного сопротивления металлов. По теории ρ ~ T , а исходя из экспериментов – ρ ~ T . Примером расхождения теории с практикой служит сверхпроводимость.
Сопротивление металлического проводника
Исходя из классической теории, удельное сопротивление металлов должно постепенно уменьшаться при понижении температуры, причем остается конечным при любой T . Данная зависимость характерна для проведения опытов при высоких температурах. Если T достаточно низкая, тогда удельное сопротивление металлов теряет зависимость от температуры и достигает предельного значения.
Особый интерес представило явление сверхпроводимости. В 1911 году его открыл Х. Каммерлинг-Оннес.
Если имеется определенная температура T к р , различная для разных веществ, тогда удельное сопротивление уменьшается до нуля с помощью скачка, как изображено на рисунке 1 . 12 . 4 .
Критической температурой для ртути считается значение 4 , 1 К , для алюминия – 1 , 2 К , для олова – 3 , 7 К . Наличие сверхпроводимости может быть не только у элементов, но и у химических соединений и сплавов. Ниобий с оловом Ni 3 Sn имеют критическую точку температуры в 18 К . Существуют вещества, которые при низкой температуре переходят в сверхпроводящее состояние, тогда как в обычных условиях ими не являются. Серебро и медь являются проводниками, но при понижении температуры сверхпроводниками не становятся.
Рисунок 1 . 12 . 4 . Зависимость удельного сопротивления ρ от абсолютной температуры T при низких температурах: a – нормальный металл; b – сверхпроводник.
Сверхпроводящее состояние говорит об исключительных свойствах вещества. Одним из важнейших является способность на протяжении длительного времени поддерживать электрический ток, возбужденный в сверхпроводящей цепи, без затухания.
Классическая электронная теория не может объяснить сверхпроводимость. Это стало возможным спустя 60 лет после его открытия, основываясь на квантово-механических представлениях.
Рост интереса к данному явлению увеличивался по мере появления новых материалов, способных обладать высокими критическими температурами. В 1986 было обнаружено сложное соединение с температурой T к р = 35 К . На следующий год сумели создать керамику с критической Т в 98 К , которая превышала Т жидкого азота ( 77 К ) .
Явление перехода веществ в сверхпроводящее состояние при Т , превышающих температуру кипения жидкого азота, называют высокотемпературной сверхпроводимостью.
Позже в 1988 году создали Tl - Ca - Ba - Cu - O соединение с критической Т , достигающей 125 К . На данный момент ученые заинтересованы в поиске новых веществ с наиболее высокими значениями T к р . Они рассчитывают на получение сверхпроводящего вещества при комнатной температуре. Если это будет сделано, произойдет революция в науке и технике. До настоящего времени все свойства и механизмы состава сверхпроводимых керамических материалов до конца не исследованы.
Постоянный электрический ток: определение, механизм, характеристики
Постоянный ток – это упорядоченное движение заряженных частиц, движущихся в одном направлении.
По теории данные заряженные частицы относят к носителям тока. В проводниках и полупроводниках такими носителями являются электроны, в электролитах – заряженные ионы, в газах – электроны и ионы. Металлы характеризуются перемещением только электронов. Отсюда следует, что электрический ток в них – это движение электронов проводимости.
Результат прохождения электрического тока в металлах и электропроводящих растворах заметно отличается. Наличие химических процессов в металлах при протекании тока отсутствует. В электролитах под воздействием тока происходит выделение ионов вещества на электродах. Различие заключается в отличии носителей зарядов металла и электролита. В металлах – это свободные электроны, отделившиеся от атомов, в растворах – ионы, атомы или их группы с зарядами.
Необходимые условия существования электрического тока
Первое необходимое условие существования электрического тока любого вещества – наличие носителей заряда.
Для равновесного состояния зарядов необходимо равнение нулю разности потенциалов между любыми точками проводника. При нарушении данного условия, заряд не сможет переместиться. Отсюда следует, что второе необходимое условие существования электрического тока в проводнике – создание напряжения между некоторыми точками.
Упорядоченное движение свободных зарядов, возникающее в проводнике как результат воздействия электрического поля, называют током проводимости.
Такое движение возможно при перемещении в пространстве заряженного проводника или диэлектрика. Подобный электрический ток получил название конвекционного.
Механизм осуществления постоянного тока
Для постоянного прохождения тока в проводнике следует подсоединить к проводнику или их совокупности устройство, в котором постоянно происходит процесс разделения электрических зарядов для поддержания напряжения в цепи. Данный механизм получил название источника тока (генератора).
Силы, разделяющие заряды, называют сторонними. Они характеризуются неэлектрическим происхождением, действуют внутри источника. При разделении зарядов сторонние силы способны создать разность потенциалов между концами цепи.
Если электрический заряд перемещается по замкнутой цепи, то работа электростатических сил равняется нулю. Отсюда следует, что суммарная работа сил A , действующих на заряд, равна работе сторонних A s t . Определение физической величины, характеризующей источник тока, ЭДС источника ε запишется как:
ε = A q ( 1 ) , где значение q подразумевает положительный заряд. Его движение происходит по замкнутому контуру. ЭДС – это не сила. Единица измерения ε = В .
Природа сторонних сил различна. В гальваническом элементе они являются результатом электрохимических процессов. В машине с постоянным током такой силой является сила Лоренца.
Основные характеристики электрического тока
Условно принято считать направление тока за направление движения положительных частиц. Отсюда следует, что направление тока в металлах характеризуется противоположным направлением относительно направления движения частиц.
Электрический ток обладает силой тока.
Сила тока I – скалярная величина, равняется производной от заряда q по времени для тока, который проходит через поверхность S :
Ток может быть постоянным и переменным. При неизменной силе тока с его направлением по времени ток называют постоянным, а выражение силы тока для него примет вид:
I = q t ( 3 ) , где сила тока рассматривается в качестве заряда, проходящего через поверхность S в единицу времени.
По системе С И основная единица измерения силы тока – Ампер ( А ) .
Плотность – это векторная локальная характеристика. Вектор плотности тока j → способен показывать, каким образом распределяется ток по сечению S . Его направление идет в сторону, куда движутся положительные заряды.
Значение вектора плотности тока по модулю равно:
j = d I d S ' ( 4 ) , где d S ' является проекцией элементарной поверхности d S на плоскость, перпендикулярную вектору плотности тока, d I – элементом силы, которая идет через поверхности d S и d S ' .
Представление плотности в металле возможно по формуле:
j → = - n 0 q e υ → ( 5 ) , где n 0 обозначается концентрацией электронов проводимости, q e = 1 , 6 · 10 - 19 К л – зарядом электрона, υ → – средней скоростью упорядоченного движения электронов. Если значение плотностей тока максимальное, то
Закон сохранения заряда
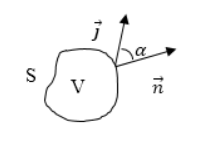
Основным физическим законом считается закон сохранения электрического заряда. При выборе произвольной замкнутой поверхности S , изображенной на рисунке 1 , ограничивающей объем V количество выходящего электричества в единицу времени ( 1 секунду) из объема V можно определить по формуле ∮ s j n d S . Такое же количество электричества выражается через заряд - ∂ q ∂ t , тогда получаем:
∂ q ∂ t = - ∮ S j n d S ( 6 ) , где j n считается проекцией вектора плотности на направление нормали к элементу поверхности d S , при этом:
j n = j cos a ( 7 ) , где a является углом между направлением нормали к d S и вектором плотности тока. Уравнение ( 6 ) показывает частое употребление производной для того, чтобы сделать акцент на неподвижности поверхности S .
Выражение ( 6 ) считается законом сохранения электрического заряда в макроскопической электродинамике. Если ток постоянен во времени, тогда запись этого закона примет вид:
∮ S j n d S = 0 ( 8 ) .
Найти формулу для того, чтобы рассчитать конвекционный ток при его возникновении в длинном цилиндре с радиусом сечения R и наличием его равномерной скорости движения υ , который заряжен по поверхности равномерно. Значение напряженности поля у поверхности цилиндра равняется E . Направление скорости движения вдоль оси цилиндра.
Решение
Основой решения задачи берется определение силы тока в виде:
I = d q d t ( 1 . 1 ) .
Из формулы ( 1 . 1 ) следует, что возможно нахождение элемента заряда, располагающегося на поверхности цилиндра.
Напряженность поля равномерно заряженного цилиндра на его поверхности находится по выражению:
E = σ ε 0 ( 1 . 2 ) , где σ является поверхностной плотностью заряда, ε 0 = 8 , 85 · 10 - 12 К л Н · м 2 . Выразим σ из ( 1 . 2 ) , тогда:
σ = E · ε 0 ( 1 . 3 ) .
Связь поверхностной плотности заряда с элементарным зарядом выражается при помощи формулы:
d q d S = σ ( 1 . 4 ) .
Используя ( 1 . 3 ) , ( 1 . 4 ) , имеем:
d q = E · e 0 d S ( 1 . 5 ) .
Выражение элемента поверхности цилиндра идет через его параметры:
d S = 2 π · R d h ( 1 . 6 ) , где d h является элементом высоты цилиндра. Запись элемента заряда поверхности цилиндра примет вид:
d q = E · ε 0 · 2 h · R d h ( 1 . 7 ) .
Произведем подстановку из ( 1 . 7 ) в ( 1 . 1 ) :
I = d ( E · ε 0 · 2 π · Rdh ) d t = 2 πRε 0 E dh dt ( 1 . 8 ) .
Движение цилиндра идет вдоль оси, тогда запишем:
d h d t = υ ( 1 . 9 ) .
I = 2 π R ε 0 E υ .
Ответ: конвективный ток I = 2 π R ε 0 E υ .
Изменение тока в проводнике происходит согласно закону I = 1 + 3 t . Определить значение заряда, проходящего через поперечное сечение проводника, за время t , изменяющегося от t 1 = 3 с до t 2 = 7 c . Каким должен быть постоянный электрический ток, чтобы за аналогичное время происходило то же значение заряда?
Основа решения задачи – выражение, связывающее силу тока и заряд, проходящий через поперечное сечение проводника:
I = d q d t ( 2 . 1 ) .
Формула ( 2 . 1 ) показывает, что нахождение количества заряда, проходящего через поперечное сечение проводника за время от t 1 до t 2 возможно таким образом:
q = ∫ t 1 t 2 I d t ( 2 . 2 ) .
Произведем подстановку имеющегося по условию закона в ( 2 . 2 ) для получения:
q = ∫ t 1 t 2 ( 1 + 3 t ) d t = ∫ t 1 t 2 d t + ∫ t 1 t 2 3 t d t = t 2 - t 1 + 3 · t 2 2 t 1 t 2 = ( t 2 - t 1 ) + 3 2 t 2 2 - t 1 2 ( 2 . 3 ) .
q = 7 - 3 + 3 2 ( 7 2 - 3 2 ) = 4 + 3 2 · 40 = 64 ( К л ) .
Чтобы определить постоянный ток для получения силы используется формула:
I c o n s t = q t ( 2 . 3 ) , где t считается временем, за которое поперечное сечение проводника пройдет заряд q .
Электрический ток в металлах: подробное объяснение
Электрический ток в металлах представляет собой упорядоченное движение свободных электронов. Более подробно об этом читайте далее в нашей статье.
Важно знать
Как известно, электрический ток – это упорядоченный поток носителей электрического заряда. Носители – это заряженные частицы, способные свободно перемещаться во всем объеме тела.
В случае металлов этими частицами являются электроны, которые высвобождаются при образовании связи между атомами металла.
Известно, что металлы в твердом состоянии имеют кристаллическую структуру. Частицы в кристаллах расположены в определенном порядке, образуя пространственную решетку (кристалл).
Наконец, кристаллическая решетка металла образована положительными ионами, погруженными в “облако” хаотически движущихся так называемых свободных электронов, также называемых электронами проводимости. В зависимости от валентности атомов металла, один атом может освободить от одного до трех электронов при образовании металлических связей. Число таких высвобожденных электронов непосредственно переводится в число носителей заряда. Это является одним из факторов, влияющих на способность металла проводить электрический ток.
Доказательством того, что ток в металлах вызывается электронами, послужили эксперименты наших отечественных физиков Леонида Исааковича Мандельштама и Николая Дмитриевича Папалекси, а также американских физиков Бальфура Стюарта и Роберта Толмана.
Способность металла проводить электрический ток может быть описана физической величиной, называемой удельным электрическим сопротивлением. Эта физическая величина обозначается греческой буквой ρ (читается как “ро”). Единицей измерения удельного сопротивления является Ом · м, т.е. произведение Ом на метр. Удельное сопротивление – это константа, которая характеризует материал и имеет различные значения для разных материалов. Например, удельное сопротивление меди составляет 1.72*10 -8 Ом · м. Это означает, что электрическое сопротивление медного проводника длиной 1 метр и площадью поперечного сечения 1 м равно 1.72*10 -8 Ом . В целом, чем ниже удельное сопротивление материала, тем лучше он проводит электрический ток.
В таблице ниже приведены некоторые примеры удельного сопротивления часто используемых металлов.
| Металл | Удельное сопротивление (Ом · м) |
| Серебро | 1.59*10 -8 |
| Медь | 1.72*10 -8 |
| Алюминий | 2.82*10 -8 |
| Вольфрам | 5.6*10 -8 |
| Железо | 10*10 -8 |
Удельное электрическое сопротивление может быть связано с микроскопическими свойствами материала. В частности, он зависит от концентрации носителей заряда и их подвижности.
Движение свободных электронов в металлах не является полностью “свободным”, поскольку во время их движении они взаимодействуют с другими электронами, и прежде всего с ионами кристаллической решетки. Специфика этого движения описывается так называемой классической моделью проводимости.
Основные предположения и выводы этой модели представлены в большом упрощении ниже.
Классическая модель проводимости
Без внешнего электрического поля электроны совершают тепловые хаотические движения, сталкиваясь друг с другом, а также сталкиваясь с ионами кристаллической решетки. В результате такого движения среднее положение электронов практически не меняется (см. рис. 1.).

Рис. 1. Пример траектории электрона во время его хаотического теплового движения в металле
Из-за квантовых эффектов, и в частности из-за принципа запрета Паули, который не позволяет всем электронам занимать самое низкое энергетическое состояние, средняя скорость электронов в металлах, связанная с их хаотическим тепловым движением, больше, чем скорость частиц в классическом идеальном газе той же температуры. Она составляет порядка 10 м/с.
Если электрическое напряжение U приложено к концам проводника длиной L в нем появится электрическое поле с напряженностью E = U / L
Под действием этого внешнего поля, согласно второму закону динамики, электроны ускоряются: a = F / m,
где F = e*E – сила, с которой электрическое поле действует на электрон с зарядом e. Таким образом, ускорение электрона составляет: a = e*E / m .
Ускоренное движение электрона длится лишь довольно короткое время, пока он не столкнется с ионом
кристаллической решетки. В результате такого столкновения электрон теряет практически всю свою кинетическую энергию. Однако замедленный электрон не остается в состоянии покоя – он снова ускоряется под действием электрического поля, снова сталкивается с одним из ионов из ионы кристаллической решетки и т.д. Этот эффект добавляет к скорости тепловых движений дополнительную направленную среднюю скорость u, которая из-за отрицательного заряда электрона имеет направление, противоположное напряженности внешнего электрического поля. Эта скорость называется средней скоростью дрейфа (рис. 2).

Рис. 2. Дрейф электрона под действием внешнего электрического поля
В проводнике начинает течь электрический ток с силой тока I (см. рисунок 3).

Рис. 3. Дрейфующие электроны сталкиваются с ионами кристаллической решетки
Предполагая, что движение электрона равномерно ускоряется между столкновениями с ионами решетки, с ускорением a = e*E / m , и предполагая, что в результате столкновения электрон передает всю свою кинетическую энергию кристаллической решетке, мы можем вычислить скорость, которую развивает электрон в своем свободном движении: v = a*τ . В этой формуле τ – средний интервал времени между последующими столкновениями дрейфующего электрона с ионами кристаллической решетки.
Поскольку при равномерно ускоренном движении без начальной скорости средняя скорость является средним арифметическим начальной (равной нулю) и конечной скоростью, то получаем: u = v / 2 = e*E*τ / 2*m .
Из полученной формулы следует, что скорость дрейфа, помимо внешнего электрического поля, определяется средним интервалом времени между столкновениями электронов с ионами решетки. Этот параметр зависит от многих факторов (включая температуру, кристаллическую структуру металла, дефекты кристаллической структуры, примеси) и, как выясняется, существенно влияет на электрическое сопротивление материала.
Средняя дрейфовая скорость электронов составляет порядка 10 -4 м/с. Она очень мала по сравнению со скоростью теплового движения, которая составляет порядка 10 6 м/с.
Классическая теория проводимости достаточно хорошо описывает явление электропроводности в металлах. Однако эта теория не может объяснить экспериментально наблюдаемую зависимость электрического сопротивления от температуры.
Причина упомянутой неудачи классической теории проводимости заключается в том, что она не учитывает влияние ионов решетки на движение электронов между столкновениями. Более близкие к реальности результаты дает квантовая теория проводимости, которая описывает электроны как частицы, подверженные квантовой статистике, движущиеся в периодическом электрическом поле, создаваемом положительными ионами решетки.
Выводы простым языком
Отрицательный заряд всех свободных электронов по абсолютному значению равен положительному заряду всех ионов решётки. Поэтому в обычных условиях металл электрически нейтрален. Свободные электроны в нём движутся беспорядочно. Но если в металле создать электрическое поле, то свободные электроны начнут двигаться направленно под действием электрических сил. Возникнет электрический ток. Беспорядочное движение электронов при этом сохраняется, подобно тому как сохраняется беспорядочное движение в стайке мошкары, когда под действием ветра она перемещается в одном направлении.
« Скорость движения самих электронов в проводнике под действием электрического поля невелика – несколько миллиметров в секунду, а иногда и ещё меньше. Но как только в проводнике возникает электрическое поле, оно с огромной скоростью, близкой к скорости света в вакууме (300 000 км/c), распространяетcя по всей длине проводника. »
Перышкин А. В. Физика 8. – М.: Дрофа, 2010
Как пример, электрический сигнал, посланный, например, по проводам из Москвы во Владивосток (s = 8000 км), приходит туда примерно через 0,03 с.
Одновременно с распространением электрического поля все электроны начинают двигаться в одном направлении по всей длине проводника. Так, например, когда цепь электрической лампы замкнута, электроны в спирали лампы также движутся упорядоченно.
Сравнение электрического тока с потоком воды в водопроводной системе и распространения электрического поля с распространением давления воды поможет нам понять это. Когда вода поднимается в резервуар для воды, давление (напор) воды очень быстро распространяется по всей системе водоснабжения. Когда мы включаем кран, вода уже находится под давлением и сразу же начинает течь. Но вода, которая была в кране, течет, а вода из башни достигает крана гораздо позже, потому что вода движется с меньшей скоростью, чем распространяется давление.
Когда говорят о скорости распространения электрического тока в проводнике, то имеют в виду скорость распространения по проводнику электрического поля.
Постоянный ток в металлах. Закон Ома и Джоуля-Ленца. Правила Кирхгофа.

Электрическим током называется всякое направленное движение электрических зарядов. Значит внутри проводника существует электрическое поле, характеризующееся напряженностью Е , которое вызывает и поддерживает упорядоченное движение зарядов.
Просмотр содержимого документа
«Постоянный ток в металлах. Закон Ома и Джоуля-Ленца. Правила Кирхгофа.»
Постоянный ток в металлах. Закон Ома и Джоуля-Ленца. Правила Кирхгофа.
Электрическим током называется всякое направленное движение электрических зарядов. Значит внутри проводника существует электрическое поле, характеризующееся напряженностью , которое вызывает и поддерживает упорядоченное движение зарядов. Поэтому между концами провода, несущего ток, должна существовать разность потенциалов U (напряжение или падение напряжения). Сила тока является функцией разности потенциалов
Основной характеристикой электрического тока является величина тока, численно равная количеству электричества, проходящего через поперечное сечение проводника в единицу времени
Если величина тока со временем не изменяется, то ток называется постоянным
I=Const. (5.2)
Электрический ток характеризуется различными действиями, которые не имеют места при покоящихся зарядах:
Прохождение электрического тока по проводнику приводит к нагреванию проводника - тепловое действие тока.
Магнитное действие тока впервые было открыто в 1820 г. Х.К. Эрстедом по отклонению магнитной стрелки, помещенной вблизи проводника с током.
В водных растворах неорганических кислот, солей и щелочей прохождение тока сопровождается химическими явлениями (выделение составных частей растворенного вещества - электролиз).
Тело человека, как и любой живой организм, является хорошим проводником электрического тока. Наибольшей проводимостью обладают нервные волокна; поэтому даже слабый ток является своеобразным "ударом" для нервной системы. Постоянный ток оказывает на ткани раздражающее действие, которое связано с изменением концентрации ионов в клетках и поляризационными процессами, что приводит к изменению распределения зарядов и, следовательно, функций. Слабые токи используются при физиологических исследованиях, для лечебных целей: восстановление проводимости нервов, сократительной способности мышц, восстановление костной ткани при переломах. Сильные электрические импульсы вызывают параличи, расстройство дыхания, кровообращения. Сильные электрические импульсы применяют для восстановления работы сердца после его остановки.
За единицу тока в системе СИ принимают величину такого постоянного тока, при котором через поперечное сечение проводника за одну секунду протекает 1 кулон электричества. Эту единицу называют ампером.
; 1мА = 10 -3 А; 1мкА = 10 -6 А.
Если концентрация (т.е. число частиц в единице объема) свободных электронов в данном проводнике n0, а скорость их направленного движения υ, то за время ∆t ( через поперечное сечение S переносится заряд
q = en0υ∆tS, (5.3)
где е - заряд электрона, тогда
I = en0υ∆tS. (5.4)
Величина тока для данного проводника пропорциональна скорости направленного перемещения электронов. Если ток постоянен, то и скорость электронов постоянна.
Плотностью тока называется величина, численно равная току, протекающему через единичную поверхность поперечного сечения проводника
Учитывая выражение (5.4), имеем
Плотность тока величина векторная, ее направление совпадает с вектором скорости направленного перемещения положительных зарядов в проводнике (в металлах направлено антипараллельно вектору скорости электронов).
Сопротивление однородного проводника длиной l, площадью поперечного сечения S выражается
где ρ - удельное сопротивление вещества. Величина, обратная удельному сопротивлению, называется удельной электрической проводимостью
а величина, обратная сопротивлению, называется проводимостью проводника
Наиболее просты законы электрического тока для металлов. Хорошо выполняется закон Ома для участка цепи
Найдем связь между вектором плотности тока и напряженности поля в некоторой точке проводника. В окрестности этой точки мысленно выделим малый цилиндр, ориентированный вдоль линий напряженности (рис. 5.1).
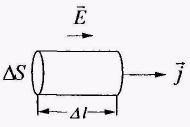
Н апряжение на длине ∆l цилиндра U = E∆l, сила тока через его сечение I = j∆S, а сопротивление цилиндра , подставив эти значения в закон Ома для участка цепи , получим
так как направления векторов и совпадают, то можно записать
- получили закон Ома в дифференциальной форме: плотность тока пропорциональна напряженности электрического поля и имеет одинаковое с ней направление.
Рассмотрим, какие силы действуют на свободный электрон в проводнике. С одной стороны, это кулоновские силы взаимодействия между зарядами. Но они всегда приводят к такому перераспределению зарядов, при котором наступает равновесие. Следовательно, кулоновские силы не могут вызвать длительный процесс упорядоченного движения зарядов, т.е. они не являются причиной постоянного электрического тока.
Для того, чтобы упорядоченное движение электрических зарядов все время поддерживалось, необходимо действие каких-либо иных, неэлектростатических сил. Такие силы получили название сторонних сил. Сторонние силы вызывают разделение электрических зарядов внутри источника тока (гальванических элементов, аккумуляторов, электрических генераторов).
За счет поля сторонних сил электрические заряды внутри источника тока движутся против сил электростатического поля, в результате чего на концах внешней цепи все время поддерживается определенная разность потенциалов и в цепи идет постоянный электрический ток.
Работа сторонних сил по перемещению электрических зарядов совершается за счет химической энергии в гальванических элементах и аккумуляторах или за счет механической работы, затрачиваемой на вращение ротора генератора. При этом особенностью сторонних сил является неравенство нулю циркуляции напряженности поля сторонних сил
Максимальная разность потенциалов развиваемая источником называется электродвижущей силой (ЭДС), которая измеряется в вольтах. При включении источника в цепь эта разность потенциалов длительно поддерживается постоянной и в цепи создается постоянный ток. Источник ЭДС обладает некоторым внутренним сопротивлением. Поэтому при протекании тока разность потенциалов на зажимах источника может уменьшиться на величину Ir, где r - внутреннее сопротивление источника.
ЭДС направлена от отрицательного полюса к положительному. В разомкнутом источнике электрическое напряжение уравновешивается ЭДС, т.е.
ЭДС - величина, измеряемая работой тока при перемещении единицы заряда по всей цепи
или ЭДС равна сумме падений напряжений на внешнем и внутреннем участках цепи.
ε = IR + Ir,
- закон Ома для замкнутой цепи. Закон Ома гласит: величина тока в замкнутой цепи прямо пропорциональна величине ЭДС, действующей в этой цепи, и обратно пропорциональна сумме внешнего и внутреннего сопротивлений.
При протекании тока в проводнике выделяется тепло
Q = UIt, (5.21)
так как по закону Ома U =IR, то можем записать
Q = RI 2 t. (5.22)
Это соотношение было установлено экспериментально Д.П. Джоулем и независимо от него Э. X. Ленцем и носит название закона Джоуля-Ленца.
Если сила тока изменяется со временем, то количество теплоты, выделяющееся за время t, вычисляется по формуле
- интегральная форма закона Джоуля-Ленца.
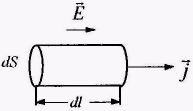
В ыделим в проводнике элементарный объем в виде цилиндра (рис. 5.2). Согласно закону Джоуля-Ленца за время dt в этом объеме выделится тепло
где dV = dSdl - величина элементарного объема. Разделив выражение (5.24) на
dV и dt, найдем количество теплоты, выделяющееся в единице объема в единицу времени (удельную тепловую мощность тока)
Qуд = ρj 2 (5.25)
Выражение (5.25) представляет собой дифференциальную форму закона Джоуля-Ленца.
Расчет сложных (разветвленных) цепей постоянного тока заключается в отыскании по заданным сопротивлениям участков цепи и приложенным к ним ЭДС, сил токов в каждом участке. Для решения этой задачи применяются правила Кирхгофа.
Первое правило: Алгебраическая сумма токов, сходящихся в узле, равна нулю:
где n – число проводников, сходящихся в узле. Узлом в разветвленной цепи называется точка, в которой имеется более двух возможных направлений тока. Положительными считаются токи, подходящие к узлу, отрицательными – токи, отходящие от него.
Второе правило: В замкнутом контуре разветвленной цепи алгебраическая сумма падений напряжений равна алгебраической сумме ЭДС всех источников в этом контуре:
Читайте также:
