Основные положения классической теории электропроводности металлов
§ 14.1 Основные положения классической теории электропроводности металлов
Согласно теории Друде-Лоренца носителями тока в металлах являются свободные электроны, что объясняет высокую электропроводность металлов. Ионы в процессе протекания тока через металл участия не принимают. Если бы это было так, то протекание тока через металл сопровождалось переносом вещества. В действительности этого не наблюдается (опыт Рикке).
Основные положения классической электронной теории металлов следующие:
12. Между узлами кристаллической решётки движутся свободные электроны, называемые электронами проводимости.
3. При наличии внешнего электрического поля Е на хаотическое движение свободных электронов накладывается их упорядоченное (направленное) движение – так называемый дрейф электронов в определённом направлении.
4. Электроны проводимости при своём движении сталкиваются с ионами решётки, столкновения между электронами проводимости не учитывается.
5. Внешнее поле не влияет на концентрацию носителей тока и среднее время их свободного пробега.
§ 14.2 Закон Ома и Джоуля-Ленца в классической электронной теории
Согласно закону равномерного распределения энергии по степеням свободы, на один электрон приходится средняя кинетическая энергия теплового движения


( k - постоянная Больцмана, Т – температура (на каждую степень свободы приходится энергия, равная , электрон рассматривается как материальная точка; следовательно, свободный электрон обладает тремя степенями свободы)).
При тепловом движении электроны испытывают соударения.
Путь, проходимый электронами между двумя последовательными соударениями, называют длиной свободного пробега (рис.14.2).
Если по проводнику течёт постоянный ток, то внутри проводника существует электрическое поле, напряжённостью Е. На каждый электрон со стороны электрического поля действует сила F=eE, где е – заряд электрона. Под действием этой силы электрон приобретает ускорение а, которое можно определить из равенства mea =еЕ, откуда

(14.1)
( me - масса электрона).
Если t>– среднее время между двумя последовательными соударениями, то к концу свободного пробега электрон приобретает скорость

(14.2)
Средняя скорость упорядоченного движения электронов

(14.3)
(начальная скорость считается равной нулю, поэтому движение равноускоренное).
Среднее время между двумя последовательными соударениями можно определит, если знать длину свободного пробега и среднюю скорость теплового движения υτ>:

(14.4)
Вообще, , но соотношение (14.4) справедливо, так как уже было показано, что
Подставив из (3.99) в формулу (3.98), получим

(14.5)
Подставив в формулу j = neυ> (13.37) , получим

(14.6)

(14. 7)
- удельная проводимость материала проводника (величина, обратная его удельному сопротивлению)).
Единица удельной проводимости – сименс на метр (См/м)
Из выражения (3.101), представляющего закон Ома, следует: плотность тока пропорциональна напряжённости электрического поля, что совпадает с (3.81).
Из формулы (3.101) легко получить закон Ома в виде , для этого её правую и левую части надо умножить наS – площадь поперечного сечения проводника. Учитывая, что , получаем, но, а(поле внутри проводника длиной ℓ считаем однородным); следовательно,

(14.8)
Классическая электронная теория проводимости Друде-Лоренца
Теория Друде была разработана в 1900 году, через три года после открытия электрона. Затем теория была доработана Лоренцом, и сейчас она является классической и актуальной теорией проводимости металлов.
Электронная теория Друде-Лоренца
Согласно теории, носителями тока в металлах являются свободные электроны.
Друде предположил, что электроны в металле подчиняются и могут быть описаны уравнениями молекулярно-кинетической теории. Другими словами, свободные электроны в металле подчиняются законам МКТ и образуют "электронный газ".
Двигаясь в металле, электроны соударяются между собой и с кристаллической решеткой (это и есть проявление электрического сопротивления проводника). Между соударениями электроны, по аналогии с длиной свободного пробега молекул идеального газа, успевают преодолеть средний путь λ .
Без действия электрического поля, ускоряющего электроны, кристаллическая решетка и электронный газ стремятся к состоянию теплового равновесия.
Приведем основные положения теории Друде:
- Взаимодействие электрона с другими электронами и ионами не учитывается между столкновениями.
- Столкновения являются мгновенными событиями, внезапно меняющими скорость электрона.
- Вероятность для электрона испытать столкновение за единицу времени равна 1 τ .
- Состояние термодинамического равновесия достигается благодаря столкновениям.
Несмотря на множество допущений, теория Друде-Лорецна хорошо объясняет эффект Холла, явление удельной проводимости и теплопроводность металлов. Именно поэтому она актуальна по сей день, хотя ответы на многие вопросы (например, почему в металле существуют свободные ионы и электроны) смогла дать только квантовая теория твердого тела.
В рамках теории Друде объясняется сопротивление металлов. Оно обусловлено соударениями электронов с узлами кристаллической решетки.
Выделение тепла, согласно закону Джоуля-Ленца, также происходит по причине соударения электронов с ионами решетки.
Теплопередача в металлах также осуществляется электронами, а не кристаллической решеткой.
Терия Друде не объясняет многих явлений, как например сверхпроводимость, и не применима в сильных магнитных полях, в слабых магнитных полях может терять применимость из-за квантовых явлений.
Среднюю скорость электронов можно вычислить по формуле для идеального газа:
Здесь k - постоянная Больцмана, T - температура металла, m - масса электрона.
При включении внешнего электрического поля, на хаотичное движение частиц "электронного газа" накладывается упорядоченное движение электронов под действием сил поля, когда электроны начинают упорядоченно двигаться со средней скоростью u . Величину этой скорости можно оценить из соотношения:
где j - плотность тока, n - концентрация свободных электронов, q - заряд электрона.
При больших плотностях тока рассчеты дают следующий результат: средняя скорость хаотичного движения электронов во много раз ( ≈ 10 8 ) больше скорости упорядоченного движения под действием поля. При вычислении суммарной скорости полагают, что
Формула Друде
Формула Друде выводится из кинетического уравнения Больцмана и имеет вид:
Здесь m * - эффективная масса электрона, τ - время релаксации, то есть время, за которое электрон "забывает" о том, в какую сторону двигался после соударения.
Друде вывел закон Ома для токов в металле:
Опыт Толмена и Стюарта
В 1916 году опыт Толмена и Стюарта дал прямое доказательство тому, что носителями тока в металлах являются электроны.
Суть опыта была в следующем.
Опыт Толмена и Стюарта
Проводящая катушка с проводом длиной L вращалась вокруг своей оси с большой скоростью, а ее концы были замкнуты на гальванометр. Когда катушку резко тормозили, свободные электроны в металле продолжали двигаться по инерции, и гальванометр регистрировал импульс тока.
Считая, что свободные электроны подчиняются законам механики Ньютона, можно записать, что при остановке проводника электрон приобретает ускорение v ' (в катушке направлено вдоль проводов). При этом на электрон действует сила, направленная противоположно ускорению.
Под воздействием этой силы электрон ведет себя так, как если бы на него действовало поле E = - m v ' q . Эдс, возникающую в катушке при торможении можно записать, как:
ε = ∫ L E d l = - m v ' q ∫ L d l = - m v ' q L
Считая, что ускорение одинаково в каждом витке, можно записать закон Ома для катушки, а затем вычислить заряд, проходящий в ней за время d t :
d q = I d t = - m L d v q R d t d t = - m L d v q R
Заряд, прошедший от момента начала торможения до остановки:
q = - m L q R ∫ v 0 0 d v = - m L v 0 q R
Опыт Толмена и Стюарта получил хорошее согласование с теорией, полученное экспериментально отношение q m соответствовало отношению заряда электрона к его массе.
При T = 300 К вычислите среднюю скорость теплового движения свободных электронов.
3. Электрические токи в металлах, вакууме и полупроводниках
3.1. Опытные доказательства электронной проводимости металлов.
Электронная теория проводимости металлов была впервые создана в 1900 г. немецким физиком П.Друде и впоследствии разработана нидерландским физиком Х.Лоренцем. Основным ее положением является то, что носителями тока в металлах служат свободные электроны. Это подтверждалось рядом классических опытов.
В опыте К.Рикке (1901 г.) электрический ток в течение года пропускался через три последовательно соединенных металлических цилиндра (Cu, Al, Cu) с отшлифованными торцами одинакового радиуса. Общий заряд, прошедший через цилиндры, равнялся 3.510 6 Кл. Проведенное после этого взвешивание показало, что вес цилиндров не изменился, также не было обнаружено проникновения одного металла в другой. Следовательно, перенос заряда осуществлялся не ионами, а общими для всех металлов частицами - электронами.
Для подтверждения этого положения необходимо было определить знак и величину удельного заряда q/m (заряда единицы массы) носителей тока. Идея опытов и их качественное воплощение принадлежит российским физикам Л.Мандельштаму и Н.Папалески (1913 г.). Если движущийся поступательно проводник резко остановить, то, подключенный к нему гальванометр зафиксирует кратковременный ток. Это объясняется тем, что носители тока не связаны жестко с кристаллической решеткой и при торможении продолжают двигаться по инерции. По направлению тока гальванометра было определено, что знак заряда носителя тока - отрицательный. Согласно численному расчету, удельный заряд носителя тока оказался приблизительно равным удельному заряду электрона. К таким же результатам привели опыты Ч.Стюарта и Т.Толмена (1916 г.), в которых быстрые крутильные колебания катушки, соединенной с чувствительным гальванометром, создавали переменный электрический ток. Таким образом, было доказано, что носителями электрического тока в металлах являются свободные электроны.
Свободные электроны - это валентные электроны атомов металла, наиболее слабо связанные с ядрами атомов. Они легко отрываются, переходят от одного атома к другому и являются как бы “обобществленными”. Атомы, оставшиеся без нескольких электроонов ‑ положительные ионы, колеблются около некоторых точек равновесия, называемых узлами кристаллической решетки, и мешают свободному движению электронов.
3.2. Основные положения классической теории электропроводности металлов
С позиций классической электронной теории высокая электропроводность металлов обусловлена наличием огромного числа свободных электронов, движение которых подчиняется законам классической механики Ньютона. В этой теории пренебрегают взаимодействием электронов между собой, а взаимодействие их с положительными ионами сводят только к соударениям. Иными словами, электроны проводимости рассматриваются как электронный газ, подобный одноатомному, идеальному газу. Такой электронный газ должен подчиняться всем законам идеального газа. Следовательно, средняя кинетическая энергия теплового движения электрона будет равна , где- масса электрона,- его среднеквадратичная скорость,k - постоянная Больцмана, Т - термодинамическая температура. Отсюда при Т=300 К среднеквадратичная скорость теплового движения электронов 10 5 м/с.
Хаотичное тепловое движение электронов не может привести к возникновению электрического тока, но под действием внешнего электрического поля в проводнике возникает упорядоченное движение электронов со скоростью . Оценить величину можно изранее выведенного соотношения , гдеj - плотность тока, - концентрация электронов,e - заряд электрона. Как показывает расчет, 810 -4 м/с. Чрезвычайно малое значение величины объясняется весьма частыми столкновениями электронов с ионами решетки. Казалось бы, полученный результат для под действием поля возникнет практически сразу же на всем протяжении цепи, что и обеспечивает мгновенную передачу сигнала.
На базе классической электронной теории были выведены рассмотренные выше основные законы электрического тока - законы Ома и Джоуля-Ленца в дифференциальной форме . Кроме того, классическая теория дала качественное объяснение закону Видемана-Франца. В 1853 г. И.Видеман и Ф.Франц установили, что при определенной температуре отношение коэффициента теплопроводности к удельной проводимости одинаково для всех металлов. Закон Видемана-Франца имеет видВместе с тем классическая теория встретилась с существенными затруднениями. Перечислим некоторые из них :
1. Несоответствие теории и эксперимента возникло при расчете теплоемкости металлов. Согласно кинетической теории молярная теплоемкость металлов должна складываться из теплоемкости атомов и теплоемкости свободных электронов. Так как атомы в твердом теле совершают только колебательные движения, то их молярная теплоемкость равна С=3R (R=8.31 Дж/(мольК) - молярная газовая постоянная); свободные электроны двигаются только поступательно и их молярная теплоемкость равна С=3/2R. Общая теплоемкость должна быть С4.5R , но согласно опытным данным С=3R.
2. По расчетам электронной теории, сопротивление R должно быть пропорциональным3. Полученные опытным путем значения электропроводности дают для средней длины свободного пробега электронов в металлах величину порядка сотен междоузельных расстояний. Это гораздо больше, чем по классической теории .
Расхождение теории с опытом объясняется тем, что движение электронов в металле подчиняется не законам классической механики, а законам квантовой механики. Достоинством классической электронной теории являются простота, наглядность и правильность многих качественных ее результатов.
Основные сведения о электронной проводимости металлов в физике
Классическая (кинетическая) теория электропроводности металлов: понятие, обоснование
Электропроводность металлов — возможность тела (или же среды) проводить электрический ток; свойство объекта, среды, которое определяет формирование электрического тока в них под воздействием электрического поля.
Классическая теория электропроводности металлов была разработана и сформулирована в 1900 году немецким ученым-физиком Паулем Друде. Пауль Друде пользовался общими законами механики, законом Ома и другими.
Так выглядел Пауль Друде:
Эта теория была доработана другим ученым, Лоренцо. Сейчас данная теория является классической, а также актуальной в области проводимости металлов. Так теория электропроводности металлов называется теорией Друде-Лоренцо.
По данной теореме, носители тока в металлах могут быть только свободные электроны.
Друде считал, что электроны в металлах находятся в подчиненном состоянии, их можно описать посредством уравнения молекулярно-кинетической теории. Если говорить иными словами, свободные электроны в металлах подчинены законам МКТ (молекулярно-кинетической теории), они образуют «электронный газ».
Передвигаясь внутри металла, электроны ударяются между собой, а также кристаллической решеткой. Так проявляется электрическое сопротивление проводника. Между тем как электроны ударяются друг о друга, по аналогии с длиной свободного пробега молекул газа с идеальными характеристиками, они способны преодолеть усредненный путь, который принимается за λ .
Без воздействия электрического поля, которое ускоряет электроны, кристаллическая решетка, а также электронный газ стремятся к положению теплового равновесия.
Представим базовые положения теории Пауля Друде:
- Взаимодействие электрона с иными ионами и электронами не учитывают между столкновениями.
- Столкновения происходят мгновенно, они резко изменяют скорость электронов.
- Вероятность для электрона почувствовать столкновение в какую-то единицу времени будет равна соотношению 1 τ .
- Состояние термодинамического равновесия может достигаться с помощью столкновения.
Несмотря на то, что в теории достаточно много допущений, учение Друде-Лоренца может объяснить эффект Холла, теплопроводность металлов, а также феномен удельной проводимости. Из-за этого данная доктрина актуальна и в наши дни, хотя ответить на большую часть вопросов (к примеру, вопрос, почему в металле находятся свободные электроны и ионы) смогла лишь квантовая теория твердого тела.
В рамках учения Друде объясняется то, как происходит сопротивление металлов. Это явное преимущество теории. Сопротивление обуславливается взаимными ударениями электронов с узлами кристаллической решетки. Выделение тепла по закону Джоуля-Ленца тоже происходит из-за того, что электроны взаимно ударяются с ионами кристаллической решетки.
Передача тепла в металлах происходит с помощью электронов, а не при помощи кристаллической решетки.
Теория Друде не смогла объяснить такие явления, как, например, сверхпроводимость. Ее нельзя применить в сильных магнитных полях, в слабых магнитных полях данное учение может потерять свои свойства из-за квантовых явлений.
Среднюю скорость электронов возможно вычислить по формуле для газа с идеальными характеристиками: ( u p s i l o n ) = 8 k T π m , где
- k — постоянная Больцмана;
- t — температура металла;
- m — масса электрона.
Если включается внешнее электрическое поля, на движение частиц электронного газа хаотичного характера накладывается упорядоченное движение электронов под воздействием сил поля, когда электроны совершают упорядоченные движения со средней скоростью в ( u ) .
Величина скорости может быть оценена в рамках соотношения: j = n q ( u ) . В данном соотношении:
- j — плотность тока;
- n — концентрация свободных электронов;
- q — заряд электрона.
Если плотность тока большая, то расчеты будут давать такой итог: средняя скорость движения электронов хаотичного характера во много раз (примерно в 10 8 ) больше скорости упорядоченного движения под воздействием электрического поля.
В случае вычисления суммарной скорости считают, что ∣ ( v + u ) ∣ ≈ ∣ v ∣ .
Недостатки электронной теории проводимости
Лоренцем были произведены вычисления в виде: [ x σ = 3 ( k e ) 2 T . Данные расчеты считаются уточненными вычислениями с учетом классического распространения по скоростям. Они вызвали замену теоретической формулы множителя 3 на 2, что привело к быстрому увеличению расхождения опыта с теорией.
Второй недостаток классического электронного закона возникает в процессе сопоставления с опытом вычисления и формул для теплоемкостей.
Так по электронному закону теплоемкость единицы объема электронного газа будет равна C = 3 2 k n , где показатель n будет концентрацией электронов свободного типа. Теплоемкость, которая относится к одному электрону: C = 3 2 k n .
Давайте приведем пример одного килограмма атома одновалентного металла. В его составе есть N = 6 , 02 × 10 26 ионов, которые колеблются около собственных положений равновесия, а также N электронов свободного типа.
Колебательная теплоемкость твердого тела, согласно закону Дюлонга и Пти будет равна C = 3 R . Так теплоемкость электронного газа будет вычисляться по следующей формуле: C = 3 2 k N = 3 2 R .
Таким образом получается, что, согласно электронному закону теплоемкость одновалентных металлов должна составлять C = C 1 + C 2 = 9 2 R . Но по опыту получается так, что теплоемкость металлов, как и теплоемкость твердых диэлектриков, по закону Дюлонга и Пти, близится к 3 R . Так появилось непонятное и неожиданное явление практического отсутствия теплоемкости у электронного газа.
Третий недостаток классической электронной теории металлов считается невозможность хорошо объяснить при помощи данного закона зависимость температур сопротивления. Опыты показывают, что сопротивление металлических проводников постепенно растет вместе с температурой по закону R = R ( 1 + a T ) . То есть проводимость является обратно пропорциональной к абсолютной температуре в первой степени. Так σ = 1 T .
По классической теории проводимость является обратно пропорциональной T . В конце концов появились различные трудности в оценке средней длины свободного пробега электронов в металле.
Для того чтобы получились величины удельной электрической проводимости металла при использовании формулы, которые не имели бы отличий с опытными значениями, приходилось принимать среднюю длину свободного пробега электронов размером в сотни раз больше, чем период металлической решетки.
Другими словами, нужно предполагать, что электрон может проходить без взаимного ударения с ионами решетки сотни расстояний (межузельных). Данное предположение является странным в рамках классического электронного закона Друде-Лоренца.
Противоречия, которые приведены выше, указывают на тот факт, что классическая электронная теория, представляющая электрон как материальную точку, подчиняющуюся законам классической механики, не брала во внимание некоторые особенности электрона.
Они были еще не известны во времена, когда закон создавался. Данные свойства были найдены позднее, во время того, как изучалось строение атома. В 1924 году создали новейшую теорию, которую назвали волновой\квантовой механикой движения электронов.
Как отличается электропроводность разных металлов
Электронная теория электропроводности металлов начала развиваться из-за исследований ученого Пауля Друде. Он смог открыть сопротивление как свойство. Сопротивление наблюдается тогда, когда электрический ток проходит через проводник.
В будущем эта теория помогла типизировать различные вещества по их уровню проводимости. Из результатов исследования можно с легкостью понять, какой металл подходит для того, чтобы изготовить тот или иной кабель. Это самый важный момент, потому что материал, который неправильно подобран, может быть причиной перегрева, возгорания и других последствий.
Самая большая электропроводность у серебра. Она составляет 63,3 на 104 см при температуре +20 °C. Однако изготовление проводки из серебра — недешевое занятие, потому что серебро является достаточно редким и к тому же драгоценным металлом.
Металл, обладающий большой электропроводностью среди всех элементов из неблагородной группы — медь. Показатель у нее будет 57 на 104 см при температуре +20 °C. Медь — один из самых распространенных проводников, которые используются в производственных и бытовых целях. Она выдерживает частые электрические нагрузки, отличается надежностью и долговечностью. Высокая температура плавления помогает без проблем работать в нагретом состоянии достаточно долгое время.
Наравне с медью также распространен алюминий. Он находится на четвертом месте по электропроводности после золота. Алюминий используют в сетях с небольшим напряжением, потому что обладает вдвое меньшей температурой плавления, чем медь. Алюминий не может выдерживать большие нагрузки.
Электропроводность металлов можно узнать в таблице электропроводности.
Нужно отметить, что каждый сплав обладает меньшим уровнем проводимости, чем чистое вещество. Это может быть связано с тем, что структурная сетка сливается со всем остальным, происходит нарушение обычного электронного функционирования.
В производстве медного провода используют материал, который содержит менее 0,1 % примесей. Некоторые типы кабелей обладают показателем в не более, чем 0,05 %.
Материалы высокой проводимости
Электропроводность у щелочных металлов расположена на крайне высоком уровне, потому что у них электроны практические не привязаны к ядру, их можно легко выстроить в необходимую последовательность. Однако данная группа отличается тем, у них небольшая температура плавления, но большая химическая активность. В большинстве своем данные свойства не дают использовать эти металлы для того, чтобы изготовить провода.
Металлы с высоким уровнем электропроводности в открытом виде крайне опасны для людей. Прикосновение к оголенным проводам приведет к тому, что человек получит электрический ожог, а также электрический разряд будет взаимодействовать на внутренние органы. Часто это ведет к мгновенной смерти. Из-за этого для безопасности человека используют особенные изоляционные материалы.
В зависимости от области применения металлов изоляционные материалы могут быть жидкими, твердыми, газообразными. Однако главная их функция все же одна — изолировать электрический ток в цепи так, чтобы он не смог оказать никакого воздействия на окружающую среду.
Электропроводность металлов используют почти во всех областях в современной человеческой жизни, поэтому безопасность человека считается самой главной задачей.
Глава 14. Электрический ток в металлах, жидкостях и газах
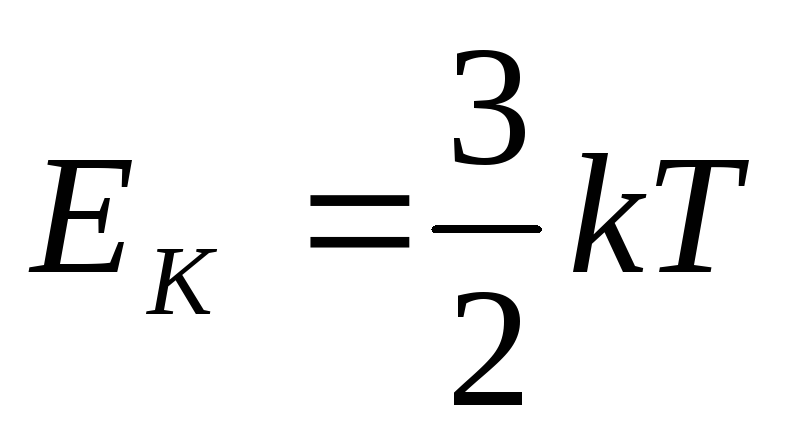

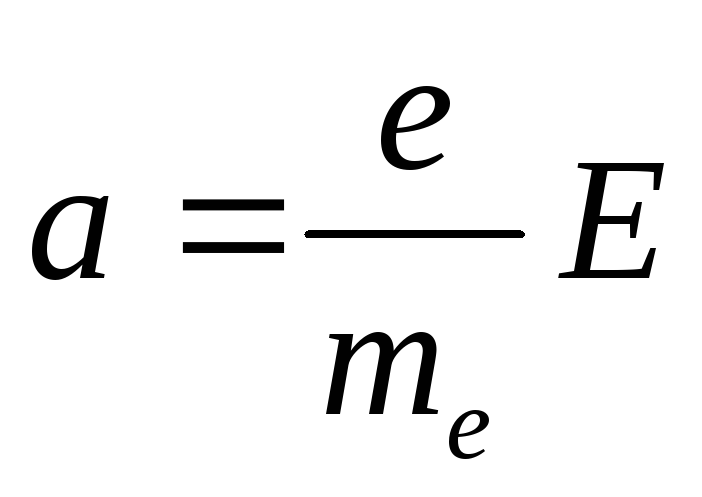

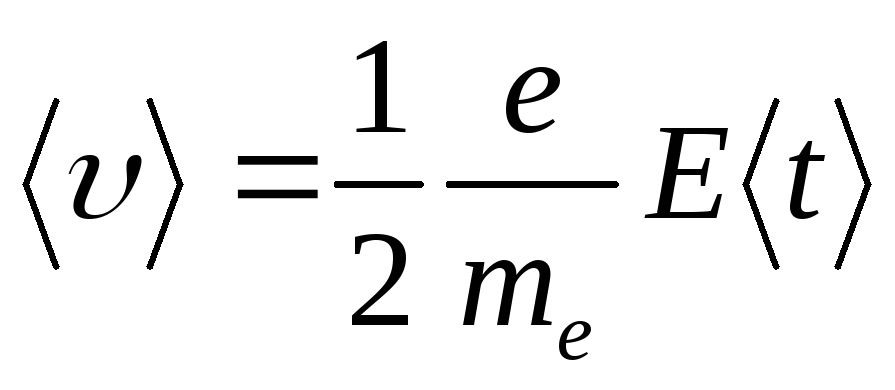
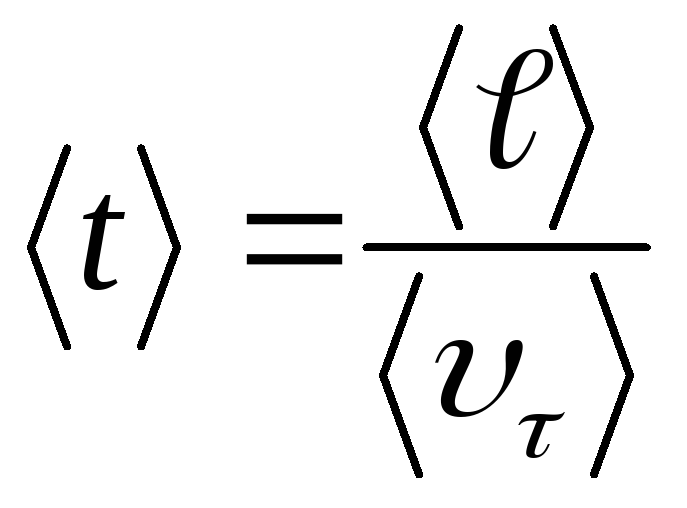
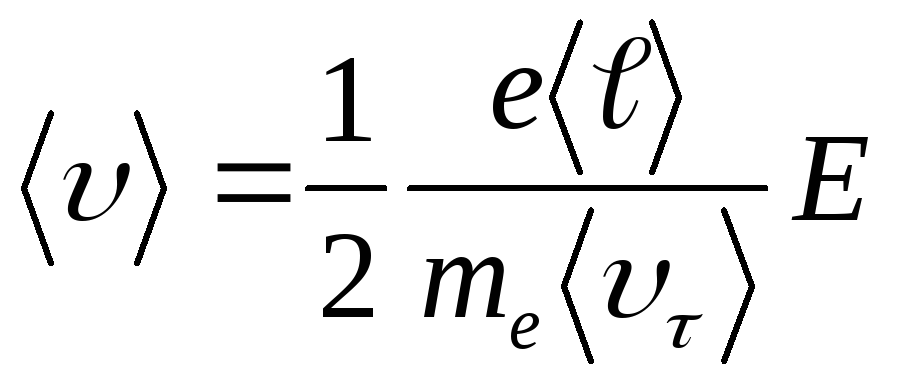
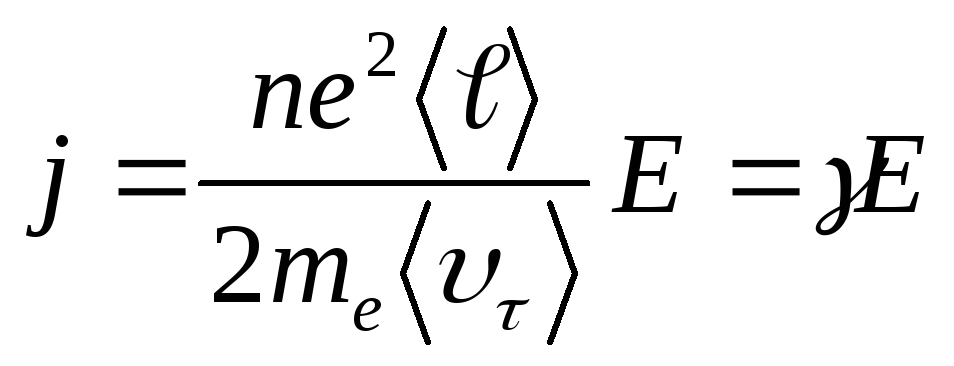


Читайте также:
