Объяснение природы электрического тока в металлах на основе представления о строении металлов
§ 34. Электрический ток в металлах. Сверхпроводимость
Типичными представителями класса проводников являются металлы. Какова природа электрического тока в металлах?
Природа электрического тока в металлах. В металлических проводниках носители электрического заряда — свободные электроны. Под действием внешнего электрического поля свободные электроны упорядоченно движутся, создавая электрический ток ( рис. 194 ).
Электронная проводимость металлов была впервые экспериментально подтверждена немецким физиком К. Рикке ( 1845–1915 ) в 1901 г. Суть опыта Рикке заключалась в следующем: по проводнику, состоявшему из трёх отполированных и плотно прижатых друг к другу цилиндров — двух медных и одного алюминиевого ( рис. 195 ), в течение года проходил ток одного и того же направления. За этот промежуток времени через проводник прошёл заряд более 3,5 МКл. После завершения опыта взвешивание показало, что массы цилиндров остались неизменными. Это явилось экспериментальным доказательством того, что перенос заряда при прохождении тока в металлах не сопровождается химическими процессами и переносом вещества, а осуществляется частицами, которые являются одинаковыми для всех металлов, т. е. электронами.
В 1916 г. американский физик Р. Толмен ( 1881—1948 ) и шотландский физик Т. Стюарт усовершенствовали методику этих опытов и выполнили количественные измерения, неопровержимо доказавшие, что ток в металлических проводниках обусловлен движением свободных электронов.
В этих опытах катушку с большим числом витков тонкой проволоки подключали к гальванометру и приводили в быстрое вращение вокруг своей оси ( рис. 195.1 ). При резком торможении катушки в цепи возникал кратковременный ток, обусловленный инерцией носителей заряда. По направлению отклонения стрелки гальванометра было установлено, что электрический ток создают отрицательно заряженные частицы. При этом экспериментально полученное отношение заряда каждой из этих частиц к её массе (удельный заряд) близко к удельному заряду электрона, полученному из других опытов. Так было экспериментально доказано, что носителями свободных зарядов в металлах являются электроны.
Вещества, обладающие электронной проводимостью, называют проводниками первого рода.
В соответствии с классической электронной теорией проводимости металлов, созданной немецким физиком П. Друде ( 1863–1906 ) в 1900 г., металлический проводник можно рассматривать как физическую систему, состоящую из свободных электронов и положительно заряженных ионов, колеблющихся около положений равновесия ( рис. 196 ).
Появление свободных электронов при образовании металлического кристалла из нейтральных атомов можно упрощённо объяснить следующим образом. Электроны, находящиеся на внешних оболочках атомов, слабо связаны со своими ядрами. При образовании кристалла атомы сближаются на расстояние r 0,1 нм , и электроны начинают взаимодействовать не только со своими ядрами, но и с ядрами соседних атомов. В результате этого их взаимодействие с собственными ядрами значительно ослабевает, вследствие чего они теряют с ними связь и могут двигаться по всему кристаллу в любом направлении как свободные частицы. Атомы превращаются при этом в положительно заряженные ионы. В пространстве между ионами беспорядочно движутся подобно частицам идеального газа свободные электроны. Поэтому для описания движения электронов используют модель «электронный газ» — совокупность свободных электронов в кристаллической решётке металла. На рисунке 196.1 пунктирной линией изображена траектория движения одного из электронов.
В этой модели электроны, упорядоченное движение которых является током проводимости, рассматривают как материальные точки, модуль потенциальной энергии взаимодействия которых пренебрежимо мал по сравнению с их кинетической энергией. Считают, что движение электронов под действием электрического поля подчиняется законам классической механики, а их столкновения с ионами кристаллической решётки металла являются неупругими, т. е. при столкновениях электроны полностью передают ионам кинетическую энергию своего упорядоченного движения. В промежутках между столкновениями свободные электроны совершают беспорядочное тепловое движение и в то же время движутся упорядоченно и равноускоренно под воздействием электрического поля.
Интересно знать
Модель электронного газа позволяет теоретически объяснить природу сопротивления и обосновать закон Ома для участка цепи, не содержащего источника тока, на основе классической электронной теории проводимости металлов. Проанализируем упорядоченное движение электронов проводимости.
Пусть электрон движется с ускорением в направлении, противоположном направлению напряжённости электрического поля ( рис. 196.2 ): где m0 — масса электрона, e — элементарный электрический заряд (модуль заряда электрона).
Тогда модуль средней скорости его направленного движения: , где — усреднённый промежуток времени между двумя последовательными столкновениями электрона с ионами кристаллической решётки.
Поскольку электрическое поле внутри однородного прямолинейного проводника с током однородное, то модуль напряжённости этого поля где l — длина проводника, U — напряжение между его концами. Тогда модуль средней скорости направленного движения электронов пропорционален напряжению между концами проводника .
Сила тока в проводнике пропорциональна модулю средней скорости направленного движения электронов:
где q — модуль заряда электронов проводимости, находящихся в проводнике, — усреднённое время прохождения этих электронов по проводнику, N — количество электронов проводимости в проводнике, n — концентрация этих электронов, V = Sl — объём проводника. Следовательно, сила тока пропорциональна напряжению между концами проводника I U.
Природа электрического тока в металлах. Сверхпроводимость
Металлы – хорошие проводники электрического тока. Проводимость в металлах обусловлена наличием в них свободных электронов, которые сравнительно легко отрываются от атомов. Образуя положительный ион и свободный электрон.
В отсутствие электрического поля электроны движутся беспорядочно, участвуя в тепловом (хаотическом) движении.
Под действием электрического поля электроны начинают упорядоченно перемещаться между ионами, находящимися в узлах кристаллической решетки, со средней скоростью порядка 10 -4 м/с, образуя электрический ток.
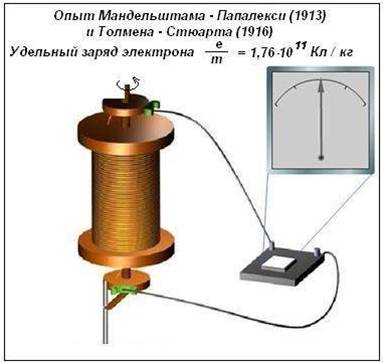
Экспериментальное доказательство того, что проводимость металлов обусловлена движением свободных электронов , было дано в опытах Л.И. Мандельштама и Н.Д. Папалекси в 1912г (результаты не были опубликованы), а также Т. Стюарта и Р. Толмена в 1916 г.
Идея опытов : если резко тормозить движущийся кусок металла, то находящиеся в нем свободные заряды, двигаясь по инерции, будут скапливаться у переднего его конца, и между концами проводника возникает разность потенциалов.
Опыт Мандельштама и Папалекси
Катушка, соединенная с телефоном, приводилась в колебательное движение вокруг своей оси. Благодаря инерции свободный зарядов на концах катушки возникала переменная разность потенциалов, и телефон издавал звук.
Это были лишь качественные опыты. Никакие измерения и количественные расчеты в этих опытах не были произведены.
Опыт Стюарта и Толмена
Катушка большого диаметра с намотанным на ней металлическим проводом приводилась в быстрое вращение и затем резко тормозилась. При торможении катушки свободные заряды в проводнике продолжали некоторое время двигаться по инерции. Вследствие движения зарядов относительно проводника в катушке возникал кратковременный электрический ток, который регистрировался гальванометром присоединённым к концам проводника с помощью скользящих контактов.
Направление тока свидетельствовало о том, что он обусловлен движением отрицательно заряженных частиц.
Измеряя заряд, проходящий через гальванометр за все время существования тока в цепи, удалось определить отношение q0/m. Оно оказалось равным 1,8*1011Кл/кг. Это значение совпадает со значением аналогичного отношения для электрона, найденным из других опытов.
Таким образом было экспериментально установлено, что носителями электрического тока в металлах являются свободные электроны.
Зависимость сопротивления проводника R от температуры:
Удельное сопротивление проводника зависит от температуры:
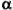
где ро - удельное сопротивление при 0 градусов, t - температура, - температурный коэффициент сопротивления ( т.е. относительное изменение удельного сопротивления проводника при нагревании его на один градус)
Для металлов и сплавов
Обычно для чистых металлов принимается
Таким образом, для металлических проводников с ростом температуры
увеличивается удельное сопротивление, увеличивается сопротивление проводника и уменьшается эл.ток в цепи.
Низкотемпературная сверхпроводимость:
наблюдается при сверхнизких температурах (ниже 25 К) во многих металлах и сплавах; при таких температурах удельное сопротивление этих веществ становится ничтожно малым.
В 1986 г. открыта (для металлокерамики) высокотемпературная сверхпроводимость (при 100 К).
Трудность достижения сверхпроводимости:
- необходимость сильного охлаждения вещества
Область применения:
- получение сильных магнитных полей;
- мощные электромагниты со сверхпроводящей обмоткой в ускорителях и генераторах.
Физика 8 класс! Какие будут задания на этот экзамен? Или как отвечать на эти вопросы?
Билет № 1.
1. Тепловое движение молекул и температура. Внутренняя энергия тела и способы её изменения. Объяснение внутренней энергии на основе учения о молекулярном строении вещества.
2. Лабораторная работа: «Измерение мощности и работы тока в электрической лампе»
Билет № 2.
1. Виды теплопередачи. Примеры теплопередачи в природе быту технике. Опыты, иллюстрирующие виды теплопередачи.
2. Задача на параллельное соединение проводников.
Билет № 3.
1. Количество теплоты. Удельная теплоёмкость вещества, физический смысл и единицы измерения. Формула для определения количества теплоты, выделяемого или поглощаемого при изменении температуры тела.
2. Задача на построение изображения в собирающей линзе.
Билет № 4.
1. Плавление и отвердевание кристаллических тел. Удельная теплота плавления и кристаллизации, физический смысл и единицы измерения. Объяснение процессов плавления и отвердевания на основе учения о молекулярном строении вещества. Формула для определения количества теплоты, выделяемого или поглощаемого при плавлении или отвердевании.
2. Задача на последовательное соединение проводников.
Билет № 5.
1. Испарение и конденсация. Удельная теплота испарения и конденсации, физический смысл и единицы измерения. Объяснение процессов испарения и конденсации на основе учения о молекулярном строении вещества. Формула для определения количества теплоты, выделяемого или поглощаемого при испарении и конденсации.
2. Лабораторная работа: «Регулирование силы тока реостатом».
Билет № 6.
1. Двигатель внутреннего сгорания. Объяснение принципа действия, устройства и применения.
2. Задача на построение изображения предмета в рассеивающей линзе.
Билет № 7.
1. Электризация тел. Опыты, иллюстрирующие явление электризации тел. Два рода электрических зарядов. Взаимодействие заряженных тел. Объяснение явления электризации на основе учения о строении атома.
2. Задача на применение закона отражения света.
Билет № 8.
1. Делимость электрического заряда. Опыт, иллюстрирующий делимость заряда. Ядерная модель атома.
2. Задача на построение изображения в плоском зеркале.
Билет № 9.
1. Электрический ток и его действия. Объяснение природы электрического тока в металлах на основе представления о строении металлов.
2. Задача на расчёт количества теплоты, необходимого для нагревания тела.
Билет № 10.
1. Сила тока. Единицы силы тока. Амперметр и его включение в цепь.
2. Задача на расчёт количества теплоты, необходимого для плавления тела.
Билет № 11.
1. Электрическое напряжение. Единицы напряжения. Вольтметр и его включение в цепь.
2. Задача на расчёт количества теплоты, необходимого для парообразования.
Билет № 12.
1. Электрическое сопротивление проводников и единицы измерения. Расчёт сопротивления проводника. Удельное сопротивление, единицы измерения и его физический смысл.
2. Задача на расчёт количества теплоты, выделяемого при сгорании топлива.
Билет № 13.
1. Закон Ома для участка цепи. Опытное подтверждение закона Ома.
2. Задача на расчёт КПД теплового двигателя.
Билет № 14.
1. Работа и мощность электрического тока. Формулы для вычисления работы и мощности. Единицы измерения и их физический смысл.
2. Задача на расчёт удельной теплоёмкости твёрдого тела.
Билет № 15.
1. Нагревание проводников электрическим током. Объяснение этого явления. Закон Джоуля-Ленца и его применение.
2. Лабораторная работа: «Определение фокусного расстояния собирающей линзы».
Билет № 16.
1. Магнитное поле. Опытное подтверждение связи электрического тока и магнитного поля. Магнитные линии. Электромагниты и их применение.
2. Лабораторная работа: «Сборка электрической цепи и измерение силы тока в различных её участках».
Билет № 17.
1. Постоянные магниты. Магнитное поле Земли.
2. Задача на расчёт сопротивления проводника.
Внутренняя энергия — это энергия движения и взаимодействия частиц, из которых состоит тело.
Внутренняя энергия зависит от температуры тела, его агрегатного состояния, от химических, атомных и ядерных реакций. Она не зависит ни от механического движения тела, ни от положения этого тела относительно других тел.
«холодный», «тёплый» и «горячий», мы указываем на различную степень нагретости тел, или, как говорят в физике, на различную температуру тел. Температура горячей воды выше температуры холодной. Температура воздуха летом выше, чем зимой.
Температуру тел измеряют с помощью термометра и выражают в градусах Цельсия (°С).
Вам уже известно, что диффузия при более высокой температуре происходит быстрее. Это означает, что скорость движения молекул и температура связаны между собой. При повышении температуры скорость движения молекул увеличивается, при понижении — уменьшается.
Следовательно, температура тела зависит от скорости движения молекул.
все вещества состоят из отдельных частиц - молекул, которые беспорядочно (в той или иной степени) движутся и взаимодействую друг с другом. При подсчёте кинетической и потенциальной энергии используются характеристики тела как единого целого, так что энергия, связанная с молекулами, не учитывается. Однако на то, чтобы "заморозить" все входящие в состав тела частицы, т. е. почти остановить все молекулы, а также "растащить" все частицы вещества на далёкое расстояние, нужно затратить некоторую (вообще говоря, довольно большую) энергию. Как раз эту энергию и называют внутренней, т. к. она связана не с макроскопической структурой вещества, а с микроскопической, связанной с молекулами или атомами, входящими в его состав.
дальше сам делай
Билет №1 Вопрос 1
Примерно так: все вещества состоят из отдельных частиц - молекул, которые беспорядочно (в той или иной степени) движутся и взаимодействую друг с другом. При подсчёте кинетической и потенциальной энергии используются характеристики тела как единого целого, так что энергия, связанная с молекулами, не учитывается. Однако на то, чтобы "заморозить" все входящие в состав тела частицы, т. е. почти остановить все молекулы, а также "растащить" все частицы вещества на далёкое расстояние, нужно затратить некоторую (вообще говоря, довольно большую) энергию. Как раз эту энергию и называют внутренней, т. к. она связана не с макроскопической структурой вещества, а с микроскопической, связанной с молекулами или атомами, входящими в его состав.
SA. Ток в металлах
В начале XX века была создана классическая электронная теория проводимости металлов (П. Друде, 1900 г., Х.Лоренц, 1904 г.), которая дала простое и наглядное объяснение большинства электрических и тепловых свойств металлов.
Рассмотрим некоторые положения этой теории.
Свободные электроны
Металлический проводник состоит из:
1) положительно заряженных ионов, колеблющихся около положения равновесия, и
2) свободных электронов, способных перемещаться по всему объему проводника.
Таким образом, электрические свойства металлов обусловлены наличием в них свободных электронов с концентрацией порядка 10 28 м –3 , что примерно соответствует концентрации атомов. Эти электроны называются электронами проводимости. Они образуются путем отрыва от атомов металлов их валентных электронов. Такие электроны не принадлежат какому-то определенному атому и способны перемещаться по всему объему тела.
В металле в отсутствие электрического поля электроны проводимости хаотически движутся и сталкиваются, чаще всего с ионами кристаллической решетки (рис. 1). Совокупность этих электронов можно приближенно рассматривать как некий электронный газ, подчиняющийся законам идеального газа. Средняя скорость теплового движения электронов при комнатной температуре составляет примерно 10 5 м/с.
Электрический ток в металлах
Ионы кристаллической решетки металла не принимают участие в создании тока. Их перемещение при прохождении тока означало бы перенос вещества вдоль проводника, что не наблюдается. Например, в опытах Э. Рикке (1901 г.) масса и химический состав проводника не изменялся при прохождении тока в течении года.
Экспериментальное доказательство того, что ток в металлах создается свободными электронами, было дано в опытах Л.И. Мандельштама и Н. Д. Папалекси (1912 г., результаты не были опубликованы), а также Т. Стюарта и Р. Толмена (1916 г.). Они обнаружили, что при резкой остановке быстро вращающейся катушки в проводнике катушки возникает электрический ток, создаваемый отрицательно заряженными частицами — электронами.
- электрический ток в металлах — это направленное движением свободных электронов.
Так как электрический ток в металлах образуют свободные электроны, то проводимость металлических проводников называется электронной проводимостью.
Электрический ток в металлах возникает под действием внешнего электрического поля. На электроны проводимости, находящиеся в этом поле, действует электрическая сила, сообщающая им ускорение, направленное в сторону, противоположную вектору напряженности поля. В результате электроны приобретают некоторую добавочную скорость (ее называют дрейфовой). Эта скорость возрастает до тех пор, пока электрон не столкнется с атомом кристаллической решетки металла. При таких столкновениях электроны теряют свою избыточную кинетическую энергию, передавая ее ионам. Затем электроны снова разгоняются электрическим полем, снова тормозятся ионами и т.д. Средняя скорость дрейфа электронов очень мала, около 10 –4 м/с.
- Скорость распространения тока и скорость дрейфа не одно и то же. Скорость распространения тока равна скорости распространения электрического поля в пространстве, т.е. 3⋅10 8 м/с.
- При столкновении с ионами электроны проводимости передают часть кинетической энергии ионам, что приводит к увеличению энергии движения ионов кристаллической решетки, а, следовательно, и к нагреванию проводника.
Сопротивление металлов
Сопротивление металлов объясняется столкновениями электронов проводимости с ионами кристаллической решетки. При этом, очевидно, чем чаще происходят такие столкновения, т. е. чем меньше среднее время свободного пробега электрона между столкновениями τ, тем больше удельное сопротивление металла.
В свою очередь, время τ зависит от расстояния между ионами решетки, амплитуды их колебаний, характера взаимодействия электронов с ионами и скорости теплового движения электронов. С ростом температуры металла амплитуда колебаний ионов и скорость теплового движения электронов увеличиваются. Возрастает и число дефектов кристаллической решетки. Все это приводит к тому, что при увеличении температуры металла столкновения электронов с ионами будут происходить чаще, т.е. время τ уменьшается, а удельное сопротивление металла увеличивается.
См. так же
Зависимость сопротивления от температуры
Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления от температуры выражается линейной функцией:
\(~\rho = \rho_0 \cdot (1 + \alpha \cdot \Delta t),\)
где Δt = t - t0, t0 = 0 °C, ρ0, ρ — удельные сопротивления вещества проводника соответственно при 0 °С и t °C, α — температурный коэффициент сопротивления, измеряемый в СИ в Кельвинах в минус первой степени (К -1 ) (или °C -1 ).
- Температурный коэффициент сопротивления вещества — это величина, численно равная относительному изменению удельного сопротивления проводника при его нагревании на 1 К:
Для всех металлических проводников α > 0 и слабо изменяется с изменением температуры. Для большинства металлов в интервале температур от 0 ° до 100 °С коэффициент α изменяется от 3,3⋅10 –3 до 6,2⋅10 –3 К –1 (таблица 1). У химически чистых металлов α = 1/273 К -1 .
- Существуют специальные сплавы, сопротивление которых практически не изменяется при нагревании, например, манганин и константан. Их температурные коэффициенты сопротивления очень малы и равны соответственно 1⋅10 –5 К –1 и 5⋅10 –5 К –1 .
Температурный коэффициент сопротивления (при t от 0 °С до 100 °C)
| Вещество | α, 10 –3 °К –1 | Вещество | α, 10 –3 °К –1 |
|---|---|---|---|
| Алюминий | 4,2 | Нихром | 0,1 |
| Вольфрам | 4,8 | Олово | 4,4 |
| Железо | 6,0 | Платина | 3,9 |
| Золото | 4,0 | Ртуть | 1,0 |
| Латунь | 0,1 | Свинец | 3,7 |
| Магний | 3,9 | Серебро | 4,1 |
| Медь | 4,3 | Сталь | 4,0 |
| Никель | 6,5 | Цинк | 4,2 |
Если пренебречь изменением размеров металлического проводника при нагревании, то такую же линейную зависимость от температуры будет иметь и его сопротивление
\(~R_t = R_0 \cdot (1 + \alpha \cdot \Delta t) ,\)
где R0, Rt — сопротивления проводника при 0 °С и t °С.
Зависимость удельного сопротивления металлических проводников ρ от температуры t изображена на рисунке 2.

Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве термометрического тела такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры достаточно изучена. Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Сверхпроводимость
В 1911 г. голландский физик Г. Камерлинг-Оннес, изучая изменение электрического сопротивления ртути при низких температурах, обнаружил, что при температуре около 4 К (т.е. при –269 °С) удельное сопротивление скачком уменьшается (рис. 3) до нуля. Это явление Г. Камерлинг-Оннес назвал сверхпроводимостью.

Г. Камерлинг-Оннес был удостоен Нобелевской премии по физике 1913 г. «за исследования свойств вещества при низких температурах».
В дальнейшем было выяснено, что более 25 химических элементов — металлов при очень низких температурах становятся сверхпроводниками. У каждого из них своя критическая температура перехода в состояние с нулевым сопротивлением. Самое низкое значение ее у вольфрама — 0,012 К, самое высокое у ниобия — 9 К.
Сверхпроводимость наблюдается не только у чистых металлов, но и у многих химических соединений и сплавов. При этом сами элементы, входящие в состав сверхпроводящего соединения, могут и не являться сверхпроводниками. Например, NiBi, Au2Bi, PdTe, PtSb и другие.
До 1986 г. были известны сверхпроводники, обладающие этим свойством при очень низких температурах — ниже –259 °С. В 1986-1987 годах были обнаружены материалы с температурой перехода в сверхпроводящее состояние около –173 °С. Это явление получило название высокотемпературной сверхпроводимости, и для его наблюдения можно использовать вместо жидкого гелия жидкий азот.
Широкому применению сверхпроводимости до недавнего времени препятствовали трудности, связанные с необходимостью охлаждения до сверхнизких температур, для чего использовался жидкий гелий. Тем не менее, несмотря на сложность оборудования, дефицитность и дороговизну гелия, с 60-х годов XX века создаются сверхпроводящие магниты без тепловых потерь в их обмотках, что сделало практически возможным получение сильных магнитных полей в сравнительно больших объемах. Именно такие магниты требуются для создания установок управляемого термоядерного синтеза с магнитным удержанием плазмы, для мощных ускорителей заряженных частиц. Сверхпроводники используются в различных измерительных приборах, прежде всего в приборах для измерения очень слабых магнитных полей с высочайшей точностью.
На основе сверхпроводящих пленок создан ряд быстродействующих логических и запоминающих элементов для счетно-решающих устройств. При космических исследованиях перспективно использование сверхпроводящих соленоидов для радиационной защиты космонавтов, стыковки кораблей, их торможения и ориентации, для плазменных ракетных двигателей.
В настоящее время созданы керамические материалы, обладающие сверхпроводимостью при более высокой температуре — свыше 100 К, то есть при температуре выше температуры кипения азота. Возможность охлаждать сверхпроводники жидким азотом, который имеет на порядок более высокую теплоту парообразования, существенно упрощает и удешевляет все криогенное оборудование, обещает огромный экономический эффект.
- Wikipedia Сверхпроводимость
- Буздин А., Варламов А. Страсти по сверхпроводимости в конце тысячелетия //Квант. — 2000. — № 1. — С. 2-8.
- Мякишев Г.Я. Физика: Электродинамика //§2.6. Сверхпроводимость
Недостатки электронной теории проводимости
Несмотря на то, что электронной теории проводимости металлов объяснила ряд явлений, она имеет и свои недостатки.
- Из теории следовало, что удельное сопротивление должно быть пропорционально корню квадратному из температуры (\(~\rho \sim \sqrt T\)), между тем, согласно опыту, ρ ~ Т.
- Для того чтобы получить значения удельной электрической проводимости металла, полученных из опыта, приходится принимать среднюю длину свободного пробега электронов в сотни раз большей, чем период решетки металла. Иными словами, электрон должен проходит без соударений с ионами решетки сотни атомов.
- Данная теория не смогла объяснить причину сверхпроводимости.
Приведенные выше недостатки указывают на то, что классическая электронная теория, представляя электрон как материальную точку, подчиняющуюся законам классической механики, не учитывала некоторых специфических свойств самого электрона, которые еще не были известны к началу XX века. Эти свойства были установлены позднее при изучении строения атома, и в 1924 г. была создана новая, так называемая квантовая или волновая механика движения электронов.
Читайте также:
