Найти взаимную емкость системы из двух одинаковых металлических шариков
Электрическая емкость — последняя тема главы «Электростатика». При решении задач на эту тему могут потребоваться все сведения, полученные при изучении электростатики: сохранение электрического заряда, понятия напряженности поля и потенциала, поведение проводников в электростатическом поле, изменение напряженности поля в диэлектриках, закон сохранения энергии применительно к электростатическим явлениям. Только при хорошем усвоении всех основных понятий электростатики решение задач на электрическую емкость не вызовет особых затруднений.
Основными формулами при решении задач на емкость являются следующие: формула (1.24.2) — определение емкости, формула (1.24.3) — емкость уединенного шара, выражения для емкости плоского конденсатора (1.25.3) и сферического конденсатора (1.25.7), а также формулы для определения емкости батареи конденсаторов при последовательном и параллельном их соединении (1.26.4) и (1.26.2).
Надо знать еще формулы (1.27.3) и (1.27.9) для энергии заряженного конденсатора и заряженного уединенного тела.
Задача 1
Два одинаковых металлических шарика радиусом г расположены в вакууме на расстоянии d друг от друга, причем d >> r. Шарики заряжены одинаковыми по модулю и противоположными по знаку зарядами. Какова электрическая емкость системы, образованной шариками?
Решение. Искомая емкость равна отношению заряда q одного из шариков к разности потенциалов между ними:
Найдем U. Потенциал φ1 первого шарика, несущего заряд +q, складывается из его собственного потенциала : (см. задачу 16 § 1.23).

Аналогично потенциал второго шарика

Отсюда разность потенциалов

Поскольку d >> r, то с большой степенью точности можно считать, что
Задача 2
Найдите емкость С конденсатора, площадь пластин которого S и расстояние между ними l, если в конденсатор вставлена металлическая пластина толщиной d, параллельная его обкладкам (рис. 1.107).

Решение. Конденсатор со вставленной в него пластиной можно рассматривать как два последовательно соединенных конденсатора. Емкость первого из них . При последовательном соединении электрическая емкость батареи определяется уравнением:

Емкость не зависит от положения пластины. При очень тонкой пластине (d ⇒ 0) емкость конденсатора не зависит от наличия пластины.
Задача 3
В плоский конденсатор с расстоянием d между обкладками вводится диэлектрическая пластина, толщина которой d1 < d.
Определите емкость конденсатора с диэлектрической пластиной. Диэлектрическая проницаемость материала пластины ε. Площадь пластины и каждой обкладки конденсатора S.
Решение. Если в плоский конденсатор внести очень тонкую проводящую пластину, параллельную обкладкам, то на ее поверхностях появятся заряды противоположных знаков, равные по модулю. При этом емкость конденсатора не изменяется (см. задачу 2). Поэтому можно считать, что на поверхностях диэлектрической пластины нанесены тонкие проводящие слои. В этом случае образуются три последовательно соединенных конденсатора с емкостями

где d2 и d3 — расстояния между поверхностями диэлектрической пластины и обкладками, причем d2 + d2 = d - d1 (рис. 1.108).

Емкость С батареи из трех конденсаторов определяется из формулы


Задача 4
Ha рисунке 1.109 изображена батарея конденсаторов. Их емкости равны С1 = C, C2 = 2С, C3 = ЗС, С4 = 6С. Изменится ли емкость батареи, если между точками А и В включить конденсатор с емкостью C5 = 8С?

Решение. Обозначим потенциалы на зажимах батареи φ1 и φ2, а в точках А и В соответственно φ3 и φ4.
Так как конденсаторы С1 и СЗ соединены последовательно, то их заряды одинаковы, т.е.


Разделив почленно равенство (1.28.1) на равенство (1.28.2) и учитывая, что, согласно условию задачи,

Отсюда найдем, что φ3 = φ4. т. е. точки А и В имеют одинаковые потенциалы. Поэтому если включить какой-либо конденсатор между точками А и В (рис. 1.110), то он не зарядится и, следовательно, не повлияет на емкость системы.


Схема, подобная схеме, изображенной на рисунке 1.110, называется мостовой. Конденсаторы С1 и С2, СЗ и С4 называются плечами моста. Обратите внимание, что если емкости плеч моста пропорциональны , то точки А и В имеют одинаковые потенциалы. Конденсатор С5 не заряжается, и его из схемы можно удалить (см. рис. 1.109).
Задача 5
Найдите емкость батареи конденсаторов, изображенной на рисунке 1.111. Емкость каждого конденсатора равна С.

Решение. Данная схема соединения конденсаторов эквивалентна схеме, изображенной на рисунке 1.112. В этом можно убедиться, проверив, что каждый из конденсаторов соединен с источником и с другими конденсаторами точно так же, как в исходной схеме.

Вследствие равенства емкостей всех конденсаторов разность потенциалов между точками А и В равна нулю. Поэтому конденсатор 4 можно исключить (см. задачу 4). В результате получится схема, изображенная на рисунке 1.113. Она состоит из трех параллельных ветвей, две из которых содержат по два последовательно включенных конденсатора.

Общая емкость системы

Задача 6
Два маленьких шарика радиусом г несут заряды q1 и q2, различные по модулю, но одинаковые по знаку. Шарики первоначально находятся на расстоянии l друг от друга. Один из шариков закреплен. Второй шарик, удаляясь под действием электростатических сил, приобретает максимальную кинетическую энергию Wk1. Если перед началом движения второго шарика оба шарика на некоторое время были соединены проводником, то второй шарик, удаляясь, приобретает максимальную кинетическую энергию Wk2 > Wk1. Определите количество теплоты, выделившееся в проводнике при соединении шариков, и выясните, за счет какой энергии выделяется эта теплота и увеличивается кинетическая энергия второго шарика.
Решение. Согласно закрну сохранения энергии в первом случае

где Wk01 и Wp01 + W0c — начальные, a Wk1 и Wp1 + W1c — конечные значения кинетической и потенциальной энергий системы двух шариков. Причем Wp01 и W1c, — потенциальные энергии взаимодействия шариков, а W0c и W1c — их суммарные собственные энергии, одинаковые по модулю. Считая потенциальную энергию взаимодействия при бесконечно большом расстоянии между шариками равной нулю и учитывая, что Wk01 = 0, получим:


Нетрудно видеть, что действительно Wk2 > Wk1. Кроме того, в проводнике выделяется количество теплоты Q. Однако, разумеется, полная энергия должна сохраняться. Увеличение кинетической энергии и выделение теплоты во втором случае происходит за счет уменьшения собственной потенциальной энергии заряженных шариков при их соединении.
С учетом собственной энергии шариков конечную энергию в первом случае можно представить в виде

— собственная энергия шариков. Конечную энергию во втором случае запишем так:


Количество выделенной теплоты равно:
Упражнение 4
1. Пластины заряженного конденсатора попеременно заземляются. Будет ли при этом конденсатор разряжаться?
2. Плоский конденсатор, расстояние между обкладками которого d1 = 10 мм, зарядили до разности потенциалов U1 = 100 В, а затем отключили от сети. Определите разность потенциалов U2 между обкладками конденсатора, если их раздвинули до расстояния d2 = 20 мм.
3. Определите емкость конденсатора, площадь пластин которого равна S, а расстояние между пластинами d, если пластины погружены вертикально в жидкий диэлектрик до середины. Диэлектрическая проницаемость диэлектрика равна е.
4. В конденсатор емкостью C0 внесли диэлектрическую пластинку с диэлектрической проницаемостью ε = 2. Пластинку расположили так, как указано на рисунке 1.114. Определите, во сколько раз изменилась емкость конденсатора при внесении в него пластинки. Площадь пластинки в 2 раза меньше площади обкладки конденсатора, а ее толщина в 2 раза меньше расстояния между обкладками.

5. Плоский конденсатор, пространство между пластинами которого заполнено керосином (ε = 2), расположен вертикально, заряжен и отключен от источника напряжения. Напряженность электрического поля при этом в керосине Е = 20 кВ/см. Из-за дефекта в корпусе конденсатора керосин начинает вытекать, а его место занимает воздух. Предельная напряженность электрического поля в воздухе, при которой наступает электрический пробой (разряд), Епр = 30 кВ/см. Какая доля δ керосина вытечет из конденсатора к моменту пробоя конденсатора?
6. Оцените приближенно электрическую емкость тела человека.
7. Найдите емкость металлического шара радиусом r, окруженного прилегающим концентрическим слоем диэлектрика с внешним радиусом R и диэлектрической проницаемостью ε.
8. К пластинам плоского конденсатора, находящимся на расстоянии d = 1 см друг от друга, приложена разность потенциалов U = 300 В. В пространство между пластинами помещается плоскопараллельная пластина из стекла толщиной d1 = 0,3 см и плоскопараллельная пластина из парафина толщиной d2 = 0,7 см. Найдите напряжения между поверхностями стеклянной и парафиновой пластин. Диэлектрические проницаемости стекла и парафина соответственно равны ε1 = б и ε2 = 2,6.
9. Определите емкость конденсатора с трехслойным диэлектриком, диэлектрические проницаемости слоев равны ε1, ε2, ε1 (рис. 1.115). Толщина каждого диэлектрика (слоя) равна d. Площадь пластин S.

10. Четыре одинаковые металлические пластины расположены в воздухе на равных расстояниях d друг от друга (d мало по сравнению с размерами пластин). Площадь каждой из пластин равна S. Пластина 1 соединена проводником с пластиной 3, а от пластин 2 и 4 сделаны выводы (рис. 1.116). Определите емкость С такого конденсатора.

11. Определите емкость С батареи конденсаторов, схематически изображенной на рисунке 1.117. У каждого конденсатора указано значение его емкости, выраженное в микрофарадах.

12. Из проволоки сделан куб, в каждое ребро которого включено по одному конденсатору емкостью С (рис. 1.118). Найдите емкость получившейся батареи конденсаторов, если она включается в цепь проводниками, присоединенными к вершинам А и В куба.

13. Имеется N точек в пространстве. Между каждой парой точек включен конденсатор емкостью С. Найдите емкость образовавшейся батареи конденсаторов, если она включается в цепь выводами, присоединенными к двум произвольным точкам.
14. Плоский конденсатор емкостью С = 15 пФ зарядили до разности потенциалов U = 100 В, затем отключили от источника и погрузили полностью в жидкий диэлектрик (ε = 1,5). Определите изменение энергии конденсатора ΔWp.
15. Три конденсатора емкостью С = 1 мкФ каждый соединены последовательно. Конденсаторы зарядили и отключили от источника. Заряд этой батареи q = 10 -4 Кл. Затем пространство между обкладками одного из конденсаторов заполнили диэлектриком с диэлектрической проницаемостью ε = 2. Найдите энергию, запасенную в электрическом поле этих конденсаторов, и напряжение на зажимах батареи после заполнения диэлектриком одного из конденсаторов.
16. Энергия заряженного плоского конденсатора, заполненного диэлектриком, равна Wp = 2 • 10 -5 Дж. После отключения конденсатора от источника напряжения диэлектрик из конденсатора вынули, совершив при этом работу А = 7 • 10 -5 Дж. Найдите диэлектрическую проницаемость диэлектрика.
17. Сделаем в пластинах плоского конденсатора два малых отверстия — одно напротив другого. Пусть через одно из отверстий в заряженный конденсатор влетает с небольшой начальной скоростью частица так, чтобы электрическое поле конденсатора ускоряло ее (рис. 1.119).

Пролетев через конденсатор, частица вылетает из другого отверстия, приобретая дополнительную энергию ΔWp = qU, где q — заряд частицы, а U — разность потенциалов на пластинах конденсатора. Теперь с помощью магнитного поля направление движения частицы изменяется таким образом, чтобы она снова влетела через первое отверстие в конденсатор (см. рис. 1.119). (В главе 4 вы узнаете, что сила, действующая со стороны магнитного поля на движущуюся заряженную частицу, не совершает работы.) При повторном пролете через конденсатор частица вновь приобретает дополнительную энергию ΔWp, в следующем цикле — еще ΔWp и т. д. Получается циклический ускоритель, который не нуждается в источнике энергии! Где ошибка в приведенных рассуждениях?
18. Два конденсатора емкостью С1 и C2 заряжены до разности потенциалов U1 и U2 (U1 ≠ U2). Докажите, что при параллельном соединении этих конденсаторов их общая энергия уменьшается. Объясните, почему происходит уменьшение энергии.
19. Две прямоугольные пластины длиной l и площадью S расположены параллельно друг другу на расстоянии d (плоский конденсатор). Пластины заряжены до разности потенциалов U. В пространство между пластинами втягивается диэлектрик с диэлектрической проницаемостью ε. Толщина диэлектрика равна d, его ширина равна ширине пластин, а длина больше l (рис. 1.120). Трение отсутствует. Найдите зависимость силы, действующей на диэлектрик со стороны поля, от расстояния х.

20. Решите задачу 19 при условии, что разность потенциалов между пластинами поддерживается постоянной и равной U.
Мы потратили довольно много времени на изучение электричества, а рассмотрели лишь простейший частный случай неподвижных заряженных тел — электростатику. Может быть, не стоило уделять электростатике такое больпюе внимание? Нет, стоило! Мы ввели важнейшие понятия, используемые во всей электродинамике: «электрический заряд», «электрическое поле», «потенциал» и «разность потенциалов», «электрическая емкость», «энергия электрического поля». На простом частном случае выяснить суть этих фундаментальных понятий не так трудно, как в общем случае движущихся зарядов.
Теперь перейдем к изучению электромагнитных процессов, наблюдаемых при движении заряженных частиц.
1.4. Электрические поля двух противоположно заряженных тел. Электрическая емкость.
Рассмотрим систему из двух одинаковых металлических шаров радиусом R, имеющих одинаковые заряды q противоположного знака, с расстоянием между центрами шаров 2d. Между ними существует электрическое поле, которое можно характеризовать векторами напряженности электрического поля E, электрической индукции D и разностью потенциалов U. Для определения связи между разностью потенциалов и величиной заряда рассмотрим напряженность электрического поля на линии, соединяющей два заряженных шара (ось x). Она может быть определена на основе принципа суперпозиций. Напряженности от 1 и 2 шара будут направлены в одну сторону от положительно заряженного шара к отрицательно заряженному шару. Пусть начало координат лежит в точке, расположенной на одинаковых расстояниях от центров двух шаров. Тогда напряженность в точке с координатой x можно определить по выражению
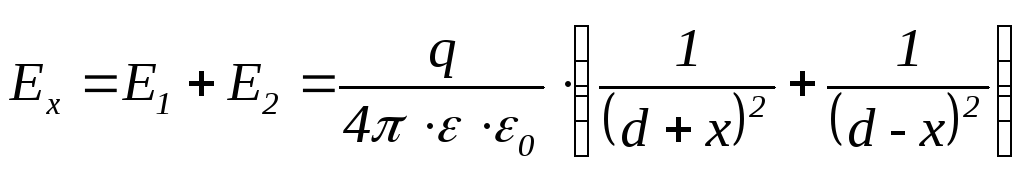
. (21)
Разность потенциалов (напряжение) между шарами можно определить по (6)
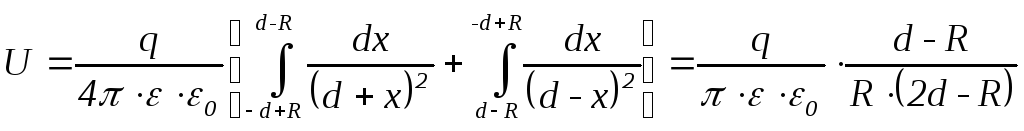
(22)
Емкость между двумя шарами можно найти по выражению
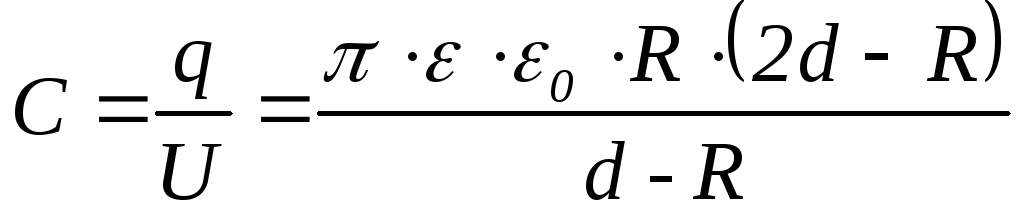
(23)
1.4.2. Два заряженных металлических цилиндра.
Рассмотрим систему из двух одинаковых металлических цилиндрических проводников радиусом R, имеющих одинаковые заряды q противоположного знака, с расстоянием между осями проводников 2d. Между ними существует электрическое поле, которое можно характеризовать векторами напряженности электрического поля E, электрической индукции D и разностью потенциалов U. Для определения связи между разностью потенциалов и величиной заряда рассмотрим напряженность электрического поля на линии, соединяющей оси заряженных проводников (ось x). Она может быть определена на основе принципа суперпозиций. Напряженности от 1 и 2 шара будут направлены в одну сторону от положительно заряженного проводника к отрицательно заряженному проводнику. Пусть начало координат лежит в точке, расположенной на одинаковых расстояниях от оси двух проводников. Тогда напряженность в точке с координатой x можно определить по выражению
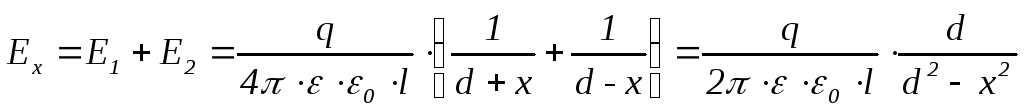
. (24)
Разность потенциалов (напряжение) между проводниками можно определить по (6)
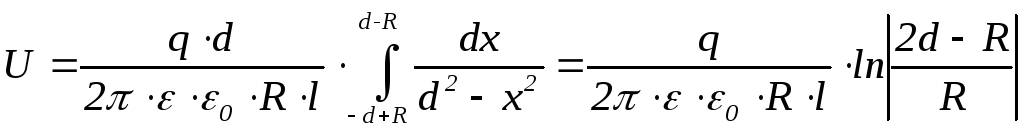
(25)
Удельная емкость (на единицу длины) между двумя проводниками можно найти по выражению
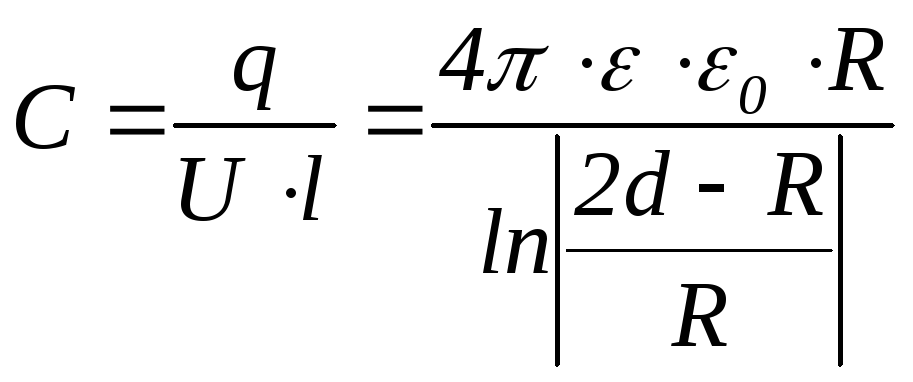
(26)
1.4.3. Система коаксиальных проводников.
Рассмотрим систему из двух заряженных коаксиально расположенных цилиндрических проводников внутреннего и внешнего. Проводники несут противоположные по знаку и одинаковые по величине заряды с линейной плотностью ρ. Внутренний проводник системы с внешним радиусом R1 может быть сплошным или полым. Внешний проводник должен быть полым с радиусами внутренним R2 и внешним R3. Между проводниками существует электрическое поле, которое можно характеризовать векторами напряженности электрического поля E, электрической индукции D и разностью потенциалов U. Внешнее электрическое поле такой симметричной системы отсутствует, Для определения связи между разностью потенциалов между проводниками и величиной заряда рассмотрим напряженность электрического поля вдоль радиальной линии с центром на общей оси внутреннего и внешнего проводников. Т.к. мы рассматриваем металлические проводники, то электрических полей внутри проводников не будет. Для рассмотрения электрического поля между проводниками достаточно рассмотреть поле внутреннего цилиндрического проводника, которое описывается выражениями (16). Для напряжения между двумя проводниками можно записать
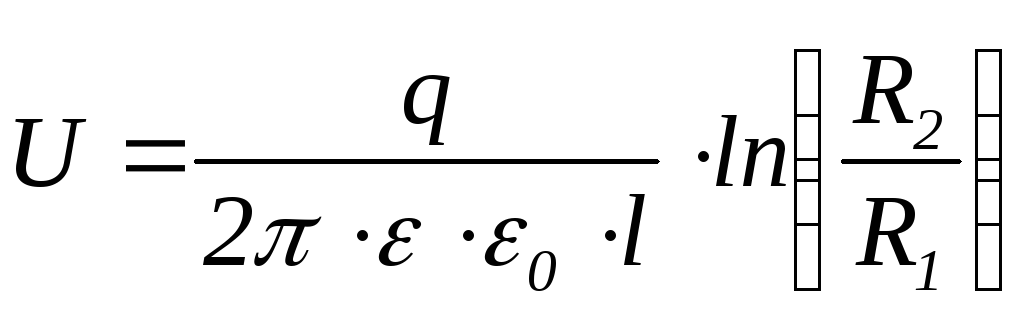
. (27)
Удельную емкость (на единицу длины) между двумя проводниками можно найти по выражению
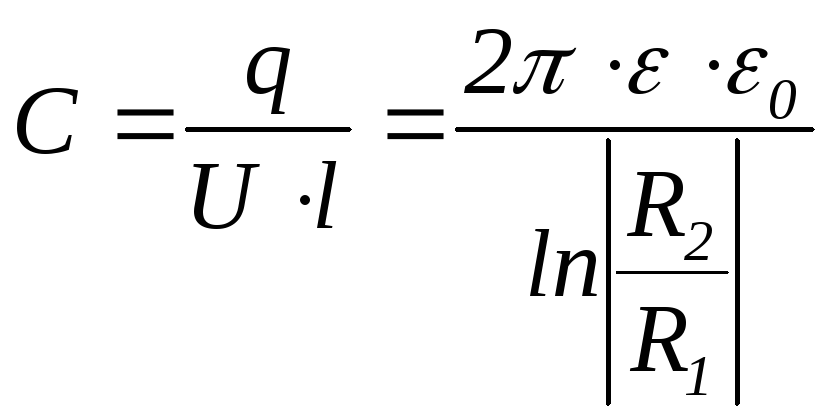
(28)
Задачник Горбатый Овчинников
6. Во сколько раз емкость некоторого уединенного проводника больше емкости его уменьшенной в 2 раза копии?
ответ зависит от формы проводника
7. Если вблизи проводящего шара, расположенного вдали от других заряженных тел, поместить незаряженный проводник произвольной формы, то емкость шара:
8. Если вблизи проводника, расположенного вдали от других заряженных тел,
поместить незаряженный стеклянный шар, то емкость проводника:
9. Вблизи положительно заряженного проводящего шара закреплен точечный положительный заряд. Если заряд шара увеличить в 2 раза, то его потенциал увеличится:
Б) более, чем в 2 раза
В) менее, чем в 2 раза
10. Почему не принято говорить о емкости проводника, вблизи которого расположены другие заряженные тела?
11. Укажите ошибочные утверждения:
пропорциональности между зарядом положительной
обкладки и разностью потенциалов между
формулой C 0 S / d
Если расстояние между обкладками плоского
напряжения, уменьшить в два раза, то напряжение на
конденсаторе не изменится, а заряд увеличится в два
Если пространство между обкладками плоского
конденсатора, заряженного и отключенного от
источника напряжения, заполнить диэлектриком с
проницаемостью , то заряд конденсатора не
изменится, а напряжение на нем уменьшится в раз
соединить последовательно и подключить к
источнику напряжения, то на конденсаторах
установятся одинаковые заряды, а напряжение будет
большим на том конденсаторе, емкость которого
подключить к источнику напряжения, то на
конденсаторах установятся одинаковые напряжения,
а заряд будет большим у того конденсатора, емкость
Если к заряженному конденсатору емкостью C 1
подключить заряженный конденсатор емкостью C 2 ,
как показано на рис. 7.1, то напряжения и заряды
конденсаторов не изменятся
как показано на рис. 7.2, то напряжения на
конденсаторах станут одинаковыми, а суммарный
заряд обкладок, которые соединили, не изменится
7.1. Найдите емкость шарового проводника радиуса R 1 = 100 мм, окруженного прилегающим к нему концентрическим слоем диэлектрика проницаемости = 6 и
наружного радиуса R 2 = 200 мм.
7.2. Найдите емкость металлического шара радиуса R , окруженного концентрическим с ним незаряженным шаровым проводящим слоем. Радиусы сферических поверхностей слоя равны a и b .
7.3. Между обкладками плоского воздушного конденсатора поместили параллельно им стеклянную пластину, толщина которой в 2 раза меньше расстояния между обкладками. Во сколько раз увеличилась при этом емкость конденсатора.
Диэлектрическая проницаемость стекла .
7.4. Расстояние между обкладками плоского конденсатора равно d . Определите емкость конденсатора, если известно, что при заряде конденсатора q напряженность поля в конденсаторе равна E .
7.5. Пространство между обкладками плоского конденсатора представляет собой три параллельных слоя толщинами d , 2 d и d . Проницаемости диэлектрических слоев указаны на рис. 7.3, слои проводников показаны штриховкой, площадь каждой обкладки конденсатора S . Найдите емкость С конденсатора для случаев а) - г),
показанных на рисунке.
7.6. Зазор между обкладками плоского конденсатора заполнен диэлектриком,
проницаемость которого меняется в перпендикулярном обкладкам направлении – растет линейно от 1 до 2 . Площадь каждой обкладки S , расстояние между ними d .
Найдите емкость C конденсатора.
7.7. Пространство между обкладками плоского конденсатора заполнено диэлектриком, проницаемость которого зависит от расстояния x до одной из обкладок
d - расстояние между обкладками.
Площадь каждой обкладки S . Найдите емкость C
7.8. Определите емкость C плоского конденсатора, заполненного неоднородным диэлектриком, если известно, что напряженность поля в диэлектрике зависит от
координаты x по закону E q ( x 2 ) , где q – заряд конденсатора, и - постоянные,
ось X перпендикулярна обкладкам, x = 0 на одной из обкладок. Расстояние между обкладками d .
7.9. Найдите емкость C сферического конденсатора, радиусы обкладок которого
проницаемость которого зависит от расстояния r до центра конденсатора как r ,
7.10. Найдите емкость C сферического конденсатора, радиусы обкладок которого a и b , причем a < b , если пространство между обкладками заполнено
диэлектриком, проницаемость которого зависит от расстояния
конденсатора как / r , где const .
7.11. Определите емкость сферического конденсатора, заполненного неоднородным диэлектриком, если известно, что напряженность поля в диэлектрике
зависит от расстояния r до центра конденсатора по закону E q r 3 , где q – заряд конденсатора, - постоянная. Радиусы обкладок конденсатора a и b ( a < b ).
7.12. Найдите емкость С двухслойного цилиндрического конденсатора, радиусы обкладок которого a и 3 a , а пространство между обкладками заполнено двумя цилиндрическими слоями диэлектриков с проницаемостями и 2 . Толщина каждого слоя равна a, длина конденсатора l велика по сравнению с а .
7.14. Определите емкость C цилиндрического конденсатора, заполненного неоднородным диэлектриком, если известно, что напряженность поля в диэлектрике
зависит от расстояния r от оси конденсатора по закону E q r 2 , где q – заряд конденсатора, - постоянная. Радиусы обкладок конденсатора a и b ( a < b ).
7.15. Найдите емкость C цилиндрического конденсатора длины l , радиусы
заполнено диэлектриком, проницаемость которого зависит от расстояния r до оси конденсатора как / r , где .
Взаимная емкость проводников
7.16. Два длинных прямых провода одинакового радиуса сечения a
расположены в воздухе параллельно друг другу. Расстояние между осями проводов равно b . Найдите взаимную емкость проводов C 1 на единицу их длины при условии a b . Вычислите C 1 , если a = 1 мм и b = 50 мм.
7.17. Найдите взаимную емкость C системы из двух одинаковых металлических шаров радиуса a , расстояние между центрами которых b , причем a b . Система находится в однородном диэлектрике проницаемости .
7.18. Два одинаковых воздушных конденсатора соединили параллельно,
зарядили до напряжения U 1 = 30 В и отключили от источника. Затем пространство между обкладками одного конденсатора заполнили диэлектриком с диэлектрической проницаемостью = 2. Какое напряжение U 2 установилось на конденсаторах?
7.19. К источнику напряжения U = 100 В подключили последовательно два одинаковых конденсатора, каждый емкостью C = 40 пФ. Затем один из них заполнили диэлектриком проницаемости = 3. Во сколько раз уменьшилась напряженность электрического поля в этом конденсаторе? Какой заряд q пройдет в цепи?
§ 1.24. Электрическая емкость
Такого рода задачи встречаются очень часто не только в электростатике, но и при изучении электрического тока. Для их решения вводят особую физическую величину — электрическую емкость, или просто емкость.
Электрическая емкость уединечного проводника
Рассмотрим сферический проводник радиусом r. Пусть он находится очень далеко от других тел, так что его размеры во много раз меньше расстояний до этих тел. Такой проводник называют уединенным.
не зависит от заряда и определяется лишь радиусом шара и диэлектрической проницаемостью е окружающей среды.
Замечательным является то, что не только для шара, но и для уединенного проводника произвольной формы потенциал прямо пропорционален заряду. Поэтому отношение заряда проводника к его потенциалу не зависит, от значения заряда и определяется лишь геометрическими размерами проводника, его формой и электрическими свойствами окружающей среды (диэлектрической проницаемостью ε). Это позволяет ввести понятие электрической емкости уединенного проводника.
Электрической емкостью С проводника называется отношение заряда q проводника к его потенциалу φ:
Емкость выражается через отношение заряда к потенциалу, но не зависит ни от того, ни от другого. Точно так же, например, скорость при равномерном прямолинейном движении выражается через отношение пути ко времени:Емкость не зависит от материала проводника: железные, медные тела и тела из других материалов одинаковых размеров и формы имеют одинаковую емкость.
Практическая польза понятия емкости состоит в том, что, определив емкость проводника экспериментально или вычислив ее теоретически, можно с помощью формулы (1.24.2) найти потенциал проводника по известному заряду или, наоборот, заряд по известному потенциалу.
Емкость шара
Согласно определению емкости (1.24.2) и формуле (1.24.1) электрическая емкость шара в СИ равна:

В системе СГСЭ потенциал шара вычисляется по формуле (1.19.4), тогда при k = 1 и в соответствии с определением (1.24.2)
В вакууме емкость проводящего шара в системе СГСЭ равна его радиусу.
Зависимость емкости проводника от окружающих тел
В действительности ни один проводник не является, строго говоря, уединенным. Вблизи любого заряженного тела находятся те или иные предметы. И в этих случаях можно говорить об электрической емкости проводника, но она будет зависеть от расположения окружающих тел. В этом можно убедиться на опыте.
Возьмем электрометр и заземлим его корпус. К стержню электрометра прикрепим полый металлический шар с отверстием. Сообщим электрометру заряд q с помощью маленького металлического шарика на изолирующей ручке. Для этого коснемся заряженным шариком внутренней поверхности сферы (рис, 1.96, а). Весь заряд шарика при этом перейдет к электрометру. Возникает разность потенциалов между стержнем электрометра и землей, и его стрелка отклоняется. Сообщим электрометру еще такой же заряд* q. Потенциал стержня относительно земли возрастает в 2 раза. Следовательно, отношение заряда к потенциалу постоянно и равно емкости металлического шара со стержнем.

Но стоит поднести к шару ладони рук (не касаясь его), как стрелка электрометра приблизится к вертикали. Потенциал шара уменьшается, и, значит, емкость возрастает. Такой же эффект наблюдается при поднесении незаряженного диэлектрика к диску на стержне электрометра (см. § 1.14).
Почему это происходит? Потенциал проводника определяется не только зарядом на его поверхности. Согласно принципу суперпозиции (1.19.5) потенциал поля в некоторой точке равен сумме потенциалов, создаваемых всеми заряженными телами. Незаряженные тела также влияют на потенциал проводника, так как под действием поля шара на поверхностях проводников появляются свободные заряды противоположных знаков (вследствие электростатической индукции), а у диэлектриков — связанные заряды (вследствие поляризации).
С помощью электрометра можно обнаружить зависимость емкости проводника от его размеров. Укрепим на стержне полый шар меньшего радиуса. Если теперь сообщить ему такой же заряд q, как и в первом опыте, то потенциал стержня оказывается большим (рис. 1.96, б). Это означает уменьшение емкости с уменьшением размера шара.
Единицы электроемкости
Формула (1.24.2) позволяет ввести единицы электроемкости. В СИ единицей емкости является фарад (Ф).
В системе СГСЭ за единицу емкости в соответствии с формулой (1.24.4) принимают емкость шара радиусом 1 см в вакууме. Эта единица — сантиметр.
Нетрудно видеть, что

Емкость в 1 Ф очень велика. Уединенный шар, обладающий такой емкостью, имел бы радиус, в 13 раз превышающий радиус Солнца. Поэтому на практике часто используют доли этой единицы: микрофарад (мкФ) — 10 16 Ф и пикофарад (пФ) — 10 -12 ф Емкость земного шара равна 709 мкФ.
Формула (1.24.3) позволяет выразить электрическую постоянную ε0 через емкость и размеры проводника:
Это означает, что электрическую постоянную можно выражать в фарадах на метр (Ф/м).
* Два одинаковых заряда можно получить, например, так: коснуться двумя одинаковыми шариками на изолирующей ручке большого заряженного шара и одновременно отвести от шара.
Читайте также:
