На полу лифта расположены два одинаковых металлических бака керосин
Решение.
Из графика видно, что скорость линейно возрастает со временем. Это означает, что тело движется с постоянным ускорением, равным a= ∆𝑣 ∆𝑡 . Из графика видно, что за время ∆t=2 секунды тело приобрело скорость ∆v=15 м/с, следовательно, ускорение равно
a=15/2=7,5 м/с2.
Задание 2. При исследовании зависимости силы трения скольжения Fтр деревянного бруска по горизонтальной поверхности стола от массы m бруска получен график, представленный на рисунке. Согласно графику в этом исследовании коэффициент трения равен
Решение.
Из графика видно, что при массе бруска m=0,25 кг сила трения равнялась F=0,8 Н. Учитывая, что сила трения это F=μN=μmg , найдем коэффициент трения как
μ=F/mg=0,8/0,25*10=0,32
Задание 3. Легковой автомобиль и грузовик движутся по мосту. Масса легкового автомобиля m = 1000 кг. Какова масса грузовика, если отношение значений потенциальной энергии грузовика и легкового автомобиля относительно уровня воды равно 4?
Решение.
Потенциальная энергия автомобиля массой m=1000 кг относительно уровня воды h, равна E1=mgh Потенциальная энергия грузовика массой M относительно того же уровня воды h, равна E2=Mgh
Так как E2/E1=4
имеем: Mgh/mgh=M/m=4
и масса грузовика равна M=4m=4000 кг.
Задание 4. Груз массой 200 г, подвешенный на пружине, совершает свободные вертикальные колебания с частотой 4 Гц. С какой частотой будет совершать такие колебания груз 50 г, если его подвесить на ту же пружину?
Решение.
Частота колебаний v=4 Гц пружинного маятника массой m=200 г = 0,2 кг определяется по формуле
v= 𝟏 𝟐π 𝒌 𝒎
где k – жесткость пружины. Если взять маятник массой m2=50 г = m/4, то частота колебаний станет равной
v2= 𝟏 𝟐π 𝒌 𝒎/𝟒 =2*1/2π 𝒌/𝒎 =2v
v2=2*4=8 Гц
Задание 5. На полу лифта расположены два одинаковых металлических бака, в которых доверху налит керосин (см. рисунок).
Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
1) Давление керосина на дно первого бака в 2 раза больше, чем на дно второго.
2) Оба бака давят на пол лифта с одинаковой силой.
3) Силы давления керосина на дно первого и второго баков одинаковы.
4) Оба бака оказывают на пол лифта одинаковое давление.
5) Если лифт начнёт движение вниз с ускорением 3 м/с2, давление керосина на дно баков увеличится на 30 %.
Давление керосина на дно первого бака равно P1=F/S=mg/2a^2, где m - масса керосина. Давление на дно второго бака P2=mg/a^2. Видно, что давление P2=2P1, следовательно, давление керосина на дно первого бака в 2 раза меньше, чем на дно второго бака.
2) Так как баки одинаковы, то их массы равны. Объем первого бака равен М1=2a*a*a=2a^3, объем второго бака V2=2a*a*a=2a^3. Тогда масса керосина в каждом баке будут равны m=pV1=pV2. Имеем два тела одинаковой массы, которые будут давить на дно лифта с равной силой F=mg.
3) Так как масса керосина в обоих баках одинакова, то керосин будет давить на дно этих баков с силой F=mg, где m – масса керосина.
4) Давление бака на пол лифта обратно пропорционально площади основания бака. Площадь основания первого бака равна S1=2a^2, а площадь второго бака S2=a^2 , то есть первый бак будет оказывать давление в 2 раза меньше, чем второй бак.
5) При движении лифта вниз с ускорением a=3 м/с2, оно будет компенсировать ускорение свободного падения g, то есть керосин будет иметь ускорение свободного падения g-a м/с2. В результате его давление на дно баков уменьшится.
Ответ: 23.
Задание 7. В момент t = 0 мячик бросают с начальной скоростью v0 под углом α к горизонту с балкона высотой h (см. рисунок). Сопротивлением воздуха пренебречь. Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) координата х мячика
2) проекция скорости мячика на ось х
3) проекция ускорения мячика на ось у
4) координата y мячика
Решение.
1) Проекция координаты x тела, брошенного под углом к горизонту, линейно возрастает со временем. Этому не соответствует ни один из графиков.
2) При движении тела под углом к горизонту его горизонтальная проекция скорости . Этому соответствует график под буквой Б.
3) Ускорение мячика на ось y равно ускорению свободного падения g, сначала с отрицательным знаком, а затем, с положительным.
4) Координата y мячика сначала плавно возрастает, а затем, убывает со все возрастающей скоростью. Этому соответствует график под буквой А.
Ответ: 42.
Задание 8. При уменьшении абсолютной температуры на 600 К среднеквадратичная скорость теплового движения молекул неона уменьшилась в 2 раза. Какова начальная температура газа?
Задание 9. Какую работу совершил газ в процессе, изображённом на pV-диаграмме (см. рисунок)?
Площадь данной трапеции можно найти по формуле
A=1/2(P1+P2)*(V1-V2)
P1=0,2*10^5
P2=0,05*10^5
V1=0,05
V2=0,25
A=1/2*0,25*10^5*0,2=2500 Дж
2,5кДж
Задание 10. Определите, каково должно быть примерное отношение масс mfe/mal железного и алюминиевого тел, чтобы при получении одного и того же количества теплоты они нагрелись на одно и то же число градусов. Ответ округлите до целых.
Решение.
Количество теплоты Q, необходимое для изменения температуры тела на ∆T градусов, определяется выражением: Qfe=Cfemfe∆T
где Cfe=460 Дж/кг*К- удельная теплоемкость железа. Аналогично для алюминия:Qal=Calmal∆T
Cal=900Дж/кг*К
Qfe=Qa
Cfemfe∆T=Calmal∆T
mfe/mal= Cal∆T/Cfe∆T=900/460=(приблизительно)2
Задание 11. Один моль идеального одноатомного газа совершает циклический процесс 1-2-3-4-1, график которого показан на рисунке в координатах p-V. Из предложенного перечня утверждений выберите два правильных и укажите их номера.
1) В процессе 1-2 газ совершает отрицательную работу.
2) В процессе 2-3 газу сообщают положительное количество теплоты.
3) В процессе 3-4 газ отдаёт положительное количество теплоты в окружающую среду.
4) В процессе 4-1 внутренняя энергия газа остаётся неизменной.
5) Работа, совершённая газом в процессе 1-2, в 1,6 раза больше работы, совершённой над газом в процессе 3-4.
Решение. 1) В процессе 1-2 имеем постоянное давление p и изменение объема∆V>0 следовательно, газ совершает работу A=p∆V>0
2) В процессе 2-3 давление газа уменьшается при постоянном объеме. Из уравнения состояния идеального газа PV/T=const при постоянном объеме следует, что при уменьшении давления температура T также должна уменьшаться.
3) В процессе 3-4 давление постоянно, а объем уменьшается, следовательно, из уравнения V/T=const имеем уменьшение температуры, то есть газ отдает свое тепло.
4) Процесс 4-1увеличение объема должно приводить к увеличению температуры, и внутренняя энергия газа возрастает.
5) Работа газа, совершенная в процессе 1-2 – это площадь под кривой 1-2, а работа в процессе 3-4 – площадь под кривой 3-4. Первая площадь равна A1=p∆V=4*4=16 клеток. Вторая площадь A2=5*2=10 клеток. И отношение работ, равно A1/A2=16/10=1,6 То есть работа в процессе 1-2 в 1,6 раз больше работы в процессе 3-4.
Ответ: 35.
Задание 12. На рисунке изображена диаграмма четырёх последовательных изменений состояния 2 моль идеального газа. Какие процессы связаны с наименьшими положительными значениями работы газа и работы внешних сил? Установите соответствие между такими процессами и номерами процессов на диаграмме.
ПРОЦЕССЫ
А) работа газа положительна и минимальна
Б) работа внешних сил положительна и минимальна
НОМЕРА ПРОЦЕССОВ
1) 1
2) 2
3) 3
4) 4
Решение.
А) Работа газа, равная A=p∆V положительна, когда объем газа возрастает. Объем газа возрастает в процессе 3 и 4. При этом величина работы газа будет равна площади под этими участками
Из рисунка видно, что синяя площадь меньше красной, следовательно, работа газа на участке 3 меньше работы газа на участке 4.
Б) Работа внешних сил возникает при уменьшении объема газа – это участки 1 и 2. По аналогии с п. А видно, что работа внешних сил минимальна на участке 1.
Ответ: 31.
Задание 13. На рисунке изображён длинный прямой цилиндрический проводник, по которому течёт электрический ток. Направление тока указано стрелкой. Как направлен (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) вектор магнитной индукции поля этого тока в точке С? Ответ запишите словом (словами).
Решение.
Вектор магнитной индукции направлен по касательной к линия магнитного поля, возникающего вокруг проводника с током. Определим сначала направление линий магнитного поля по правилу буравчика. Буравчик направляем вдоль движения тока и крутим ручку буравчика так, чтобы он ввинчивался по направлению движения тока. Получаем, что линии магнитного поля направлены по часовой стрелке (сверху вниз по кругу вокруг проводника). Тогда в точке C касательная к линиям магнитного поля будет направлена к наблюдателю.
Ответ: к наблюдателю.
Задание 14. Каждый из резисторов в схеме, изображённой на рисунке, имеет сопротивление 150 Ом. Каким будет сопротивление участка цепи, если ключ К замкнуть?
Решение.
При замыкании ключа К весь ток потечет через него, так как ток идет по пути наименьшего сопротивления. В итоге, в цепи остается только первый резистор, сопротивлением 150 Ом.
Ответ: 150.
Задание 15. Если ключ К находится в положении 1, то период собственных электромагнитных колебаний в контуре (см. рисунок) равен 3 мс. Насколько увеличится период собственных электромагнитных колебаний в контуре, если ключ перевести из положения 1 в положение 2?
Решение: T=2π 𝑳𝑪
При переключении ключа емкость конденсатора становится равной 4C и период становится равным:
T2=2π 𝟒𝑳𝑪 =2*2π 𝑳𝑪 =2T
увеличивается в 2 раза и составляет T=2*3=6 мс. В результате период колебаний увеличится на T2-T=6-3=3мс
Задание 16. При нагревании спирали лампы накаливания протекающим по ней электрическим током основная часть подводимой энергии теряется в виде теплового излучения. На рисунке изображены графики зависимости мощности тепловых потерь лампы от температуры спирали Р = Р(Т) и силы тока от приложенного напряжения I = I(U).
Выберите два верных утверждения о физических величинах, характеризующих этот процесс.
1) При напряжении на лампе 80 В тепловая мощность, выделяемая на лампе, равна 80 Вт.
2) При мощности тепловых потерь 150 Вт температура нити накала лампы менее 3000 К.
3) При силе тока через лампу 2 А температура нити накала составляет около 3600 К.
4) С увеличением силы тока через лампу температура её спирали увеличивается.
5) При мощности тепловых потерь 100 Вт напряжение на лампе составляет 100 В.
2) Из левого графика видно, что при P=150 Вт температура накала нити лампы больше 3000 К.
3) При I=2 А напряжение составляет U=100 В и мощность равна P=2*100=200 Вт. Из левого графика видно, что при такой мощности температура нити накала лампы примерно 3600 К.
4) При увеличении силы тока через лампу растет выделяемая мощность, а следовательно (левый график), растет и температура нити накала лампы.
5) При P=100 Вт напряжение равно P=U^2/R
U= 𝑷𝑹
R=U/I=100/2=50 Oм, U= 𝟏𝟎𝟎∗𝟓𝟎 =50*1,4=70
Ответ: 34.
Задание 17. Плоский конденсатор зарядили и отключили от гальванического элемента. Как изменятся при уменьшении зазора между обкладками конденсатора ёмкость конденсатора и величина заряда на его обкладках?
1) увеличится
2) уменьшится
3) не изменится
Решение.
Емкость C конденсатора зависит от расстояния d между его обкладками по формуле C= 𝜺𝟎𝑺 𝒅
где ε0- абсолютная диэлектрическая проницаемость среды между обкладками; S – площадь обкладки. Из этой формулы видно, что при уменьшении d емкость конденсатора увеличивается.
Заряд на обкладках конденсатора останется прежним, так как он был отключен от источника тока.
Ответ: 13.
Задание 18. В первой экспериментальной установке отрицательно заряженная частица влетает в однородное магнитное поле так, что вектор скорости v0 перпендикулярен индукции магнитного поля (рис. 1). Во второй экспериментальной установке вектор скорости v0 такой же частицы параллелен напряжённости электрического поля (рис. 2). Установите соответствие между экспериментальными установками и траекториями движения частиц в них.
ДВИЖЕНИЕ ЧАСТИЦЫ
А) в первой установке
Б) во второй установке
ТРАЕКТОРИЯ
Решение.
А) На частицу со стороны магнитного поля будет действовать сила Лоренца, равная
F=eνBsinα
и так как вектор скорости перпендикулярен индукции магнитного поля, то имеем sin90=1 и F=eνB
Направление силы Лоренца определяется правилом левой руки. Учитывая, что данное правило разработано для направления тока от «+» к «-», получаем направление силы Лоренца перпендикулярно направлению движения частицы (изначально она направлена вниз, так как отрицательная частица движется к положительному заряду). В результате частица будет описывать круговое движение. Ответ под номером 2.
Б) Здесь на частицу действует сила Кулона F=qE, направленная в сторону отрицательного заряда. Под действием этой силы, частица будет продолжать движение в горизонтальном направлении. Ответ под номером 1.
Ответ: 21.
Задание 19. Определите число протонов и число нейтронов в ядре изотопа криптона 𝟑𝟔 𝟖𝟖 𝑲𝒓 .
Задание 20. Какова длина волны электромагнитного излучения, в котором импульс фотонов равен 1*10^-27 кг∙м/с?
Задание 21. При исследовании зависимости кинетической энергии фотоэлектронов от частоты падающего света фотоэлемент освещался через светофильтры. В первой серии опытов использовался светофильтр, пропускающий только синий свет, а во второй — только зелёный. В каждом опыте наблюдали явление фотоэффекта и измеряли запирающее напряжение.
Как изменились частота световой волны и запирающее напряжение при переходе от первой серии опытов ко второй? Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Решение.
Изменение частоты световой волны можно найти из фразы «Каждый Охотник Желает Знать Где Сидит Фазан», в которой соответствующие цвета расположены в порядке возрастания частот. То есть синий цвет (буква С во фразе) будет иметь большую частоту, чем зеленый (буква З во фразе), то есть частота убывает от опыта к опыту.
Известно, что чем меньше частота света, тем меньшей энергией он обладает. Свет, обладающий меньшей энергией, сообщает фотоэлектронам меньшую скорость. Следовательно, для их удержания нужно меньшее запирающее напряжение. То есть запирающее напряжение будет уменьшаться от опыта к опыту.
Ответ: 22.
Задание 22. Ученик измерял силу тяжести, действующую на груз. Показания динамометра приведены на фотографии. Погрешность измерения равна цене деления динамометра.
Запишите показания динамометра с учётом погрешности измерений.
Решение.
Из рисунка видно, что одно деление динамометра равно (0,5-0):5=0,1 Н. Следовательно, динамометр показывает уровень 1,6 Н с погрешностью одного деления, то есть 0,1 Н. Получаем результаты измерений:1,6+-0,1H
Задание 23. Ученик изучает закон Архимеда, изменяя в опытах объём погружённого в жидкость тела и плотность жидкости. Какие два опыта он должен выбрать, чтобы обнаружить зависимость архимедовой силы от объёма погружённого тела? (На рисунках указана плотность жидкости.)
Решение.
Чтобы определить как будет меняться сила Архимеда от объема погруженного тела, нужно выбрать жидкости с одинаковой плотностью и два тела с разными объемами. Этим условиям удовлетворяют опыты под номерами 3 и 4.
Ответ: 34.
Задание 25. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?
Решение.
Кинетическая энергия идеального газа в начальный момент времени равна
E1=3/2kT1
E2=3/2kT2
E1/E2=4, T1/T2=4→T2=1/4T1
В задаче сказано, что T1-T2=T1-1/4T1=3/4T1=600
T1=600*4/3=800K
Задание 26. В цепи, изображённой на рисунке, идеальный амперметр показывает 1 А. Найдите напряжение на резисторе R3.
Решение.
Найдем сначала силу тока, проходящего через сопротивление R3. Данный ток I в точке ветвления расщепляется на два потока: через резисторы R1 и R2 обратно пропорционально их сопротивлениям. Так как в сумме R1+R2=4 Ом, то, условно, ток делится на 4 части, и через сопротивление R1 протекает 1/4 часть тока I, а через сопротивление R2 – 3/4 части тока I. Это можно записать в виде I1=1/4 *I
где I1=1А – показание амперметра на сопротивлении R1. Отсюда получаем, что сила тока в цепи равна
I=4I1=4A
U=IR=4*5=20B
Задание 28. Снаряд массой 2 кг, летящий со скоростью 100 м/с, разрывается на два осколка. Один из осколков летит под углом 90° к первоначальному направлению. Под каким углом к этому направлению полетит второй осколок, если его масса 1 кг, а скорость 400 м/с?
P=P1+P2- по закону сохранения импульсов
Векторы импульсов до взрывов и осколки после взрыва образуют прямоугольный треугольник
Значит:
P=P2*cosα
Mv=m2v2*cosα
cosα= Mv/m2v2=2*100/1*400=0,5
cosα=60 градусов
Задание 29. Снаряд, движущийся со скоростью v0 разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая движется в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ∆E. Скорость осколка, движущегося вперёд по направлению движения снаряда, равна v1. Найдите массу m осколка.
Решение.
Введём обозначение: v2 — модуль скорости летящего назад осколка снаряда. Система уравнений для решения задачи:
Краткое описание документа:
Задание 1. Используя график зависимости модуля скорости тела от времени (см. рисунок), определите ускорение прямолинейно движущегося тела в момент времени t = 1 с.
Задание 2. При исследовании зависимости силы трения скольжения Fтр деревянного бруска по горизонтальной поверхности стола от массы m бруска получен график, представленный на рисунке. Согласно графику в этом исследовании коэффициент трения равен
Рабочие листы и материалы для учителей и воспитателей
Более 3 000 дидактических материалов для школьного и домашнего обучения
На полу лифта расположены два одинаковых металлических бака керосин

Квадратная рамка со стороной а=4см находится в однородном магнитном поле с индукцией. Плоскость рамки расположена под углом в 60 градусов к линиям индукции. Индукция меняется со временем по закону B=5t^2+2 Тл, определите эдс индукции в момент времени t=2c



Бексултан,
Начальный импульс системы "винтовка+пуля" равен нулю. Проекция полного импульса этой системы на горизонтальное направление сохраняется. Импульс винтовки, полученный при отдаче, численно равен импульсу пули

Это сложно решить?)
Для оптимизации производственного процесса сборочный конвейер движется так, что
закон движения собираемого агрегата имеет вид x =At - Bsin*wt , где A = 0,5 м/с, B = 0,25
м, w = 2 с-1. Найти максимальную скорость агрегата. Построить графики зависимостей
координаты и скорости агрегата от времени.



Миша, опустить байку про агрегат, получится обычная задача "точка движется по кинематическому закону. ". Взять производную по времени, получится скорость точки. В сети полно графопостроителей в онлайн режиме, а можно и скачать, например, Grapher. График построят быстрее, чем палец от клавиатуры уберете.
Ангелина, ваша схема при произвольных параметрах достаточно громоздкая. Но, при заданных в условии значениях сопротивлений резисторов она значительно упрощается. Я думаю, что сила тока через резистор 6 равна нулю. Такой вывод можно сделать, практически не проводя расчетов. Если действовать методом суперпозиции, т.е. оставить в цепи одну батарею, а вторую закоротить, то получится мостовая схема, роль мостика играет резистор 6, и этот мост сбалансирован.

НЕ понимаю,помогите пж:Задание 5.На полу лифта расположены два одинаковых металлических бака, в которых доверху налита вода (см. рисунок).
Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
Гидростатика
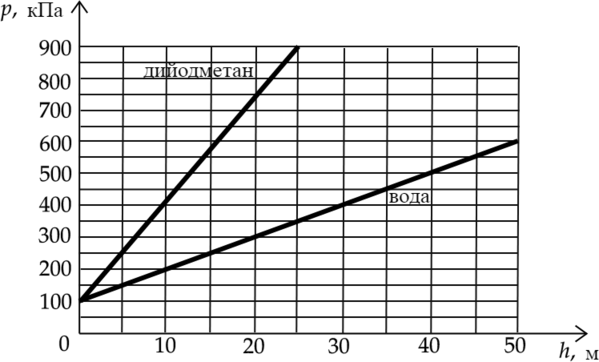
На рисунке представлены графики зависимости давления \(p\) от глубины погружения \(h\) для двух покоящихся жидкостей: воды и тяжёлой жидкости дийодметана, при постоянной температуре.
Выберите два верных утверждения, согласующихся с приведёнными графиками.
1) Если внутри пустотелого шарика давление равно атмосферному, то в воде на глубине 10 м давления на его поверхность извне и изнутри будут равны друг другу.
2) Плотность керосина 0,82 г/см \(^3\) , аналогичный график зависимости давления от глубины для керосина окажется между графиками для воды и дийодметана.
3) В воде на глубине 25 м давление p в 2,5 раза больше атмосферного.
4) С ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде.
5) Плотность оливкового масла 0,92 г/см \(^3\) , аналогичный график зависимости давления от глубины для масла окажется между графиком для воды и осью абсцисс (горизонтальной осью).
Полное давление \(p\) складывается из атмосферного давления \(p_a\) и гидростатического давления столба жидкости: \[p=\rho gh+p_a\] 1) Как видно из графика, давление воды на глубине 10 м принимает значение 200 кПа, что в два раза больше атмосферного давления (Атмосферное давление 100 кПа).
Утверждение 1 – \(\color>\)
2) Так как плотность керосина меньше чем плотность воды, то его аналогичный график окажется между графиком для воды и осью абсцисс.
Утверждение 2 – \(\color>\)
3) Давление в воде на глубине 25 м равно 350 кПа, что в 3,5 раза больше атмосферного.
Утверждение 3 – \(\color>\)
4) Так как прямая давления в дийодметане лежит выше прямой давления в воде, то это означает, что давление в дийодметане возрастает быстрее, чем в воде.
Утверждение 4 – \(\color>\)
5) Так как плотность оливкого масла меньше чем плотность воды, то его аналогичный график окажется между графиком для воды и осью абсцисс.
Утверждение 5 – \(\color>\)
К телу, имеющему внутреннюю герметичную полость, на невесомой нерастяжимой нити привязан сплошной шарик. Система «тело + шарик» плавает в сосуде с жидкостью, не касаясь стенок и дна сосуда. Плотность материала тела и шарика 1,6 г/см \(^3\) , плотность жидкости 800 кг/м \(^3\) , объём полости составляет 3/4 объёма тела, объём шарика равен 1/4 объёма тела. Исходя из условия задачи, выберите два верных утверждения.
1) Модуль силы Архимеда, действующей на тело, меньше модуля силы Архимеда, действующей на шарик.
2) Модуль силы натяжения нити равен модулю силы тяжести, действующей на шарик.
3) Модуль силы натяжения нити меньше модуля силы Архимеда, действующей на тело.
4) Модуль силы тяжести, действующей на шарик, равен модулю силы тяжести, действующей на тело.
5) Объём погружённой части тела равен четверти объёма этого тела.
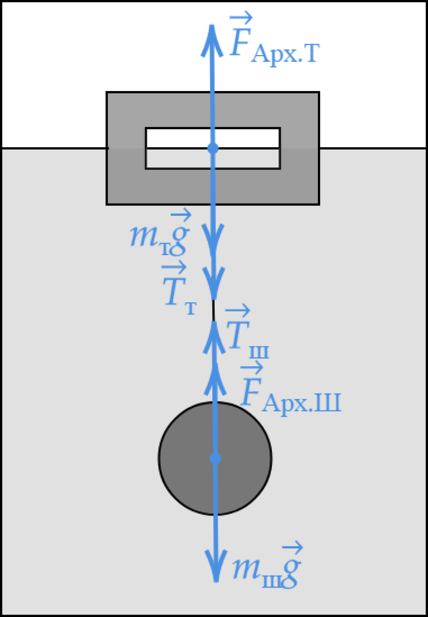
Запишем первый закон Ньютона для тела и шарика: \[F_>-m_>g-T=0\] \[F_>-m_>g+T=0\]
Сложим два уравнения: \[F_>-m_>g+F_>-m_>g=0\]
Обозначим плотность жидкости \(\rho_1\) , плотность материала \(\rho_2=2\rho_1\) \[\rho_1gV_1-\rho_2\cdot \fracV_ g+\rho_1 g \cdot \frac V_-\rho_2\cdot \frac V_ g=0\] \[\rho_1V_1-2\rho_1\cdot \fracV_ +\rho_1 \cdot \frac V_-2\rho_1\cdot \frac V_ =0\] \[V_1-2\cdot \fracV_ + \frac V_-2\cdot \frac V_ =0\] \[V_1=\fracV_T\]
Тело плавает, погруженное на 3/4 своего объёма.
1) Сила Архимеда, действующая на тело, равна \(\displaystyle F_>=\rho_1g\fracV_T\) , а сила Архимеда, действующая на шар \(\displaystyle F_>=\rho_1g\fracV_T\) .
Утверждение 1 – \(\color>\)
2) \[T=m_>g-F_>\]
Утверждение 2 – \(\color>\)
3) \[T=F_>-m_>g\]
Утверждение 3 – \(\color>\)
4) Модуль силы тяжести тела: \[m_>g=\rho_2\cdot \fracV_g\] Модуль силы тяжести шарика: \[m_>g=\rho_2\cdot \fracV_g\]
Утверждение 4 – \(\color>\)
5) Объём погружённой части тела равен \(\dfrac\) объёма этого тела.
Утверждение 5 – \(\color>\)
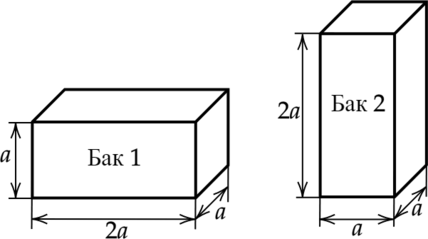
На полу лифта расположены два одинаковых металлических бака, в которых доверху налита вода (см. рисунок).
Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
1) Давление воды на дно первого бака в 4 раза меньше, чем на дно второго.
2) Первый бак давит на пол лифта с силой, в 2 раза меньшей, чем второй.
3) Сила давления воды на дно первого бака в 2 раза меньше, чем на дно второго.
4) Первый бак оказывает на пол лифта в 2 раза меньшее давление, чем второй.
5) Если лифт начнёт движение вниз с ускорением 2 м/с \(^2\) , давление воды на дно баков уменьшится на 20 %.
1) Давление воды на дно первого бака равно \[\displaystyle p_1=\frac\] где \(m\) — масса воды. Давление на дно второго бака \[\displaystyle p_2=\frac\] Видно, что давление \(p_2=2p_1\) , следовательно, давление воды на дно первого бака в 2 раза меньше, чем на дно второго бака.
Утверждение 1 – \(\color>\)
2) Сила давления равна силе тяжести воды. Так как объем одинаковый, значит масса воды в сосудах одинаковая.
Утверждение 2 – \(\color>\)
3) Утверждение 3 – \(\color>\)
4) Утверждение 4 – \(\color>\)
5) При движении лифта вниз с ускорением 2 м/с \(^2\) , оно будет компенсировать ускорение свободного падения \(g\) , то есть вода будет иметь ускорение свободного падения 10-2=8 м/с \(^2\) . В результате сила давления на дно баков будет равна \(F=8m\) .
Утверждение 5 – \(\color>\)

В сосуд с жидкостью погружают маленький датчик манометра, который регистрирует давление, создаваемое только столбом жидкости (без учёта атмосферного давления). На рисунке представлен график зависимости показаний \(p\) этого датчика давления от времени \(t\) . Известно, что датчик может либо двигаться строго по вертикали вниз со скоростью 1 мм/с, либо покоиться.
На основании анализа приведённого графика выберите два верных утверждения и укажите в ответе их номера.
1) Максимальная глубина погружения датчика давления равна 20 см.
2) В промежутке времени от 50 с до 150 с датчик давления находился на одной и той же глубине.
3) Плотность жидкости, в которую опустили датчик давления, равна 650 кг/м \(^3\) .
4) Максимальная глубина погружения датчика давления равна 15 см.
5) Плотность жидкости, в которую опустили датчик давления, равна 1300 кг/м \(^3\) .
1) Датчик двигался на промежутках от 0 с до 50 с и от 150 с до 200 с, т. е. глубина погружения \(h=1 \cdot (50 + 50 ) = 100\) мм \(= 10\) см.
Утверждение 1 – \(\color>\)
2) Из графика видно, что давление не изменяется в промежутке времени от 50 с до 150 с, это означает что датчик находился на одной и той же глубине, т. е. покоился.
Утверждение 2 – \(\color>\)
3) Давление столба жидкости: \[p=\rho gh\] Плотность жидкости: \[\rho=\frac
=\frac
Утверждение 3 – \(\color>\)
4) Глубина погружения 10 см
Утверждение 4 – \(\color>\)
5) Плотность жидкости \(\rho=1300\) кг/м \(^3\)
Утверждение 5 – \(\color>\)
Ученик помещал цилиндр, не удерживая его, в различные жидкости, плотности которых представлены в таблице, и измерял объем погруженной в жидкость части цилиндра \(V_\text< погр>\) . По результатам измерений он получил зависимость, представленную на графике объема погруженной части цилиндра \(V_\text\) от плотности жидкости \(\rho\) . Объем цилиндра постоянен и равен \(V=10\) см \(^3\)
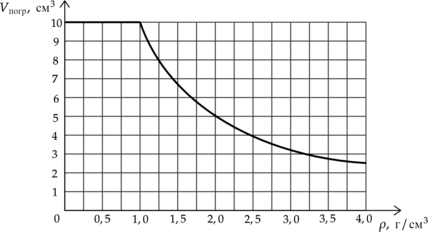
\[\begin <|c|c|c|c|c|c|c|c|>\hline \text&\text&\text&\text&\text&\text&\text&\text\\ \hline \text&0,71&0,79&1,0&1,26&1,49&2,89&3,25\\ \hline \end\]
На основании анализа приведённого графика выберите два верных утверждения и укажите в ответе их номера.
1) В бензине и воде сила Архимеда, действующая на цилиндр, одинакова.
2) Цилиндр не тонет в глицерине.
3) На цилиндр, погруженный в бромоформ, действует сила Архимеда 200мН.
4) Цилиндр плавает во всех жидкостях, указанных в таблице.
5) При плавании цилиндра в глицирине и бромоформе сила Архимеда, действующая на него, одинакова.
1) В бензине и в спирте цилиндр погружен на одинаковый объем. В таком случае сила Архимеда равна \[F_A=\rho gV_\text,\] где \(\rho\) – плотность жидкости, в которую погружено тело.
Но плотность спирта больше плотности бензина, а значит и сила Архимеда, действущая на цилиндр в спирте, больше силы Архимеда, действующей на цилиндр в бензине.
Утверждение 1 – \(\color>\)
2) Цилиндр тонет при плотности меньше, чем 1 г/см \(^3\) , у глицирина плотность 1,26 г/см \(^3\) , значит, цилиндр плавает.
Утверждение 2 – \(\color>\)
3) У бромоформа плотность больше 1 г/см \(^3\) , а значит сила Архимеда уравновешивает силу тяжести.
По графику видим, что цилиндр начинает плавать при плотности жидкости 1г/см \(^3\) , а значит именно такова плотность материала, из которого он сделан. Откуда сила Архимеда, действующая на цилиндр \[F_A=mg=1\text< г/см$^3$>\cdot 10\text< см$^3$>\cdot 10\text< Н/кг>=100\text< мН>\] Утверждение 3 – \(\color>\)
4) Нет, при плотности меньше 1 г/см3 цилиндр не плавает.
Утверждение 4 – \(\color>\)
5) У глицирина и бромоформа плотность больше 1 г/см \(^3\) , а значит сила Архимеда уравновешивает силу тяжести и силы Архимеда одинаковы.
Подготовка к ЕГЭ по физике задание №5 с ответами
1. В инерциальной системе отсчёта вдоль оси Ох движется тело массой 20 кг. На рисунке приведён график зависимости проекции скорости V этого тела от времени t. Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
1) Модуль ускорения тела в промежутке времени от 60 до 80 с в 3 раза больше модуля ускорения тела в промежутке времени от 80 до 100 с.
2) В промежутке времени от 80 до 100 с тело переместилось на 30 м.
3) В момент времени 90 с модуль равнодействующей сил, действующих на тело, равна 1,5 Н.
4) В промежутке времени от 60 до 80 с импульс тела увеличился на 40 кг • м/с.
5) Кинетическая энергия тела в промежутке времени от 10 до 20 с увеличилась в 4 раза.
2. На рисунке приведены графики зависимости координаты от времени для двух тел: A и B, движущихся по прямой, вдоль которой направлена ось Ох. Выберите два верных утверждения о характере движения тел.
1) Тело А движется равноускоренно, а тело В — равнозамедленно.
2) Скорость тела А в момент времени t = 5 с равна 20 м/с.
3) Тело В меняет направление движения в момент времени t = 5 с.
4) Проекция ускорения тела В на ось Ох положительна.
5) Интервал между моментами прохождения телом В начала координат составляет 6 с.
3. Автомобиль массой 2 т проезжает верхнюю точку выпуклого моста, радиус кривизны которого равен 40 м, со скоростью 36 км/ч. Из приведённого ниже списка выберите два правильных утверждения, характеризующие движение автомобиля в этот момент времени, и укажите их номера.
1) Равнодействующая сила, действующая на автомобиль, направлена вертикально вниз и перпендикулярна скорости автомобиля.
2) Сила, с которой мост действует на автомобиль, меньше 20 000 Н и направлена вертикально вверх.
3) Вес автомобиля равен 25 000 Н.
4) Центростремительное ускорение автомобиля равно 32,4 м/с2.
5) Вес автомобиля направлен вертикально вверх.
4. Математический маятник с частотой колебаний 0,5 Гц отклонили на небольшой угол от положения равновесия в положение 1 и отпустили из состояния покоя (см. рисунок). Сопротивлением воздуха пренебречь. Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
1) При движении из положения 1 в 2 модуль центростремительного ускорения груза маятника увеличивается.
2) Потенциальная энергия маятника в первый раз достигнет своего максимума через 1 с после начала движения.
3) Через 4 с маятник первый раз вернётся в положение 1.
4) Кинетическая энергия маятника в первый раз достигнет своего максимума через 1 с после начала движения.
5) При движении из положения 1 в 2 полная механическая энергия маятника увеличивается.
5. На рисунке приведены графики зависимости от времени t проекций скоростей Vx на ось Ох двух тел, движущихся по этой оси. Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
1) Проекция на ось Ох ускорения тела 1 меньше проекции на ось Ох ускорения тела 2.
2) Проекция на ось Ох ускорения тела 1 равна 0,3 м/с2.
3) Тело 2 в момент времени 15 секунд находилось в начале отсчёта.
4) Первые 15 секунд тела двигались в противоположные стороны.
5) Проекция на ось Ох ускорения тела 2 равна 0,1 м/с2.
6. На полу лифта расположены два одинаковых металлических бака, в которых доверху налит керосин (см. рисунок).
Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
1) Давление керосина на дно первого бака в 2 раза больше, чем на дно второго.
2) Оба бака давят на пол лифта с одинаковой силой.
3) Силы давления керосина на дно первого и второго баков одинаковы.
4) Оба бака оказывают на пол лифта одинаковое давление.
5) Если лифт начнёт движение вниз с ускорением 3 м/с2, давление керосина на дно баков увеличится на 30 %.
7. Бусинка может свободно скользить по неподвижной горизонтальной спице. На графике изображена зависимость её координаты от времени. Выберите два утверждения, которые можно сделать на основании графика.
1) Скорость бусинки на участке 1 постоянна, а на участке 2 равна нулю.
2) Проекция ускорения бусинки на участке 1 положительна, а на участке 2 — отрицательна.
3) Участок 1 соответствует равномерному движению бусинки, а на участке 2 бусинка неподвижна.
4) Участок 1 соответствует равноускоренному движению бусинки, а участок 2 — равномерному.
5) Проекция ускорения бусинки на участке 1 отрицательна, а на участке 2 — положительна.
8. В лабораторных опытах по изучению закона Гука две пружины с различной жёсткостью прикрепили к штативу, поочерёдно подвешивали к ним грузы разной массы и измеряли линейкой удлинение пружин. Результаты опытов с учётом погрешностей представлены в таблице.
Читайте также:
