Между пластинами 1 и 3 плоского конденсатора помещена тонкая металлическая пластина

Обновлено: 23.01.2025

Мы ВКонтакте

JS: 2.15.22
CSS: 4.9.20
jQuery: 3.6.1

DataForLocalStorage: 2022-09-21 11:45:59-standard

Bootstrap
Font Awesome

Коцюрбенко Алексей Владимирович (Старший модератор)

Физика

Образование Технические науки Решение задач

Консультации и решение задач по физике.

Здравствуйте! У меня возникли сложности с такими вопросами:

1.. В плоский конденсатор, расстояние между пластинами которого d = 2 см, вводится стеклянная пластинка (ξ = 6) толщиной d1 = 1.5 см. Во сколько раз при этом изменилась электроёмкость конденсатора? На какое расстояние Δd нужно раздвинуть его обкладки, чтобы получить начальную электроёмкость?

2.Между двумя металлическими пластинами, находящимися на расстоянии d = 5 см друг от друга создана разность потенциалов Δφ= 200 В. Затем в пространство между пластинами вводится стеклянная пластинка, относительная диэлектрическая проницаемость которой ξ = 7, а толщина равна d. Найти поверхностную плотность σ_p связанных зарядов, возникших на поверхности пластинки.

Здравствуйте, Голицина Дарья Сергеевна!

Предлагаю Вам следующее решение первой задачи.

Воспользуемся формулой электроёмкости плоского конденсатора, заполненного двумя слоями диэлектриком толщиной d и d₁ каждый с диэлектрическими проницаемостями ε и ε₁. В нашем случае ε = 1, ε₁ = 6, d₁ = 1,5 см.

Тогда получим следующие результаты:
1) электроёмкость конденсатора до ввода стеклянной пластинки (d = 2 см)
C₁ = ε₀εS/d;
2) электроёмкость конденсатора после ввода стеклянной пластинки (d' = d - d₁ = 2 - 1,5 = 0,5 (см))
C₂ = ε₀S/(d'/ε + d₁/ε₁);
3) электроёмкость конденсатора с введённой стеклянной пластинкой и раздвинутыми обкладками
C₃ = ε₀S/((d' + Δd)/ε + d₁/ε₁).

Найдём отношение электроёмкостей C₂ и C₁:
C₂/C₁ = ε₀S/(d'/ε + d₁/ε₁) : ε₀εS/d = d/ε 1/(d'/ε + d₁/ε₁) = dεε₁/(ε(ε₁d' + εd₁)) = dε₁/(ε₁d' + εd₁),
или
C₂/C₁ = 2 6/(6 0,5 + 1 1,5) = 12/4,5,
т. е. после ввода стеклянной пластинки электроёмкость конденсатора увеличилась в 12/4,5 ≈ 2,67 раза.

Для определения величины Δd, на которую необходимо раздвинуть обкладки конденсатора, чтобы его электроёмкость стала прежней, приравняем электроёмкости C₁ и C₃. Получим
ε₀εS/d = ε₀S/((d' + Δd)/ε + d₁/ε₁),
ε/d = 1/((d' + Δd)/ε + d₁/ε₁),
ε((d' + Δd)/ε + d₁/ε₁) = d,
ε(ε₁(d' + Δd) + εd₁) = εε₁d,
ε₁(d' + Δd) + εd₁ = ε₁d,
(d' + Δd) = (ε₁d - εd₁)/ε₁,
Δd = (ε₁d - εd₁)/ε₁ - d',
или
Δd = (6 2 - 1 1,5)/6 - 0,5 = 1.25 (см),
т. е. для получения начальной электроёмкости обкладки конденсатора необходимо раздвинуть на 1,25 см.

Между пластинами 1 и 3 плоского конденсатора помещена тонкая металлическая пластина

§ 1.28. Примеры решения задач

Электрическая емкость — последняя тема главы «Электростатика». При решении задач на эту тему могут потребоваться все сведения, полученные при изучении электростатики: сохранение электрического заряда, понятия напряженности поля и потенциала, поведение проводников в электростатическом поле, изменение напряженности поля в диэлектриках, закон сохранения энергии применительно к электростатическим явлениям. Только при хорошем усвоении всех основных понятий электростатики решение задач на электрическую емкость не вызовет особых затруднений.

Основными формулами при решении задач на емкость являются следующие: формула (1.24.2) — определение емкости, формула (1.24.3) — емкость уединенного шара, выражения для емкости плоского конденсатора (1.25.3) и сферического конденсатора (1.25.7), а также формулы для определения емкости батареи конденсаторов при последовательном и параллельном их соединении (1.26.4) и (1.26.2).

Надо знать еще формулы (1.27.3) и (1.27.9) для энергии заряженного конденсатора и заряженного уединенного тела.

Задача 1

Два одинаковых металлических шарика радиусом г расположены в вакууме на расстоянии d друг от друга, причем d >> r. Шарики заряжены одинаковыми по модулю и противоположными по знаку зарядами. Какова электрическая емкость системы, образованной шариками?

Решение. Искомая емкость равна отношению заряда q одного из шариков к разности потенциалов между ними:

Найдем U. Потенциал φ₁ первого шарика, несущего заряд +q, складывается из его собственного потенциала : (см. задачу 16 § 1.23).

Аналогично потенциал второго шарика

Отсюда разность потенциалов

Поскольку d >> r, то с большой степенью точности можно считать, что

Задача 2

Найдите емкость С конденсатора, площадь пластин которого S и расстояние между ними l, если в конденсатор вставлена металлическая пластина толщиной d, параллельная его обкладкам (рис. 1.107).

Решение. Конденсатор со вставленной в него пластиной можно рассматривать как два последовательно соединенных конденсатора. Емкость первого из них . При последовательном соединении электрическая емкость батареи определяется уравнением:

Емкость не зависит от положения пластины. При очень тонкой пластине (d ⇒ 0) емкость конденсатора не зависит от наличия пластины.

Задача 3

В плоский конденсатор с расстоянием d между обкладками вводится диэлектрическая пластина, толщина которой d₁ < d.

Определите емкость конденсатора с диэлектрической пластиной. Диэлектрическая проницаемость материала пластины ε. Площадь пластины и каждой обкладки конденсатора S.

Решение. Если в плоский конденсатор внести очень тонкую проводящую пластину, параллельную обкладкам, то на ее поверхностях появятся заряды противоположных знаков, равные по модулю. При этом емкость конденсатора не изменяется (см. задачу 2). Поэтому можно считать, что на поверхностях диэлектрической пластины нанесены тонкие проводящие слои. В этом случае образуются три последовательно соединенных конденсатора с емкостями

где d₂ и d₃ — расстояния между поверхностями диэлектрической пластины и обкладками, причем d₂ + d₂ = d - d₁ (рис. 1.108).

Емкость С батареи из трех конденсаторов определяется из формулы

Задача 4

Ha рисунке 1.109 изображена батарея конденсаторов. Их емкости равны С₁ = C, C₂ = 2С, C₃ = ЗС, С₄ = 6С. Изменится ли емкость батареи, если между точками А и В включить конденсатор с емкостью C₅ = 8С?

Решение. Обозначим потенциалы на зажимах батареи φ₁ и φ₂, а в точках А и В соответственно φ₃ и φ₄.

Так как конденсаторы С1 и СЗ соединены последовательно, то их заряды одинаковы, т.е.

Разделив почленно равенство (1.28.1) на равенство (1.28.2) и учитывая, что, согласно условию задачи,

Отсюда найдем, что φ₃ = φ₄. т. е. точки А и В имеют одинаковые потенциалы. Поэтому если включить какой-либо конденсатор между точками А и В (рис. 1.110), то он не зарядится и, следовательно, не повлияет на емкость системы.

Схема, подобная схеме, изображенной на рисунке 1.110, называется мостовой. Конденсаторы С1 и С2, СЗ и С4 называются плечами моста. Обратите внимание, что если емкости плеч моста пропорциональны , то точки А и В имеют одинаковые потенциалы. Конденсатор С5 не заряжается, и его из схемы можно удалить (см. рис. 1.109).

Задача 5

Найдите емкость батареи конденсаторов, изображенной на рисунке 1.111. Емкость каждого конденсатора равна С.

Решение. Данная схема соединения конденсаторов эквивалентна схеме, изображенной на рисунке 1.112. В этом можно убедиться, проверив, что каждый из конденсаторов соединен с источником и с другими конденсаторами точно так же, как в исходной схеме.

Вследствие равенства емкостей всех конденсаторов разность потенциалов между точками А и В равна нулю. Поэтому конденсатор 4 можно исключить (см. задачу 4). В результате получится схема, изображенная на рисунке 1.113. Она состоит из трех параллельных ветвей, две из которых содержат по два последовательно включенных конденсатора.

Общая емкость системы

Задача 6

Два маленьких шарика радиусом г несут заряды q₁ и q₂, различные по модулю, но одинаковые по знаку. Шарики первоначально находятся на расстоянии l друг от друга. Один из шариков закреплен. Второй шарик, удаляясь под действием электростатических сил, приобретает максимальную кинетическую энергию W_k1. Если перед началом движения второго шарика оба шарика на некоторое время были соединены проводником, то второй шарик, удаляясь, приобретает максимальную кинетическую энергию W_k2 > W_k1. Определите количество теплоты, выделившееся в проводнике при соединении шариков, и выясните, за счет какой энергии выделяется эта теплота и увеличивается кинетическая энергия второго шарика.

Решение. Согласно закрну сохранения энергии в первом случае

где W_k01 и W_p01 + W_0c — начальные, a W_k1 и W_p1 + W_1c — конечные значения кинетической и потенциальной энергий системы двух шариков. Причем W_p01 и W_1c, — потенциальные энергии взаимодействия шариков, а W_0c и W_1c — их суммарные собственные энергии, одинаковые по модулю. Считая потенциальную энергию взаимодействия при бесконечно большом расстоянии между шариками равной нулю и учитывая, что W_k01 = 0, получим:

После соединения проводником заряды шариков становят-ся одинаковыми и равными

Нетрудно видеть, что действительно W_k2 > W_k1. Кроме того, в проводнике выделяется количество теплоты Q. Однако, разумеется, полная энергия должна сохраняться. Увеличение кинетической энергии и выделение теплоты во втором случае происходит за счет уменьшения собственной потенциальной энергии заряженных шариков при их соединении.

С учетом собственной энергии шариков конечную энергию в первом случае можно представить в виде

— собственная энергия шариков. Конечную энергию во втором случае запишем так:

Количество выделенной теплоты равно:

Упражнение 4

1. Пластины заряженного конденсатора попеременно заземляются. Будет ли при этом конденсатор разряжаться?

2. Плоский конденсатор, расстояние между обкладками которого d₁ = 10 мм, зарядили до разности потенциалов U₁ = 100 В, а затем отключили от сети. Определите разность потенциалов U₂ между обкладками конденсатора, если их раздвинули до расстояния d₂ = 20 мм.

3. Определите емкость конденсатора, площадь пластин которого равна S, а расстояние между пластинами d, если пластины погружены вертикально в жидкий диэлектрик до середины. Диэлектрическая проницаемость диэлектрика равна е.

4. В конденсатор емкостью C₀ внесли диэлектрическую пластинку с диэлектрической проницаемостью ε = 2. Пластинку расположили так, как указано на рисунке 1.114. Определите, во сколько раз изменилась емкость конденсатора при внесении в него пластинки. Площадь пластинки в 2 раза меньше площади обкладки конденсатора, а ее толщина в 2 раза меньше расстояния между обкладками.

5. Плоский конденсатор, пространство между пластинами которого заполнено керосином (ε = 2), расположен вертикально, заряжен и отключен от источника напряжения. Напряженность электрического поля при этом в керосине Е = 20 кВ/см. Из-за дефекта в корпусе конденсатора керосин начинает вытекать, а его место занимает воздух. Предельная напряженность электрического поля в воздухе, при которой наступает электрический пробой (разряд), Е_пр = 30 кВ/см. Какая доля δ керосина вытечет из конденсатора к моменту пробоя конденсатора?

6. Оцените приближенно электрическую емкость тела человека.

7. Найдите емкость металлического шара радиусом r, окруженного прилегающим концентрическим слоем диэлектрика с внешним радиусом R и диэлектрической проницаемостью ε.

8. К пластинам плоского конденсатора, находящимся на расстоянии d = 1 см друг от друга, приложена разность потенциалов U = 300 В. В пространство между пластинами помещается плоскопараллельная пластина из стекла толщиной d₁ = 0,3 см и плоскопараллельная пластина из парафина толщиной d₂ = 0,7 см. Найдите напряжения между поверхностями стеклянной и парафиновой пластин. Диэлектрические проницаемости стекла и парафина соответственно равны ε₁ = б и ε₂ = 2,6.

9. Определите емкость конденсатора с трехслойным диэлектриком, диэлектрические проницаемости слоев равны ε₁, ε₂, ε₁ (рис. 1.115). Толщина каждого диэлектрика (слоя) равна d. Площадь пластин S.

10. Четыре одинаковые металлические пластины расположены в воздухе на равных расстояниях d друг от друга (d мало по сравнению с размерами пластин). Площадь каждой из пластин равна S. Пластина 1 соединена проводником с пластиной 3, а от пластин 2 и 4 сделаны выводы (рис. 1.116). Определите емкость С такого конденсатора.

11. Определите емкость С батареи конденсаторов, схематически изображенной на рисунке 1.117. У каждого конденсатора указано значение его емкости, выраженное в микрофарадах.

12. Из проволоки сделан куб, в каждое ребро которого включено по одному конденсатору емкостью С (рис. 1.118). Найдите емкость получившейся батареи конденсаторов, если она включается в цепь проводниками, присоединенными к вершинам А и В куба.

13. Имеется N точек в пространстве. Между каждой парой точек включен конденсатор емкостью С. Найдите емкость образовавшейся батареи конденсаторов, если она включается в цепь выводами, присоединенными к двум произвольным точкам.

14. Плоский конденсатор емкостью С = 15 пФ зарядили до разности потенциалов U = 100 В, затем отключили от источника и погрузили полностью в жидкий диэлектрик (ε = 1,5). Определите изменение энергии конденсатора ΔW_p.

15. Три конденсатора емкостью С = 1 мкФ каждый соединены последовательно. Конденсаторы зарядили и отключили от источника. Заряд этой батареи q = 10 -4 Кл. Затем пространство между обкладками одного из конденсаторов заполнили диэлектриком с диэлектрической проницаемостью ε = 2. Найдите энергию, запасенную в электрическом поле этих конденсаторов, и напряжение на зажимах батареи после заполнения диэлектриком одного из конденсаторов.

16. Энергия заряженного плоского конденсатора, заполненного диэлектриком, равна W_p = 2 • 10 -5 Дж. После отключения конденсатора от источника напряжения диэлектрик из конденсатора вынули, совершив при этом работу А = 7 • 10 -5 Дж. Найдите диэлектрическую проницаемость диэлектрика.

17. Сделаем в пластинах плоского конденсатора два малых отверстия — одно напротив другого. Пусть через одно из отверстий в заряженный конденсатор влетает с небольшой начальной скоростью частица так, чтобы электрическое поле конденсатора ускоряло ее (рис. 1.119).

Пролетев через конденсатор, частица вылетает из другого отверстия, приобретая дополнительную энергию ΔW_p = qU, где q — заряд частицы, а U — разность потенциалов на пластинах конденсатора. Теперь с помощью магнитного поля направление движения частицы изменяется таким образом, чтобы она снова влетела через первое отверстие в конденсатор (см. рис. 1.119). (В главе 4 вы узнаете, что сила, действующая со стороны магнитного поля на движущуюся заряженную частицу, не совершает работы.) При повторном пролете через конденсатор частица вновь приобретает дополнительную энергию ΔW_p, в следующем цикле — еще ΔW_p и т. д. Получается циклический ускоритель, который не нуждается в источнике энергии! Где ошибка в приведенных рассуждениях?

18. Два конденсатора емкостью С₁ и C₂ заряжены до разности потенциалов U₁ и U₂ (U₁ ≠ U₂). Докажите, что при параллельном соединении этих конденсаторов их общая энергия уменьшается. Объясните, почему происходит уменьшение энергии.

19. Две прямоугольные пластины длиной l и площадью S расположены параллельно друг другу на расстоянии d (плоский конденсатор). Пластины заряжены до разности потенциалов U. В пространство между пластинами втягивается диэлектрик с диэлектрической проницаемостью ε. Толщина диэлектрика равна d, его ширина равна ширине пластин, а длина больше l (рис. 1.120). Трение отсутствует. Найдите зависимость силы, действующей на диэлектрик со стороны поля, от расстояния х.

20. Решите задачу 19 при условии, что разность потенциалов между пластинами поддерживается постоянной и равной U.

Мы потратили довольно много времени на изучение электричества, а рассмотрели лишь простейший частный случай неподвижных заряженных тел — электростатику. Может быть, не стоило уделять электростатике такое больпюе внимание? Нет, стоило! Мы ввели важнейшие понятия, используемые во всей электродинамике: «электрический заряд», «электрическое поле», «потенциал» и «разность потенциалов», «электрическая емкость», «энергия электрического поля». На простом частном случае выяснить суть этих фундаментальных понятий не так трудно, как в общем случае движущихся зарядов.

Теперь перейдем к изучению электромагнитных процессов, наблюдаемых при движении заряженных частиц.

Жидкевич В.И. Электрическое поле плоскости

Жидкевич В. И. Электрическое поле плоскости // Фізіка: праблемы выкладання. — 2009. — № 6. — С. 19—23.

Задачи по электростатике можно разделить на две группы: задачи о точечных зарядах и задачи о заряженных телах, размеры которых нельзя не учитывать [1—5].

Решение задач по расчёту электрических полей и взаимодействий точечных зарядов основано на применении закона Кулона и не вызывает особых затруднений. Более сложным является определение напряжённости поля и взаимодействия заряженных тел конечных размеров: сферы, цилиндра, плоскости. При вычислении напряжённости электростатических полей различной конфигурации следует подчеркнуть важность принципа суперпозиции и использовать его при рассмотрении полей, созданных не только точечными зарядами, но и зарядами, распределёнными по поверхности и объёму. При рассмотрении действия поля на заряд формула F=qE в общем случае справедлива для точечных заряженных тел и только в однородном поле применима для тел любых размеров и формы, несущих заряд q.

Электрическое поле конденсатора получается в результате наложения двух полей, созданных каждой пластиной.

В плоском конденсаторе можно рассматривать одну пластину как тело с зарядом q₁ помещённое в электрическое поле напряжённостью Е₂, созданное другой пластиной.

Рассмотрим несколько задач.

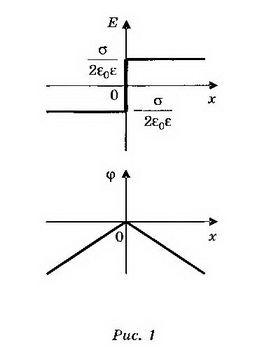
1. Бесконечная плоскость заряжена с поверхностной плотностью σ >0. Найдите напряжённость поля Е и потенциал ϕ по обе стороны плоскости, считая потенциал плоскости равным нулю. Постройте графики зависимостей Е(х), ϕ (х). Ось х перпендикулярна плоскости, точка х=0 лежит на плоскости.

Решение. Электрическое поле бесконечной плоскости является однородным и симметричным относительно плоскости. Его напряжённость где х — расстояние между точками, измеренное вдоль силовой линии. Тогда ϕ ₂= ϕ ₁-Eх. При х ϕ (х) представлены на рисунке 1.

2. Две плоскопараллельные тонкие пластины, расположенные на малом расстоянии d друг от друга, равномерно заряжены зарядом поверхностной плотностью σ₁ и σ ₂. Найдите напряжённости поля в точках, лежащих между пластинами и с внешней стороны. Постройте график зависимости напряжённости Е(х) и потенциала ϕ (х), считая ϕ (0)=0. Рассмотрите случаи, когда: a) σ ₁=- σ ₂; б) σ₁ = σ ₂; в) σ ₁=3 σ ₂-

Решение. Так как расстояние между пластинами мало, то их можно рассматривать как бесконечные плоскости.

Напряжённость поля положительно заряженной плоскости равна

Согласно принципу суперпозиции поле в любой рассматриваемой точке будет создаваться каждым из зарядов в отдельности.

а) Поля двух плоскостей, заряженных равными и противоположными по знаку зарядами (плоский конденсатор), складываются в области между плоскостями и взаимно уничтожаются во внешних областях (рис. 2, а).

При хЕ= 0, ϕ =0; при 0 d Е= 0,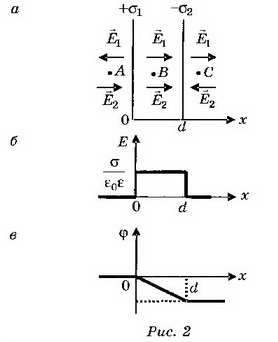

Если плоскости конечных размеров, то поле между плоскостями не будет строго однородным, а поле вне плоскостей не будет точно равно нулю.

б) Поля плоскостей, заряженных равными по величине и знаку зарядами ( σ₁ = σ₂ ), компенсируют друг друга в пространстве между плоскостями и складываются во внешних областях (рис. 3, а). При х<0 d

Воспользовавшись графиком Е(х) (рис. 3, б), построим качественно график зависимости ϕ (х) (рис. 3, в).

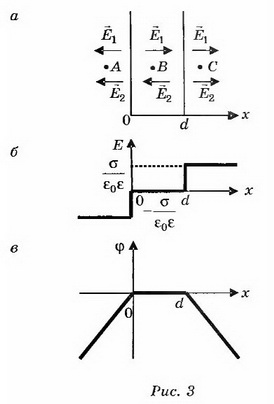
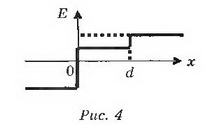
в) Если σ₁ = σ ₂, то, учитывая направления полей и выбирая направление направо за положительное, находим:

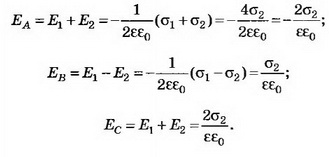
Зависимость напряжённости Е от расстояния показана на рисунке 4.

3. На одной из пластин плоского конденсатора ёмкостью С находится заряд q₁ =+3q, а на другой q₂ =+ q. Определите разность потенциалов между пластинами конденсатора.

Решение. 1-й способ. Пусть площадь пластины конденсатора S, а расстояние между ними d. Поле внутри конденсатора однородное, поэтому разность потенциалов (напряжение) на конденсаторе можно определить по формуле U=E*d, где Е — напряжённость поля внутри конденсатора.

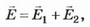
где Е₁, Е₂ — напряжённости поля, создаваемого пластинами конденсатора.

Тогда

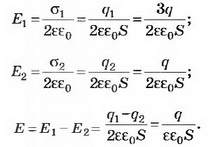
2-й способ. Добавим на каждую пластину заряд q и -q. Поля одинаковых зарядов пластин внутри конденсатора компенсируют друг друга. Добавленные заряды не изменили поле между пластинами, а значит, и разность потенциалов на конденсаторе. U= q/C .

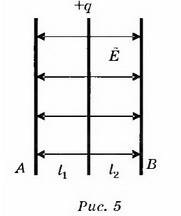
4. В пространство между обкладками незаряженного плоского конденсатора вносят тонкую металлическую пластину, имеющую заряд +q. Определите разность потенциалов между обкладками конденсатора.

Решение. Так как конденсатор не заряжен, то электрическое поле создаётся только пластиной, имеющей заряд q (рис. 5). Это поле однородное, симметричное относительно пластины, и его напряжённость ϕ . Тогда потенциалы обкладок А и В конденсатора будут равны ϕ- ϕ_А = ϕ El₁ ; ϕ_А = ϕ-El₁ ; ϕ- ϕ_B = ϕ-El₂ ; ϕ_B = ϕ-El₂ .

Разность потенциалов между обкладками конденсатора

5. В однородное электрическое поле напряжённостью Е₀ перпендикулярно силовым линиям помещают заряженную металлическую пластину с плотностью заряда на поверхности каждой стороны пластины σ (рис. 6). Определите напряжённость поля Е' внутри и снаружи пластины и поверхностную плотность зарядов σ₁ и σ₂ , которая возникнет на левой и правой сторонах пластины.

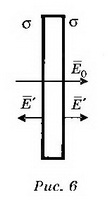
Решение. Поле внутри пластины равно нулю и является суперпозицией трёх полей: внешнего поля Е₀, поля, создаваемого зарядами левой стороны пластины, и поля, создаваемого зарядами правой стороны пластины. Следовательно, 1 и σ ₂ — поверхностная плотность заряда на левой и правой сторонах пластины, которая возникает после внесения пластины в поле Е₀. Суммарный заряд пластины не изменится, поэтому σ ₁ + σ₂ =2 σ , откуда σ₁ = σ- ε ₀ E ₀, σ₂ = σ + ε ₀ E ₀ . Поле снаружи пластины является суперпозицией поля Е₀ и поля заряженной пластины Е. Слева от пластины

6. В плоском воздушном конденсаторе напряжённость поля Е= 10 4 В/м. Расстояние между обкладками d= 2 см. Чему будет равна разность потенциалов, если между пластинами параллельно им поместить металлический лист толщиной d₀ =0,5 см (рис. 7)?

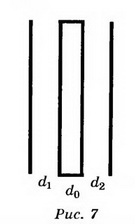
Решение. Поскольку электрическое поле между пластинами однородное, то U=Ed, U=200 В.

Если между пластинами пометить металлический лист, то получается система из двух последовательно соединённых конденсаторов с расстоянием между пластинами d₁ и d₂. Ёмкости этих конденсаторов Их общая ёмкость

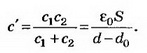
Так как конденсатор отключён от источника тока, то заряд конденсатора при внесении металлического листа не меняется: q'=CU=С'U₁; емкость конден сатора до внесения в него металлического листа. Получаем:

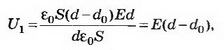
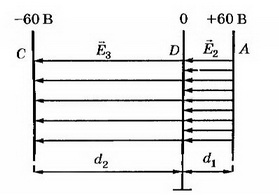
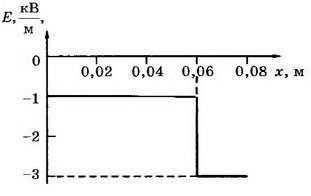
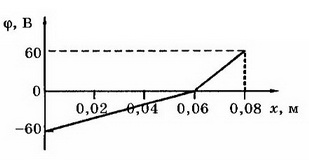
7. На пластинах А и С, расположенных параллельно на расстоянии d= 8 см друг от друга, поддерживаются потенциалы ϕ₁ = 60 В и ϕ₂ =- 60 В соответственно. Между ними поместили заземлённую пластину D на расстоянии d₁ = 2 см от пластины А. На сколько изменилась напряжённость поля на участках AD и CD? Постройте графики зависимостей ϕ (x) и Е(х).

Решение. Первоначальная напряжённость поля между пластинами А и С:

Напряжённость поля на участке AD: Е₂= ϕ₁/d₁ , Е₂ = 3 кВ/м, т. е. увеличилась на 1,5 кВ/м. Напряжённость поля на участке CD Е₃= ϕ₂/d₂ , т.е. уменьшилась на Е₃ = 0,5 кВ/м. Поскольку векторы г, Е₂, Е₃< 0 (рис. 8).

8. Точечный заряд q=5*10 -9 Кл находится на расстоянии 3 см от проводящей заземлённой стенки. Найдите поверхностную плотность заряда, индуцированного на стенке в точке А, ближайшей к заряду, и в точке В, находящейся на расстоянии 5 см от заряда.

Решение. В точках А, В, расположенных в непосредственной близости к поверхности проводника (рис. 9), поле создаётся точечным зарядом q и зарядом q', индуцированным на стенке: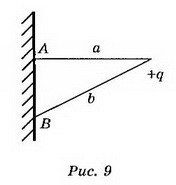

В точке А . Но поле внутри проводника равно нулю; следовательно,

В точке В величина нормальной составляющей напряжённости поля точечного заряда

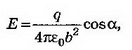
где b — расстояние от заряда до точки, cos α =a/b, Следовательно,

Список использованной литературы

1. Балаш, В. А. Задачи по физике и методы их решения / В. А. Балаш. — 4-е изд. — М. : Просвещение, 1983. — 432 с.

2. Бутиков, Е. И. Физика в примерах и задачах / Е. И. Бутиков, А. А. Быков, А. С. Кондратьев. — 3-е изд. — М. : Наука, 1989. — 462 с.

3. Зилъберман, Г. Е. Электричество и магнетизм / Г. Е. Зильберман. — М. : Наука, 1990. — 384 с.

4. Меледин, Г. В. Физика в задачах / Г. В. Меледин. — 2-е изд. — М. : Наука, 1990. — 270 с.

5. Сборник задач по физике / Л. П. Баканина [и др.]; под ред. С. М. Козела. — М. : Наука, 1990. — 347 с.

Читайте также: