Металлы по зонной теории
Если два различных металла привести в соприкосновение, то между ними возникает разность потенциалов, называемая контактной разностью потенциалов.Итальянский физик А. Вольта (1745 – 1827) установил, что если металлы А1, Zn, Sn, Pb, Sb, Bl, Hg, Fe, Cu, Ag, Au, Pt, Pb привести в контакт в указанной последовательности, то каждый предыдущий при соприкосновении с одним из следующих зарядится положительно. Этот ряд называется рядом Вольта.Контактная разность потенциалов для различных металлов составляет от десятых до целых вольт.
Вольтаэкспериментально установил два закона:
1. Контактная разность потенциалов зависит лишь от химического состава и температуры соприкасающихся металлов.
2. Контактная разность потенциалов последовательно соединенных различных проводников, находящихся при одинаковой температуре, не зависит от химического состава промежуточных проводников и равна контактной разности потенциалов, возникающей при непосредственном соединении крайних проводников.
Для объяснения возникновения контактной разности потенциалов воспользуемся представлениями зонной теории. Рассмотрим контакт двух металлов с различными работами выхода А1 и А2 , т.е. с различными положениями уровня Ферми (верхнего заполненного электронами энергетического уровня). Если А1 < А2 (этот случай изображен на рис. 26, а), то уровень Ферми располагается в металле 1 выше, чем в металле 2. Следовательно, при контакте металлов электроны с более высоких уровней металла 1 будут переходить на более низкие уровни металла 2, что приведет к тому, что металл 1 зарядится положительно, а металл 2 – отрицательно. Одновременно происходит относительное смещение энергетических уровней: в металле, заряжающемся положительно, все уровни смещаются вниз, а в металле, заряжающемся отрицательно, – вверх. Этот процесс будет происходить до тех пор, пока между соприкасающимися металлами не установится равновесие, которое, как доказывается в статистической физике, характеризуется; совпадением уровней Ферми в обоих металлах (рис. 26, 6).
Так как для соприкасающихся металлов уровни Ферми совпадают, а работы выхода А1и А2не изменяются (они являются константами металлов и не зависят от того, находятся металлы в контакте или нет), то потенциальная энергия электронов в точках, лежащих вне металлов в непосредственной близости к их поверхности (точки А и В на рис. 26, б), будет различной. Следовательно, между точками А и В устанавливается разность потенциалов, которая, как следует из рисунка, равна
Δφ' = (А2 – А1) / е. (246.1)

Разность потенциалов (246.1), обусловленная различием работ выхода контактирующих металлов, называется внешней контактной разностью потенциалов.Чаще говорят просто о контактной разности потенциалов, подразумевая под ней внешнюю.
Если уровни Ферми для двух контактирующих металлов не одинаковы, то между внутренними точками металлов наблюдается внутренняя контактная разность потенциалов,которая, как следует из рисунка, равна
Δφ'' =В квантовой теории доказывается, что причиной возникновения внутренней контактной разности потенциалов является различие концентраций электронов и контактирующих металлах. Δφ'' зависит от температуры Т контакта металлов (поскольку наблюдается зависимость EF от Т), обусловливая термоэлектрические явления. Как правило, Δφ'' φ'.
Если, например, привести в соприкосновение три разнородных проводника, имеющих одинаковую температуру, то разность потенциалов между концами разомкнутой цепи равна алгебраической сумме скачков потенциала во всех контактах. Она, как можно показать (предоставляем это сделать читателю), не зависит от природы промежуточных проводников (второй, закон вольта).
Внутренняя контактная разность потенциалов возникает в двойном электрическом слое, образующемся вприконтактной области, называемом контактным слоем.Толщина контактного слоя в металлах составляет примерно 10 –10 м, т. е. соизмерима с междоузельными расстояниями в решетке металла. Число электронов, участвующих и диффузии через контактный слой, составляет примерно 2 % от общего числа электронов, находящихся на поверхности металла. Столь незначительное изменение концентрации электронов в контактном слое, с одной стороны, и малая по сравнению с длиной свободного пробега электрона его толщина – с другой, не могут привести к заметному изменению проводимости контактного слоя по сравнению с остальной частыо металла. Следовательно, электрический ток через контакт двух металлов проходит так же легко, как и через сами металлы, т.е. контактный слой проводит электрический ток в обоих направлениях (1 → 2 и 2 → 1)одинаково и не дает эффекта выпрямления, который всегда связан с односторонней проводимостью.
Зонная теория твердых тел
Основываясь лишь на модели электронного газа невозможно объяснить тот факт, что одни вещества представляют собой проводники, вторые полупроводники, а третьи изоляторы. Стоит принимать во внимание взаимодействие между атомами и электронами. Предположим, что кристаллическая решетка металла или полупроводника сформирована как результат сближения атомов. Связь с атомными ядрами валентных электронов атомов металлов проявляет себя гораздо слабее, чем связь с подобными электронами полупроводников. При условии сближения атомов электроны приходят во взаимодействие. В результате валентные электроны разрывают свою связь с атомами металла, что делает их свободными, обладающими возможностью перемещаться по всему металлу.
В полупроводниках, по причине существенно более сильной связи электронов с ядрами атомов, для того, чтобы разорвать связь валентного электрона нужно сообщить ему так называемую энергию ионизации.
Для разных полупроводников величина энергии ионизации может колебаться от 0 , 1 до 2 э В , в то же время средняя кинетическая энергия теплового движения атома близка к 0 , 04 э В . Количество атомов, энергия которых выше или эквивалентна энергии ионизации, относительно невелико. Соответственно, свободных электронов в полупроводниках не много. С увеличением температуры, число атомов с энергией ионизации повышается, а это значит, что растет и электрическая проводимость полупроводника.
За процессом ионизации всегда идет сопровождение в виде обратного процесса, а именно рекомбинация. В условиях состояния равновесия среднее число актов ионизации эквивалентно количеству актов рекомбинации.
Понятие о зонной теории
Квантовая теория электропроводности твердых тел основывается на так называемой зонной теории твердых тел, которая заключается в изучении энергетического спектра электронов.
Данный спектр подразделяется на разделенные запрещенными промежутками зоны. В случае, если в верхней зоне, где определяется присутствие электронов, они не заполняют каждое из квантовых состояний (в пределах зоны может быть проведено перераспределение энергии и импульса), то данное вещество представляет собой проводник. Подобная зона носит название зоны проводимости, вещество — проводника электрического тока, тип проводимости такого вещества является электронным.
Если в зоне проводимости находится большое количество электронов и свободных квантовых состояний, то значение электропроводности велико. Электроны в условиях зоны проводимости при прохождении электрического тока определяются как носители заряда. Процесс движения подобных электронов может быть описан с помощью законов квантовой механики. Если проводить сравнение с общим количеством электронов, то число таких электронов может считаться малым.
Энергетические уровни
Энергетические уровни валентного электрона в одном изолированном атоме могут быть представлены таким образом, как это проиллюстрировано на рисунке 1 . Снизу вверх по вертикали на рисунке 1 откладываются: величины полной энергии электрона, а также отмечаются минимальная энергия электронов проводимости E c с наибольшим значением энергии связанных электронов E v . Вероятные значения энергий электронов заполняют собой некоторую область или же так называемую зону энергии W ≥ E c . Такая зона представляет собой зону проводимости. Энергии электронов связи формируют другую зону с W ≤ E v . Приведенная зона носит название зоны валентных электронов или, другими словами, валентной зоны. Данные зоны разделены энергетическим промежутком с шириной, определяемой с помощью следующего выражения: E g = E c − E v .
Такой энергетический промежуток представляет собой зону запрещенных энергий. В условиях отсутствующих примесных атомов, а также дефектов решетки, стационарные движения электронов с энергией внутри запрещенной зоны не представляются возможными.
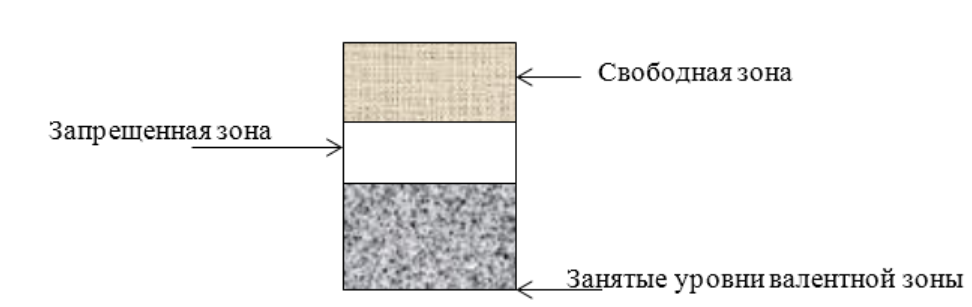
Процесс разрыва химической связи, который провоцирует возникновение электрона проводимости и положительной дырки, носит название электронного перехода.
Валентная зона — зона проводимости (смотрите рисунок 1 цифра 1 ).
Обратный процесс определяется как рекомбинация электрона проводимости и положительной дырки (электронный переход 2 , рисунок 1 ). В условиях существования атомов примеси вероятно возникновение дискретных разрешенных уровней энергии как ,например, уровень E d , проиллюстрированный на рисунке 1 . Данные уровни могут существовать не во всем объеме кристалла, а лишь в местах нахождения атомов примеси (такие уровни определяются как локальные). Каждый из локальных уровней производит энергию электрона, в случае его нахождения на примесном атоме. Локальные электронные уровни дают возможность дополнительных электронных переходов. Как пример, ионизация донора с образованием электрона проводимости проиллюстрирована на рисунке 1 в виде электронного перехода 3 . Роль обратного ему процесса захвата электрона на атом донора играет электронный переход 4 из зоны проводимости на незаполненный уровень донора.
Образование энергетических зон
Из решения задачи о движении электрона в поле периодического потенциала можно сделать вывод, что имеет место система зон разрешённых энергий (рисунок 2 ). Каждая из зон ограничивается снизу некоторой энергией W m i n или, другими словами, дном зоны, а сверху так называемым потолком зоны W m a x . Данные зоны разделены полосами запрещенных энергий. Ширина разрешенных зон в условиях увеличения энергии возрастает. Возможно перекрытие друг друга широкими зонами, такое явление провоцирует образование единой сложной зоны. Предположим, что существует N изолированных атомов, которые никоим образом не взаимодействуют. В каждом из таких атомов энергия электронов может претерпевать изменения только в виде скачка, таким образом, она характеризуется совокупностью резких, дискретных уровней энергии. В данной системе невзаимодействующих атомов роль каждого атомного энергетического уровня играет N совпадающих уровней энергии. Сократим расстояние между атомами до формирования кристаллической решетки. Атомы начинают взаимодействовать друг с другом, а уровни энергии изменяются. Ранее совпадающие N уровней энергии начинают разниться. Подобная система несовпадающих уровней энергии носит название разрешенной зоны энергий.
Выходит, что энергетические зоны возникают в качестве результата расщепления дискретных уровней энергии электрона в атомах, вызванного действием атомов решетки. Количество энергетических уровней в каждой из зон крайне большое (порядка числа атомов в кристалле), энергетические уровни расположены довольно близко. Таким образом, в некоторых случаях можно принять, что внутри зон энергия электрона претерпевает непрерывные изменения (как это происходит в классической теории). Однако тот факт, что количество уровней конечно, имеет принципиальное значение. Совокупность энергетических уровней, на которые расщепляется кратный уровень, представляет собой так называемую энергетическую зону или, другими словами, зону кристалла. Зона,возникающая как результат расщепления N -кратного вырожденного основного уровня, носит название основной зоны, все остальные зоны определяются как зоны возбуждения.
Энергетические зоны не могут быть отождествлены с пространственными зонами, областями пространства, в которых находится электрон.
В рамках зонной теории принимается тот факт, что электрон движется в постоянном электрическом поле, которое формируется ионами и остальными электронами. Ионы обладают сравнительно большими массами и считаются неподвижными. Электроны учитываются суммарно. Они определяются в виде отрицательно заряженной жидкости, которая заполняет пустующее пространство между ионами. В подобной модели роль электронов заключается в компенсации заряда ионов. Электрическое поле модели периодично в пространстве, место периодов занимают пространственные периоды решетки. Задание сводится к задаче о движении одного электрона в постоянном периодическом поле. Решение данной задачи в квантовой механике приводит к зонной структуре энергетических уровней.
Дайте описание зонных структур металлов, диэлектриков и полупроводников.
Решение
Электрические свойства тел зависимы от ширины запрещенной энергетической зоны и различий в заполнении разрешенных зон. Существование в разрешенной зоне свободных энергетических уровней является необходимым условием возникновения проводимости. На данный уровень поле сторонних сил может перенести электрон. Зону, которая является пустой или же заполнена лишь частично определяется как зона проводимости. В свою очередь, зона, заполненная электронами полностью, носит название валентной. Металлы, диэлектрики и полупроводники отличаются в области степени заполнения валентной зоны электронами, а также шириной запретной зоны. У металлов зона проводимости является частично заполненной и обладает свободными верхними уровнями. При условии T = 0 валентные электроны попарно заполняют нижние уровни валентной зоны. Локализованным на верхних уровнях электронам для того, чтобы перевести их на более высокие уровни достаточно подвести энергию 10 - 23 - 10 - 22 э В . У диэлектриков первая, являющаяся незаполненной зона, отделена от целиком заполненной нижней зоны с помощью широкой запрещенной зоны. Чтобы перевести электрон в свободную зону необходимо сообщить энергию большую или же эквивалентную ширине запретной зоны. Ширина запрещенной зоны диэлектриков является равной нескольким электрон вольтам. Тепловое движение не имеет возможности перевести в свободную зону большое количество электронов. У кристаллических полупроводников ширина запрещенной зоны между полностью заполненной валентной зоной и первой незаполненной зоной довольно мала. Если ширина запретной зоны эквивалентна нескольким десятым э В , энергии теплового движения хватает для того, чтобы перевести электроны в свободную зону проводимости. При этом вероятен переход электрона внутри валентной зоны на освободившиеся уровни.
Перечислите основные предположения зонной теории.
В качестве основных предположений зонной теории можно привести следующие:
Особенности зонной структуры диэлектриков, полупроводников и металлов
Зонная теория - это квантовая механическая теория, которая рассматривает движение электронов в твердом теле.
Зонная теория твердого тела
Согласно теории, свободные электроны могут обладать любой энергией. Электроны в атомах твердого тела могут иметь только определенные дискретные значения энергии. Другими словами, спектр энергии электронов в атомах состоит из разрешенных и запрещенных энергетических зон.
Положения зонной теории
Итак, согласно постулатам Бора, электрон в отдельном атоме может находится на одной из нескольких энергетических орбиталей. Иначе говоря, иметь лишь определенные дискретные значения энергии. Когда атомы образуют молекулу, количество орбиталей расщепляется пропорционально числу атомов в молекуле.
При увеличении количества молекул до макроскопического тела количество орбиталей становится очень большим, а разница между соответствующими им энергиям - очень маленькой. Орбитали сливаются, образуя энергетические зоны.
Валентная зона - в диэлектриках и полупроводниках наивысшая энергетическая зона, которая заполнена полностью при температуре 0 К. Зона проводимости - следующая за валентной зона. В металлах зоной проводимости называется наивысшая разрешённая зона, в которой находятся электроны при температуре 0 К.
Зонная теория объясняет различие в электрических свойствах материалов: проводников, полупроводников, диэлектриков. Можно выделить следующие причины различий:
- Ширина запрещенных энергетических зон
- Разница в заполнении разрешенных энергетических зон электронами.
Зонная структура диэлектриков
Вещество является диэлектриком, когда валентная зона заполнена полностью, в высших зонах нет электронов, также отсутствует перекрытие зон. Такое вещество не проводит ток. Ширина между зонами у диэлектриков условно составляет более 2 электронвольт.
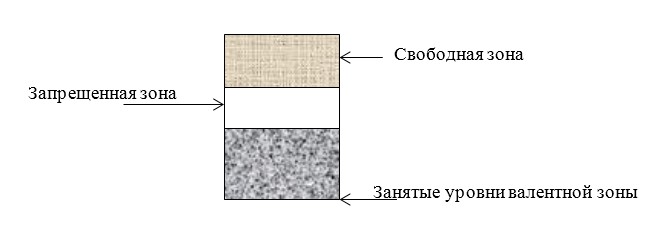
Зонная структура полупроводников
Вещество является полупроводником, если валентная зона разделена с соседними зонами узкой (менее 2 электронвольт) запрещающей зоной. Отметим, что такое вещество при температуре, близкой к абсолютному нулю, является диэлектриков. Однако при росте температуры электроны из верхней занятой зоны перескакивают в вакантную зону проводимости, и вещество становится электропроводным. Проводимость растет вместе с температурой и концентрацией электронов в зоне проводимости. Соответственно, в заполненной зоне, из которой электроны переходят в зону проводимости, растет концентрация дырок.
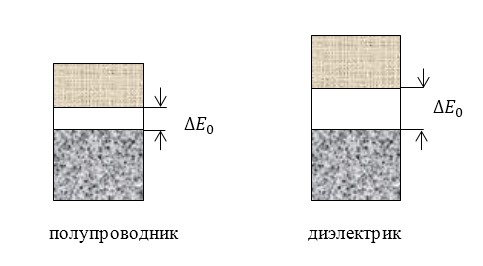
Разделение веществ на полупроводники и диэлектрики весьма условно. Вещества с шириной запрещённой зоны более 3—4 эВ и менее 4—5 эВ совмещают свойства диэлектриков и полупроводников.
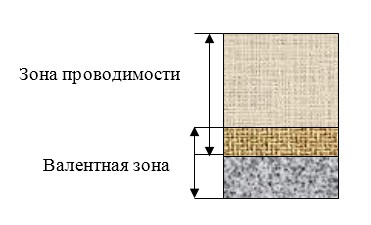
Зонная структура проводников (металлов)
В металлах валентная зона занята не полностью, и при воздействия на проводник разности потенциалов электроны могут свободно перемещаться из точек с меньшим потенциалом в точку с большим потенциалом.
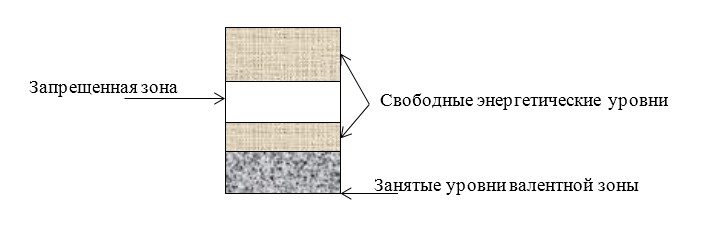
Также в проводниках зона проводимости пересекается с валентной зоной. Получившаяся зона пересечения заполнена не полностью.
Почему проводимость металлов не растет с увеличением валентности?
Валентность - это способность атома вещества образовать определенное число химических связей. Проще говоря, способность "прикрепить" к себе другой атом.
Однако электропроводность зависит не от количества валентных электронов на один атом, а от числа электронов в валентной зоне, для которых существуют свободные энергетические уровни. Так, у двухвалентных металлов число электронов, которые могут перейти под действием внешнего поля в свободное состояние меньше, чем у одновалентных. Таким образом, электропроводность двухвалентных металлов меньше, чем одновалентных.
Классическая электронная теория проводимости Друде-Лоренца
Теория Друде была разработана в 1900 году, через три года после открытия электрона. Затем теория была доработана Лоренцом, и сейчас она является классической и актуальной теорией проводимости металлов.
Электронная теория Друде-Лоренца
Согласно теории, носителями тока в металлах являются свободные электроны.
Друде предположил, что электроны в металле подчиняются и могут быть описаны уравнениями молекулярно-кинетической теории. Другими словами, свободные электроны в металле подчиняются законам МКТ и образуют "электронный газ".
Двигаясь в металле, электроны соударяются между собой и с кристаллической решеткой (это и есть проявление электрического сопротивления проводника). Между соударениями электроны, по аналогии с длиной свободного пробега молекул идеального газа, успевают преодолеть средний путь λ .
Без действия электрического поля, ускоряющего электроны, кристаллическая решетка и электронный газ стремятся к состоянию теплового равновесия.
Приведем основные положения теории Друде:
- Взаимодействие электрона с другими электронами и ионами не учитывается между столкновениями.
- Столкновения являются мгновенными событиями, внезапно меняющими скорость электрона.
- Вероятность для электрона испытать столкновение за единицу времени равна 1 τ .
- Состояние термодинамического равновесия достигается благодаря столкновениям.
Несмотря на множество допущений, теория Друде-Лорецна хорошо объясняет эффект Холла, явление удельной проводимости и теплопроводность металлов. Именно поэтому она актуальна по сей день, хотя ответы на многие вопросы (например, почему в металле существуют свободные ионы и электроны) смогла дать только квантовая теория твердого тела.
В рамках теории Друде объясняется сопротивление металлов. Оно обусловлено соударениями электронов с узлами кристаллической решетки.
Выделение тепла, согласно закону Джоуля-Ленца, также происходит по причине соударения электронов с ионами решетки.
Теплопередача в металлах также осуществляется электронами, а не кристаллической решеткой.
Терия Друде не объясняет многих явлений, как например сверхпроводимость, и не применима в сильных магнитных полях, в слабых магнитных полях может терять применимость из-за квантовых явлений.
Среднюю скорость электронов можно вычислить по формуле для идеального газа:
Здесь k - постоянная Больцмана, T - температура металла, m - масса электрона.
При включении внешнего электрического поля, на хаотичное движение частиц "электронного газа" накладывается упорядоченное движение электронов под действием сил поля, когда электроны начинают упорядоченно двигаться со средней скоростью u . Величину этой скорости можно оценить из соотношения:
где j - плотность тока, n - концентрация свободных электронов, q - заряд электрона.
При больших плотностях тока рассчеты дают следующий результат: средняя скорость хаотичного движения электронов во много раз ( ≈ 10 8 ) больше скорости упорядоченного движения под действием поля. При вычислении суммарной скорости полагают, что
Формула Друде
Формула Друде выводится из кинетического уравнения Больцмана и имеет вид:
Здесь m * - эффективная масса электрона, τ - время релаксации, то есть время, за которое электрон "забывает" о том, в какую сторону двигался после соударения.
Друде вывел закон Ома для токов в металле:
Опыт Толмена и Стюарта
В 1916 году опыт Толмена и Стюарта дал прямое доказательство тому, что носителями тока в металлах являются электроны.
Суть опыта была в следующем.
Опыт Толмена и Стюарта
Проводящая катушка с проводом длиной L вращалась вокруг своей оси с большой скоростью, а ее концы были замкнуты на гальванометр. Когда катушку резко тормозили, свободные электроны в металле продолжали двигаться по инерции, и гальванометр регистрировал импульс тока.
Считая, что свободные электроны подчиняются законам механики Ньютона, можно записать, что при остановке проводника электрон приобретает ускорение v ' (в катушке направлено вдоль проводов). При этом на электрон действует сила, направленная противоположно ускорению.
Под воздействием этой силы электрон ведет себя так, как если бы на него действовало поле E = - m v ' q . Эдс, возникающую в катушке при торможении можно записать, как:
ε = ∫ L E d l = - m v ' q ∫ L d l = - m v ' q L
Считая, что ускорение одинаково в каждом витке, можно записать закон Ома для катушки, а затем вычислить заряд, проходящий в ней за время d t :
d q = I d t = - m L d v q R d t d t = - m L d v q R
Заряд, прошедший от момента начала торможения до остановки:
q = - m L q R ∫ v 0 0 d v = - m L v 0 q R
Опыт Толмена и Стюарта получил хорошее согласование с теорией, полученное экспериментально отношение q m соответствовало отношению заряда электрона к его массе.
При T = 300 К вычислите среднюю скорость теплового движения свободных электронов.
Металлы, диэлектрики и полупроводники по зонной теории
Зонная теория позволила с единой точки зрения истолковать существование металлов, диэлектриков и полупроводников, объясняя различие в их электрических свойствах, во-первых, неодинаковым заселением электронами разрешенных зон, и во-вторых, шириной запрещенных зон.
Рассматривая заполнение электронами разрешенных зон необходимо использовать два правила: 1) Электроны стремятся занять самые низкие энергетические уровни. 2) Принцип Паули: на одном энергетическом уровне не может быть более двух электронов. Эти электроны должны иметь разные спины.
Степень заполнения электронами энергетических уровней в зоне определяется заполнением соответствующего атомного уровня. Если уровень атома полностью заполнен, то и зона полностью заполнена. Из незанятых уровней образуются свободные зоны, из частично заполненных – частично заполненные зоны. В общем случае можно говорить о валентной зоне, которая полностью заполнена и образовалась из энергетических уровней внутренних электронов свободных атомов и о зоне проводимости (свободной зоне), которая либо частично заполнена, либо свободна и образована из энергетических уровней внешних коллективизированных электронов изолированных атомов (рис.2).
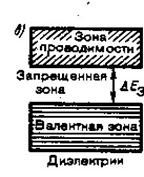 | Самая верхняя зона целиком занятая электронами (при Т=0 К) называется валентной. Зона, заполненная электронами частично (при Т = 0 К), называется зоной проводимости. Определим изменение энергии электрона, находящегося на некотором уровне в разрешенной зоне, под действием внешнего поля с напряженностью . Энергия приобретаемая электроном на длине свободного пробега , где - средняя длина свободного пробега электрона в кристалле равная примерно 10 -8 м в электрическом поле с напряженностью В/м, которая соответствует обычным источникам тока, эВ. |
| Рис.2. |
Это означает, что возможны только внутризонные переходы, так как междузонные переходы имеют много большую энергию. Необходимым условием электрической проводимости является наличие в разрешенной зоне свободных энергетических уровней на которые электрическое поле сторонних сил могло бы перевести электроны. В зависимости от степени заполнения зон электронами и ширины запрещенной зоны возможны три случая, изображенных на рис.3.
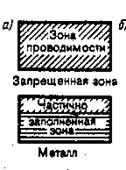   |
| (а) (б) (в) |
| Рис.3 |
3а). Зона проводимости заполнена лишь частично., то есть в ней имеются вакантные уровни. В этом случае электроны, получив сколь угодно малую энергетическую добавку (от поля или теплового движения) переходят на более высокий энергетический уровень той же зоны, то есть они участвуют в проводимости. Такой переход возможен, так как 1 К = 10 -4 эВ, что много больше расстояния между уровнями равному 10 -22 эВ. Таким образом, если в твердом теле имеется зона, лишь частично заполненная электронами, то это тело всегда будет проводником электрического тока. Именно это свойственно металлам.
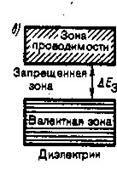
3б). Возможно также такое перераспределение электронов между зонами, возникающими из уровней различных атомов, которое привело к тому, что вместо двух частично заполненных зон кристалла окажется одна целиком заполненная (валентная) зона и одна свободная зона (зона проводимости). Твердые тела, у которых энергетический спектр электронных состояний состоит только из валентной зоны и зоны проводимости, являются диэлектриками или полупроводниками в зависимости от ширины запрещенной зоны. Если ширина запрещенной зоны кристалла порядка нескольких электрон –вольт, то тепловое движение не может перебросить электроны из валентной зоны в зону проводимости и кристалл является диэлектриком, оставаясь им при всех реальных температурах.
3в). Если запрещенная зона достаточно узка ( эВ), то переход электронов из валентной зоны в зону проводимости может быть осуществлен сравнительно легко путем теплового возбуждения, либо за счет внешнего источника, способного передать электронам энергию , и кристалл является полупроводником.
Различие между металлами и диэлектриками с точки зрения зонной теории состоит в том, что при 0 К в зоне проводимости металлов имеются электроны, а в зоне проводимости диэлектриков они отсутствуют. Различие же между диэлектриками и полупроводниками определяется шириной запрещенных зон: для диэлектриков она довольно широка (например для NaCl =6 эВ), а для полупроводников достаточно узка (для германия =0,72 эВ). При температурах близких к 0 К полупроводники ведут себя как диэлектрики, то есть переброс электронов в зону проводимости не происходит.
Сущность зонной теории проводимости заключается в следующем:
1). При объединении атомов в кристалл твердого тела возникают энергетические зоны.
2). Ширина запрещенных зон и характер заполнения электронами разрешенных зон обуславливают электрические свойства твердого тела – оно может быть или металлом, или полупроводником, или диэлектриком.
Читайте также:
