Металлическая поверхность работа выхода электронов которой равна
Электроны проводимости в кристалле находятся в потенциальной яме. Выход из нее требует совершения работы по преодолению силы, действующей на электрон со стороны кристалла. Найдем эту силу. Обладая энергией теплового движения, электроны могут выскакивать из кристалла на расстояние в несколько периодов. Вышедший из кристалла и находящийся у его поверхности на расстоянии х электрон индуцирует в металле заряд е+ (рис.97). Этот наведенный заряд действует на вышедший электрон так, как если бы он был сосредоточен под поверхностью металла на глубине х в точке, симметричной той, в которой находится электрон (см. Эл-во §5). Индуцированный заряд е+ называется электрическим изображением заряда е-. Оба точечные заряда притягиваются друг к другу с силой Кулона . (14.1)
Но это и есть сила притяжения металлом вышедшего из него электрона. Под действием этой силы электрон втягивается обратно в металл. Чтобы удалить электрон из металла, надо совершить работу по преодолению этой силы, перемещая электроны на бесконечность из точки, расположенной на расстоянии х0 от поверхности металла. В качестве х0 можно взять межатомное расстояние.
На рис.98 показана зависимость потенциальной энергии электрона от расстояния х до атомной плоскости – стенки металла. Энергетическое расстояние еj от уровня Ферми до нулевого уровня называют термодинамической работой выхода электрона, величину j – потенциалом выхода. Уровень Ес обозначает дно зоны проводимости, где Е = 0. У металлов работа выхода еj заключена в пределах 1,8 ¸ 5,3 эВ. Меньше всего она у щелочных металлов, больше – у золота, серебра, платины (табл. 14.1).
| Таблица 14.1 | |||
| Металл | еj, эВ | Металл | еj, эВ |
| Литий Li | 2,38 | Платина Pt | 5,32 |
| Натрий Na | 2,35 | Ванадий V | 4,58 |
| Калий К | 2,22 | Вольфрам W | 4,54 |
| Рубидий Rb | 2,16 | Золото Au | 4,30 |
| Цезий Cs | 1,18 | Серебро Ag | 4,30 |
Большое влияние на работу выхода оказывают мономолекулярные адсорбированные слои. Например, слой атомов цезия Cs на вольфраме W (рис.99). Цезий щелочной металл. Его внешний, валентный электрон связан с ядром значительно слабее, чем валентные электроны в вольфраме. Поэтому атомы цезия отдают вольфраму свои валентные электроны и превращаются в положительные ионы. Между этими ионами и их электрическими изображениями в вольфраме возникает сила притяжения, удерживающая ионы цезия на поверхности вольфрама. Поле этого двойного электрического слоя помогает выходу электронов из вольфрама. По этому в присутствии слоя цезия работа выхода электрона из вольфрама уменьшается с 4,54 эВ до 1,38 эВ. Подобно цезию действуют одноатомные слои бария Ba, церия Cе, тория Th и др.
2. Термоэлектронная эмиссия.
С повышением температуры металла поверхность Ферми разрыхляется, энергия электронов увеличивается, и они поднимаются на более высокие уровни (рис.100). Соответственно уменьшается работа выхода электронов. Поэтому концентрация вылетевших из кристалла электронов в пристеночном слое растет. Процесс испускания электронов нагретым металлом называется термоэлектронной эмиссией.
Формально термоэлектронная эмиссия есть всегда, когда Т > 0 К. Но заметной она становится при температурах Т > 800 К.
Облако термоэлектронов находится в динамическом равновесии. Число вылетевших из металла электронов в каждый промежуток времени примерно равно числу электронов, втянутых в металл. Поэтому суммарный ток эмиссии равен нулю.
На основе термоэлектронной эмиссии построен ламповый вакуумный диод (рис.101). Здесь К – катод, обычно нагреваемая вольфрамовая спираль, А – анод, холодная металлическая пластина обычно цилиндрической формы. По оси этого цилиндра натягивается спираль катода. Оба электрода помещаются в стеклянный сосуд с высоким вакуумом.
Если между катодом и анодом создавать электрическое поле с напряжением U, как показано на рис.101, то термоэлектроны под действием этого поля будут перемещаться от катода к аноду. Возникает электрический ток в вакууме. Вольтамперная характеристика вакуумного диода показана на рис.102. С повышением анодного напряжения U ток I через анод растет почти пропорционально U. Но при достижении некоторого значенья Iнас перестает увеличиваться. Это предельное значение Iнас называют ток насыщением. Он возникает тогда, когда все электроны, вылетевшие из нагретого катода, захватываются полем и переносятся к аноду.
С повышением температуры катода ток насыщения увеличивается. Разделив ток насыщения на поверхность S катода, получаем плотность тока насыщения jнас = iнасçS. В 1901г. Оуэн Ричардсон, исходя из классических представлений, теоретически нашел зависимость плотности тока насыщения от температуры поверхности катода. Уточненная Дешманом в 1923г. с учетом квантовых представлений, зависимость jнас(Т) имеет вид: . Формула Ричардсона-Дэшмана (14.2)
Здесь еj – работа выхода, А – константа, имеющая разное значение у разных металлов и колеблющаяся около теоретического значения А= 1,2·10 6 Аç(м 2 К 2 ).
3. Контактная разность потенциалов.
Рассмотрим процессы, происходящие при контакте двух разных металлов. Допустим, до электрического контакта металл 1 (на рис.103 слева) имеет работу выхода еj1, а работа выхода металла 2 больше, j2 > j1.
Приведем металлы в состояние электрического контакта, то есть сблизим их до такого расстояния, при котором возможен эффективный обмен электронами. Поскольку работа выхода электронов из металла 2 больше, то уровень Ферми в металле 2 ниже, чем в металле 1. В результате электроны проводимости с уровня Ферми металла 1 начинают переходить на уровень Ферми металла 2.
В результате такого перехода электронов металл 2 заряжается отрицательно, энергия электронов и, соответственно, уровень Ферми в нем повышаются. Металл 1 заряжается положительно, энергия электронов и уровень Ферми в нем понижаются. Между металлами возникает контактная разность потенциалов j12.
Суммарное перетекание зарядов прекратится, когда уровни Ферми сравняются, а разность потенциалов между проводниками будет равна разности потенциалов выхода, j12 = j2 - j1, и встречные потоки электронов сравняются n21=-n12 (рис.103 справа). Контактная разность потенциалов между проводниками создает для электронов, переходящих в проводник с большей работой выхода, потенциальный барьер высотой еj12.
Оценим количество электронов, перетекающих из одного металла в другой при возникновении контактной разности потенциалов j12. Будем считать, что между контактирующими металлами остается зазор шириной d, а заряды концентрируются на контактирующих поверхностях. Тогда заряд Q на каждой из поверхностей, необходимый для создания напряжения j12, найдется из формулы плоского конденсатора, . (14.3)
Как видно из таблицы 14.1, контактная разность потенциалов В. Расстояние d между металлами не может быть меньше параметра решетки а » 0,3 нм. Полагая j12 =1 В и d = 0,3 нм, получаем максимальную плотность заряда на контактирующих поверхностях.
Разделив на заряд электрона получаем, что на 1 м 2 поверхности приходится 2·10 17 электронов. Если диаметр атомов взять равным постоянной решетки а = 0,3 нм, то на 1 м 2 поверхности в одноатомном слое металла размещается атомов. Если атомы металла содержат по одному валентному электрону, то для создания контактной разности потенциалов 1 В потребовалось всего лишь (2×10 17 ç10 19 )´100% = 2% электронов проводимости одноатомного поверхностного слоя.
4. Закон Вольта.
Контактную разность потенциалов открыл в девяностых годах XVIII века итальянец Александр Вольта. В серии экспериментов 1792–1794 годов он установил, что в цепочке из ряда последовательно соединенных металлов контактная разность потенциалов зависит лишь от крайних металлов. Этот опытный факт называется законом Вольта. Действительно, пусть имеется цепочка из металлов 1,2,3,4 (рис.104). Работа выхода металлов еj1, еj2, еj3, еj4. На границе каждой пары возникает контактная разность:
Просуммировав левые и правые части, получаем: . (14.5)
Сумма всех контактных ЭДС (левой части равенства) равна контактной ЭДС крайних металлов в цепочке (правая часть равенства). Если концы цепи замкнуть, то независимо от количества звенев сумма контактных разностей потенциалов равна нулю. Тока в цепи нет.
5. Термо-ЭДС.
Сумма контактных разностей потенциалов в замкнутой цепи равна нулю лишь при условии, что температуры всех контактов одинаковы. В 1821 г. Томас Зеебек, сжимая концы висмутовой и медной пластинок теплыми пальцами обнаружил, что если цепь замкнута, то в ней протекает ток. Это явление возникновения ЭДС в цепи из разных металлов при перепаде температур между спаями называют эффектом Зеебека или термоэлектричеством. В рамках классической электронной теории можно дать простое толкование явлению Зеебека и получить зависимость термо-ЭДС от перепада температур.
Пусть имеется замкнутая цепь из двух металлов 1 и 2 со спаями A и B (рис.105). Полагаем, что электроны проводимости на верхних уровнях зоны проводимости распределяются в силовом поле решетки по закону Больцмана.
Здесь n01 и n02 – концентрация электронов проводимости на уровнях Ферми. В силу полной заполняемости этих уровней будем полагать n01 = n02; U1 и U2 – потенциальная энергия электронов в металлах 1 и 2. Она может изменяться от нуля на уровне Ферми до еj (работа выхода) на нулевом уровне. Разделим первое уравнение на второе.
Разделив разность U1 –U2 на заряд электрона е, получаем концентрационную разность потенциалов между металлами 1 и 2. . (14.9)
Если температуры спаев ТА и ТB одинаковы, то концентрационная ЭДС в замкнутой цепи, так же, как контактная разность потенциалов, равна нулю. Тока в цепи нет. Если же температуры спаев разные, ТА ¹ ТB, то в цепи возникает термо-ЭДС (рис.106). Концентрационные перепады потенциалов в контактах А и B разные.
Учитывая грубость классических приближений, обычно выделяют лишь температурную зависимость, которая хорошо подтверждается опытом при малых перепадах температур, . (14.12)
Термо-ЭДС, возникающая в цепи из разных металлов, широко применяется для измерения температур в диапазоне от 0 К до » 1000°С. Соответствующее устройство из двух разных металлов называется термопарой. Один спай термопары поддерживается при постоянной температуре, например при 0 о С в сосуде с тающим льдом, другой помещают в ту среду, температуру которой хотят измерить. О величине температуры можно судить как по величине термотока, измеряемого гальванометром, так и более точно по величине термо-ЭДС, измеряемой методом компенсации. С помощью термопар можно измерять температуру с точностью до сотых долей градуса.
6. Эффект Пельтье,1834 г.
Он обратен эффекту Зеебека и состоит в том, что при пропускании тока по цепи из разных металлов один контакт у металла нагревается, другой охлаждается.
Пусть в цепи из двух разных металлов действует источник тока – батарея Б. В результате в цепи идет постоянный ток I (рис.107). Проходя спай B, электроны, идущие по цепи на рисунке против часовой стрелки, дополнительно ускоряются полем контактного потенциала. Их скорость дрейфа увеличивается, поэтому при столкновении с узлами электроны передают им большую, по сравнению со средней, энергию. Спай В нагревается больше, чем рядом расположенные участки проводников.
В спае А электроны тормозятся контактным полем, их скорость дрейфа уменьшается, поэтому спай А нагревается меньше, чем рядом расположенные участки проводов. Кроме того, для установления равновесия этих электронов с электронным газом им необходимо приобрести еще энергию. Эту энергию они черпают из решетки. В результате спай А охлаждается больше, чем нагревается. В итоге теплота в спае А поглощается.
Выделяющаяся или поглощающаяся теплота Пельтье QП в контакте пропорциональна заряду It, прошедшему через контакт. . (14.13)
Здесь П – коэффициент Пельтье связан с дифференциальной термо-ЭДС соотношением: П = аDT.(14.14)
Где DТ – разность температур между контактами.
Эффект Пельтье позволяет создавать малогабаритные холодильные устройства. Их особенность в том, что изменяя направление тока в цепи, можно один и тот же контакт заставить как поглощать тепло (холодильник), так и выделять его (нагреватель).
7. Эффект Томсона.
В 1853 – 54 г.г. Рудольф Клаузиус и Уильям Томсон независимо друг от друга применили к явлениям термоэлектричества принципы термодинамики. В процессе построения термодинамической теории термоэлектричества Томсон установил, что неравномерно нагретый проводник должен вести себя как система находящихся в контакте физически разнородных участков. На этом основании Томсон пришёл к заключению и подтвердил его экспериментально, что в однородном неравномерно нагретом проводнике должно выделяться или поглощаться тепло Пельтье (тепло Томсона). Само явление назвали эффектом Томсона.
Принципиальная схема экспериментальной установки изображена на рис.108
Концы двух одинаковых проводящих стержней помещены в два термостата с разными температурами Т1 и Т2. Допустим, Т1 > Т2. Тогда градиент температуры в верхнем стержне направлен по току I, а в нижнем – против тока. В результате в одном стержне выделяется тепло Томсона (его температура выше), а в другом – поглощается.
Знак эффекта у разных проводников разный. В висмуте и цинке, например, тепло выделяется, если поток тепла и электрический ток совпадают по направлению (на рисунке нижний проводник). А в Fe, Pt, Sb при тех же условиях тепло поглощается. С изменением направления тока знак эффекта во всех проводниках меняется.
Тепло Томсона Q, выделяющееся в проводнике, пропорционально перепаду температур ΔТ, току I, протекающему по проводнику, и времени t Q = σΔTIt.
Здесь σ – коэффициент Томсона. Он зависит от материала провода и от его температуры. Коэффициент σ невелик. У металлов он порядка 10 –5 ВçК. За положительное направление тока принимают направление градиента температур, то есть направление от холодного конца проводника к горячему. Если тепло при этих условиях выделяется (проводник нагревается), эффект Томсона считается положительным.
Количественно эффект Томсона исследовал в 1867 г. Франсуа Леру. В установке, собранной по схеме рис. 108, к поверхности стержней он присоединял спаи термопар. Пока тока через стержни не было, термоЭДС в цепи термопар была равна нулю. При включении тока через стержни появлялась термоЭДС, величина и знак которой позволяли определить коэффициент Томсона σ.
8. Закон Джоуля – Ленца в замкнутой цепи всегда выполняется. Суммарный эффект Пельтье и Томсона в замкнутой цепи равен нулю, поскольку наряду с участками цепи, где тепло Пельтье и Томсона выделяется, всегда есть участки, где такое же тепло поглощается.
Примеры решенных задач по физике на тему "Фотоэффект"
Ниже размещены условия задач и отсканированные решения. Если вам нужно решить задачу на эту тему, вы можете найти здесь похожее условие и решить свою по аналогии. Загрузка страницы может занять некоторое время в связи с большим количеством рисунков. Если Вам понадобится решение задач или онлайн помощь по физике- обращайтесь, будем рады помочь.
Явление фотоэффекта заключается в испускании веществом электронов под действием падающего света. Теория фотоэффекта разработана Эйнштейном и заключается в том, что поток света представляет собой поток отдельных квантов(фотонов) с энергией каждого фотона h n . При попадании фотонов на поверхность вещества часть из них передает свою энергию электронов. Если этой энергия больше работы выхода из вещества, электрон покидает металл. Уравнение эйнштейна для фотоэффекта: где — максимальная кинетическая энергия фотоэлектрона.
Длина волны красной границы фотоэффекта для некоторого металла составляет 307 нм. Максимальная кинетическая энергия фотоэлектронов – 1 эВ. Найти отношение работы выхода электрона к энергии падающего фотона.

Частота света красной границы фотоэффекта для некоторого металла составляет 6*10 14 Гц, задерживающая разность потенциалов для фотоэлектронов – 2В. Определить частоту падающего света и работу выхода электронов.

Работа выхода электрона из металла составляет 4,28эВ. Найти граничную длину волны фотоэффекта.

На медный шарик радает монохроматический свет с длиной волны 0,165 мкм. До какого потенциала зарядится шарик, если работа выхода электрона для меди 4,5 эВ?

Работа выхода электрона из калия составляет 2,2эВ, для серебра 4,7эВ. Найти граничные длину волны фотоэффекта.


Длина волны радающего света 0,165 мкм, задерживающая разность потенциалов для фотоэлектронов 3В. Какова работа выхода электронов?
Красная граница фотоэффекта для цинка 310 нм. Определить максимальную кинетическую энергию фотоэлектронов, если на цинк падает свет с длиной волны 200нм.

На металл с работой выхода 2,4эВ падает свет с длиной волны 200нм. Определить задерживающую разность потенциалов.

На металл падает свет с длиной волны 0,25 мкм, задерживающая разность потенциалов при этом 0,96В. Определить работу выхода электронов из металла.

При изменении длины волны падающего света максимальные скорости фотоэлектронов изменились в 3/4 раза. Первоначальная длина волны 600нм, красная граница фотоэффекта 700нм. Определить длину волны после изменения.


Работы выхода электронов для двух металлов отличаются в 2 раза, задерживающие разности потенциалов - на 3В. Определить работы выхода.

Максимальная скорость фотоэлектронов равно 2,8*10 8 м/с. Определить энергию фотона.
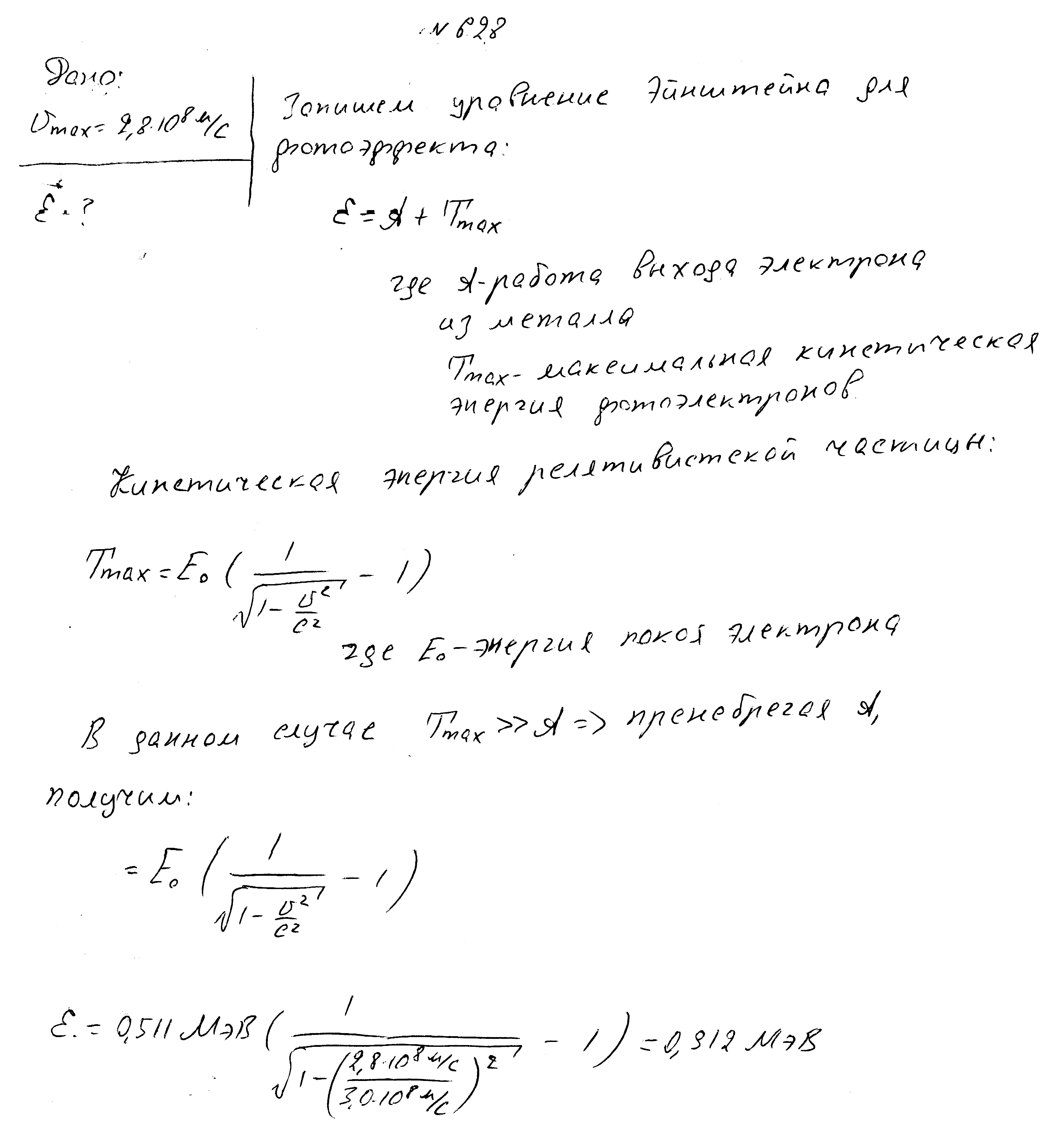
Энергии падающих на металл фотонов равны 1,27 МэВ. Найти максимальную скорость фотоэлектронов.

Максимальная скорость фотоэлектронов равно 0,98с, где с - скорость света в вакууме. Найти длину волны падающего света.
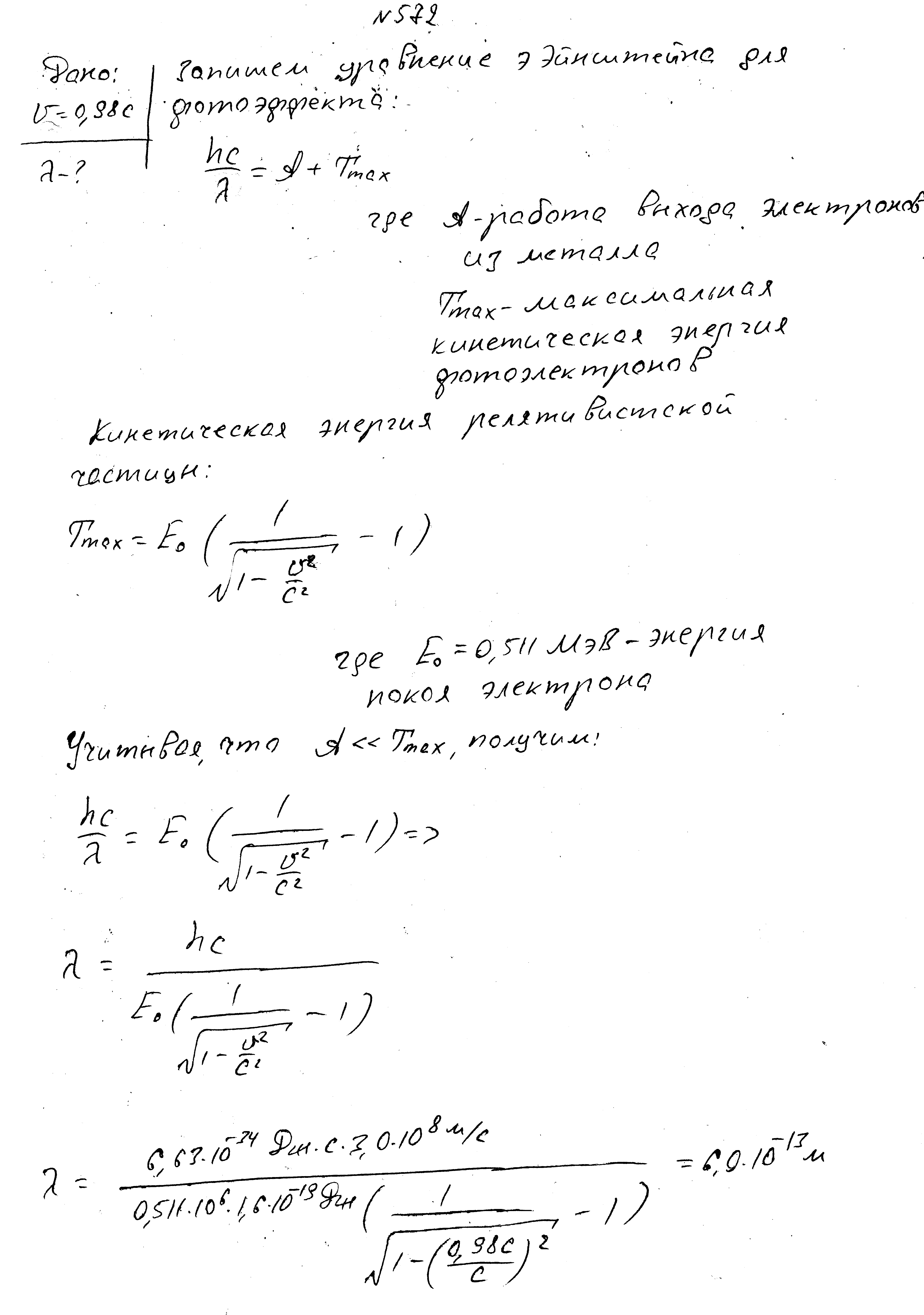
Энергия фотона в пучке света, падающего на поверхность металла, равно 1,53 МэВ. Определить максимальную скорость фотоэлектронов.
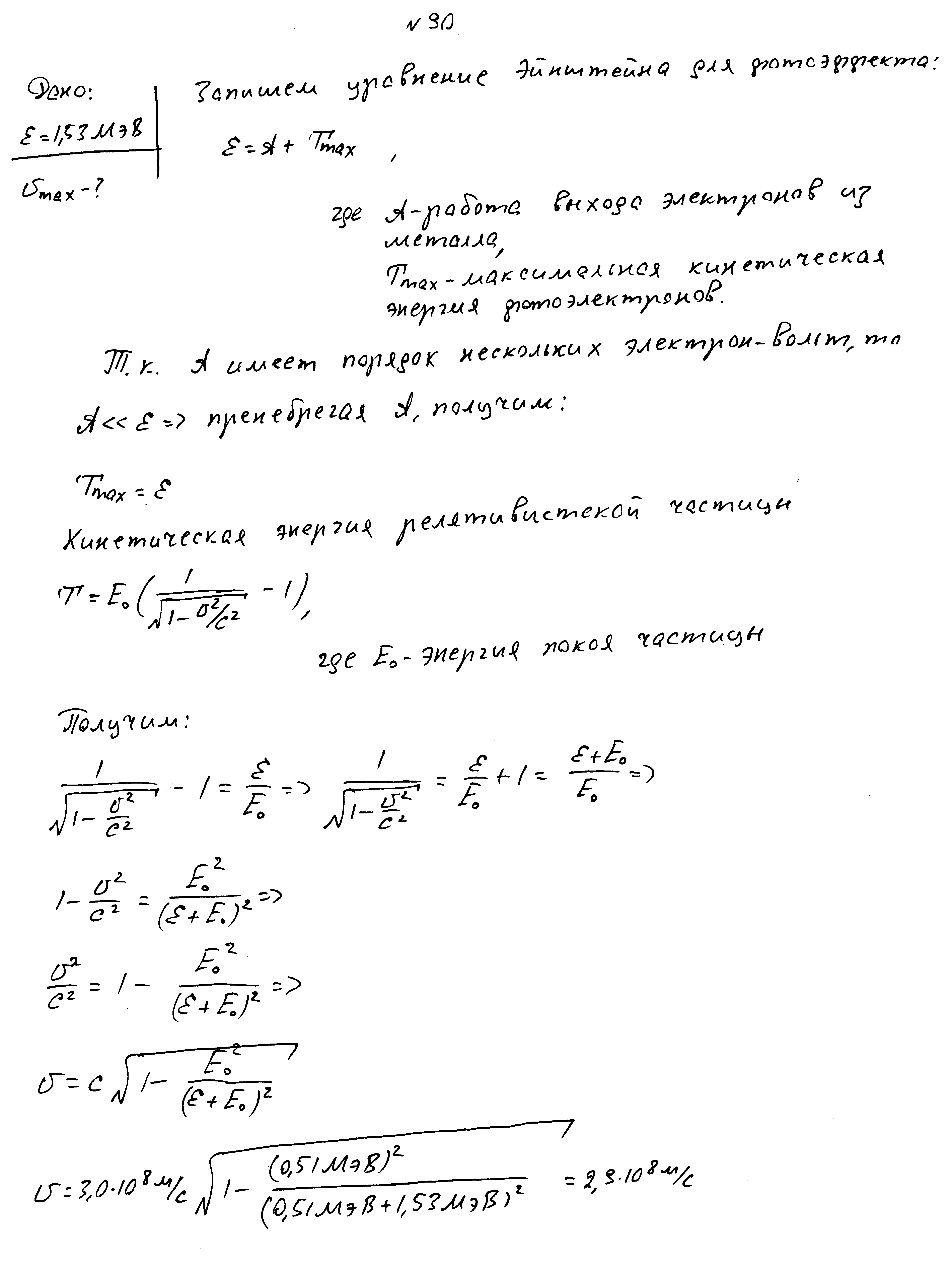
На шарик из металла падает свет с длиной волны 0,4 мкм, при этом шапик заряжается до потенциала 2В. До какого потенциала зарядится шарик, если длина волны станет равной 0,3 мкм?

После изменения длины волны падающего света в 1,5 раза задерживающая разность потенциалов изменилась с 1,6В до 3В. Какова работа выхода?
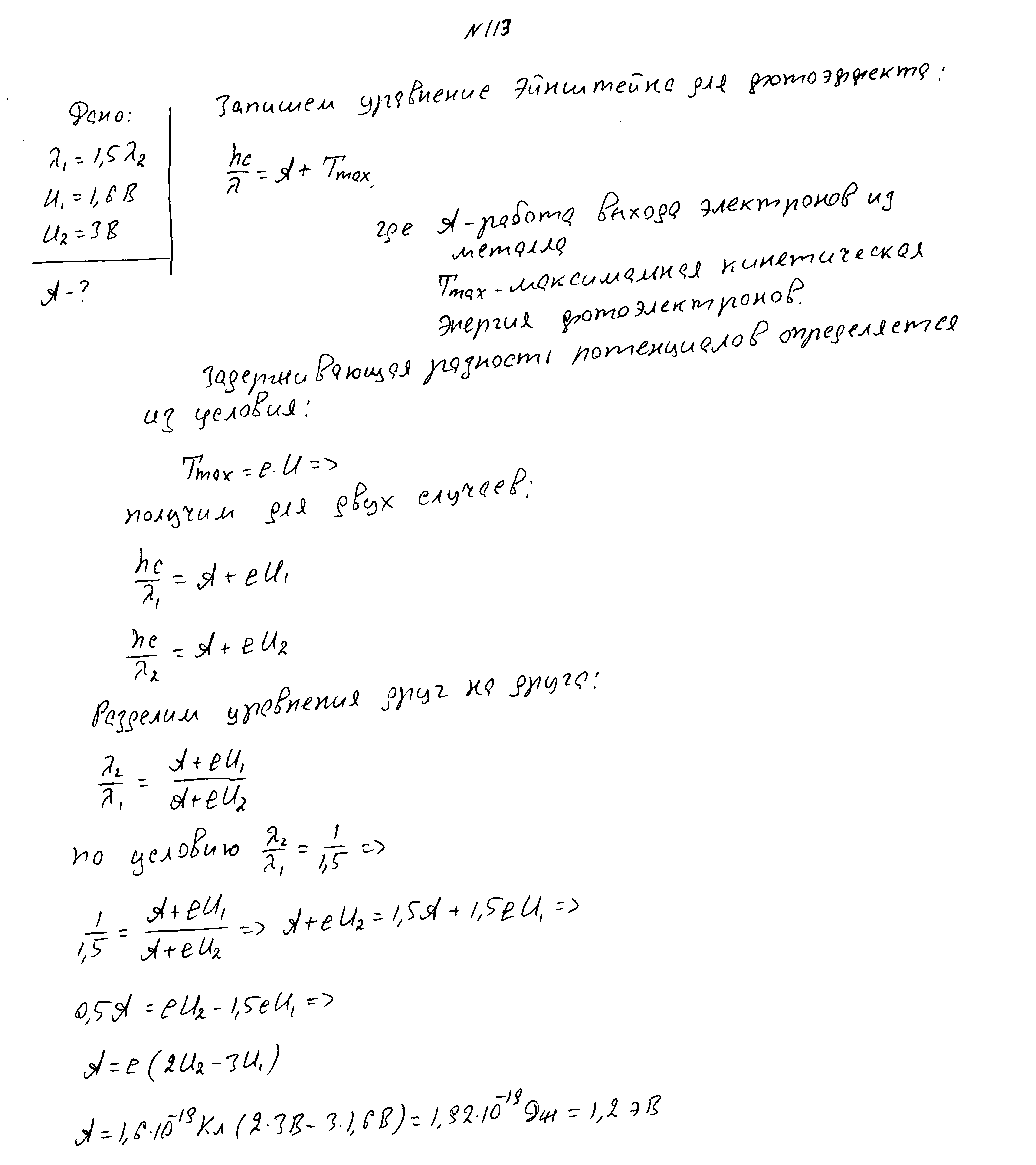
Красная граница фотоэффекта 560нм, частота падающего света 7,3*10 14 Гц. Найти максимальную скорость фотоэлектронов.
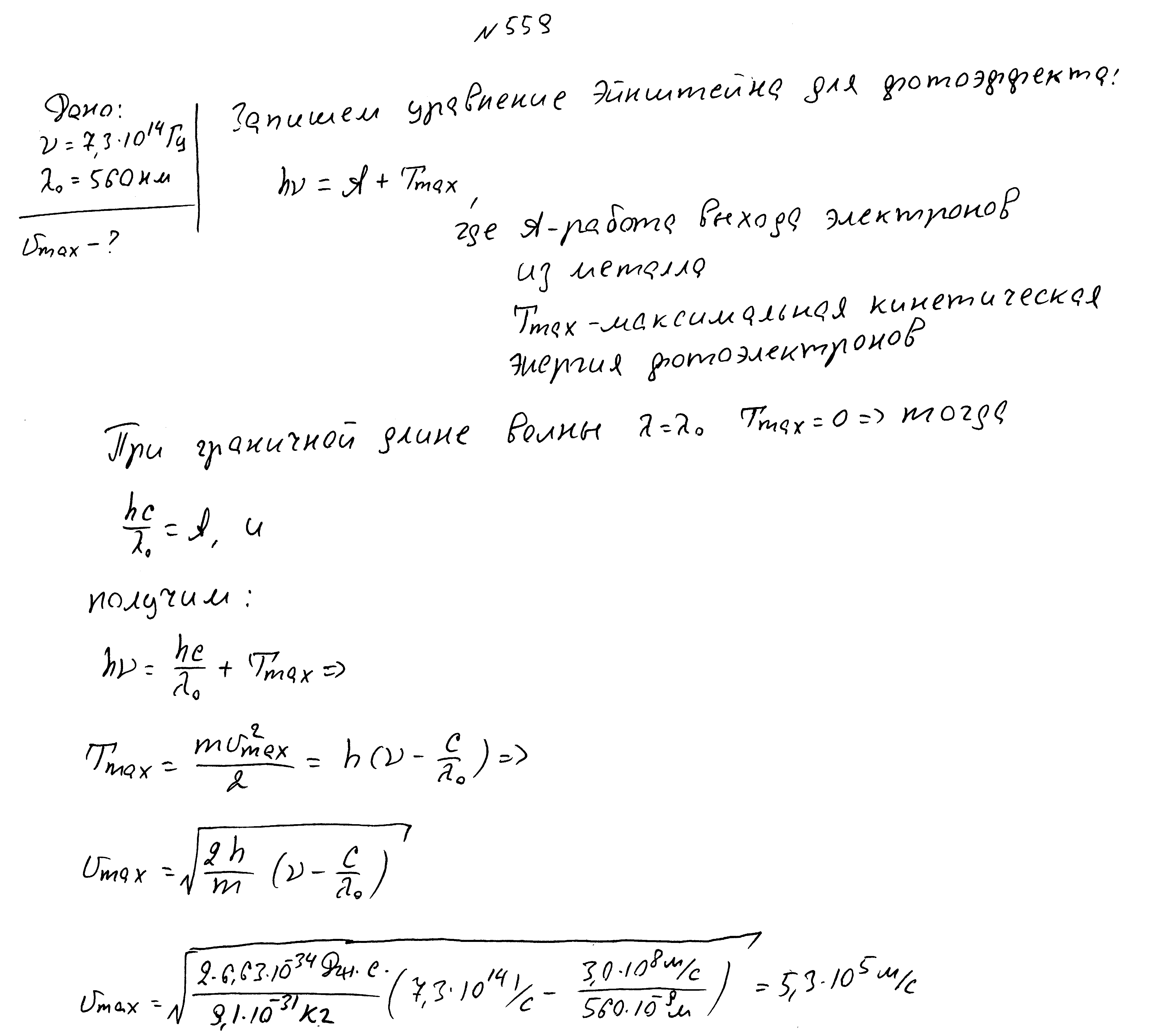
Красная граница фотоэффекта 2800 ангстрем, длина волны падающего света 1600 ангстрем. Найти работу выхода и максимальную кинетическую энергию фотоэлектрона.

Задерживащая разность потенциалов 1,5В, работа выхода электронов 6,4*10 -19 Дж. Найти длину волны падающего света и красную границу фотоэффекта.

Работа выхода электронов из металла равна 3,3 эВ. Во сколько раз изменилась кинетическая энергия фотоэлектронов. если длина волны падающего света изменилась с 2,5*10 -7 м до 1,25*10 -7 м?
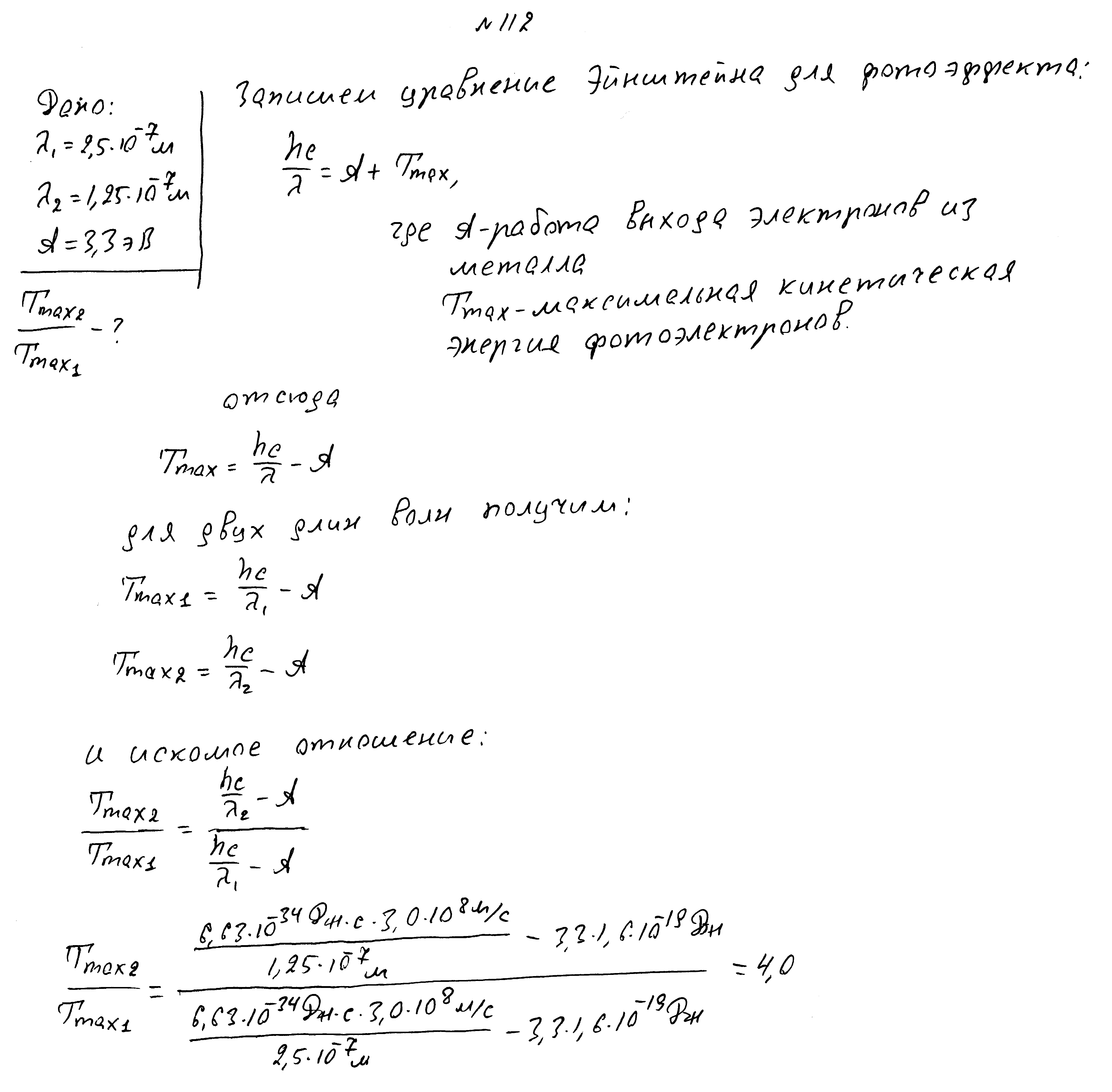
Найти максимальную скорость фотоэлектронов для видимого света с энергией фотона 8 эВ и гамма излучения с энергией 0,51 МэВ. Работа выхода электронов из металла 4,7 эВ.
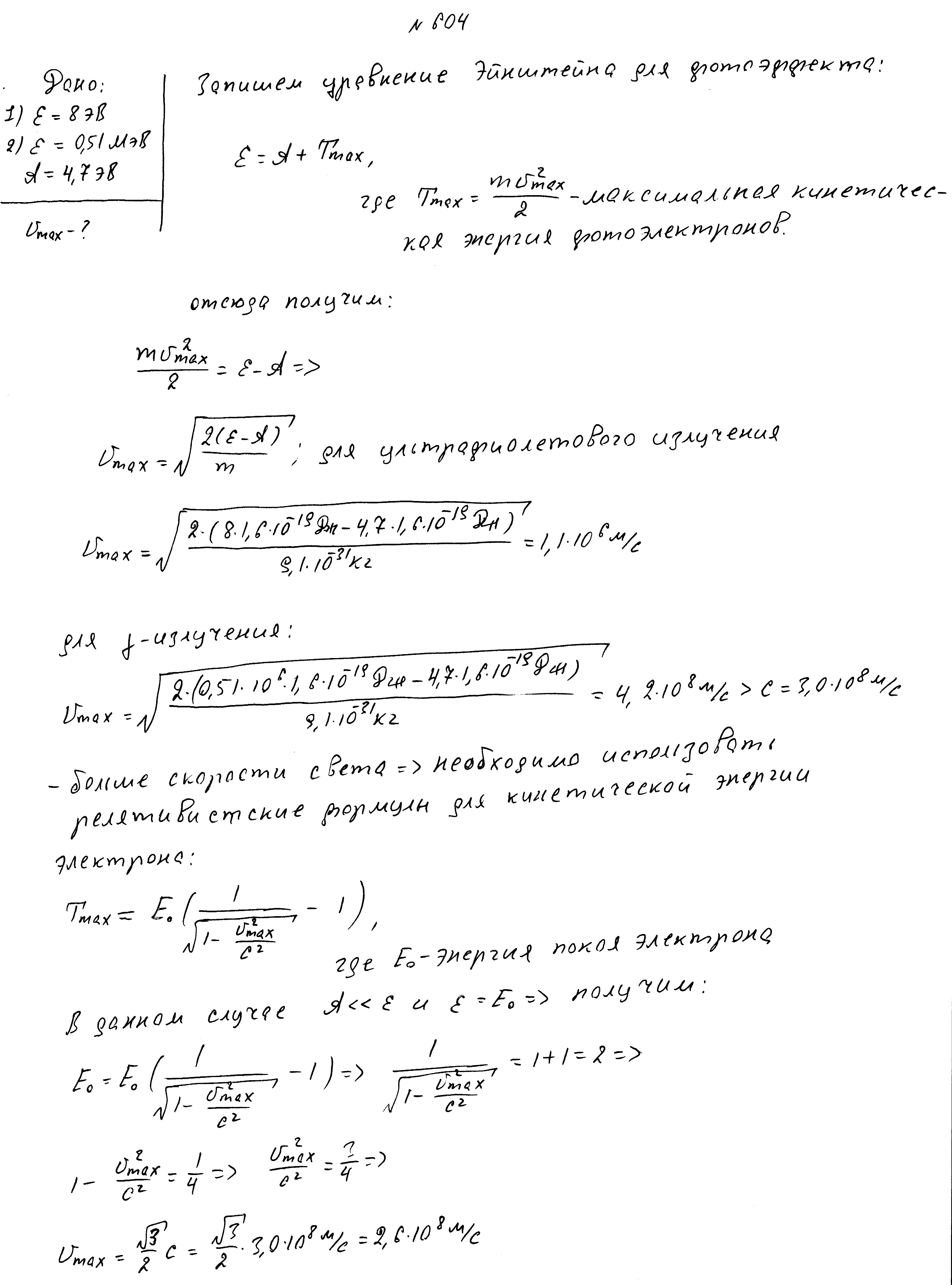
Фототок прекращается при задерживающей разности потенциалов 3,7 В. Работа выхода электронов равна 6,3 эВ. Какая работа выхода электронов у другого металла, если там фототок прекращается при разности потенциалов, большей на 2,3В.
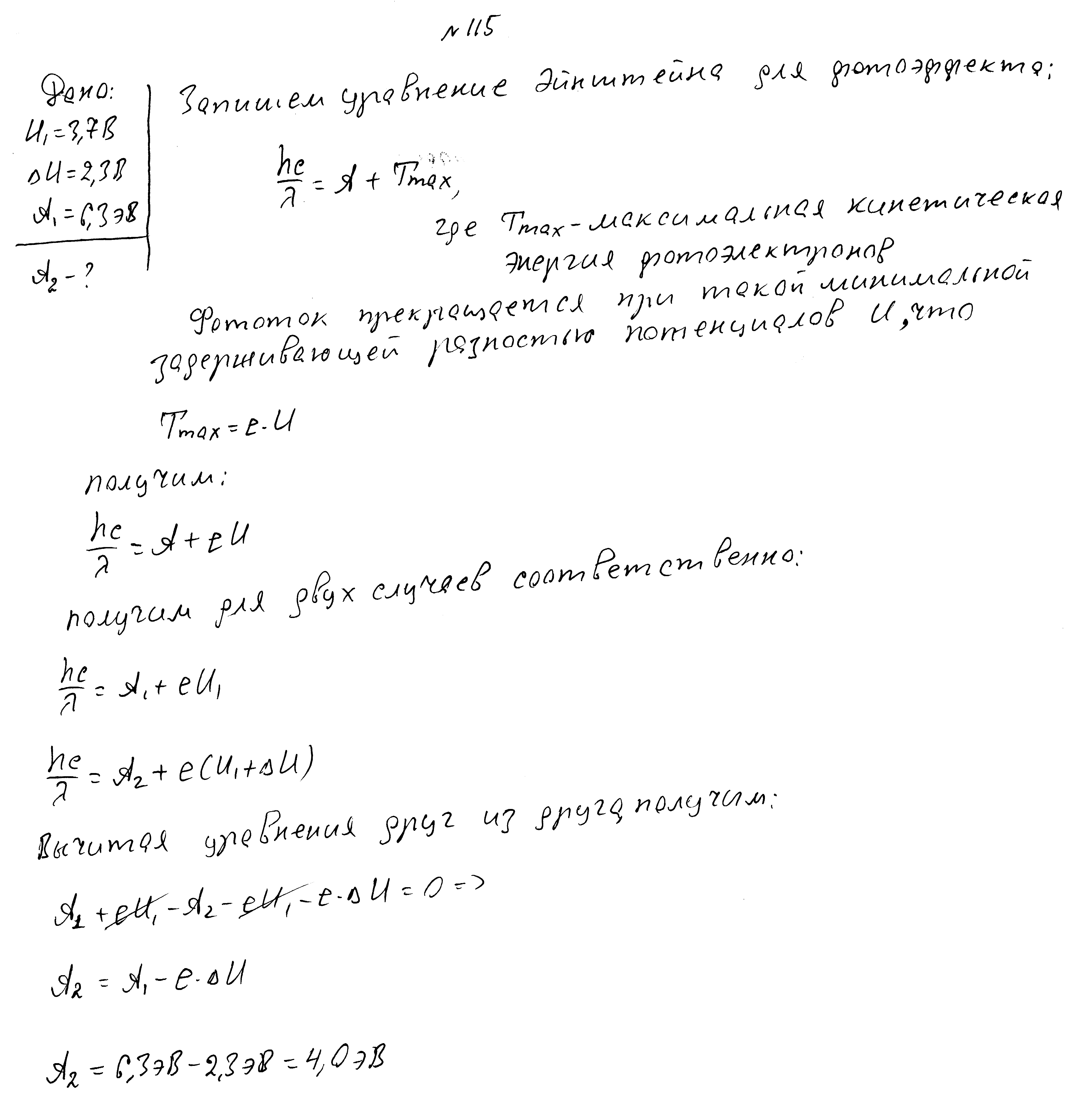
Работа выхода электронов из металла 4,5 эВ, энергия падающих фотонов 4,9 эВ. Чему равен максимальный импульс фотоэлектронов?
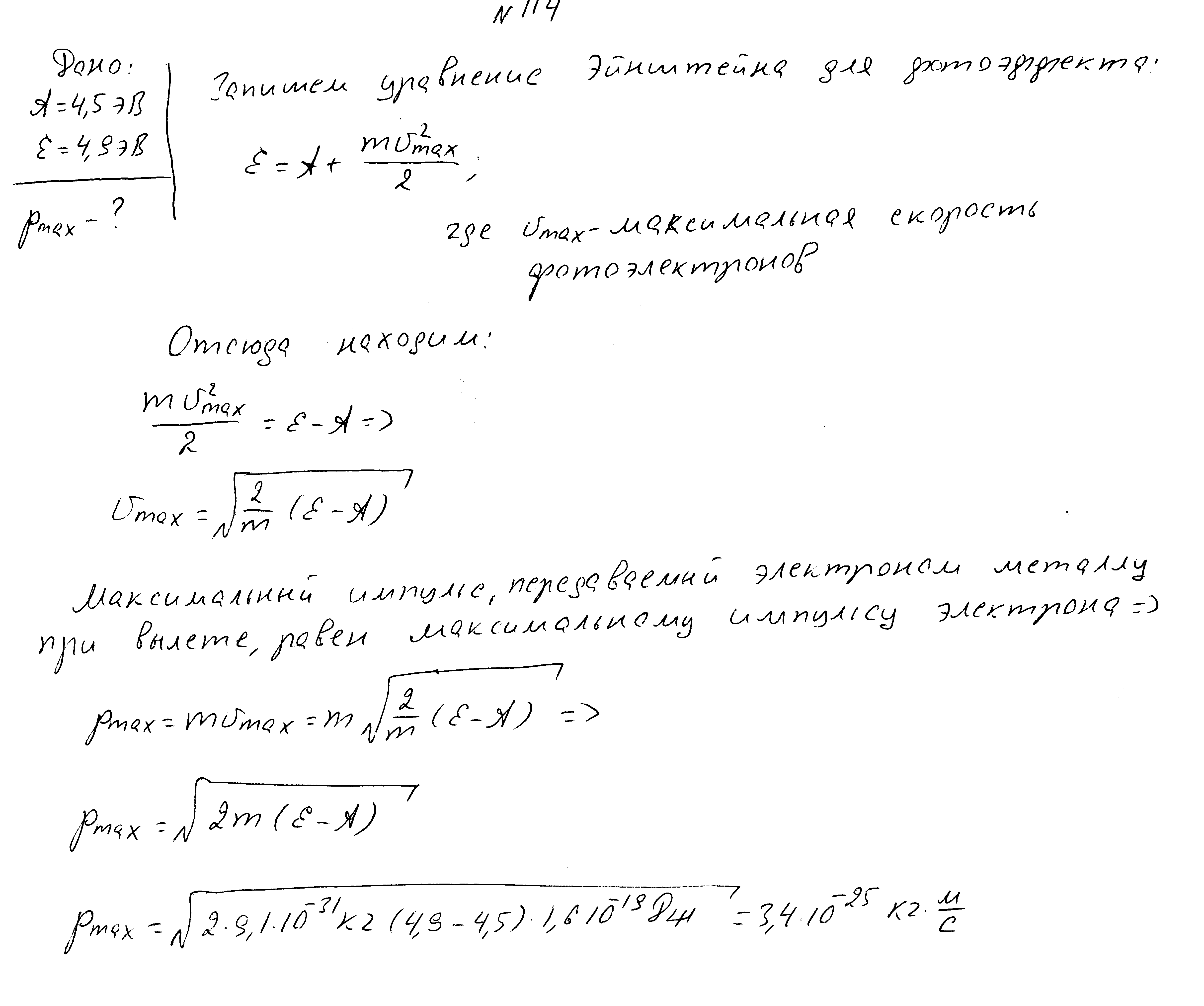
Красная граница фотоэффекта 2900 ангстрем, максимальная скорость фотоэлектронов 10 8 м/с. Найти отношение работы выхода электронов к энергии палающих фотонов.
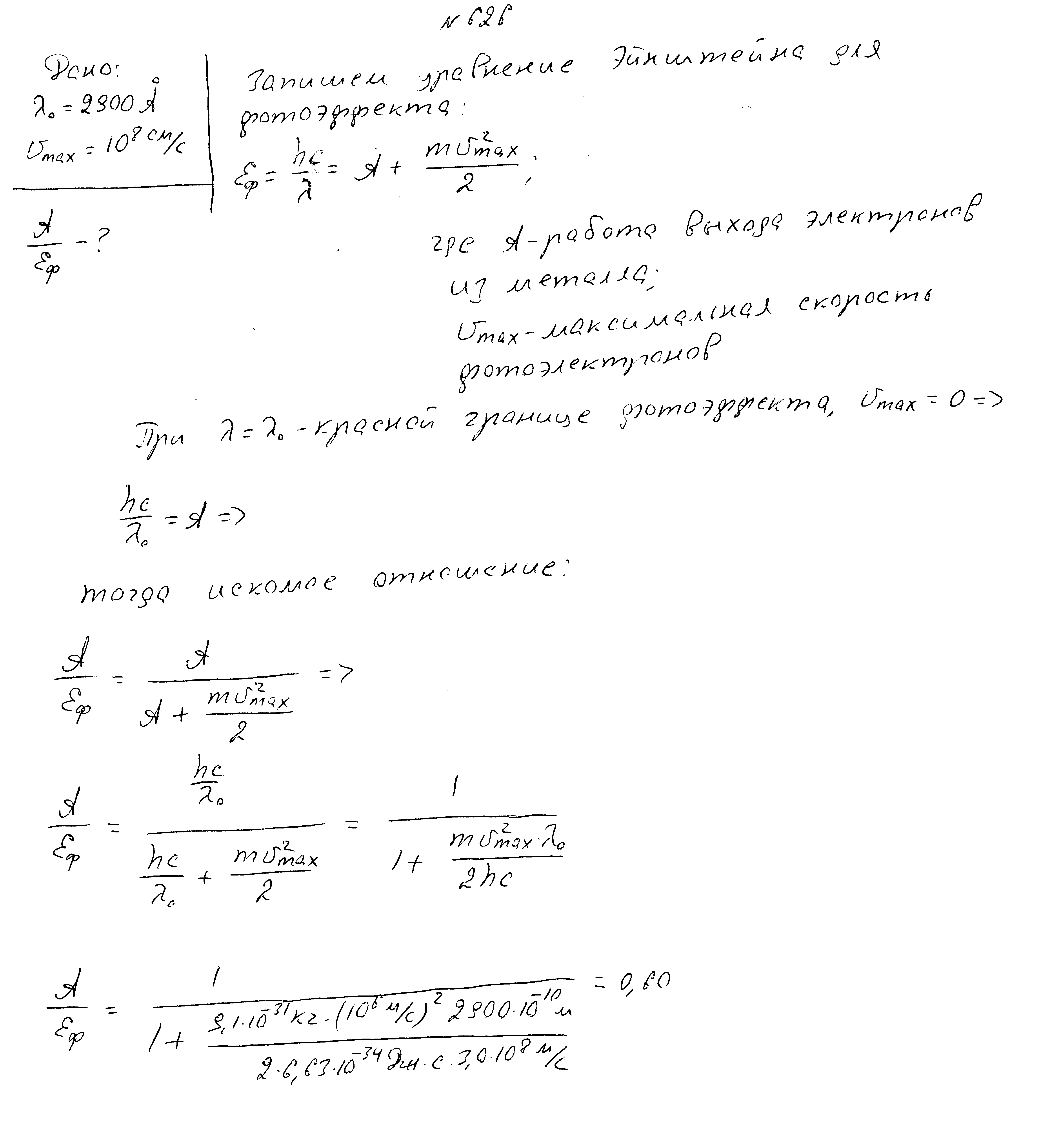
Длина волны падающего света 400нм, красная граница фотоэффекта равна 400нм. Чему равна максимальная скорость фотоэлектронов?
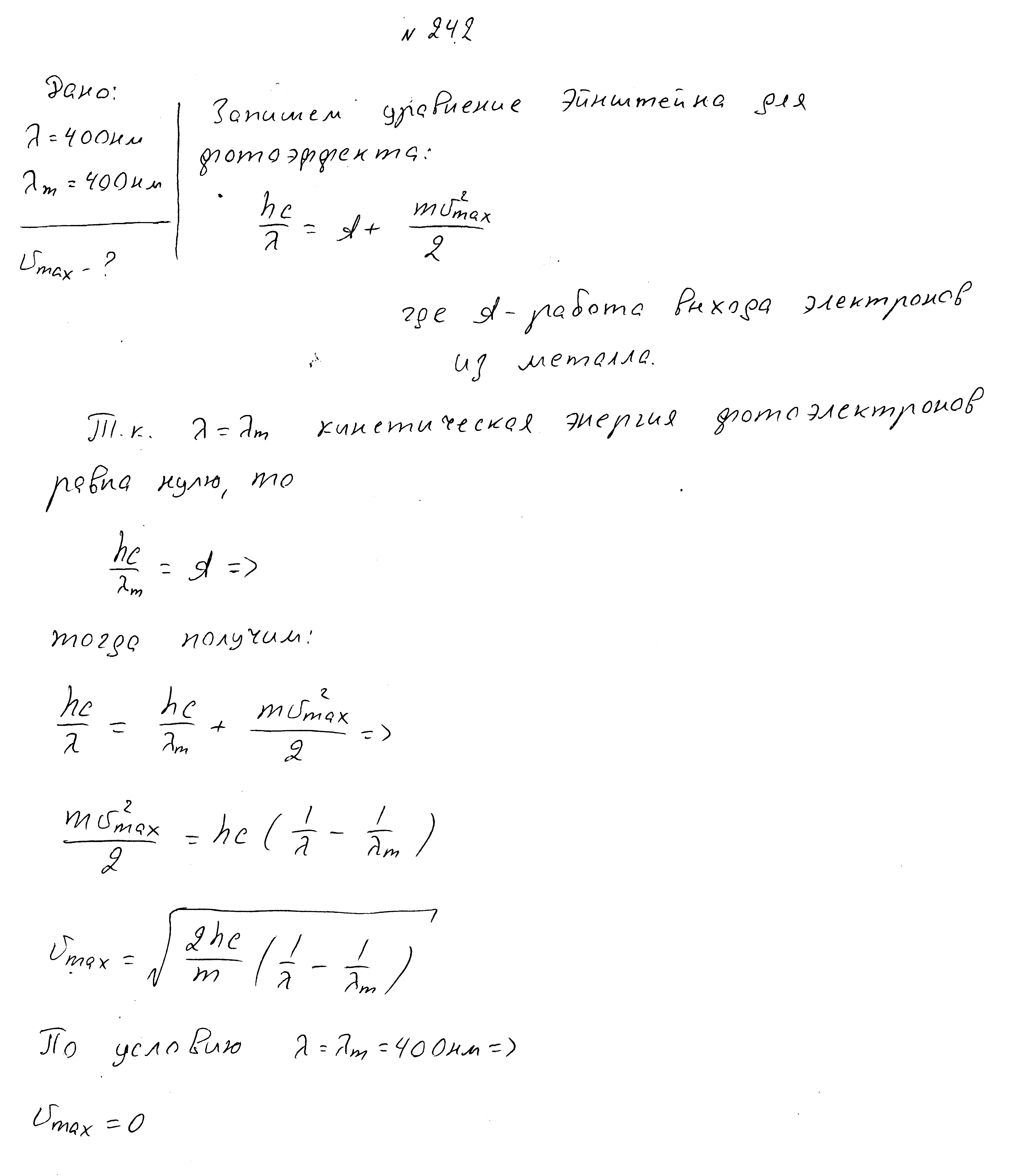
Длина волны падающего света 300нм, работа выхода электронов 3,74 эВ. Напряженность задерживающего электростатического поля 10 В/см.Какой максимальный путь фотоэлектронов при движении в направлении задерживающего поля?
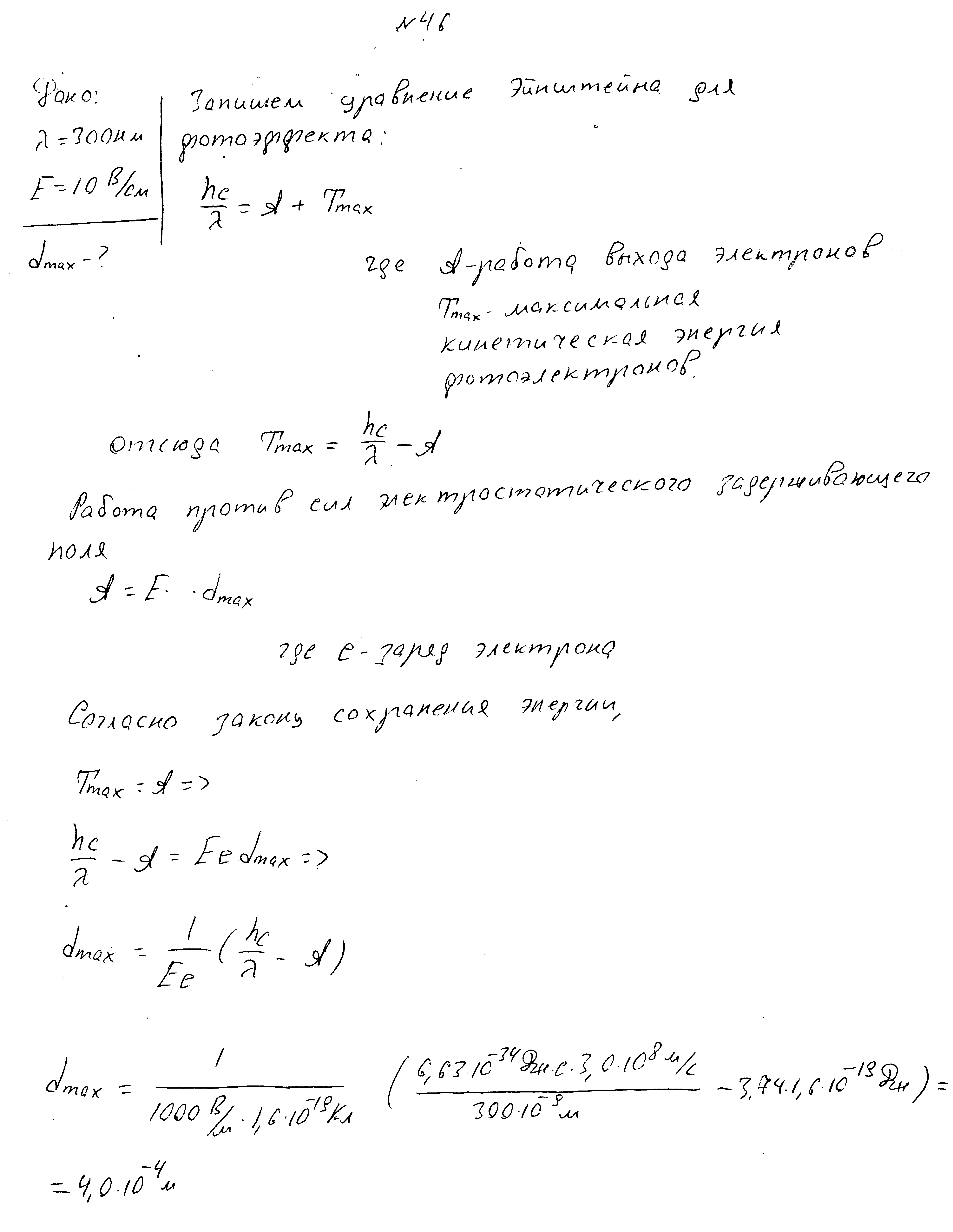
Длина волны падающего света 100 нм, работа выхода электронов 5,30эВ. Найти максимальную скорость фотоэлектронов.
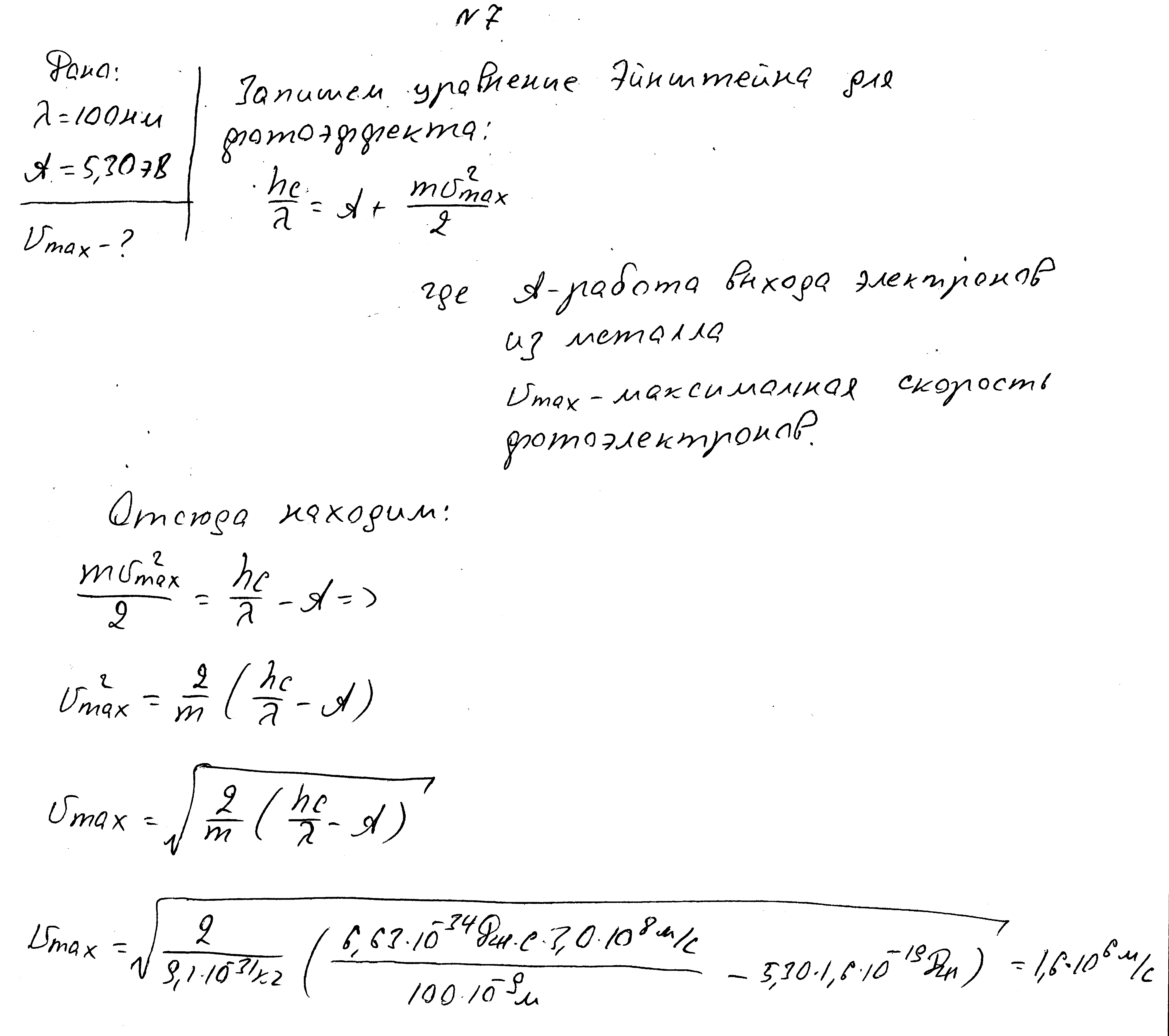
При длине волны радающего света 491нм задерживающая разность потенциалов 0,71В. Какова работа выхода электронов? Какой стала длина волны света, если задерживающая разность потенциалов стала равной 1,43В?
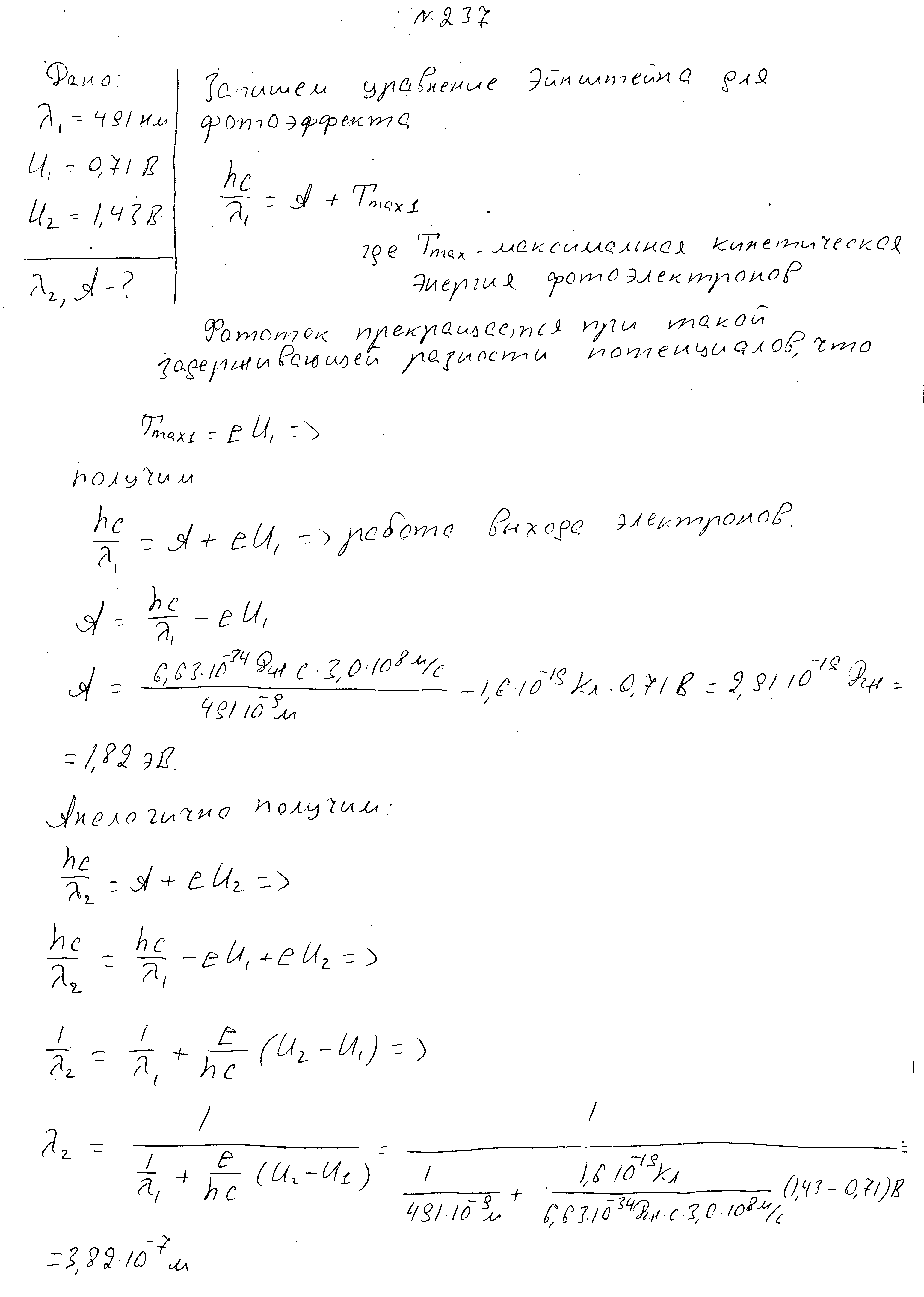
Кинетическая энергия фотоэлектронов 2,0 эВ, красная граница фотоэффекта 3,0*10 14 Гц. Определить энергию фотонов.

Красная граница фотоэффекта 0,257 мкм, задерживающая разность потенциалов 1,5В. Найти длину волны падающего света.
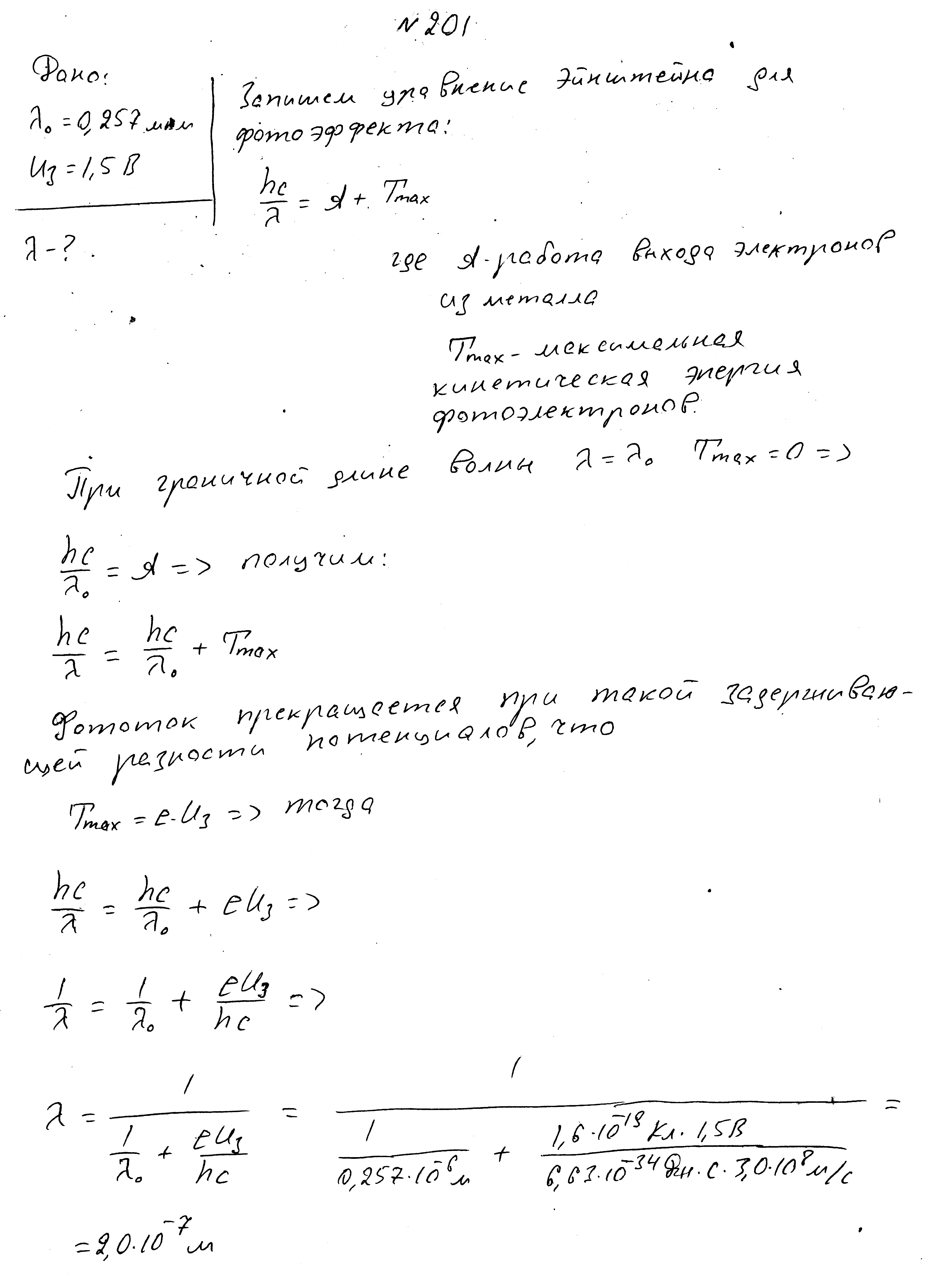
Красная граница фотоэффекта 2850 ангстрем. Минимальное значение энергии фотона, при котором возможен фотоэффект?

Ниже вы можете посмотреть обучаюший видеоролик на тему фотоэффекта и его законов.
Металлическая поверхность работа выхода электронов которой равна
Тип 19 № 27955Для проведения опытов по наблюдению фотоэффекта взяли пластину из металла с работой выхода 3,4 · 10 –19 Дж и стали освещать её светом частотой 6 · 10 14 Гц. Как изменится сила фототока насыщения Imax и работа выхода электронов с поверхности металла Авых, если увеличить интенсивность падающего света, не изменяя его частоту?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
При увеличении интенсивности падающего света увеличится количество фотонов, следовательно, увеличится число фотоэлектронов, что приведет к увеличению силы фототока насыщения (1).
Работа выхода электронов с поверхности металла зависит только от его свойств, поэтому от интенсивности света не зависит, т. е. не изменится (3).
Тип 20 № 28047Выберите все верные утверждения о физических явлениях, величинах и закономерностях. Запишите цифры, под которыми они указаны.
1) При торможении шайбы при ее движении по горизонтальной поверхности работа силы тяжести, действующей на шайбу, равна нулю.
2) Процесс диффузии может наблюдаться только в газах и жидкостях
3) При коротком замыкании внешней цепи идеальный амперметр, включенный в цепь, показывает силу тока, равную нулю.
4) В замкнутом проводящем контуре при изменении магнитного потока через ограниченную им площадку возникает индукционный ток.
5) Максимальная кинетическая энергия фотоэлектрона больше энергии кванта света, выбившего его с поверхности фотокатода, на величину работы выхода.
1) Верно. Так как сила тяжести перпендикулярна направлению перемещения шайбы, то работа этой силы равна нулю.
2) Неверно. Процесс диффузии может происходить как в газах и в жидкостях, так и в твердых телах.
3) Неверно. При коротком замыкании сила тока равна и значительно возрастает.
4) Верно. Вследствие явления электромагнитной индукции в замкнутом проводящем контуре при изменении магнитного потока через ограниченную им площадку возникает индукционный ток.
5) Неверно. Энергия фотона идет на работу выхода электронов с поверхности металла и на приобретение фотоэлектронами кинетической энергии. Вследствие этого Максимальная кинетическая энергия фотоэлектрона меньше энергии кванта света, выбившего его с поверхности фотокатода, на величину работы выхода.
Задания Д11 B20 № 2238При освещении металлической пластины с работой выхода А монохроматическим светом частотой происходит фотоэлектрический эффект, максимальная кинетическая энергия освобождаемых электронов равна Каким будет значение максимальной кинетической энергии фотоэлектронов при освещении этим же монохроматическим светом пластины с работой выхода 2А, если фотоэффект происходит?
Покажите,пожалуйста,ваши подробные вычисления,а то не получается у меня
Приравняйте 2 равенства и все олучится
Отсюда сразу ответ следует
Задания Д32 C3 № 4653Металлическая пластина облучается светом частотой Гц. Вылетающие из пластины фотоэлектроны попадают в однородное электрическое поле напряжённостью 130 В/м, причём вектор напряжённости поля направлен к пластине перпендикулярно её поверхности. Измерения показали, что на расстоянии 10 см от пластины максимальная кинетическая энергия фотоэлектронов равна 15,9 эВ. Определите работу выхода электронов из данного металла.
Согласно уравнению фотоэффекта, работы выхода фотоэлектронов равна
Направление напряженности электрического поля совпадает с направлением силы, действующей на положительный заряд. Электроны заряжены отрицательно, поэтому поле, направленное перпендикулярно к пластине, будет ускорять электроны. На отрезке длиной x электрическое поле совершит работу по разгону электрона величиной Таким образом, максимальная кинетическая энергия электронов на расстоянии 10 см от пластины равна
Таким образом, работа выхода равна
Задания Д21 № 3622При освещении металлической пластины светом наблюдается фотоэффект. Частоту света плавно изменяют. Установите соответствие между графиками и физическими величинами, зависимости которых от частоты падающего света эти графики могут представлять. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
1) работа выхода фотоэлектрона из металла
2) максимальный импульс фотоэлектронов
3) энергия падающего на металл фотона
4) максимальная кинетическая энергия фотоэлектронов
Энергия фотона прямо пропорциональна частоте: На графике Б изображена именно такая зависимость физической величины от частоты, поэтому этот график соответствует энергии падающего на металл фотона (Б — 3).
Работа выхода фотоэлектрона характеризует свойства материала металлической пластины и не зависит от частоты падающего на нее света, поэтому график этой величины должен представлять собой горизонтальную линию. Максимальный импульс фотоэлектронов связан с с максимальной кинетической энергией соотношением а потому его зависимость от частоты будет нелинейной.
Задания Д21 № 3623При освещении металлической пластины светом наблюдается фотоэффект. Длину волны света плавно изменяют. Установите соответствие между графиками и физическими величинами, зависимости которых от длины волны падающего света эти графики могут представлять. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
2) импульс падающего на металл фотона
3) сила фототока
Работа выхода фотоэлектрона характеризует свойства материала металлической пластины и не зависит от длины волны падающего на нее света, поэтому график этой величины должен представлять собой горизонтальную линию. Тоже самое и для силы фототока: она определяется интенсивностью света, а не его длиной волны. Разберемся с оставшимися вариантами ответа.
Импульс фотона обратно пропорционален длине волны: На графике А изображена именно такая зависимость физической величины от длины волны, поэтому этот график соответствует импульсу падающего на металл фотона (А — 2).
Сила фототока может зависеть от длины волны фотонов тоже. При наличии ускоряющего напряжения доля фотонов (максимальный угол отклонения начальной скорости от направления на анод, при котором электрон еще попадает на анод) зависит от модуля их начальной скорости, и, следовательно, от энергии падающих фотонов.
Рассмотрим уединенный металлический шарик в вакууме, на который падает свет. В этом случае нет ускоряющего напряжения, ни анода с катодом.
Тип 18 № 3641В опыте по изучению фотоэффекта одну из пластин плоского конденсатора облучают светом с энергией фотона 6 эВ. Напряжение между пластинами изменяют с помощью реостата, силу фототока в цепи измеряют амперметром. На графике приведена зависимость фототока I от напряжения U между пластинами. Какова работа выхода электрона с поверхности металла, из которого сделаны пластины конденсатора? (Ответ дать в электрон-вольтах.)
Из графика видно, что фототок пропадает, если подать на пластины конденсатора обратное напряжение в 4 В. Это так называемое запирающее напряжение, когда все вылетающие фотоэлектроны, не успев долететь до противоположной пластины, возвращаются назад под действием электрического поля пластин. Согласно уравнению фотоэффекта Эйнштейна, энергия фотонов связана с работой выхода и запирающим напряжением соотношением: Следовательно, работа выхода для пластины конденсатора равна:
Задания Д21 № 3760Для наблюдения фотоэффекта поверхность некоторого металла облучают светом, частота которого равна Затем частоту света увеличивают вдвое. Как изменятся следующие физические величины: длина волны падающего света, работа выхода электрона, максимальная кинетическая энергия вылетающих электронов?
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться
кинетическая энергия
вылетающих электронов
Длина волны связана с частотой излучения и скоростью света соотношением Следовательно, излучение с вдвое большей частотой имеет вдвое меньшую длину волны.
Работа выхода является характеристикой металла и не зависит от частоты падающего излучения, поэтому работа выхода останется неизменной. Следовательно, увеличение частоты света приведет увеличению максимальной кинетической энергии вылетающих электронов.
Почему длина волны уменьшается? Длина воны=скорость света/частота света. Частота уменьшается, следовательно длина волны увеличивается.
В условии написано: «Затем частоту света увеличивают вдвое».
Тип 19 № 26046Для наблюдения фотоэффекта поверхность некоторого металла облучают светом, частота которого равна Затем частоту света увеличивают вдвое. Как изменятся следующие физические величины: работа выхода электрона и максимальная кинетическая энергия вылетающих электронов?
Тип 18 № 2302Металлическую пластину освещают светом с энергией фотонов 6,2 эВ. Работа выхода для металла пластины равна 2,5 эВ. Какова максимальная кинетическая энергия образовавшихся фотоэлектронов? (Ответ дать в электрон-вольтах.)
Задания Д16 B27 № 2306В таблице приведены значения максимальной кинетической энергии фотоэлектронов при облучении фотокатода монохроматическим светом с длиной волны
Чему равна работа выхода фотоэлектронов с поверхности фотокатода?
Принимая во внимание связь между длиной волны и частотой и используя данные из таблицы, выпишем уравнения фотоэффекта для обоих случаев:
Решая систему этих уравнений, для работы выхода имеем
я вас наверное достала уже ,но не могу понять как здесь получается Е нулевое,запишите вывод формулы подробнее, пожалуйста
Все в порядке, но советую Вам открыть задачник по математике, раздел "системы уравнений", и еще немного потренироваться. Завершающий шаг большинства осмысленных задач по физике — это решение системы уравнений.
Задания Д16 B27 № 2308 Задания Д16 B27 № 2320Работа выхода электронов для исследуемого металла равна 3 эВ. Чему равна максимальная кинетическая энергия фотоэлектронов, вылетающих с поверхности металлической пластинки под действием света, длина волны которого составляет длины волны, соответствующей красной границе фотоэффекта для этого металла?
спасибо за большую помощь в подготовке. в данной задаче длина волны красной границы является минимальной и при последующем уменьшении фотоэффект не имеет место. объясните. пожалуйста.
Частота света и длина волны связаны соотношением .
Для того, чтобы начался фотоэффект, необходимо, чтобы энергия фотона превысила работу выхода. Энергия фотона связана с частотой и длиной волны следующим образом .
Красная граница — это МИНИМАЛЬНАЯ частота или МАКСИМАЛЬНАЯ длина волны, при которой идет фотоэффект
Задания Д16 B27 № 3352Принимая во внимание связь между длиной волны и частотой и используя данные из таблицы, выпишем уравнения фотоэффекта для обоих случаев: Решая систему этих уравнений, для работы выхода имеем
Тип 18 № 6159Работа выхода для некоторого металла равна 3 эВ. На пластинку из этого металла падает свет. На рисунке показана зависимость силы I фототока от приложенного обратного напряжения U. Какова энергия фотона светового излучения, падающего на эту пластинку? (Ответ дать в электрон-вольтах.)
При вылете фотоэлектрона часть энергии фотона затрачивается на преодоление работы выхода металла, а оставшаяся часть уходит на увеличение кинетической энергии электрона При увеличении запирающего напряжения фототок будет уменьшаться, в связи с тем, что кинетической энергии электронов не будет хватать для преодоления электрического поля. Фототок исчезнет, когда потенциальная энергия электронов в электрическом поле станет равной их кинетической энергии Из рисунка видим, что фототок исчезает при напряжении 2 В. Следовательно, максимальная энергия фотоэлектронов 2 эВ. Значит, энергия фотона светового излучения равна 2 + 3 = 5 эВ.
Примеры решения задач
Задача 1. Определите красноволновую границу фотоэффекта для натрия, если работа выхода электрона из фотокатода А=2,3 эВ.
Задача 2. Работа выхода электронов из пластины Авых=6,3 эВ. Определить, произойдет ли внешний фотоэффект, если на пластину падает свет с частотой ν1=8·10 14 Гц, ν2=3·10 16 Гц.
| Дано: | СИ: | Решение: |
| Авых=6,3 эВ | 1·10 -18 Дж | Внешний фотоэлектрический эффект |
| ν1=8·10 14 Гц | произойдет в том случае, если ν>νкр. | |
| ν2=3·10 16 Гц | Уравнение для красной границы фотоэффекта | |
| Найти: | hνкр=Авых (1) | |
| νкр-? | Из (1) определяем νкр=Авых/h. | |
| Вычисления дают νкр=1,5·10 15 Гц | ||
| При этой частоте фотоэффекта не произойдет. | ||
| Во втором случае вычисления покажут, что фотоэффект произойдет. |
Задача 3. При облучении фотоэлемента светом с частотой 1,6·10 15 Гц фототок прекращается при задерживающем напряжении U=4,1 В. Определить А- работу выхода электрона с поверхности фотокатода, λ- красную границу фотоэффекта.
| Дано: | Решение: |
| ν=1,6·10 15 Гц | Электрон может пролететь через тормозящее поле, разность потенциалов которого U, если |
| U=4,1В | eU ≤ (1) |
| h=6,63·10 -34 Дж·с | Уравнение Эйнштейна для фотоэффекта в данном случае имеет вид: |
| е=1,6·10 -19 Кл | е·U=Авых +еU (2), откуда А=hv-еU (3) |
| Найти: | =Авых, откуда λ= |
| Авых-? | A=6,63·10 -34 ·1,6·10 15 -1,6·10 -19 ·4,1=4·10 -19 Дж |
| λкр-? | λ= 5·10 -7 м. |
| Ответ: | А=4·10 -19 Дж, λ=5·10 -7 м. |
Задание 2. Решите количественные задачи.
Задача 1. Длина волны света λ, частота ν, масса фотона mf, импульс Pf, энергия Ef. Определите значение величин, обозначенных «?».
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| λ, нм | ? | ? | 600 | ? | ? | ? | ? | 10 | ? | ? |
| ν, Гц | ? | 5·10 14 | ? | ? | ? | ? | 10 17 | ? | ? | ? |
| mf | mе | ? | ? | ? | ? | mр | ? | ? | ? | ? |
| Pf, | ? | ? | ? | ? | 1,2·10 -27 | ? | ? | ? | ? | 2·10 -30 |
| Ef, Дж | ? | ? | ? | 6,4·10 -19 | ? | ? | ? | ? | 1,5·10 -20 | ? |
Задача 2. Работа выхода электронов с поверхности металла равна Ав. Металл облучается светом с длиной волны λ и частотой ν. Скорость электронов выбитых с поверхности металла . Красная граница λк. Определите значение величин, обозначенных «?».
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ав, эВ | 4,3 | ? | 2,2 | ? | ? | ? | 4,4 | ? | 4 | 3,8 |
| λ , нм | 200 | ? | ? | 250 | ? | 200 | ? | ? | 280 | ? |
| ν , 10 15 Гц | ? | ? | ? | ? | 1,25 | ? | 1,5 | 0,6 | ? | 1 |
| , Мм/с | ? | 0,5 | 1 | ? | ? | ? | ? | ? | ? | ? |
| λк , нм | ? | 280 | ? | 309 | 326 | 288 | ? | 563 | ? | ? |
Задача 3. Задерживающая разность потенциалов в опыте по фотоэффекту равна Uз. Скорость фотоэлектронов , энергия - E. Определите значение величин, обозначенных «?».
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Uз, В | 3 | ? | ? | 9 | ? | ? | 4 | ? | ? | 5 |
| , Мм/с | ? | 1,8 | ? | ? | 3 | ? | ? | 1,2 | ? | ? |
| E,10 -19 Дж | ? | ? | 6,4 | ? | ? | 10 | ? | ? | 3,2 | ? |
Задача 4. Работа выхода электронов с поверхности металла Ав, задерживающая разность потенциалов Uз, частота падающего света ν, масса фотонов mf. Определите значение величин, обозначенных «?».
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ав, эВ | 4 | ? | 4,4 | ? | 4,3 | 4 | ? | ? | 3,8 | ? |
| Uз, В | 3,2 | 4,5 | ? | 6 | ? | 5,3 | 2,8 | 4,4 | ? | 5 |
| ν,10 15 Гц | ? | ? | 1,5 | 2,4 | 2,17 | ? | ? | 2,1 | 1,75 | ? |
| mf,10 -35 кг | ? | 1,17 | ? | ? | ? | ? | 0,9 | ? | ? | 1,5 |
Задача 5. При торможении электронов, проходящих разность потенциалов Uобразуется рентгеновское излучение с частотой ν, и длиной волны λ. Определите значение величин, обозначенных «?».
Читайте также:
