Металлическая пластина в конденсаторе
Электрическая емкость — последняя тема главы «Электростатика». При решении задач на эту тему могут потребоваться все сведения, полученные при изучении электростатики: сохранение электрического заряда, понятия напряженности поля и потенциала, поведение проводников в электростатическом поле, изменение напряженности поля в диэлектриках, закон сохранения энергии применительно к электростатическим явлениям. Только при хорошем усвоении всех основных понятий электростатики решение задач на электрическую емкость не вызовет особых затруднений.
Основными формулами при решении задач на емкость являются следующие: формула (1.24.2) — определение емкости, формула (1.24.3) — емкость уединенного шара, выражения для емкости плоского конденсатора (1.25.3) и сферического конденсатора (1.25.7), а также формулы для определения емкости батареи конденсаторов при последовательном и параллельном их соединении (1.26.4) и (1.26.2).
Надо знать еще формулы (1.27.3) и (1.27.9) для энергии заряженного конденсатора и заряженного уединенного тела.
Задача 1
Два одинаковых металлических шарика радиусом г расположены в вакууме на расстоянии d друг от друга, причем d >> r. Шарики заряжены одинаковыми по модулю и противоположными по знаку зарядами. Какова электрическая емкость системы, образованной шариками?
Решение. Искомая емкость равна отношению заряда q одного из шариков к разности потенциалов между ними:
Найдем U. Потенциал φ1 первого шарика, несущего заряд +q, складывается из его собственного потенциала : (см. задачу 16 § 1.23).

Аналогично потенциал второго шарика

Отсюда разность потенциалов

Поскольку d >> r, то с большой степенью точности можно считать, что
Задача 2
Найдите емкость С конденсатора, площадь пластин которого S и расстояние между ними l, если в конденсатор вставлена металлическая пластина толщиной d, параллельная его обкладкам (рис. 1.107).

Решение. Конденсатор со вставленной в него пластиной можно рассматривать как два последовательно соединенных конденсатора. Емкость первого из них . При последовательном соединении электрическая емкость батареи определяется уравнением:

Емкость не зависит от положения пластины. При очень тонкой пластине (d ⇒ 0) емкость конденсатора не зависит от наличия пластины.
Задача 3
В плоский конденсатор с расстоянием d между обкладками вводится диэлектрическая пластина, толщина которой d1 < d.
Определите емкость конденсатора с диэлектрической пластиной. Диэлектрическая проницаемость материала пластины ε. Площадь пластины и каждой обкладки конденсатора S.
Решение. Если в плоский конденсатор внести очень тонкую проводящую пластину, параллельную обкладкам, то на ее поверхностях появятся заряды противоположных знаков, равные по модулю. При этом емкость конденсатора не изменяется (см. задачу 2). Поэтому можно считать, что на поверхностях диэлектрической пластины нанесены тонкие проводящие слои. В этом случае образуются три последовательно соединенных конденсатора с емкостями

где d2 и d3 — расстояния между поверхностями диэлектрической пластины и обкладками, причем d2 + d2 = d - d1 (рис. 1.108).

Емкость С батареи из трех конденсаторов определяется из формулы


Задача 4
Ha рисунке 1.109 изображена батарея конденсаторов. Их емкости равны С1 = C, C2 = 2С, C3 = ЗС, С4 = 6С. Изменится ли емкость батареи, если между точками А и В включить конденсатор с емкостью C5 = 8С?

Решение. Обозначим потенциалы на зажимах батареи φ1 и φ2, а в точках А и В соответственно φ3 и φ4.
Так как конденсаторы С1 и СЗ соединены последовательно, то их заряды одинаковы, т.е.


Разделив почленно равенство (1.28.1) на равенство (1.28.2) и учитывая, что, согласно условию задачи,

Отсюда найдем, что φ3 = φ4. т. е. точки А и В имеют одинаковые потенциалы. Поэтому если включить какой-либо конденсатор между точками А и В (рис. 1.110), то он не зарядится и, следовательно, не повлияет на емкость системы.


Схема, подобная схеме, изображенной на рисунке 1.110, называется мостовой. Конденсаторы С1 и С2, СЗ и С4 называются плечами моста. Обратите внимание, что если емкости плеч моста пропорциональны , то точки А и В имеют одинаковые потенциалы. Конденсатор С5 не заряжается, и его из схемы можно удалить (см. рис. 1.109).
Задача 5
Найдите емкость батареи конденсаторов, изображенной на рисунке 1.111. Емкость каждого конденсатора равна С.

Решение. Данная схема соединения конденсаторов эквивалентна схеме, изображенной на рисунке 1.112. В этом можно убедиться, проверив, что каждый из конденсаторов соединен с источником и с другими конденсаторами точно так же, как в исходной схеме.

Вследствие равенства емкостей всех конденсаторов разность потенциалов между точками А и В равна нулю. Поэтому конденсатор 4 можно исключить (см. задачу 4). В результате получится схема, изображенная на рисунке 1.113. Она состоит из трех параллельных ветвей, две из которых содержат по два последовательно включенных конденсатора.

Общая емкость системы

Задача 6
Два маленьких шарика радиусом г несут заряды q1 и q2, различные по модулю, но одинаковые по знаку. Шарики первоначально находятся на расстоянии l друг от друга. Один из шариков закреплен. Второй шарик, удаляясь под действием электростатических сил, приобретает максимальную кинетическую энергию Wk1. Если перед началом движения второго шарика оба шарика на некоторое время были соединены проводником, то второй шарик, удаляясь, приобретает максимальную кинетическую энергию Wk2 > Wk1. Определите количество теплоты, выделившееся в проводнике при соединении шариков, и выясните, за счет какой энергии выделяется эта теплота и увеличивается кинетическая энергия второго шарика.
Решение. Согласно закрну сохранения энергии в первом случае

где Wk01 и Wp01 + W0c — начальные, a Wk1 и Wp1 + W1c — конечные значения кинетической и потенциальной энергий системы двух шариков. Причем Wp01 и W1c, — потенциальные энергии взаимодействия шариков, а W0c и W1c — их суммарные собственные энергии, одинаковые по модулю. Считая потенциальную энергию взаимодействия при бесконечно большом расстоянии между шариками равной нулю и учитывая, что Wk01 = 0, получим:


Нетрудно видеть, что действительно Wk2 > Wk1. Кроме того, в проводнике выделяется количество теплоты Q. Однако, разумеется, полная энергия должна сохраняться. Увеличение кинетической энергии и выделение теплоты во втором случае происходит за счет уменьшения собственной потенциальной энергии заряженных шариков при их соединении.
С учетом собственной энергии шариков конечную энергию в первом случае можно представить в виде

— собственная энергия шариков. Конечную энергию во втором случае запишем так:


Количество выделенной теплоты равно:
Упражнение 4
1. Пластины заряженного конденсатора попеременно заземляются. Будет ли при этом конденсатор разряжаться?
2. Плоский конденсатор, расстояние между обкладками которого d1 = 10 мм, зарядили до разности потенциалов U1 = 100 В, а затем отключили от сети. Определите разность потенциалов U2 между обкладками конденсатора, если их раздвинули до расстояния d2 = 20 мм.
3. Определите емкость конденсатора, площадь пластин которого равна S, а расстояние между пластинами d, если пластины погружены вертикально в жидкий диэлектрик до середины. Диэлектрическая проницаемость диэлектрика равна е.
4. В конденсатор емкостью C0 внесли диэлектрическую пластинку с диэлектрической проницаемостью ε = 2. Пластинку расположили так, как указано на рисунке 1.114. Определите, во сколько раз изменилась емкость конденсатора при внесении в него пластинки. Площадь пластинки в 2 раза меньше площади обкладки конденсатора, а ее толщина в 2 раза меньше расстояния между обкладками.

5. Плоский конденсатор, пространство между пластинами которого заполнено керосином (ε = 2), расположен вертикально, заряжен и отключен от источника напряжения. Напряженность электрического поля при этом в керосине Е = 20 кВ/см. Из-за дефекта в корпусе конденсатора керосин начинает вытекать, а его место занимает воздух. Предельная напряженность электрического поля в воздухе, при которой наступает электрический пробой (разряд), Епр = 30 кВ/см. Какая доля δ керосина вытечет из конденсатора к моменту пробоя конденсатора?
6. Оцените приближенно электрическую емкость тела человека.
7. Найдите емкость металлического шара радиусом r, окруженного прилегающим концентрическим слоем диэлектрика с внешним радиусом R и диэлектрической проницаемостью ε.
8. К пластинам плоского конденсатора, находящимся на расстоянии d = 1 см друг от друга, приложена разность потенциалов U = 300 В. В пространство между пластинами помещается плоскопараллельная пластина из стекла толщиной d1 = 0,3 см и плоскопараллельная пластина из парафина толщиной d2 = 0,7 см. Найдите напряжения между поверхностями стеклянной и парафиновой пластин. Диэлектрические проницаемости стекла и парафина соответственно равны ε1 = б и ε2 = 2,6.
9. Определите емкость конденсатора с трехслойным диэлектриком, диэлектрические проницаемости слоев равны ε1, ε2, ε1 (рис. 1.115). Толщина каждого диэлектрика (слоя) равна d. Площадь пластин S.

10. Четыре одинаковые металлические пластины расположены в воздухе на равных расстояниях d друг от друга (d мало по сравнению с размерами пластин). Площадь каждой из пластин равна S. Пластина 1 соединена проводником с пластиной 3, а от пластин 2 и 4 сделаны выводы (рис. 1.116). Определите емкость С такого конденсатора.

11. Определите емкость С батареи конденсаторов, схематически изображенной на рисунке 1.117. У каждого конденсатора указано значение его емкости, выраженное в микрофарадах.

12. Из проволоки сделан куб, в каждое ребро которого включено по одному конденсатору емкостью С (рис. 1.118). Найдите емкость получившейся батареи конденсаторов, если она включается в цепь проводниками, присоединенными к вершинам А и В куба.

13. Имеется N точек в пространстве. Между каждой парой точек включен конденсатор емкостью С. Найдите емкость образовавшейся батареи конденсаторов, если она включается в цепь выводами, присоединенными к двум произвольным точкам.
14. Плоский конденсатор емкостью С = 15 пФ зарядили до разности потенциалов U = 100 В, затем отключили от источника и погрузили полностью в жидкий диэлектрик (ε = 1,5). Определите изменение энергии конденсатора ΔWp.
15. Три конденсатора емкостью С = 1 мкФ каждый соединены последовательно. Конденсаторы зарядили и отключили от источника. Заряд этой батареи q = 10 -4 Кл. Затем пространство между обкладками одного из конденсаторов заполнили диэлектриком с диэлектрической проницаемостью ε = 2. Найдите энергию, запасенную в электрическом поле этих конденсаторов, и напряжение на зажимах батареи после заполнения диэлектриком одного из конденсаторов.
16. Энергия заряженного плоского конденсатора, заполненного диэлектриком, равна Wp = 2 • 10 -5 Дж. После отключения конденсатора от источника напряжения диэлектрик из конденсатора вынули, совершив при этом работу А = 7 • 10 -5 Дж. Найдите диэлектрическую проницаемость диэлектрика.
17. Сделаем в пластинах плоского конденсатора два малых отверстия — одно напротив другого. Пусть через одно из отверстий в заряженный конденсатор влетает с небольшой начальной скоростью частица так, чтобы электрическое поле конденсатора ускоряло ее (рис. 1.119).

Пролетев через конденсатор, частица вылетает из другого отверстия, приобретая дополнительную энергию ΔWp = qU, где q — заряд частицы, а U — разность потенциалов на пластинах конденсатора. Теперь с помощью магнитного поля направление движения частицы изменяется таким образом, чтобы она снова влетела через первое отверстие в конденсатор (см. рис. 1.119). (В главе 4 вы узнаете, что сила, действующая со стороны магнитного поля на движущуюся заряженную частицу, не совершает работы.) При повторном пролете через конденсатор частица вновь приобретает дополнительную энергию ΔWp, в следующем цикле — еще ΔWp и т. д. Получается циклический ускоритель, который не нуждается в источнике энергии! Где ошибка в приведенных рассуждениях?
18. Два конденсатора емкостью С1 и C2 заряжены до разности потенциалов U1 и U2 (U1 ≠ U2). Докажите, что при параллельном соединении этих конденсаторов их общая энергия уменьшается. Объясните, почему происходит уменьшение энергии.
19. Две прямоугольные пластины длиной l и площадью S расположены параллельно друг другу на расстоянии d (плоский конденсатор). Пластины заряжены до разности потенциалов U. В пространство между пластинами втягивается диэлектрик с диэлектрической проницаемостью ε. Толщина диэлектрика равна d, его ширина равна ширине пластин, а длина больше l (рис. 1.120). Трение отсутствует. Найдите зависимость силы, действующей на диэлектрик со стороны поля, от расстояния х.

20. Решите задачу 19 при условии, что разность потенциалов между пластинами поддерживается постоянной и равной U.
Мы потратили довольно много времени на изучение электричества, а рассмотрели лишь простейший частный случай неподвижных заряженных тел — электростатику. Может быть, не стоило уделять электростатике такое больпюе внимание? Нет, стоило! Мы ввели важнейшие понятия, используемые во всей электродинамике: «электрический заряд», «электрическое поле», «потенциал» и «разность потенциалов», «электрическая емкость», «энергия электрического поля». На простом частном случае выяснить суть этих фундаментальных понятий не так трудно, как в общем случае движущихся зарядов.
Теперь перейдем к изучению электромагнитных процессов, наблюдаемых при движении заряженных частиц.
Металлическая пластина в конденсаторе
Тип 16 № 3130Плоский конденсатор отключили от источника тока, а затем уменьшили расстояние между его пластинами. Как изменили при этом заряд на обкладках конденсатора, электроемкость конденсатора и напряжение на его обкладках? (Краевыми эффектами пренебречь, считая пластины конденсатора большими. Диэлектрическую проницаемость воздуха принять равной 1.)
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Заряд конденсатора | Электроёмкость | Напряжение на обкладках |
Поскольку конденсатор отключен от источника, при изменении расстояния между пластинами заряд конденсатора никак не изменяется. Электроемкость плоского конденсатора обратно пропорциональна расстоянию между пластинами: Следовательно, уменьшение расстояния между обкладками конденсатора приводит к увеличению его электроемкости. Наконец, напряжение на обкладках связано с зарядом конденсатора и его емкостью соотношением Таким образом, напряжение уменьшается.
Тип 16 № 3516Между пластинами заряженного плоского конденсатора поместили диэлектрик с диэлектрической проницаемостью так, что он полностью заполнил объем между пластинами. Как изменились емкость конденсатора, заряд на пластинах и напряжение между ними, если конденсатор подключен к источнику?
А) Заряд на пластинах
Б) Напряжение между пластинами
В) Емкость конденсатора
1) Уменьшится в раз
2) Останется неизменной
3) Увеличится в раз
К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Поскольку конденсатор подключен к источнику, напряжение между пластинами конденсатора равно напряжению источника, а значит, постоянно (Б — 2). Ёмкость плоского конденсатора пропорциональна диэлектрической проницаемости диэлектрика внутри него: Следовательно, введение диэлектрика приводит к увеличению ёмкости конденсатора в раз (В — 3). Наконец, заряд на пластинах конденсатора связан с его ёмкостью и напряжением на нём соотношением: Таким образом, после введения диэлектрика заряд конденсатора увеличится в раз (А — 3).
Заряд не может измениться. Изменится напряжение.
Конденсатор подключён к источнику.
А где в задании сказано что он подключён к источнику тока? В задании указанно лишь то что конденсатор заряжен. По моему ошибка в задании, поправьте если не прав.
В условии написано: «Как изменились (. ), если конденсатор подключен к источнику?»
Тип 16 № 4212Пластины плоского конденсатора, подключённого к батарее, сделаны из металлических листов в виде квадрата со стороной а. Квадратные пластины заменили на круглые диаметром а. При этом расстояние между пластинами увеличили, а батарею оставили прежней. Как в результате изменятся следующие физические величины: электрическая ёмкость конденсатора, модуль напряжённости электрического поля между пластинами конденсатора, заряд конденсатора?
A) Электрическая ёмкость конденсатора
Б) Модуль напряжённости электрического поля между пластинами конденсатора
B) Заряд конденсатора
Ёмкость плоского конденсатора связана с площадью его пластин и расстоянием между ними следующим образом: При замене квадратных пластин на круглые, площадь пластин уменьшается, так как круг диаметра a вписывается в квадрат со стороной Таким образом, в результате замены пластин и увеличении расстояния между ними, ёмкость конденсатора уменьшается (А — 2).
Модуль напряжённости электрического поля между пластинами конденсатора связан с расстоянием между ними и напряжением на них соотношением: Поскольку источник остался прежний, увеличение расстояния между пластинами приводит к уменьшению модуля напряжённости (Б — 2).
Наконец, заряд конденсатора связан с напряжением на нём и ёмкостью через Как уже было установлено, емкость уменьшается, значит, уменьшается и заряд (В — 2).
Тип 16 № 3515Между пластинами заряженного плоского конденсатора поместили диэлектрик с диэлектрической проницаемостью так, что он полностью заполнил объем между пластинами. Как изменились емкость конденсатора, заряд на пластинах и напряжение между ними, если конденсатор отключен от источника?
Поскольку конденсатор отключен от источника, заряд на его пластинах меняться не может, ему просто некуда деться и не от куда взяться (А — 2). Емкость плоского конденсатора пропорциональна диэлектрической проницаемости диэлектрика внутри него: Следовательно, введение диэлектрика приводит к увеличению емкости конденсатора в раз (В — 3). Наконец, напряжение между пластинами конденсатора связано с его емкостью и зарядом конденсатора соотношением: Таким образом, после введения диэлектрика напряжением уменьшится в раз (Б — 1).
Тип 16 № 6898Плоский конденсатор с воздушным зазором между обкладками подключён к источнику постоянного напряжения. Как изменятся величина заряда конденсатора и разность потенциалов между его обкладками при увеличении зазора между ними?
Электроемкость плоского конденсатора обратно пропорциональна расстоянию между его пластинами: Таким образом, при увеличении расстояния между обкладками емкость конденсатора уменьшится.
Также Так как конденсатор подключен к источнику постоянного напряжения, разность потенциалов остается неизменной. А между емкостью конденсатора и величиной заряда прямая пропорциональность, значит, заряд конденсатора уменьшится.
Тип 24 № 7873Воспользовавшись оборудованием, представленным на рис. 1, учитель собрал модель плоского конденсатора (рис. 2), зарядил нижнюю пластину положительным зарядом, а корпус электрометра заземлил. Соединённая с корпусом электрометра верхняя пластина конденсатора приобрела отрицательный заряд, равный по модулю заряду нижней пластины. После этого учитель сместил одну пластину относительно другой не изменяя расстояния между ними (рис. 3). Как изменились при этом показания электрометра (увеличились, уменьшились, остались прежними)? Ответ поясните, указав, какие явления и закономерности вы использовали для объяснения. Показания электрометра в данном опыте прямо пропорциональны разности потенциалов между пластинами конденсатора.
Коль скоро показания электрометра прямо пропорциональны разности потенциалов между пластинами конденсатора, рассмотрим связь разности потенциалов с зарядом и ёмкостью конденсатора: Ёмкость плоского конденсатора равна Поскольку расстояние между пластинами d и диэлектрическая проницаемость воздуха не изменились, а перекрываемая площадь пластин S уменьшилась, то и ёмкость конденсатора уменьшилась. Заряд на пластиках остался неизменным, ему некуда утечь. Значит, разность потенциалов возросла. Показания электрометра увеличились.
§ 54. Конденсатор
Как вам известно, вокруг заряженных тел существует электрическое поле, которое обладает энергией.
А можно ли накапливать заряды и энергию электрического поля? Устройством, позволяющим накапливать заряды, является конденсатор (от лат. condensare — сгущение). Простейший плоский конденсатор состоит из двух одинаковых металлических пластин — обкладок, находящихся на небольшом расстоянии друг от друга и разделённых слоем диэлектрика, например воздуха (рис. 83). Толщина диэлектрика в сравнении с размерами обкладок небольшая.

Рис. 83. Простейший конденсатор и его обозначение на схеме
Продемонстрируем на опыте способность конденсатора накапливать заряды. Для этого две металлические пластины подключим к разным полюсам электрофорной машины (рис. 84). Пластины получат одинаковые по модулю, но разные по знаку заряды. Возникнет электрическое поле. Электрическое поле конденсатора практически сосредоточено между пластинами внутри конденсатора.

Рис. 84. Зарядка конденсатора от электро-форной машины
После отключения электрофорной машины заряды на пластинах и электрическое поле между ними сохранятся.
Если обкладки заряженного конденсатора соединить проводником, то по проводнику некоторое время будет проходить ток. Значит, заряженный конденсатор является источником тока.
В зависимости от диэлектрика конденсаторы бывают нескольких типов: с твёрдым, жидким и газообразным диэлектриком. Их различают и по форме обкладок: плоские, цилиндрические, сферические и др. (рис. 85).

Рис. 85. Различные типы конденсаторов
Свойство конденсатора накапливать электрические заряды характеризуется электроёмкостью, или ёмкостью. Для того чтобы понять, от чего зависит эта физическая величина, обратимся к опыту.
Две металлические пластины, укреплённые на изолирующих подставках параллельно друг другу, соединим с электрометром. Одну из пластин соединим со стержнем электрометра, другую заземлим, соединив с корпусом прибора (рис. 86, а). Наэлектризованным шаром коснёмся внешней стороны пластины А, тем самым сообщив ей положительный заряд +q. Под действием электрического поля пластины А в пластине В произойдёт перераспределение зарядов: отрицательные заряды расположатся на внутренней стороне пластины. С земли придут свободные электроны, чтобы нейтрализовать положительные заряды на внешней стороне пластины В. Таким образом, на пластине В возникнет равный по величине отрицательный заряд -q.

Рис. 86. Зависимость ёмкости конденсатора от площади, расстояния между пластинами, диэлектрика между пластинами
Стрелка электрометра отклонится от нулевого положения. С помощью одинаково заряженных шаров продолжим передавать конденсатору заряды последовательно равными порциями. Мы заметим, что при увеличении заряда в 2, 3, 4 раза соответственно в 2, 3, 4 раза увеличатся показания электрометра, т. е. увеличится напряжение между пластинами конденсатора. Причём отношение заряда к напряжению будет оставаться постоянным:
Электроёмкость конденсатора вычисляется по формуле:
1 Ф — это очень большая ёмкость, поэтому на практике используют микрофарад (мкФ) и пикофарад (пФ).
1 мкФ = 10 -6 Ф; 1 пФ = 10 -12 Ф.
Выясним, от чего зависит ёмкость кондесатора. Для этого возьмём конденсатор с пластинами, имеющими большую площадь (рис. 86, б). Повторим опыт. Отношение заряда к напряжению и в этом случае остаётся постоянным
но отношение заряда к напряжению теперь больше, чем в первом опыте, т. е. С1 > С. Чем больше площадь пластин, тем больше ёмкость конденсатора.
Ещё раз проделаем первый опыт, но теперь изменим расстояние между пластинами (рис. 86, в). С уменьшением расстояния между пластинами уменьшается напряжение между ними. При уменьшении расстояния между пластинами конденсатора при неизменном заряде ёмкость конденсатора увеличивается.
Проделаем ещё один опыт. Установим пластины конденсатора А и В на некотором расстоянии друг от друга. Пластину А зарядим. Заметим показания электрометра, когда между пластинами находится воздух. Разместим между пластинами лист из оргстекла или другой диэлектрик (рис. 86, г). Мы заметим, что напряжение между пластинами уменьшится. Следовательно, ёмкость конденсатора зависит от свойств внесённого диэлектрика.
При внесении диэлектрика ёмкость конденсатора увеличивается.
Конденсатор, как и любое заряженное тело, обладает энергией. Проверим это на опыте. Зарядим конденсатор и подсоединим к нему электрическую лампочку. Лампочка ярко вспыхнет. Это свидетельствует о том, что заряженный конденсатор обладает энергией. Энергия конденсатора превращается во внутреннюю энергию нити накаливания лампы и проводов. Для того чтобы зарядить конденсатор, нужно было совершить работу по разделению положительных и отрицательных зарядов. В соответствии с законом сохранения энергии, совершённая работа А равна энергии конденсатора Е, т. е.
где Е — энергия конденсатора.
Работу, которую совершает электрическое поле конденсатора, можно найти по формуле:
где Uср — это среднее значение напряжения.
Поскольку в процессе разрядки напряжение не остаётся постоянным, необходимо найти среднее значение напряжения:
Uср = U/2; тогда А = qUср = qU/2,
так как q = CU, то А = CU 2 /2.
Значит, энергия конденсатора ёмкостью С будет равна:
Конденсаторы могут длительное время накапливать энергию, а при разрядке они отдают её почти мгновенно. Свойство конденсатора накапливать и быстро отдавать электрическую энергию широко используется в электротехнических и электронных устройствах, в медицинской технике (рентгеновская техника, устройства электротерапии), при изготовлении дозиметров, аэрофотосъёмке.
Вся правда о конденсаторах: волшебные свойства загадочных баночек
Было ли лучшее время для энтузиастов и любителей Hi-Fi, чем конец 1970-х и начало 1980-х годов? С одной стороны, так много всего происходило с развитием цифрового аудио, а с другой — наблюдался рост субъективизма. Внезапно проигрыватели и усилители стали оценивать не по уровню детонации, выходной мощности и гармоническим искажениям, а по их звучанию! И можно было даже всерьёз говорить о звучании кабелей. В этой новой атмосфере всё, что когда-то считалось само собой разумеющимся в области Hi-Fi, стало кандидатом на переоценку.

Пристальному изучению подверглось и влияние на звук пассивных электронных компонентов — резисторов, индуктивностей и конденсаторов. В особенности, конденсаторов. Знающие люди начали обсуждать такие явления как эквивалентное последовательное сопротивление (ESR) и диэлектрическое поглощение.
Сегодня мы нечасто слышим об этой теме, но не потому, что проблема была исчерпана. Скорее всего, разработчики нынче уделяют столь же пристальное внимание используемым пассивным компонентам, как и схемам, в которых они применяются, так что общественный фурор несколько стих.

В простейшем виде конденсатор состоит из двух металлических пластин, разделённых воздухом (или, ещё лучше, вакуумом) и схематично изображён на рис. 1. Поскольку между пластинами нет проводящего пути, конденсатор блокирует постоянный ток (например, от батареи). При этом конденсатор, напротив, пропускает сигналы переменного тока — как раз такие как звуковые волны.
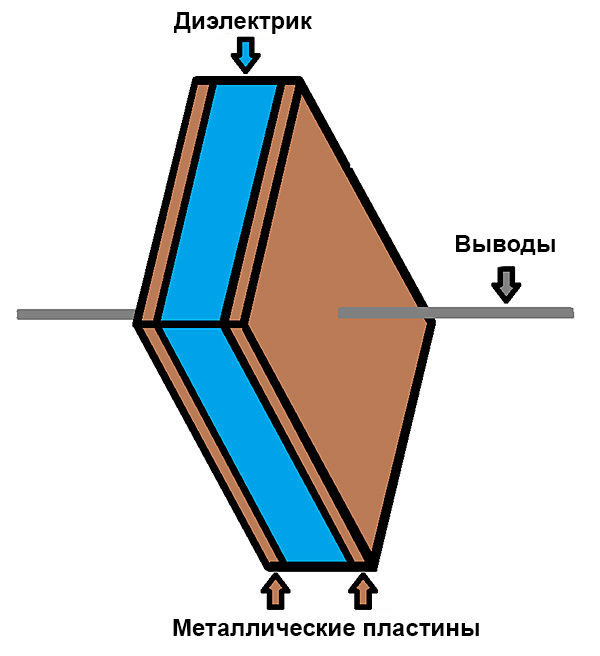
Рис. 1. Компоненты, из которых состоит конденсатор — две проводящие пластины, разделённые слоем диэлектрика.
Проверенное решение
Мы нечасто сталкиваемся с воздушными конденсаторами, но если вы заглядывали внутрь старого лампового радиоприемника и видели элемент, отвечающий за настройку, который состоит из чередующихся металлических пластин, это как раз воздушный конденсатор переменной ёмкости. В большинстве конденсаторов, с которыми мы сталкиваемся в аудиотехнике и прочей электронике, в качестве изолирующего материала (диэлектрика), разделяющего пластины, не используется воздух, поскольку он имеет низкую диэлектрическую постоянную (1,0), а это означает, что воздушные конденсаторы большой емкости слишком громоздкие, чтобы быть практичными. По этой причине используются, в основном, твёрдые диэлектрики, с более высокими диэлектрическими свойствами, в том числе из керамики и различных видов пластмасс (например, ПВХ с диэлектрической проницаемостью 4,0). Именно здесь история становится особенно интересной, поскольку для всех этих диэлектриков характерны те или иные компромиссы в плане влияния на звук, в то время как воздух практически идеален.
Простые фильтры
Для начала, узнаем побольше о том, как ведут себя конденсаторы и для чего они используются. Конденсаторы блокируют постоянный ток и пропускают переменный, однако они не пропускают переменный ток с разной частотой одинаково. Это объясняется тем, что конденсаторы обладают реактивным сопротивлением, которое снижается с увеличением частоты (к слову, катушки индуктивности тоже обладают реактивным сопротивлением, которое, наоборот, увеличивается с ростом частоты).

Таким образом, конденсаторы пропускают высокочастотные сигналы легче, чем низкочастотные, что делает их крайне полезными в частотно-селективных цепях (то есть, в фильтрах), а также для устранения нежелательных сигналов (например, гул или шум с шины питания постоянного напряжения).
Простые фильтры верхних и нижних частот показаны на рис.2. В фильтре верхних частот (рис. 2а) последовательно включенный конденсатор подключен к шунтирующему резистору. В фильтре нижних частот (рис. 2b) конденсатор и резистор меняются местами.

Рис. 2. RC-фильтр первого порядка верхних (2a) и нижних (2b) частот.
Итак, конденсаторы зачастую используются для объединения цепей, отделения нежелательного шума в цепях постоянного напряжения и в частотно-селективных цепях (фильтрах). Поскольку конденсаторы накапливают электрический заряд, большие из них также применяются в качестве резервуаров в источниках питания переменного и постоянного тока. На рис. 3 показан типовой источник питания, включающий в себя понижающий трансформатор (он понижает напряжение сети), мостовой выпрямитель (который преобразует переменный ток из трансформатора в импульсный постоянный ток) и пару конденсаторов-резервуаров (сглаживающих пульсации после выпрямления переменного тока).

Рис.3. Принципиальная схема двухполупериодного источника питания, состоящего из понижающего трансформатора, двухполупериодного мостового выпрямителя и двух резервуарных конденсаторов.
Подобные схемы встречаются во многих твердотельных аудиокомпонентах. Аналогичные решения используются и в ламповом оборудовании, но из-за высоких напряжений, требуемых для работы ламп, трансформатор здесь обычно повышает напряжение сети.
Ёмкость резервуарных конденсаторов, используемых в транзисторных усилителях мощности, может достигать 50 000 мкФ и более, тогда как в других случаях в схеме могут использоваться конденсаторы емкостью 1 НФ (одна тысячная микрофарада) или даже меньше. Таким образом, очевидно, что некоторые типы конденсаторов лучше подходят под определённые задачи, чем другие.
Важное уточнение
Как правило, самые большие резервуарные конденсаторы являются электролитическими, ведь они обеспечивают высокую ёмкость в сравнительно небольшом объёме. Такие конденсаторы содержат электролит (жидкость или гель), который химически реагирует с металлической фольгой внутри банки, образуя слой диэлектрика. Подобные электролитические конденсаторы, а также некоторые другие — например, танталовые, называются полярными, а несоблюдение полярности подключения может привести к их выходу из строя.
Другая разновидность — неполярные конденсаторы, которые можно подключать без учёта полярности. Подобные электролиты иногда использовались в пассивных кроссоверах акустических систем, однако такая практика сегодня устарела, поскольку плёночные конденсаторы справляются с этой задачей лучше, хоть и занимают больше места.
Конденсаторы также могут иметь различное расположение выводов — аксиальное (осевое) или радиальное. Преимущество радиальных электролитов заключается в том, что они занимают меньше площади на плате, однако их минус — в том, что они увеличивают её высоту. В больших электролитических конденсаторах обычно отказываются от выводов под пайку — в пользу винтовых клемм.
Что скрывают конденсаторы
Настоящие конденсаторы, как и настоящие политики, ведут себя не идеально, и именно здесь кроется причина их влияния на качество звука. Во-первых, на практике ни один конденсатор не является только ёмкостью — он также имеет индуктивность и сопротивление. На принципиальной схеме конденсатор обычно обозначается одним из символов на рис. 4 (все они визуально отсылают к двум разделенным пластинам), однако в реальности он представляет собой что-то вроде схемы, представленной на рис. 5. Резистор обозначенный на рисунке как ESR (эквивалентное последовательное сопротивление) может быть не постоянным — сопротивление может зависеть от частоты. В случае с электролитическими конденсаторами, ESR обычно уменьшается с частотой.

Рис. 4. Варианты обозначения конденсаторов на схеме
Одним из последствий того, что у конденсаторов есть индуктивность (ESL или эквивалентная последовательная индуктивность на рис. 6), является то, что они, по сути, являются электрически резонансными. Если проанализировать импеданс конденсатора в зависимости от частоты, он не будет продолжать уменьшаться с ростом частоты. На рис. 6 показано, что импеданс достигает минимума (эквивалентного значению ESR) на резонансной частоте, а затем, по мере увеличения частоты, он снова начинает расти из-за ESL.
Рис. 5. Схематичный эквивалент реального конденсатора демонстрирует паразитное сопротивление (ESR) и индуктивность (ESL) Рис. 6. Паразитная индуктивность приводит к тому, что у конденсаторы имеют электрический резонанс, иногда — в пределах слышимого диапазона частот.
У больших электролитических конденсаторов частоты электрического резонанса обычно находятся в пределах звукового диапазона. У небольших конденсаторов частоты электрического резонанса могут превышать 1 МГц. Для увеличения частоты электрического резонанса для заданной емкости следует уменьшить ESL — последовательную индуктивность.
Для достижения этой цели, при разработке электролитических конденсаторов, где такая проблема стоит наиболее остро, применяются различные методы. Например, в конденсаторах DNM T-Network для снижения индуктивности используются специальные Т-образные соединения из фольги — таким образом, их резонансная частота более чем в два раза выше по сравнению со стандартной конструкцией (от 28 кГц до 75 кГц — в примере, который приводит компания DNM на своём веб-сайте).

ESR оказывает потенциально благотворное влияние на демпфирование электрического резонанса конденсатора, однако, в отличие от индуктивности или ёмкости, сопротивление генерирует тепло в то время, когда через конденсатор проходит ток. В больших ёмкостных конденсаторах, где проходящие через них токи велики, этот эффект внутреннего нагрева ограничивает безопасные условия эксплуатации. Тем не менее, электролитические конденсаторы лучше всего работают именно тёплыми.
Микрофонный эффект
Не секрет, что ламповое оборудование чувствительно к вибрации. Внутри вакуумированной стеклянной оболочки лампы находятся тонкие металлические электроды, расстояние между которыми влияет на работу лампы. Таким образом, если встряхнуть лампу достаточно сильно, это отразится на её электрической мощности — эффект, который называют «микрофонным», поскольку лампа в таком случае ведёт себя подобно микрофону.
Твердотельная электроника меньше подвержена этому эффекту, однако приведём в пример некий крайний случай: разработчики первых систем управления двигателем в гоночных автомобилях вскоре научились не прикреплять электронные блоки к двигателю, либо использовать хорошую изоляцию, иначе вибрации от двигателя могли нарушить её работу. Уровни вибрации, которые испытывает Hi-Fi оборудование при повседневном использовании, гораздо ниже, однако некоторые производители, среди которых, например, Naim Audio, по-прежнему прилагают большие усилия, чтобы свести к минимуму вероятное воздействие микрофонного эффекта.
Способность конденсатора накапливать заряд (его ёмкость) пропорциональна площади пластин и обратно пропорциональна расстоянию между ними, а «пластины» обычно представляют собой тонкую фольгу с тонкими слоями диэлектрика между ними. Это приводит к тому, что конденсаторы подвержены воздействию микрофонного эффекта, поскольку из-за вибрации расстояние между пластинами и, следовательно, значение ёмкости может меняться.
Таким образом, физические свойства материалов, из которых изготовлен конденсатор, могут быть столь же важны, как и электрические параметры. Но что ещё интереснее, вибрация извне не является необходимым условием для того, чтобы конденсаторы страдали от её воздействия, ведь силы, формируемые напряжениями и токами внутри самого конденсатора, также могут вызывать механические резонансы. Из-за этого эффекта можно даже услышать, как некоторые конденсаторы издают звук, когда через них проходит сигнал. В кроссовере акустической системы, где уровни вибраций, напряжения и токи высоки, присутствует «идеальный шторм» факторов, которые делают выбор подходящего конденсатора особенно важной задачей.

Ключевые слова
Проблема микрофонного эффекта и механических резонансов конденсаторов активно обсуждалась на протяжении многих лет, однако исследований по этому вопросу было достаточно мало. Во всяком случае, мало опубликованных исследований. Но те, что существуют, подтверждают мнение, что данный эффект может оказывать заметное влияние качества звучания.
К тому же, в некоторых случаях конденсаторы могут приводить к необычайно высоким уровням гармонических и интермодуляционных искажений. Понимание того, как и почему это происходит, позволяет разработчикам сосредоточить свои усилия на доработке электронной схемы и тщательном выборе электронных компонентов — таким образом, чтобы это принесло наибольшую пользу.
Глава 20. Конденсаторы
Для накопления разноименных электрических зарядов служит устройство, которое называется конденсатором. Конденсатор — система двух изолированных друг от друга проводников (которые часто называют обкладками конденсатора), один из которых заряжен положительным, второй — таким же по величине, но отрицательным зарядом. Если эти проводники представляют собой плоские параллельные пластинки, расположенные на небольшом рас-стоянии друг от друга, то конденсатор называется плоским.
Для характеристики способности конденсатора накапливать заряд вводится понятие электроемкости (часто говорят просто емкости). Емкостью конденсатора к той разности потенциалов и ):
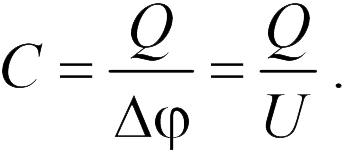
Поскольку величины (или и и . Поэтому в отношении (20.1) заряд сокращается.
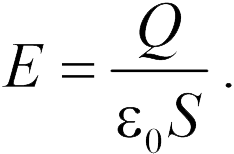
Выведем формулу для емкости плоского конденсатора (эта формула входит в программу школьного курса физики). При заряжении параллельных пластин, расположенных на небольшом расстоянии друг от друга, зарядами , в пространстве между ними возникает однородное электрическое поле с напряженностью (см. гл. 18):
Разность потенциалов между пластинами равна
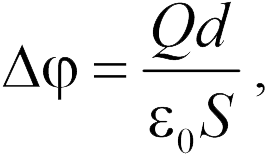
где — расстояние между ними. Отсюда, вычисляя отношение заряда к разности потенциалов (20.3), находим емкость плоского конденсатора
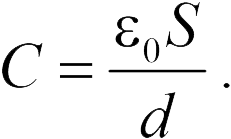
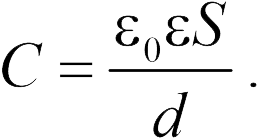
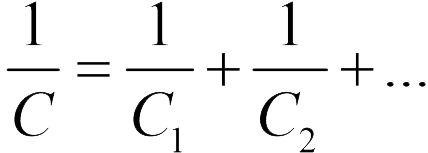
Для конденсаторов, соединенных в батареи, вводится понятие эквивалентной емкости, как емкости одного конденсатора, который при заряжении его тем же зарядом, что и батарея дает ту же разность потенциалов, что и батарея конденсаторов. Приведем формулы для эквивалентной емкости, а также для заряда и электрического напряжения на каждом конденсаторе при последовательном и параллельном их соединении.


Параллельное соединение (см. рисунок). В этом случае если сообщить левому проводнику заряд , заряд распределится между конденсаторами, вообще говоря, не одинаково, но по закону сохранения заряда .

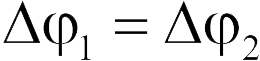
Поскольку правые пластины всех конденсаторов соединены между собой, левые — тоже, то они представляют собой единые проводники, и, следовательно, разность потенциалов между пластинами каждого конденсатора будет одинакова: . Можно доказать, что при таком соединении конденсаторов эквивалентная емкость батареи равна сумме емкостей отдельных конденсаторов
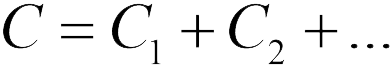
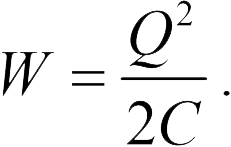
С помощью определения электрической емкости (20.1) можно переписать формулу (20.8) еще в двух формах:
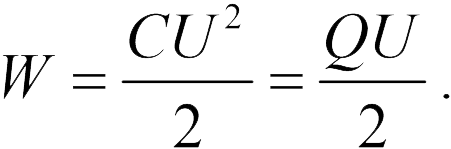
Рассмотрим в рамках этого минимума сведений о конденсаторах типичные задачи ЕГЭ по физике, которые были предложены в первой части книги.
Электроемкость конденсатора — его геометрическая характеристика, которая при неизменной геометрии не зависит от заряда конденсатора (задача 20.1.1 — ответ 3). Аналогично не меняется емкость конденсатора при увеличении напряжения на конденсаторе (задача 20.1.2 — ответ 3).
Связь между единицами измерений (задача 20.1.3) следует из определения емкости (20.1). Единица электрической емкости в международной системе единиц измерений СИ называется Фарада. 1 Фарада — это емкость такого конденсатора, между пластинами которого возникает напряжение 1 В при зарядах пластин 1 Кл и -1 Кл (ответ 4).

Поскольку электрическое поле в плоском конденсаторе однородно, то напряженность поля в конденсаторе связаны соотношением (см. формулу (18.9)) , где задаче 20.1.4

Согласно определению электрической емкости имеем в задаче 20.1.5

Из формулы (20.4) для емкости плоского конденсатора заключаем, что при увеличении площади его пластин в 3 раза (задача 20.1.6) его емкость увеличивается в 3 раза (ответ 1).
При уменьшении в раз. Поэтому новое напряжение на конденсаторе задача 20.1.7) можно найти из следующей цепочки формул

где — новый заряд конденсатора (ответ 3).
Так как конденсатор в задаче 20.1.8 подключен к источнику, то между его пластинами поддерживается постоянное напряжение изменяется при раздвигании пластин так же, как изменяется его емкость. А поскольку при увеличении расстояния между пластинами вдвое емкость конденсатора уменьшается вдвое (см. формулу (20.4)), то вдвое уменьшается и заряд конденсатора (ответ 2).
В задаче 20.1.9 конденсатор отключен от источника в процессе сближения пластин. Поэтому не меняется их заряд. А поскольку напряженность электрического поля между пластинами определяется соотношением (20.2)


то напряженность электрического поля между пластинами также не изменяется (ответ 3). Этот же результат можно получить и через определение емкости с учетом того, что
произведениеПри последовательном соединении конденсаторов (задача 20.2.1) одинаковыми будут их заряды независимо от значений их электрических емкостей (ответ 2). При параллельном соединении конденсаторов (задача 20.2.2) одинаковыми будут напряжения на каждом из них (ответ 3).
Поскольку конденсатор в задаче 20.2.3 отключен от источ-ника напряжения, его заряд не меняется в процессе раздвигания пластин. Поэтому для исследования изменения энергии конденсатора удобно воспользоваться формулой (20.8)
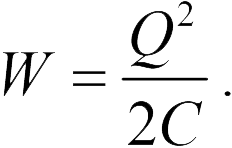
Так как при увеличении расстояния между пластинами в раз, то согласно формуле (1) энергия конденсатора увеличится в 1).
В задаче 20.2.4 не изменяется напряжение на конденсаторе. Поэтому воспользуемся первой из формул (20.9)
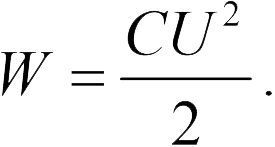
Из этой формулы заключаем, что при увеличении в раз — ответ 2. (Разница с предыдущей задачей связана с тем, что здесь кроме внешних сил, совершающих работу при раздвигании пластин, совершает работу источник напряжения.)
В задаче 20.2.5 изменяют расстояние между пластинами (и, следовательно, емкость) и заряд конденсатора. Поэтому удобно воспользоваться формулой (20.8)

Из этой формулы заключаем, что при увеличении расстояния между пластинами в 2 раза и увеличении заряда конденсатора в 2 раза его энергия возрастет в 8 раз (ответ 4).

Поскольку в задаче 20.2.6 конденсаторы соединены последовательно, емкость батареи конденсаторов можно найти по формуле (20.6), откуда находим емкость батареи конденсаторов (ответ 2).

В задаче 20.2.7 конденсаторы соединены параллельно, поэтому емкость батареи конденсаторов можно найти по формуле (20.7): (ответ 2).


Основной вопрос, на который нужно ответить в задаче 20.2.8, это как соединены конденсаторы? Последовательно, параллельно, по-другому? Попробуем по-другому расположить в пространстве и изменить длину соединительных проводов, чтобы схема стала более понятной. Очевидно, что можно соединить вершину 1 и вершину 3 («уменьшив» длину провода 1-3), а также вершины 2 и 4. При этом средний конденсатор разворачивается в пространстве, и схема приобретает вид, показанный на рисунке, откуда видно, что конденсаторы соединены параллельно. Поэтому (ответ 1).

Когда в заряженный плоский конденсатор вставляют металлическую пластинку (задача 20.2.9), параллельную обкладкам конденсатора, напряженность электрического поля внутри пластинки становится равным нулю, вне пластинки между обкладками конденсатора остается таким же, каким оно было в отсутствие пластинки , где — площадь его пластин. Поэтому напряжение между обкладками конденсатора

где — толщина пластинки. Отсюда находим емкость рассматриваемого конденсатора

Чтобы найти емкость сферического конденсатора (задача 20.2.10) сообщим его обкладкам заряды , найдем напряжение между обкладками, вычислим отношение заряда к напряжению. Разность потенциалов двух концентрических сфер, заряженных зарядами (напряжение между обкладками сферического конденсатора), определена в задаче 19.2.5., откуда находим электрическую емкость сферического конденсатора (ответ 3):
Читайте также:
