Металлическая балка переменного сечения
В производстве зданий из металлоконструкций имеют тенденцию к уменьшению их металлоемкости. В этом контексте сварные балки переменного сечения решают проблему уменьшения массы несущих конструкций.
В балке переменного сечения , работающей на изгиб, наиболее напряженная зона – полка. Стенка нагружена в меньшей степени. Следовательно, основная масса металла должна находиться в полках, а в стенках – меньше.
Сварка позволяет создавать рациональные и разнообразные профили с большим количеством. Именно благодаря применению сварки удается создавать балки разнообразных размеров – высотой до 3-4 м и более. Сварка позволяет наиболее рациональным образом сочетать размеры горизонтальных листов, называемых поясами, с вертикальной стенкой. Поэтому применяются балки с относительно толстыми полками в сочетании с высокими тонкими стенками.
Сварные же балки имеют больше вариантов исполнения, и дают возможность выпуска конструкций с любым необходимым соотношением размеров и технических данных. Балки собирают на сборочных станах путем сварки полосовой стали, раскроенной под проектные размеры полок и стенки двутавра.
Таким образом, можно сварить балку любого поперечного сечения, заданного проектом, в том числе и балку переменного сечения.
Особое распространение балка переменного сечения получила в авиационных ангарах , сельско-хозяйственных зданиях, складских-логистических комплексах , торговых зданиях там где значение имеет не только металлоемкость но и эстетические свойства и отсутствие излишней геометрической нагруженности конструктива здания,в сравнение с конструкциями из ферм болшое пространоство под потолком остается свободным от ненужных элементов при сохранение емкости и надежности металлоконструкции.


Балка переменного сечения в металлокаркасе
Страной где первыми стали применять подобную технологию были страны северной Америки : Сша и Канада, инженеры этих стран первыми научились рассчитывать и произвели оборудование для изготовления переменной балки, и уже оттуда они распространились по всему миру. На сегодняшний день практически все крупные международные компании по производству металлических ангаров активно применяют эту технологию и даже усовершенствовали его начав производить перфорированную балку и гофробалку. Зарождение производства переменных балок было обусловлено необходимостью возводить легкие и прочные каркасы авиационных военных ангаров в кратчайшие сроки с возможностью дальнейшего перенесения обьекта на другую территорию. Сейчас на передний план вышли другие преимущества это сниженный вес ,в сравнение с прокатным двутавровым профилем , дешевизна сырья , ведь чаще лист стоит дешевле чем профильные трубы и двутавр, ну и удобство транспортировки тут переменная балка на голову опережает крупногабаритные фермы.
Большим преимуществом балки является величина ее приведенного сечения ,те кто знакомы с расчетами конструкций на противопожарную безопасноть знают что величина не менее 15 экономить на огнезащите конструкций и делает здание более огнестойким по сравнению с тонкостенными конструкциями. Приведенное сечение положительно влияет и на долговечность кострукции , массивная конструкция имеет преимущество при расчете усталостной прочности металла под воздействием динамических нагрузок , долще поверхность не разрущается мелкими трещинами ,а значит дольше прослужит в плане антикоррозионной стойкости и сохранение прочности.
Расчет и проектирование балок переменного сечения производится по СНиП II-23-81 но к сожалению на сегодняшний день нет более точной утвержденной методики подходящей именно переменной балки , в связи с этим ранее были некоторые проблемы с прохождением экспертиз , но на сегодняшний день наши конструктора нашли решения этого вопроса и мы с уверенностью получили положительное заключение в 5 регионах России. Болтовые соединения основа узлов в подобных конструкциях , узлы на сварке встречаются крайне редко так как портят и эстетику здания и могут нанести вред лкп металлоконструкции , болтовое соединения является современным решением очень удобным в монтаже. Оцинкованные гнутые прогоны это еще одна часто встречающаяся составляющая конструкций из переменной балки , легкие и прочные они прекрасно работают в этой технологии уменьшая нагрузку на балку и придавая конструкции еще более современный и индустриальный вид.
Расчет балок переменного сечения
В данной статье рассматриваются принципы расчета балок не равного сопротивления изгибающему моменту, т.е. таких балок прямоугольного сечения, один из геометрических параметров поперечного сечения которых уменьшается обратно пропорционально действующему изгибающему моменту. Основные принципы расчета таких балок такие же, как и балок равного сопротивления изгибающему моменту, но есть некоторые особенности.
1. Расчет балок прямоугольного сечения, изменение одного из геометрических параметров сечения которой носит обратный характер, может выполняться на основании следующих предположений:
1.1. Так как ни один из геометрических параметров, например, ширина шарнирно опертой балки изменяться от b в начале пролета, до 0 в середине пролета не может (такая балка разрушится), то сначала выполняется расчет по прочности и исходя из этого расчета определяются геометрические параметры наиболее нагруженного сечения. Следовательно такую балку можно рассматривать как две балки: одну с постоянной шириной, а вторую с шириной изменяющейся от Δb до 0. При этом эпюра моментов характеризует прогиб для балки постоянного сечения, а кроме того эту эпюру можно рассматривать, как эпюру нормальных напряжений для балки постоянного сечения.
1.2. Общая эпюра нормальных напряжений, возникающих в поперечных сечениях балки, характеризует общий прогиб балки.
1.3 Если наложить эпюру моментов на эпюру напряжений балки переменного сечения, то соблюдении определенных условий разница между этими эпюрами покажет изменение прогиба для балки переменного сечения.
Точнее разность площадей этих эпюр можно рассматривать как некую фиктивную нагрузку и тогда разница этих эпюр покажет изменение фиктивной опорной реакции А, а при делении полученного значения на жесткость - изменение угла поворота на опоре А. Тогда фиктивный момент (фиктивная опорная реакция, умноженная на расстояние от точки приложения фиктивной опорной реакции до рассматриваемой точки, минус площадь разностной эпюры, умноженная на расстояние от центра тяжести разностной эпюры до рассматриваемой точки) покажет изменение прогиба.
Примечание: принципы графоаналитического метода в данной статье на рассматриваются.
Например, для балки с линейно изменяющейся шириной b разностная эпюра будет выглядеть так:
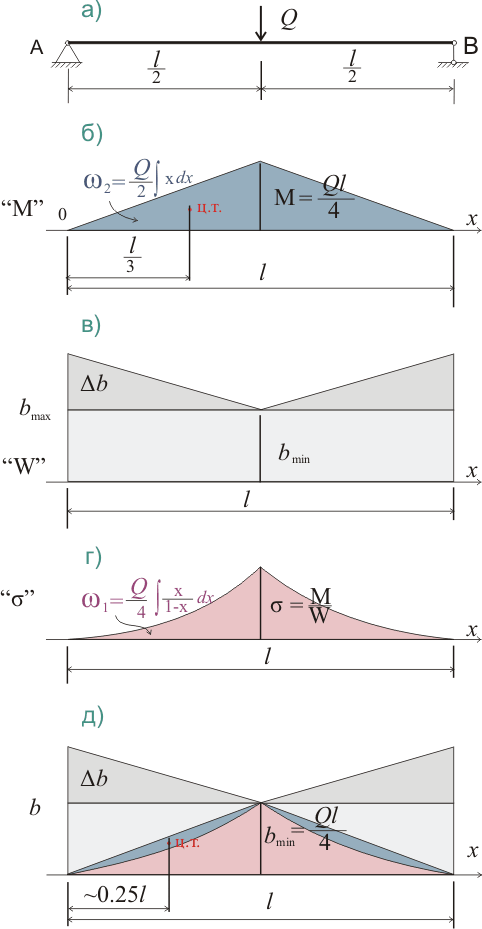
Рисунок 323.1.1
При этом на разностную эпюру будет влиять не только характер нагрузки на балку, но также и величина отклонения от минимально допустимого размера поперечного сечения. Так, если Δb → 0, то сечение балки стремится к постоянному значению. При значительном увеличении Δb по сравнению с b уменьшается эффективность использования материала, хотя при этом и прогиб уменьшается. Условие Δb → b не допускается принятыми в п.1.1 ограничениями. Поэтому расчет балок с сечением, уменьшающимся от начала балки к середине, зависит от значения bmin. Кроме того, от значений bmin и Δb зависит характер изменения нормальных напряжений.
Прогиб балки с линейно уменьшающейся шириной сечения при сосредоточенной нагрузке посредине пролета
1.4. Так как изменение нормальных напряжений для балки с сосредоточенной нагрузкой описывается зависимостью вида:
σ = М/W = 6Ax/bh 2 (323.1.1)
то при постоянном значении h 2 /6 = C = 1 формула (323.1.1) примет вид:
σ = Qx/2C(b - bminy) = Qx/2(nbmin - bminy) (323.1.2)
После соответствующих преобразований получим следующую зависимость:
bminσ = Qx/2(n - y) (323.1.3)
Где bmin в данном случае постоянная величина и ее значение также можно принять равным 1. Тогда например, при Δb = bmin = b/2, n = 2, у = 2х, разностная эпюра описывается двумя линиями, имеющими следующую зависимость:
В данном случае значение опорной реакции А = Q/2 - постоянная величина и для упрощения расчетов ее можно вынести за пределы интегрирования. Данные линии пересекаются в точках 0 и 0.5 (начало балки и середина пролета или нижний и верхний предел интегрирования), тогда:
ω2 = (Q/2)∫хdx = (Q/2)(x 2 /2) = (Q/2)(l 2 /8) = Ql 2 /16 (323.2.2)
ω1 = (Q/2)(1/2)∫(x/(1-x))dх = (Q/4)(-x - ln(1 - x)) = (Q/4)(0.193147)l 2 = 0.772588Ql 2 /16 (323.2.3)
тогда площадь разностной эпюры составит:
ωр = ω2 - ω1 = Ql 2 /16 - 0.77288Ql 2 /16 = 0.22712Ql 2 /16 (323.2.4)
Примечание: В данном случае нас интересует разностная эпюра потому, что определить расстояние до центра тяжести разностной эпюры намного проще, чем искать центр тяжести для эпюры с площадью ω1. Визуально (рис.323.1 д) это расстояние составляет l/4. Кроме того для визуальной оценки результатов интегрирования для эпюр моментов и напряжений на рисунках 323.1 - 323.3 сначала строились графики функций (см. рис.323.1.2).
Значение фиктивного изгибающего момента составит:
Mф = Ql 2 /16(l/3) - (0.22712Ql 2 /16)(l/4) = Ql 3 /48 - 0.17Ql 3 /48 = 0.83Ql 3 /48 (323.2.5)
fпр = 0.83Ql 3 /48EIbmin (323.2.6)
В данной случае Ibmin означает, что мы рассматриваем изменение прогиба по отношению к балке с постоянным моментом инерции и соответственно постоянной шириной сечения bmin.
Чтобы было еще более наглядно, для рассматриваемого случая увеличение материала балки в 1.5 раза приводит к уменьшению прогиба в 1.184 раза.
Если изменение ширины сечения будет описываться другой зависимостью, то приближенные результаты можно получить интерполяцией данных рисунка 323.1.2.
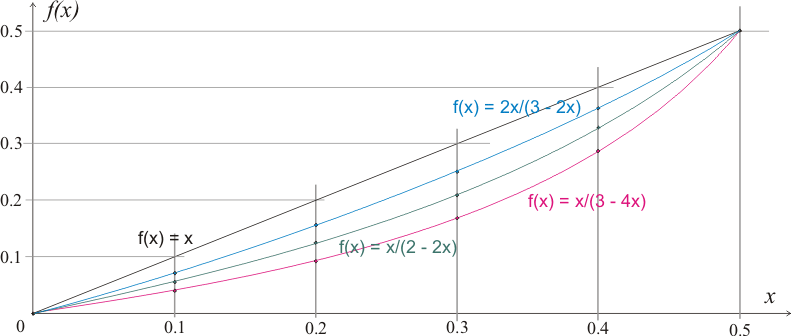
Рисунок 323.1.2
Как видно из данного рисунка, при соотношении Δb/b = 1/3 (f(x) = 2x/(3 - 2x)) площадь разностной эпюры будет приблизительно в 2 раза меньше, чем при рассматривавшемся соотношении 1/2. При соотношении 2/3 площадь разностной эпюры увеличится приблизительно на 1/2.
Прогиб балки с линейно уменьшающейся шириной сечения при равномерно распределенной нагрузке
При равномерно распределенной нагрузке изменится и эпюра моментов и эпюра нормальных напряжений
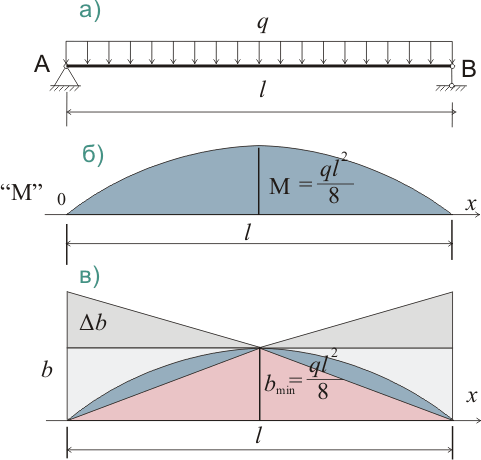
Рисунок 323.2
σ = М/W = 6(qlx - qx 2 )/2bh 2 (323.4.1)
то при постоянном значении h 2 /3 = C =1 формула 323.1.1) примет вид:
σ = (qlx - qx 2 )/C(nbmin - bminy) (323.4.2)
bminσ = (qlx -x 2 )/(n - y) (323.4.3)
При bmin ;= 1, при Δb = bmin = b/2, n = 2, у = 2х, разностная эпюра описывается двумя линиями, имеющими следующую зависимость:
f1(x) = (qlx - qx 2 ); f2(x) = (qlx - qx 2 )/2(1- x) (323.4.4.1)
Данные линии пересекаются в точках 0 и 0.5 (начало балки и середина пролета или нижний и верхний предел интегрирования), тогда:
ω2 = q∫(lх - x 2 )dx = q(l∫xdx - ∫x 2 dx) = q(l 3 /8 - l 3 /24) = ql 3 /24 (323.4.5.1)
ω1 = (q/2)(l∫x/(1-x) - ∫(x 2 /(1-x))dх = (ql/2)(0.193147)l 2 - (q/2)(0.068147)l 3 = ql 3 /32 (323.4.6.1)
ωр = ω2 - ω1 = ql 3 /24 - ql 3 /32 = ql 3 /96 = 0.25ql 3 /24 (323.4.7)
Тогда значение фиктивного изгибающего момента составит:
Mф = ql 3 /24(5l/16) - (ql 3 /96)(l/4) = 5ql 4 /384 - ql 4 /384 = ql 4 /96 = 4ql 4 /384 (323.4.8)
fпр = 4ql 4 /384EIbmin (323.4.9)
В данной случае Ibmin также означает, что мы рассматриваем изменение прогиба по отношению к балке с постоянным моментом инерции и соответственно постоянной шириной сечения bmin.
Чтобы было еще более наглядно, при равномерно распределенной нагрузке увеличение материала балки в 1.5 раза приводит к уменьшению прогиба в 1.2 раза.
Если длину балки также принять за некую единицу, что допустимо при выбранных нами пределах интегрирования, то уравнения функций будут выглядеть так:
f1(x) = (q/2)x(1 - x); f2(x) = (q/4)x(1 - x)/(1- x) = qx/4 (323.4.4.2)
Т.е. в данном случае график, описывающий эпюру напряжений, имеет линейную зависимость (рис.323.2 в).
ω2 = (q/2)∫x(1 - x)dx = (q/2)(1/12) = q/24 = ql 3 /24 (323.4.5.2)
ω1 = (q/4)∫xdх = (q/4)(x 2 /2) = (q/4)(1/8) = ql 3 /32 (323.4.6.2)
Прогиб балки с линейно уменьшающейся высотой при сосредоточенной нагрузке посредине балки
Так как момент сопротивления W = bh 2 /6 для прямоугольного сечения, то даже при линейно уменьшающейся высоте зависимость между нормальными напряжениями и эпюрой моментов будет не линейной даже при сосредоточенной нагрузке, приложенной посредине балки. При равномерно распределенной нагрузке определение прогиба методом интегрирования еще более усложнится. Но в целом влияние изменения высоты на прогиб изменится, так как в данном случае следует рассматривать не изменяющуюся высоту, а квадрат изменяющейся высоты, а так как момент инерции это I = bh 3 /12 для прямоугольного сечения, то эпюру моментов следует сравнивать с кубическим изменением высоты сечения.
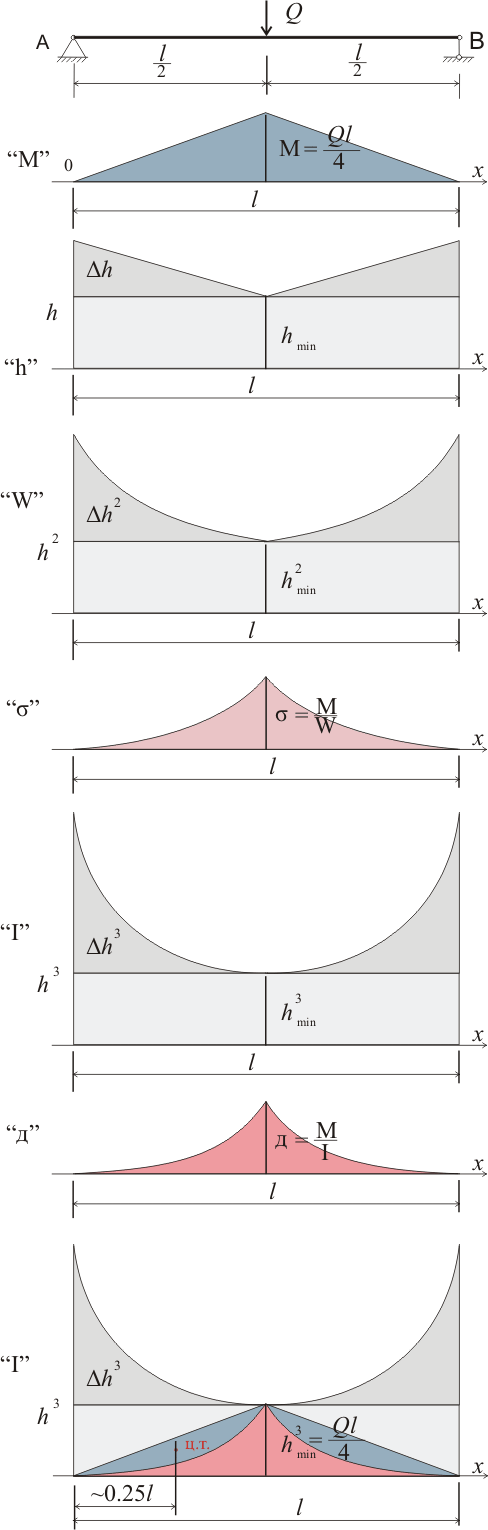
Рисунок 323.3
При Δh = hmin = h/2, n = 2, у = 2х, разностная эпюра описывается двумя линиями, имеющими следующую зависимость:
f1(x) = Qx/2; f2(x) = Qx/16(1- x) 3 (323.5.1)
ω2 = (Q/2)∫хdx = (Q/2)(x 2 /2) = (Q/2)(l 2 /8) = Ql 2 /16 (323.5.2)
ω1 = (Q/2)(1/8)∫(x/(1-x) 3 )dх = (Q/16)(1/2) = Ql 2 /32 (323.5.3)
ωр = ω2 - ω1 = Ql 2 /16 - Ql 2 /32 = Ql 2 /32 (323.5.4)
Mф = Ql 2 /16(l/3) - Ql 2 /32(l/4) = Ql 3 /48 - Ql 3 /128 = (1 - 0.375)Ql 3 /48 = 0.625Ql 3 /48 (323.5.5)
fпр = 0.625Ql 3 /48EIbmin (323.5.6)
Примечание: расстояние от центра тяжести разностной эпюры до начала координат определено визуально по рисунку 323.3.
Прогиб балки с линейно уменьшающейся высотой сечения при равномерно распределенной нагрузке
Так как при линейно уменьшающейся ширине сечения разница в прогибах при сосредоточенной нагрузке, приложенной посредине пролета и равномерно распределенной нагрузке крайне незначительна, то можно предположить, что такая же незначительная разница будет и при линейно изменяющейся высоте сечения. Тогда при Δh = hmin = h/2
fпр ≈ 3ql 4 /384EIbmin (323.6.6)
Прогиб балки с высотой сечения, уменьшающейся пропорционально изгибающему моменту
Примером такой балки является любая шарнирно опертая железобетонная балка с трещинами в растянутой зоне. В результате действия нормальных напряжений высота сжатой зоны сечения балки изменяется нелинейно. Эту зависимость можно приблизительно выразить так:
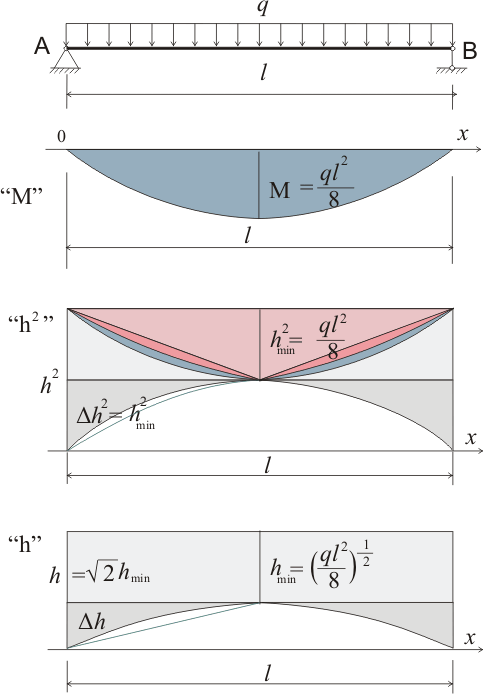
Рисунок 323.4
Железобетонная балка с арматурой в растянутой зоне может рассматриваться как балка переменного сечения. В поперечных сечениях, в которых изгибающий момент равен нулю или очень мал, сжимающие напряжения вызывают упругие деформации бетона, растягивающие напряжения вызывают упругие деформации и бетона и арматуры. При выбранной расчетной схеме сжимаемой будет верхняя часть сечения, а растягиваемой нижняя часть сечения. После того, как растягивающие напряжения достигнут предела прочности бетона при растяжении, бетон в растягиваемой зоне начнет разрушаться - начнут образовываться трещины - и потому с увеличением растягивающих напряжений все большую часть этих напряжений будет воспринимать арматура и все меньшую часть бетон нижней части сечения. Таким образом будет уменьшаться высота приведенного сечения балки. Минимальной высота приведенного сечения будет в точке действия максимального изгибающего момента.
При этом увеличение изгибающего момента будет приводить к уменьшению квадрата высоты сжатой зоны сечения (эпюра "h 2 "). На эпюре "h 2 " также показано влияние нелинейного изменения высоты сечения по сравнению с линейным изменением высоты сечения. При подобном нелинейном изменении высоты площадь разностной эпюры при соотношении hmin = h/2 будет в 2 раза меньше, чем при линейном изменении высоты.
Если рассматривать только упругие деформации сжатой области поперечных сечений бетона, то уменьшение квадрата высоты в два раза означает изменение высоты Δh от 0 до hmin/√ 2 .
Таким образом, используя данные, полученные при рассмотрении балок с линейно уменьшающейся шириной и высотой сечения, суммарное влияние нелинейного изменения высоты и изменения соотношения hmin/h можно выразить так:
fпр ≈ 5ql 4 /384EIhmin - 2ql 4 /(384·2·1.41EIhmin) = (5 - 0.7)ql 4 /384EIhmin ≈ 4.3ql 4 /384EIhmin ≈ 0.86·5ql 4 /384EIhmin (323.7.6.1)
При этом 0.86 можно рассматривать как значение поправочного коэффициента, учитывающего изменяющуюся высоту балки.
Соответственно, если по каким-либо причинам изменение высоты сечения составит h/2, то
fпр ≈ 5ql 4 /384EIhmin - 2ql 4 /(384·2·EIhmin) = (5 - 1)ql 4 /384EIhmin ≈ 4ql 4 /384EIhmin ≈ 0.8·5ql 4 /384EIhmin (323.7.6.2)
Если изменение высот будет от 0 до hmin/2√ 2 , то
fпр ≈ 5ql 4 /384EIhmin - 2ql 4 /(384·2·2·1.41EIhmin) = (5 - 0.35)ql 4 /384EIhmin ≈ 4.65ql 4 /384EIhmin ≈ 0.93·5ql 4 /384EIhmin (323.7.6.3)
На этом пока все.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье "Записаться на прием к доктору"
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Для Украины - номер гривневой карты (Приватбанк) 5168 7422 4128 9630
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье "Записаться на прием к доктору" (ссылка в шапке сайта).
Балки переменного сечения
В строительстве нередко используются элементы конструкций, имеющие ярко выраженное переменное по длине сечение. Например любую железобетонную балку, в растягиваемой зоне которой возникают трещины, можно рассматривать как балку переменного сечения. В связи с этим расчет балок переменного сечения представляет определенный интерес.
Очень часто при расчете строительных конструкций рассматриваются элементы, имеющие постоянное по длине поперечное сечение. Именно такое сечение как правило рассматривается при определении прочности и прогибов изгибаемых элементов. Чаще всего в качестве изгибаемых элементов рассматриваются прямолинейные стержни - балки.
Между тем такое возможно только в теории, в природе физических тел постоянного сечения не существует. Металлопрокат, используемый для изготовления большого количества строительных конструкций, имеет некоторые отклонения от геометрических размеров, эти отклонения нормируются ГОСТами. Для деревянных брусьев, используемых как балки, стойки, подкосы и т.д. и изготавливаемых на различном оборудовании, относительная величина отклонений может быть еще больше. А у бетонных и железобетонных элементов геометрические размеры зависят от качества и точности выставления опалубки, а также от соблюдения технологических требований.
Кроме того в природе не существует абсолютно изотропных материалов, все конструкционные материалы рассматриваются как изотропные с некоторой степенью условности.
Тем не менее рассматривать элементы конструкции, как некие тела, имеющие постоянное сечение, при небольших относительных отклонениях от геометрической формы вполне допустимо, так как погрешность расчетов в таких случаях не превышает 0.1-1%. К тому же при расчетах на прочность используются не нормативные значения сопротивления материала, а расчетные - полученные в результате деления нормативного значения на коэффициент, учитывающий максимально возможные отклонения от нормативных значений, возникающие в результате неоднородности материала, погрешностей геометрии и т.п.
Однако в строительстве нередко используются элементы конструкций, имеющие ярко выраженное переменное по длине сечение. Например, любую железобетонную балку, в растягиваемой зоне которой возникают трещины, можно рассматривать как балку переменного сечения, так как приведенная высота сечения сжимаемого бетона в месте действия максимального изгибающего момента уменьшается в 1.5-2 раза в результате образования трещин в растягиваемой зоне.
Балки переменного сечения по характеру изменения размеров поперечного сечения можно разделить на 4 основных вида:
Геометрическими параметрами поперечного сечения являются высота и ширина сечения. Определение высоты и ширины зависит от выбора системы координат.
1. Балки ступенчатого сечения
К балкам ступенчатого сечения относятся балки, имеющие постоянное сечение на протяжении некоторого участка, скачкообразно изменяющееся в начале и конце участка. В зависимости от того, какой именно параметр изменяется, балки переменного сечения можно разделить на несколько подвидов:
1. а. Балки со ступенчато изменяющейся шириной поперечного сечения.
1.б. Балки со ступенчато изменяющейся высотой сечения. К таким балкам можно отнести монолитные железобетонные перекрытия по ригелям. Если рассматривать такие перекрытия, как однопролетные, то ригели будут локальными изменениями высоты сечения. Между тем более правильно такие перекрытия рассматривать, как многопролетные неразрезные балки, при этом ригеля являются дополнительными упругими опорами, но если крайние пролеты имеют усиленное армирование для восприятия моментов, максимальных в крайних пролетах, то даже при постоянной высоте сечения такие перекрытия можно рассматривать, как балки со ступенчато изменяющейся высотой сечения в крайних пролетах. Дело в том, что железобетон - композитный материал и приведенный центр тяжести сечения, через который проходит ось стержня изменяет свое положение не только при появлении трещин, но и при изменении диаметра арматуры.
1.в. Балки со ступенчато изменяющейся высотой и шириной сечения. Примером таким балок являются валы с выточками.
2. Балки постоянной высоты и переменной ширины
2.а. Изменение ширины можно выразить линейной зависимостью.
2.б. Изменение ширины можно выразить другой математической зависимостью.
2.в. Изменение ширины очень трудно выразить математической зависимостью.
3. Балки постоянной ширины и переменной высоты
3.а. Изменение высоты можно выразить линейной зависимостью.
3.б. Изменение высоты можно выразить другой математической зависимостью. К таким балкам можно отнести железобетонные элементы прямоугольного сечения с трещинами в растянутой зоне сечения.
3.в. Изменение высоты очень трудно выразить математической зависимостью.
4. Балки переменной высоты и ширины
4.а. Изменение высоты и ширины можно выразить линейной зависимостью.
4.б. Изменение высоты ширины можно выразить другой математической зависимостью. К таким балкам можно отнести железобетонные элементы непрямоугольного сечения с трещинами в растянутой зоне.
4.в. Изменение высоты ширины очень трудно выразить математической зависимостью.
Отдельный интерес представляют балки с перфорированной стенкой и фермы, которые также можно рассматривать как балки переменного сечения, если соединение в узлах не шарнирное, а жесткое. Ну а кто выполнял расчет для всех растений и животных, да и для самого человека - до сих пор остается загадкой, известно лишь то, что расчеты эти выполнены с непостижимой для человеческого ума точностью и предусмотрительностью, ну а безукоризненная реализация этих расчетов вызывает еще большее восхищение. Достаточно взглянуть на ближайшее дерево, представляющее собой с точки зрения строительной механики жестко защемленный непрямолинейный стержень очень переменного сечения. При этом дерево не только выдерживает снеговые, ветровые нагрузки, нагрузки от многочисленных птиц, животных, иногда человека, но еще и живет своей малопонятной жизнью.
Человек пока не научился создавать подобные конструкционные материалы, зато очень хорошо научился пользоваться природными материалами. Например, наши предки использовали изделия из древесины в качестве балок перекрытия, причем на заре строительства, когда из деревообрабатывающего оборудования у человека был только кремниевый топор, эти балки были переменного сечения, так как представляли собой бревна, имевшие различный диаметр в начале и конце балки. При этом никаких особенных расчетов, как это принято сейчас, не делалось. Так как ни строительная механика, ни теория сопротивления материалов, ни даже сам язык, используемый человеком для общения, еще не сформировались.
Сейчас, когда разделы физики, изучающие закономерности взаимодействия сил и особенности возникновения напряжений в различных материалах, достигли значительных успехов, а строительные технологии поднялись на очень высокий уровень, балки переменного сечения используются еще чаще, а в будущем интерес к балкам переменного сечения будет только возрастать, в основном потому, что человек стремится использовать окружающий его мир на все 100%, а современные балки постоянного сечения, материал которых используется на 20-40% станут непозволительной роскошью.
Впрочем, особенности расчета балок переменного сечения - это отдельная тема.
Металлическая балка переменного сечения
Однопролетные строительные конструкции могут опираться на что угодно и закреплены при этом могут быть по-разному. Металлические и железобетонные перемычки, плиты перекрытия как правило укладываются на цементно-песчаный раствор, деревянные балки перекрытия могут быть прибиты гвоздями или прикручены шурупами или просто оперты на стены, элементы железобетонного каркаса обычно соединяются с помощью электросварки и бетонирования, металлические конструкции могут быть соединены при помощи сварки, болтов или заклепок. Но строительная механика таких способов опирания и закрепления не знает, а предлагает нам для расчетов совсем другие варианты опор, из которых самые распространенные - это шарнирное опирание и жесткое защемление на опоре. А ведь при расчете строительных конструкций одна их первейших задач - это определение опорных связей, проще говоря, выбор опор. Понять, почему это так важно, поможет следующий пример:
Расчетые схемы наклонных балок
Расчет наклонных балок вообще и стропил в частности имеет одну интересную особенность. Одни авторы утверждают, что в наслонных стропилах нормальных напряжений растяжения или сжатия при действии вертикальной нагрузки не возникает. Другие - что эти напряжения хоть и возникают, но крайне незначительны и их значением для упрощения расчетов можно пренебречь. Третьи - что учитывать нормальные напряжения при расчете наклонных балок все-таки нужно.
Из-за чего же возникает такое разнообразие мнений и самое главное: как поступить простому человеку при расчете стропильной системы? Давайте попробуем разобраться.
Общий случай расчета балки на шарнирных опорах при действии нескольких сосредоточенных нагрузок
Первый этап расчета однопролетной балки на шарнирных опорах - определение максимальных изгибающих моментов, поперечных сил, углов поворота и прогибов - большой сложности не представляет, если к балке приложена одна сосредоточенная нагрузка. Все необходимые формулы для этого частного случая уже имеются, достаточно лишь подставить в эти формулы свои значения.
Тем не менее очень часто балка бывает загружена несколькими сосредоточенными нагрузками. Если эти нагрузки равны и приложены симметрично, то наиболее простой способ расчета такой балки - перевести сосредоточенные нагрузки в эквивалентную равномерно распределенную.
Однако в общем случае сосредоточенные нагрузки к однопролетной балке на шарнирных опорах могут быть приложены не симметрично, да и значения сосредоточенных нагрузок могут быть разными. И в этом общем случае для получения точных результатов отделаться малой кровью не получится, необходимо выполнять полный расчет по общему протоколу.
Расчет балки. Общие положения
Расчет любой балки состоит из двух основных этапов. Первый этап - определение максимальных напряжений, действующих в поперечных сечениях балки. Второй этап - выбор материала балки и определение характеристик сечения, удовлетворяющих условиям, определенным на первом этапе.
Таким образом на первом этапе расчетов знать материал, из которого будет изготавливаться балка, расчетное сопротивление и прочие характеристики материала вовсе не обязательно. В связи с этим расчет балки на первом этапе - задача строительной механики, а второй этап - удел теории сопротивления материалов.
А теперь рассмотрим каждый из этих этапов более подробно.
К расчету балок на упругом основании
В малоэтажном строительстве, как впрочем и в любом другом, балки на упругом основании встречаются намного чаще, чем это можно подумать. По той причине, что любой ленточный фундамент, а иногда и плитный фундамент можно рассматривать как балку на упругом основании.
И если с расчетом балки - ленточного фундамента проблем практически не возникает по той простой причине, что нагрузка на ленточный фундамент как правило равномерно распределенная, а значит и фундамент ведет себя, как абсолютно жесткая балка, дополнительных расчетов не требующая. То при рассмотрении участка плитного фундамента как балки или ленточного фундамента с неравномерно приложенной нагрузкой могут возникнуть некоторые проблемы.
Расчет балки из разнородных материалов
Балки из разнородных материалов встречаются в малоэтажном строительстве достаточно редко. Тем не менее, все-таки встречаются и потому следует понимать, как подобные балки рассчитываются.
Например, если к деревянной балке перекрытия прикрепить снизу (или сверху) металлическую полосу, то это и будет балка из разнородных материалов. Расчет железобетонных балок, которые также могут рассматриваться как балки из разнородных материалов, в данной статье не рассматривается, так как это отдельная большая тема.
Примечание: Как именно будет осуществляться крепление, чтобы обеспечить совместную работу материалов, в данной статье не рассматривается. Основное внимание будет уделено принципам расчета подобной балки. И металлическую полосу лучше крепить снизу, чтобы металл работал на растяжение, а не на сжатие.
Виды балок
С тех пор как наши предки вышли из пещер и занялись возведением жилья из подручных материалов, одной из самых важных проблем строительства остается вопрос изготовления перекрытия, проще говоря, крова над головой. Для перекрытия небольших пролетов (1-6 м) издревле использовались деревянные балки - бревна. Для перекрытия бóльших пролетов изготавливались достаточно сложные арочные плоские или пространственные конструкции из камня, кирпича и даже бетона, имитирующие небесный свод.
Нужно отдать должное нашим предшественникам, не имея ни малейших представлений о теории сопротивления материалов, строительной механике и прочих мудреных дисциплинах, не пользуясь электроинструментом, автомобилями, одним словом обладая минимальной технической базой, они уже строили храмы и святилища и мосты с пролетами в несколько десятков метров, причем некоторые из них сохранились до наших дней.
Расчет балок равного сопротивления изгибающему моменту
Расчет на прочность балок равного сопротивления изгибающему моменту, другими словами балок, нормальные напряжения в поперечных сечениях которых постоянны, мало чем отличается от расчета балок постоянного сечения, так как требования по прочности остаются неизменными - напряжения в максимально нагруженном сечении не должны превышать максимально допустимых. А вот определение деформаций балок равного сопротивления изгибающему моменту имеет свои особенности.
Вопрос по креплению консоли с подпором
19-07-2015: Bespalovs
Встал следующий вопрос. Консоль имеет вылет 1600 мм. Распределенная нагрузка 2.7 кгс см.
В приведенном виде, по моему мнению, это конструкция, состоящая из стержней, соединенных шарнирами.
Необходимо определить наиболее экономичный способ реализации.(тип металлической балки – сечение, тип подкоса и вариант его установки (снизу или сверху)
Консольная балка с загруженными консолями
На первый взгляд такой вариант загружения балки - симметрично загруженные консоли и отсутствие нагрузки посредине - может показаться достаточно редким и потому необходимость расчета такой консольной балки - сомнительной. Но не будем торопиться с выводами и определим, в чем особенность работы балки с симметрично загруженными консолями.
Для простоты рассмотрим балку, имеющую равные по длине консоли k, к которым приложена одинаковая по значению симметричная нагрузка. Например, имеется балка пролетом l, с равными консолями k, на концах которых приложена сосредоточенная нагрузка Q (рис. 384.1. а)):
К расчету консольных балок
Консольная балка - достаточно сложная балка, не смотря на кажущуюся простоту. Например, есть доска длиной 3 м, доска лежит на некоем основании шириной 1 м, при этом свесы доски с каждой из сторон составляют 1 м. На доску действует равномерно распределенная нагрузка 100 кг/м. И тут возникает вопрос: как рассчитать такую балку?
1 вариант
Вроде бы у балки одна опора и повороту поперечных сечений она не мешает и получается, что эту опору можно рассматривать как шарнирную. Вот только такого понятия, как ширина опоры, во всяком случае на первом этапе расчета, при рассмотрении расчетных схем балок не существует.
Получается, что нашу доску мы можем рассматривать как балку с одной опорой и 2 консолями. Если ширину опоры не учитывать, длина консолей будет k = 1 м, а максимальный момент, действующий на опоре, будет составлять:
Метод нулевых моментных точек
Использование метода нулевых моментных точек позволяет значительно упростить решение ряда задач строительной механики, связанных с расчетом статически неопределимых конструкций.
Суть метода нулевых моментных точек рассмотрим на примере однопролетной балки с жестким защемлением на одной их опор.
Расчет балки на действие распределенной и сосредоточенной нагрузок
Когда на балку действует несколько нагрузок: равномерно распределенная по всей длине и сосредоточенная посередине длины балки, то для упрощения расчетов сосредоточенную нагрузку можно перевести в эквивалентную равномерно распределенную.
Но в некоторых случаях, например при расчете плиты перекрытия на которую будут монтироваться перегородки, сосредоточенная нагрузка может быть приложена не посередине длины плиты и для определения максимального изгибающего момента требуется выполнить полный расчет. Этим мы сейчас и займемся.
Формулы для расчета балки с консолями на действие равномерно распределенной нагрузки
Если однопролетная балка с шарнирными опорами имеет консоли, разные по длине, то рассчитать такую балку по простым общеизвестным формулам из справочника не получится. Даже если на такую балку действует равномерно распределенная нагрузка.
Все из-за того, что формулы для определения опорных реакций, моментов, прогибов получаются достаточно громоздкими. Тем не менее ничего сложного в таких расчетах нет.
Шарнирно-опертая балка с трапециевидной распределенной нагрузкой
05.02.2016 Анна
Добрый день, Доктор
Со сложением опорных реакций, моментов и эпюры Q проблем конечно не возникло.
Меня очень интересует формула для определения прогибов и угла поворота для трапециевидной нагрузки вида 2.1+2.5, когда слева, скажем нагрузка q1, а справа q2. Или нагрузка для схемы 2.1 - q1, а для схемы 2.5 q2.
Никак не совладаю с формулой для определения максимального прогиба и прогиба вообще и угла поворота.
Подбор сечений балок равного сопротивления.
Все предыдущие расчеты относились к балкам постоянного сечения. На практике мы имеем часто дело с балками, поперечные размеры которых меняются по длине либо постепенно, либо резко.
Ниже рассмотрено несколько примеров подбора сечения и определения деформаций балок переменного профиля.
Так как изгибающие моменты обычно меняются по длине балки то, подбирая ее сечение по наибольшему изгибающему моменту, мы получаем излишний запас материала во всех сечениях балки, кроме того, которому соответствует . Для экономии материала, а также для увеличения в нужных случаях гибкости балок применяют балки равного сопротивления. Под этим названием подразумевают балки, у которых во всех сечениях наибольшее нормальное напряжение одинаково и должно быть равно допускаемому.
Условие, определяющее форму такой балки, имеет вид
Здесь М(х) и W(x) изгибающий момент и момент сопротивления в любом сечении балки; W(х) для каждого сечения балки должен меняться пропорционально изгибающему моменту.
Эти условия справедливы и для сечения с наибольшим изгибающим моментом; если обозначить момент сопротивления балки в сечении с наибольшим изгибающим моментом , то можно написать:
Покажем ход вычислений на примере. Рассмотрим балку пролетом l, защемленную концом А и нагруженную на другом конце силой Р (Рис.1). Выберем сечение этой балки в виде прямоугольника; задачу о надлежащем изменении момента сопротивления можно решать, меняя высоту или ширину балки или тот и другой размер вместе.
Рис.1. Расчетная схема балки равного сопротивления
Пусть высота балки будет постоянной , а ширина переменной. Момент сопротивления в сечении на расстоянии х от свободного конца будет , а изгибающий момент ; момент сопротивления опорного сечения , a наибольший изгибающий момент в опорном сечении . В расчете имеют значения лишь абсолютные величины М(х) и
По формуле (1) получаем:
т. е. ширина меняется по линейному закону в зависимости от х. При ширина равна .
Вид балки в фасаде и плане показан на Рис.1. Такое очертание балки получается, если учитывать ее прочность только по отношению к нормальным напряжениям; ширина в сечении В обращается в нуль.
Однако необходимо обеспечить прочность и по отношению к касательным напряжениям. Наименьшая ширина балки, требуемая этим условием, определится из уравнения
Таким образом, исправленное очертание балки предопределяет минимальный размер ширины и утолщение свободного края консоли.
Определение деформаций балок переменного сечения.
При определении прогибов и углов поворота для балок с переменным сечением надлежит иметь в виду, что жесткость такой балки является функцией от х. Поэтому дифференциальное уравнение изогнутой оси принимает вид
где J(x) переменный момент инерции сечений балки.
До интегрирования этого уравнения можно выразить J(x) надлежащей подстановкой через J, т. е. через момент инерции того; сечения, где действует ; после этого вычисления производятся так же, как и.для балок постоянного сечения.
Покажем это на примере, разобранном выше. Определим прогиб балки равного сопротивления, защемленной одним концом, нагруженной на другом конце силой Р и имеющей постоянную высоту. Начало координат выберем на свободном конце балки.
Дифференциальное уравнение принимает вид:
Интегрируем два раза:
Для определения постоянных интегрирования имеем условия: точке А при прогиб и угол поворота или
Выражения для у и принимают вид;
Наибольший прогиб на свободном конце балки В получится при : он равен
Если бы мы всю балку сделали постоянного сечения с моментом инерции J, то наибольший прогиб был бы
т. е. в 1 раза меньше.
Таким образом, балки переменного сечения обладают большей гибкостью по сравнению с балками постоянной жесткости при одинаковой с ними прочности. Именно поэтому, а не только ради экономии материала, они и применяются в таких конструкциях, как рессоры.
Читайте также:
