Магнитный поток в металлах
Магнитный поток — величина, характеризующая число магнитных силовых линий поля, проходящих через замкнутый контур.
Майкл Фарадей опытным путем пришел к выводу, что при любом соприкосновении проводника и магнитных линий по проводнику проходит заряд \(\triangle Q\) . Этот заряд прямо пропорционален количеству \( \triangle Ф\) пересеченных линий и обратно пропорционален сопротивлению R контура. Пересечение линий вызывается или движением проводника, или изменением поля.
Позже, представляя замкнутый контур, в котором действует ЭДС индукции, Джеймс Клерк Максвелл подсчитывал количество силовых линий \(\triangle Ф\) , пересекаемых контуром за время \(\triangle t\) . Ф он при этом отождествлял с магнитным потоком сквозь всю поверхность.
В чем измеряется, обозначение и размерность
Единица измерения — вебер, сокращенно Вб. Он обозначается буквой Ф.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Размерность — выражение, демонстрирующее связь физической величины с другими величинами данной системы, разложение ее на сомножители из других величин.
Размерность магнитного потока — \(В \times с = кг \times м^ \times с^ \times А^.\)
От чего зависит величина основного магнитного потока
Его можно изменить следующими способами:
- изменив площадь контура;
- изменив угол его наклона;
- изменив магнитное напряжение.
Чему равен магнитный поток, как найти
Магнитный поток в случае однородного магнитного поля равен произведению модуля индукции В этого поля, площади S плоской поверхности, через которую вычисляется поток, и косинуса угла \(\varphi\) между направлением индукции В и нормали к данной поверхности.
Нормаль — перпендикуляр к плоскости контура.
Также поток можно вычислить через индуктивность, которая пропорциональна отношению полного, или суммарного потока к силе тока.
Обозначение суммарного потока — буква \( \psi\) . Он равен сумме потоков, проходящих через всю поверхность. И в простом случае, где рассматриваются одинаковые потоки, проходящие через одинаковые витки катушки, и в случаях, когда поверхность имеет очень сложную форму, эта пропорциональность сохраняется.
Скорость изменения магнитного потока через контур
Закон электромагнитной индукции Фарадея в интегральном виде выглядит следующим образом:
\(\;\underset С<\oint\;>\;(\overrightarrow\times\;d\overrightarrow l) = - \frac\frac\int \underset S<\int\;>\;(\overrightarrow \times d\overrightarrow).\)
Интеграл в левой части уравнения — циркуляция вектора \(\overrightarrow\) по замкнутому контуру С, это отражает знак интеграла, записанный с кругом. В правой части — скорость изменения потока Ф, который вычисляется как интеграл по поверхности S, «натянутой» на С.
Интеграл — целое, определяемое как сумма его бесконечно малых частей.
Если считать изменение потока в замкнутом контуре равномерным, то закон Фарадея примет следующий вид:
Какой формулой определяется величина магнитного потока
Математически величину Ф описывают двумя формулами:
\(Ф\;=\;\sum_\;\;B\triangle S = B \times S \times \cos\varphi. \)
Связь магнитного потока и работы сил магнитного поля
Герман Гельмгольц первым связал закон Фарадея и закон сохранения энергии. Возьмем проводник с током I, находящийся внутри однородного магнитного поля, которое перпендикулярно плоскости контура, и перемещающийся в нем. Под влиянием силы Ампера F проводник перемещается на отрезок dx. Сила F производит работу dA = IdФ.
Работу источника тока можно измерить, сложив работу на джоулеву теплоту и работу по перемещению проводника внутри поля:
Магнитное поле
Магнитное поле играет очень большую роль в электротехнике и электронике. Без магнитного поля не функционировали бы герконы, электромагнитные реле, соленоиды, катушки индуктивности, дроссели, трансформаторы, двигатели, динамики, генераторы электрической энергии да и вообще много чего.
Природа магнетизма
Согласно одной из легенд, когда-то давным-давно жил в Греции пастух по имени Магнес. И вот шел он как-то со своим стадом овец, присел на камень и обнаружил, что конец его посоха, сделанный из железа, стал притягиваться к этому камню. С тех пор стали называть этот камень магнетит в честь Магнеса. Этот камень представляет из себя оксид железа.

Если такой камень положить на деревянную доску на воду или подвесить на нитке, то он всегда выстраивался в определенном положении. Один его конец всегда показывал на СЕВЕР, а другой — на ЮГ.

Этим свойством камня пользовались древние цивилизации. Поэтому, это был своего рода первый компас. Потом уже стали обтачивать такой камень и делать из разные фигурки. Например, так выглядел китайский древний компас, ложка которого была сделана из того самого магнетита. Ручка у этой ложки всегда показывала на ЮГ.

Ну а далее дело шло за практичностью и маленькими габаритами. Из магнетита вытачивали маленькие стрелки, которые подвешивали на тонкую иглу посередине. Так стали появляться первые малогабаритные компасы.

Древние цивилизации, конечно, не знали еще что такое север и юг. Поэтому, одну сторону магнетита они назвали северным полюсом (North), а противоположный конец — южным (South). Названия на английском очень легко запомнить, если кто смотрел американский мультфильм «Южный парк», он же Сауз (South) парк).

Магнитные линии и магнитный поток
Вокруг магнита экспериментальным путем были обнаружены магнитные силовые линии. Эти магнитные линии создают так называемое магнитное поле.
Как вы могли заметить на рисунке, концентрация магнитных силовых линий на самых краях магнита намного больше, чем в его середине. Это говорит о том, что магнитное поле является более сильным именно на краях магнита, а в его середине практически равна нулю. Направлением магнитных силовых линий считается направление от севера к югу.
Ошибочно считать, что магнитные силовые линии начинают свое движение от северного полюса и заканчивают свой век на южном. Это не так. Магнитные линии — они замкнуты и непрерывны. В магните это будет выглядеть примерно так.

Если приблизить два разноименных полюса, то произойдет притягивание магнитов

Если же приблизить одноименными полюсами, то произойдет их отталкивание

Итак, ниже важные свойства магнитных силовых линий.
- Магнитные линии не поддаются гравитации.
- Никогда не пересекаются между собой.
- Всегда образуют замкнутые петли.
- Имеют определенное направление с севера на юг.
- Чем больше концентрация силовых линий, тем сильнее магнитное поле.
- Слабая концентрация силовых линий указывает на слабое магнитное поле.
Магнитные силовые линии, которые образуют магнитное поле, называют также магнитным потоком.
Итак, давайте рассмотрим два рисунка и ответим себе на вопрос, где плотность магнитного потока будет больше? На рисунке «а» или на рисунке «б»?

Видим, что на рисунке «а» мало силовых магнитных линий, а на рисунке «б» их концентрация намного больше. Отсюда можно сделать вывод, что плотность магнитного потока на рисунке «б» больше, чем на рисунке «а».
В физике формула магнитного потока записывается как

Ф — магнитный поток, Вебер
В — плотность магнитного потока, Тесла
а — угол между перпендикуляром n (чаще его зовут нормалью) и плоскостью S, в градусах
S — площадь, через которую проходит магнитный поток, м 2

Что же такое 1 Вебер? Один вебер — это магнитный поток, который создается полем индукцией 1 Тесла через площадку 1м 2 расположенной перпендикулярно направлению магнитного поля.
Напряженность магнитного поля
Формула напряженности
Слышали ли вы когда-нибудь такое выражение: «напряженность между ними все росла и росла». То есть по сути напряженность — это что-то невидимое, какая-то сдерживающая сила, энергия. Здесь почти все то же самое. Напряженностью магнитного поля также часто называют силой магнитного поля. Напряженность магнитного поля напрямую зависит от плотности магнитного потока и выражается формулой
H — напряженность магнитного поля, Ампер/метр
B — плотность магнитного потока, Тесла
μ0 — магнитная постоянная = 4π × 10 -7 Генри/метр или если написать по человечески 1,2566 × 10 -6 Генри/метр.
Эта формула работает только тогда, когда между витками катушки находится воздух, либо вакуум. Более крутая формула выглядит вот так.
μ — это относительная магнитная проницаемость.
У разных веществ она разная

Напряженность магнитного поля проводника с током
Итак, имеем какой-либо проводник, по которому течет электрический ток.

Для того, чтобы вычислить напряженность магнитного поля на каком-то расстоянии от проводника при условии, что проводник находится в воздушном пространстве либо в вакууме, достаточно воспользоваться формулой
I — сила тока, текущая через проводник, Ампер
r — расстояние до точки, в которой измеряется напряженность, метр
Магнитное поле проводника с током
Оказывается, если через какой-либо проводник пропустить электрический ток, то вокруг проводника образуется магнитное поле.

Здесь можно вспомнить знаменитое правило буравчика, но для наглядности я лучше буду использовать правило самореза, так как почти все хоть раз в жизни ввинчивали либо болт, либо саморез.
Ввинчиваем по часовой стрелке — саморез идет вниз. В нашем случае он показывает направление электрического тока. Движение наших рук показывает направление линий магнитного поля. Все то же самое, когда мы начинаем откручивать саморез. Он начинает вылазить вверх, то есть в нашем случае показывает направление электрического тока, а наша рука в этом время рисует в воздухе направление линий магнитного поля.
Также часто в учебниках физики можно увидеть, что направление электрического тока от нас рисуют кружочком с крестиком, а к нам — кружочком с точкой. В этом случае опять представляем себе саморез и уже в голове увидим направление магнитного поля.

Как думаете, что будет если мы сделаем вот такую петельку из провода? Что изменится в этом случае?

Давайте же рассмотрим этот случай более подробно. Так в этой плоскости оба проводника создают магнитное поле, то по идее они должны отталкиваться друг от друга. Но если они хорошо закреплены, то начинается самое интересное. Давайте рассмотрим вид сверху, как это выглядит.

Как вы можете заметить, в области, где суммируются магнитные силовые линии плотность магнитного потока прям зашкаливает.
Соленоид
А что если сделать много-много таких петелек? Взять какую-нибудь круглую бобину, намотать на нее провод и потом убрать бобину. У нас должно получится что-то типа этого.
Если подать постоянное напряжение на такую катушку, магнитные силовые линии будут выглядеть вот так.

Вы только посмотрите, какая бешеная плотность магнитного потока внутри такой катушки! Получается, что от каждой петельки магнитное поле суммируется, что в итоге дает такую плотность магнитного потока. Такую катушку также называют катушкой индуктивности или соленоидом.
Вот также схема, показывающая как магнитные силовые линии складываются в соленоиде.

Плотность магнитного потока зависит от того, какая сила тока проходит через соленоид. Чтобы увеличить плотность магнитного потока, достаточно поверх витков намотать еще больше витков и вставить сердечник из специального материала — феррита.

Если в электрических цепях есть такое понятие, как ЭДС — электродвижущая сила, то и в магнитных цепях есть свой аналог — МДС — магнитодвижущая сила. Магнитодвижущая сила выражается в виде тока, протекающего через катушку из N витков и выражается в Амперах-витках.

I — это сила тока в катушке, Амперы
N — количество витков катушки, штуки)
Также советую посмотреть очень простое и интересное видео про магнитное поле.
Закон Фарадея или как магнит застревает в медной трубе

Изображение взято с сайта «Популярная механика»
Многие видели опыт с постоянным магнитом, который как бы застревает внутри толстостенной медной трубки. В этой статье будем разбираться в физике процесса.
Сначала запишем формулу магнитного поля постоянного магнита, и посчитаем, какой магнитный поток проходит через поперечное сечение трубы, потом заставим магнитик двигаться и узнаем, какой возникает индуцированный электрический ток в металле, какова рассеиваемая электрическая мощность, запишем и решим уравнение движения постоянного магнита.
И если вы дочитали до этого места и не испугались, добро пожаловать под кат — дальше будет интереснее!
Сам я давно подумывал над тем, чтобы хорошенько разобраться в этом вопросе. И вот недавно зашёл разговор с коллегой по работе. Его ребёнку задали сделать научную демонстрацию в школе, на что папа раздобыл кусок медной трубы и неодим-железо-борный магнит. Ребёнок разобрался, произвёл демонстрацию опыта перед классом, дал пояснения, но ни класс ни учитель особо не впечатлились. На конкурсе научных опытов победил вулкан (!) из соды и лимонной кислоты =) Мы с коллегой прикинули на словах и поняли, что дело ясное, что дело тёмное. Да и в литературе не особо много написано по данной тематике. Этот разговор и сподвиг меня попробовать продраться сквозь дебри. В этой статье пишу, что у меня получилось.
Описание эксперимента
Начнём с просмотра видео с демонстрацией опыта. Прежде чем углубиться в теорию, будет полезно представить картину происходящего в общем. В интернете этот опыт был объяснён и продемонстрирован на видео много раз. Но мне тоже нужно его здесь описать, чтобы далее было понятно, от чего мы отталкиваемся.
Экспериментатор помещает постоянный магнит в виде небольшого шарика в медную трубу, которую он держит вертикально. Вопреки ожиданиям, шарик не падает сквозь трубу с ускорением свободного падения, а движется внутри трубы гораздо медленнее.
Итак, в опыте мы наблюдаем, как постоянный магнит движется внутри полой медной трубы с постоянной скоростью. Зафиксируем произвольную точку в теле медной трубки и мысленно проведем поперечное сечение. Через данное сечение медной трубы проходит магнитный поток, создаваемый постоянным магнитом. Из-за того, что магнит движется вдоль трубы, в сечении проводника возникает переменный магнитный поток, то ли нарастающий, то ли убывающий в зависимости от того, приближается или отдаляется магнит от точки, где мы мысленно провели сечение. Переменный магнитный поток, согласно уравнениям Максвелла, порождает вихревое электрическое поле, вообще говоря, во всём пространстве. Однако, только там, где есть проводник, это электрическое поле приводит в движение свободные заряды, находящиеся в проводнике — возникает круговой электрический ток, который создает уже своё собственное магнитное поле и взаимодействует с магнитным полем движущегося постоянного магнита. Проще говоря, круговой электрический ток создает магнитное поле того же знака, что и постоянный магнит, и на магнит действует некая диссипативная сила, а если конкретно — сила трения. Читатель может справедливо задать вопрос: «Трение чего обо что?» Трение возникает между магнитным полем диполя и проводником. Да, это трение не механическое. Вернее сказать, тела не соприкасаются. Ну и пусть! Трение всё равно есть!
В целом, на словах всё выглядит более или менее складно, а можно ли это описать на языке математики? Приступим…
Математическое описание
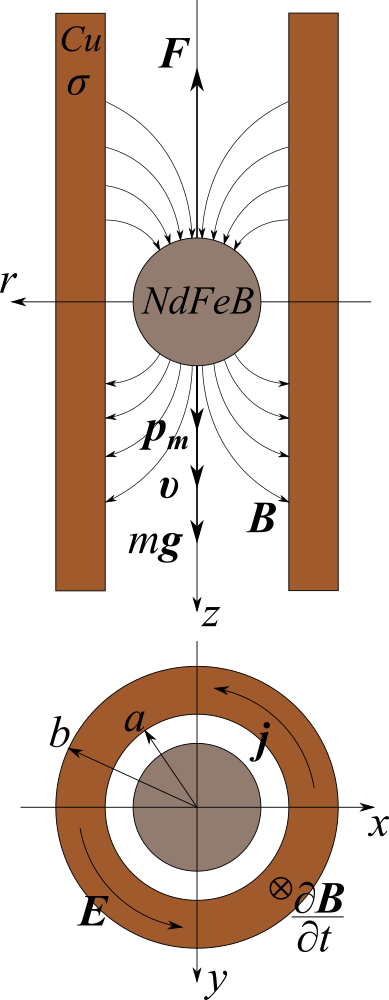
Перво-наперво, нам понадобится математическая модель постоянного магнита. На мой взгляд, будет удобно представить постоянный магнит как магнитный диполь.
Здесь приняты обозначения — радиус-вектор из центра диполя в точку наблюдения, — вектор дипольного момента.
Далее, нам нужно записать -компоненту вектора магнитной индукции для вычисления магнитного потока, захваченного в поперечном сечении металла медной трубы. Выпишем -компоненту магнитного поля здесь
Теперь запишем выражение для магнитного потока через площадь, охватываемую окружностью радиуса на расстоянии от диполя.
Вы не поверите, но этот интеграл берётся. Не буду утомлять. В ответе получается очень красиво
Из-за того, что диполь движется вдоль оси со скоростью , нужно также сделать стандартную подстановку
Похоже, пора призвать на помощь одно из великих уравнений Максвелла, а именно, то самое уравнение, которое описывает закон Фарадея:
Изменение потока магнитной индукции, проходящего через незамкнутую поверхность , взятое с обратным знаком, пропорционально циркуляции электрического поля на замкнутом контуре , который является границей поверхности
Или, что то же самое,
Здесь мы воспользовались аксиальной симметрией задачи по отношению к оси , а также учли, что индуцированное электрическое поле имеет только азимутальную компоненту .
Отсюда можно найти азимутальную компоненту электрического поля, индуцированного магнитом.
Теперь, когда у нас есть выражение для электрического поля, можно вспомнить и о трубе. Как показано на рисунке выше, внутренний радиус трубы равен , а внешний — . Материал трубы — медь. В данный момент нам будет нужна только электрическая проводимость меди. Обозначим проводимость за .
Электрическое поле внутри проводника вызывает электрический ток. Поэтому можем записать закон Ома в дифференциальной форме
Электрический ток, в свою очередь вызывает омические потери внутри проводника. Иными словами, энергия рассеивается внутри проводника и переходит в форму тепла, строго говоря, в нашем случае во всём объёме проводника.
Объёмная плотность мощности омических потерь по определению равна
С другой стороны, при движении магнита сверху вниз потенциальная энергия магнита в поле тяжести Земли уменьшается, однако, скорость движения при этом остаётся постоянной, то есть не растёт, как это бывает при свободном падении. Это означает только одно: потенциальная энергия магнита рассеивается внутри проводника. А с точки зрения сил, действующих на магнит, на него действует сила трения, которая его тормозит и рассеивает потенциальную энергию магнита в тепло.
Запишем теперь баланс мощности в задаче: скорость убывания потенциальной энергии равна мощности омических потерь в проводнике.
Здесь необходимо заметить, что потенциальная энергия в координатах, изображенных на рисунке выше будет равна , а чтобы найти полную мощность омических потерь, следует проинтегрировать по всему объёму проводника. Длину трубы считаем бесконечной. Это не так далеко от истины, если учесть, что в опыте из видеоролика диаметр магнитика много меньше длины трубы.
Последний тройной интеграл выглядит очень сложным. И так оно и есть! Но, во-первых, интегрирование по азимутальному углу можно заменить просто домножением на в силу аксиальной симметрии задачи. Во-вторых, порядок интегрирования в данном конкретном интеграле можно изменить и сначала проинтегрировать по , а уж потом по . В-третьих, при интегрировании по по бесконечным пределам можно смело отбросить слагаемое . Оставшийся интеграл берется машиной.
В итоге получается ответ для полной мощности омических потерь
Здесь после второго знака равенства мы обозначили коэффициент трения
Отметим что, коэффициент трения зависит только от намагниченности магнита , свойств материала проводника и геометрических размеров трубы и — то есть зависит исключительно от параметров магнита и трубы и не зависит от, например, скорости или времени. Это хороший знак для нас и маленький зачётик в копилку найденных формул! Отсюда же становится понятно, почему для демонстрации опыта выбрана именно медная труба, а не, скажем, стальная. Трение зависит от проводимости линейно , а у стали проводимость меньше на порядок.
Это же обстоятельство объясняет и почему магнит левитирует над поверхностью сверхпроводника. Когда мы подносим постоянный магнит к сверхпроводнику, в последнем индуцируются незатухающие внутренние токи, которые создают своё магнитное поле и отталкивают магнитик.
Теперь можно записать
И внезапно (!), перед нами третий закон Ньютона! Сила действия равна силе противодействия. Можем найти установившуюся скорость движения магнита
Уравнение движения
Решать уравнение для неинтересно, потому что ну просто координата меняется с постоянной скоростью. Гораздо полезнее знать, как быстро стабилизируется падение, чему равна установившаяся скорость падения. В общем, надо решать это уравнение для скорости
А решение будет такое
Здесь — коэффициент затухания. Характерное время выхода на установившийся режим падения — . Начальная скорость — , установившаяся скорость — .
А вообще, это уравнение парашютиста. Вот, наверное, почему статья Популярной Механики называется «Магнитный парашют».
Численный эксперимент
А теперь будет то, ради чего всё это затевалось. Навели тут, понимаешь, теорию. А на что она способна? Вдруг это всего лишь как тень на плетень? Или вообще не работает…
Для начала нужно разобраться с геометрией задачи. Видео у нас из MIT, стало быть, американское. Попробую угадать размеры их демонстрационной установки в дюймах (они же в дюймах любят всё измерять). Размер магнитика похож на дюйма в диаметре. Это из тех какие есть в продаже. Тогда масса такого магнитика будет равна примерно г. Размер медной трубы в длину похож на дюймов (1 фут), а внутренний и внешний диаметры трубы, скорее всего, дюйма, дюйма.
С геометрией, вроде разобрались. Теперь физические свойства. Проводимость меди См/м.
Ранее здесь было написано, что я не смог увязать остаточную намагниченность неодимового магнита с его эквивалентным магнитным моментом. Но нашлись добрые люди в комментариях. Пользователь DenisHW подсказал источник (см. п. 5 в списке литературы), где можно прочитать, помог сделать необходимые расчёты и даже проверил их на симуляторе FEMM.

Расчёт магнитного поля шарика из NdFeB на симуляторе FEMM. Изображение предоставлено пользователем DenisHW
Итак, что удалось выяснить. NdFeB магнит относится к классу парамагнетиков, поскольку под воздействием внешнего поля, внутреннее поле усиливается. Более того, сплав NdFeB способен сохранять внутреннее поле после прекращения воздействия внешнего поля. Этот факт классифицирует NdFeB как ферромагнетик. Если обозначить индукцию внутреннего поля магнетика за , а напряжённость внешнего магнитного поля за , то выполняется равенство
Здесь — магнитная восприимчивость вещества, а — вектор намагниченности вещества.
Когда магнит изготавливают на фабрике, его замагничивают внешним полем , а затем внешнее поле отключают, причём магнит сохраняет некоторую остаточную намагниченность . Известно, что для неодимовых магнитов остаточная намагниченность равна примерно Т. Теперь, если исключить внешнее поле из предыдущего уравнения, получится
Откуда находим магнитный момент, приходящийся на единицу объёма материала как
Чтобы найти магнитный момент магнита в целом, нужно умножить на объём шарика
Для остаточной намагниченности Т получается Ам².
Ниже построен график -компоненты магнитного поля в зависимости от радиальной координаты в нашей задаче на расстоянии половины диаметра шарика.

-компонента магнитного поля рядом с поверхностью постоянного магнита
Когда-то доводилось измерять прибором. Поля прямо на поверхности таких магнитов обычно оказываются меньше остаточной намагниченности и составляют порядка нескольких тысяч гаусс. То, что я измерял для прямоугольного магнита, было около 4500 Гс. Поэтому у нас на графике магнитного поля получился вполне реалистичный результат.
Теперь воспользуемся решением уравнения движения, чтобы построить график скорости магнита. Для всех выбранных выше параметров коэффициент трения получается равным Н/(м/с), установившаяся скорость — см/с — как раз примерно 3 дюйма в секунду! На видео шарик проходит через трубу длиной в 12 дюймов примерно за 4 секунды.
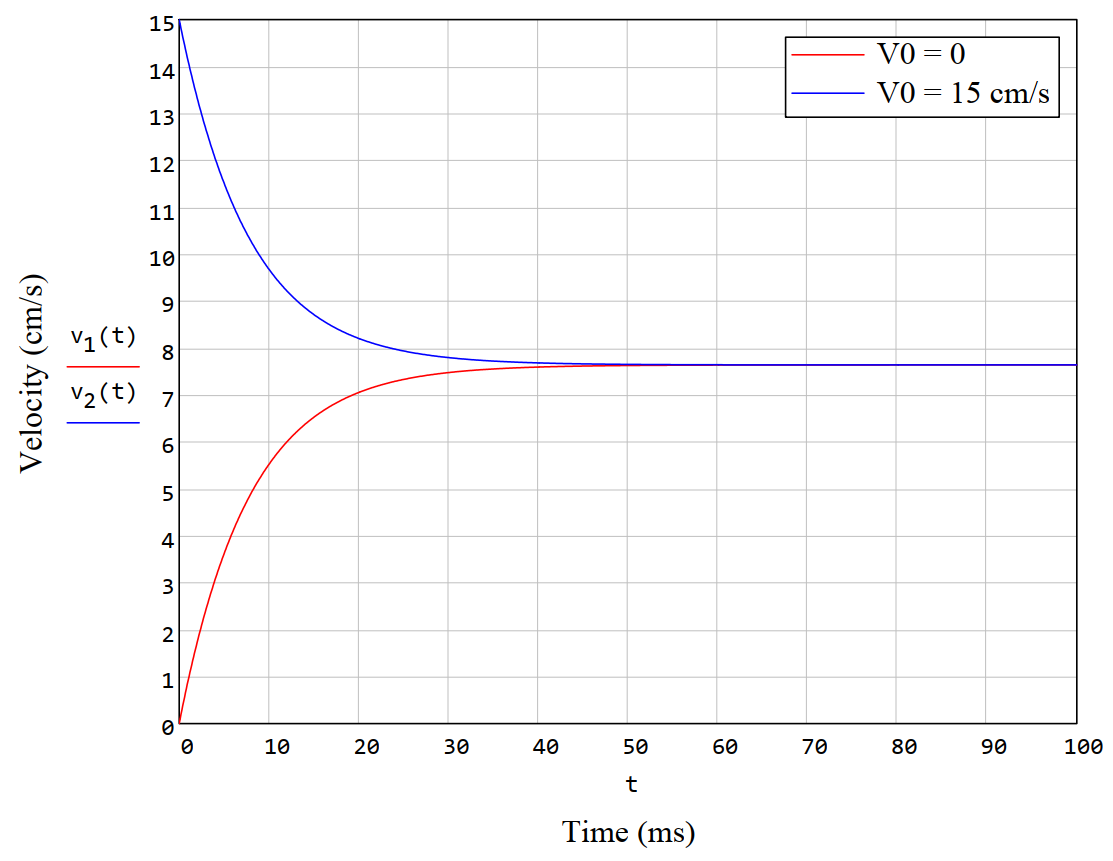
График решения уравнения движения магнитика в медной трубе
А мы продолжаем. Рассеиваемая мощность оказывается равной примерно мВт, а характерное время выхода на установившийся режим — мс. Ниже построены графики для двух разных начальных скоростей: нулевой, и см/с.
И вдобавок, пользователь vashu1 справедливо заметил, что неплохо бы было узнать ток, наведённый в медной трубке. Что ж, и это можно. Проинтегрируем
Интегрировать по нужно именно по полубесконечным пределам, поскольку в другой половине трубы ток течёт в обратном направлении. У меня в ответе получилось А. Честно говоря, я не ожидал, что получится такой большой ток. У пользователя vashu1 получилось 50 А, что, по-видимому, тоже недалеко от действительности. Думаю, vashu1 посчитал сумму токов во всей трубе, что из соображений мощности, тоже разумно.
Вот такое вот получилось исследование. Надеюсь, что было интересно. Оставляйте ваши комментарии. Постараюсь ответить всем. Если вам понравилась статья, поддержите автора лайком или плюсиком в карму. Спасибо, что прочитали.
Магнитная индукция. Определение и описание явления.
Магнитная индукция (обозначается символом В) – главная характеристика магнитного поля (векторная величина ), которая определяет силу воздействия на перемещающийся электрический заряд (ток) в магнитном поле, направленной в перпендикулярном направлении скорости движения.
Магнитная индукция определяется способностью влиять на объект с помощью магнитного поля. Эта способность проявляется при перемещении постоянного магнита в катушке, в результате чего в катушке индуцируется (возникает) ток, при этом магнитный поток в катушке также увеличивается.
Физический смысл магнитной индукции
Физически это явление объясняется следующим образом. Металл имеет кристаллическую структуру (катушка состоит из металла). В кристаллической решетке металла расположены электрические заряды — электроны. Если на металл не оказывать ни какое магнитное воздействие, то заряды (электроны) находятся в покое и никуда не движутся.

Если же металл попадает под действие переменного магнитного поля (из-за перемещения постоянного магнита внутри катушки - именно перемещения), то заряды начинают двигаться под действием этого магнитного поля.
В результате чего в металле возникает электрический ток. Сила этого тока зависит от физических свойств магнита и катушки и скорости перемещения одного относительно другого.
При помещении металлической катушки в магнитное поле заряженные частицы металлический решетки (в кашутке) поворачиваются на определенный угол и размещаются вдоль силовых линий магнитного поля.
Чем выше сила магнитного поля, тем больше количество частиц поворачиваются и тем более однородным будет являться их расположение.
Магнитные поля, ориентированные в одном направлении не нейтрализуют друг друга, а складываются, формируя единое поле.
Формула магнитной индукции
где, В — вектор магнитной индукции, F — максимальная сила действующая на проводник с током, I — сила тока в проводнике, l — длина проводника.
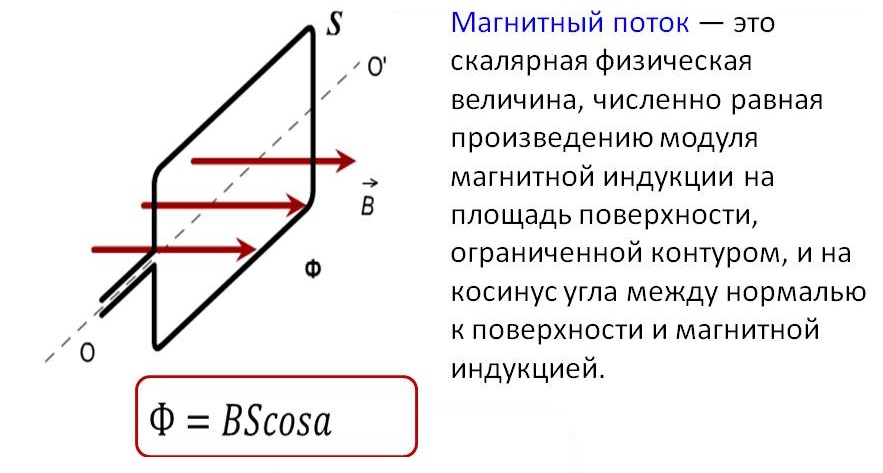
Магнитный поток
Магнитный поток это скалярная величина, которая характеризует действие магнитной индукции на некий металлический контур.
Магнитная индукция определяется числом силовых линий, проходящих через 1 см2 сечения металла.
Магнитометры, используемые для ее измерения, называют теслометрами.

После прекращения движение электронов в катушке сердечник, если он выполнен из мягкого железа, теряет магнитные качества. Если он изготовлен из стали, то он имеет способность некоторое время сохранять свои магнитные свойства.

При построении систем радиосвязи важнейшую роль играют энергетические расчеты радиолиний, или, как говорят, анализ
С энергетической точки зрения электромагнитная волна может рассматриваться как процесс переноса энергии от источника
Так, полностью характеризующий этот процесс, вектор напряженности электрического поля в общем случае описывается тремя

Что такое холостой ход (ХХ) трансформатора? Величина потерь силового трансформатора состоит из так называемых
Наличие гармонических колебаний в электросети – это результат искажения Наличие гармонических колебаний в электросети – это
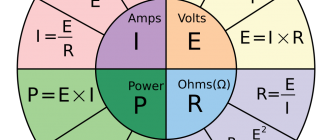
Что такое напряжение в 1 вольт? Напряжение электрического тока – это величина, характеризующая разность
Формулировка «единица силы тока» была впервые употреблена французским математиком и физиком А. Ампером при
Первое упоминание об электричестве встречается в опытах древнегреческого философа Фалеса. Именно он первым обнаружил,


На электростанциях и подстанциях 35-220 кВ и более для питания электроэнергией вспомогательных приборов, агрегатов

Одним из основных параметров периодических и пульсирующих токов выступает частота, определяющая количество периодических колебаний

Частота электрического тока выступает одним из параметров качества электроэнергии и основной характеристикой режима энергосистемы.

Закон Джоуля – Ленца – закон физики, определяющий количественную меру теплового действия электрического тока.
Как образуется электрический ток? Электрический ток появляется в веществе при условии наличия свободных (несвязанных)
Под электрическим напряжением понимают работу, совершаемую электрическим полем для перемещения заряда напряженностью в 1

Своё название щелочные аккумуляторы получили от вида электролита, необходимого для их работы. Основными разновидностями
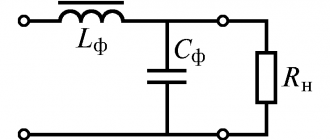
Электрический частотный фильтр необходим в цепи для пропуска лишь желаемого диапазона частот, сигналов в

Определение Амперметр подключается последовательно, с тем участком электроцепи, где предполагается измерять ток. Так как
Ток или поток? Магнитные цепи и их основные характеристики
Привет, Хабр! С недавнего времени я стал задумываться об актуальности статей и заметил, что на Хабре нет ни одной обзорной статьи про магнитные цепи. Как так!? Ведь это. а что это такое?
Действительно, наверняка даже самые отстраненные от инженерного дела люди имеют представление о том, что такое электрические цепи, но возможно, что про магнитные цепи не слышали вовсе. Каждый школьник когда-то в учебнике физики наблюдал разные схемы и формулы, описывающие законы Ома. Но магнитные цепи в рамки школьного курса не входят.
Я решил написать данную статью, чтобы показать, насколько удивителен мир физики и заинтересовать школьников в её изучении. В данной статье, однозначно, для полноты вещей будут и выводы формул и использование некоторых математических операций, которые могут быть известны не всем, но такие моменты я постараюсь сгладить. Приступим.
Что нужно вспомнить?
Для более четкого представления сей статьи, неплохо бы вспомнить основные характеристики самого магнитного поля: вектор магнитной индукции, вектор напряженности, поток вектора магнитной индукции - а также нужно вспомнить немного про магнитные вещества, а именно про ферромагнетики.

Полагается, что вам известен обобщенный закон Ома и помнится, что такое ток, напряжение и сопротивление. Если нет, то крайне советую обратиться к сторонним ресурсам, чтобы иметь хотя бы общее представление о том, что последует далее. Крайне советую учебник И.Е. Иродова «Электромагнетизм».
Применение магнитных цепей
Магнитные цепи находят очень большое поле применения, а именно, они используются для надежного пропускания магнитного потока по специальному проводнику с минимальными или, в некоторых случаях, определенными потерями. В электротехнической промышленности широко используется взаимная зависимость магнитной и электрической энергий, переход из одного состояния в другое. На подобном принципе работают, например, трансформаторы, разные электродвигатели, генераторы и другие устройства.

Конечно, можно продолжительное время говорить об устройствах, разных типах магнитопроводов (про которые речь пойдет далее), но наша первичная цель - рассмотреть выводы основных характеристик магнитных цепей. Продолжаем!
Как устроены магнитные цепи?
Магнитную цепь, на самом деле, не так сложно представить, как может показаться человеку, который о них впервые слышит. Обычно магнитные цепи представляют из себя некоторые фигуры из ферромагнитного сердечника с источником или несколькими источниками ПОтока. Пожалуй, один из самых простых примеров с одним источником, который можно взять на вооружение, проиллюстрирован ниже:
Перед продолжением обусловимся, что среди электротехников сердечник называют магнитопроводом. Часть магнитопровода, на которой отсутствуют обмотки и которая служит для замыкания магнитной цепи, называется «ярмо».
Начнем с тороидального сердечника. Такой тороидальный сердечник может служить формой для катушки, как бы странно это не звучало. Но что за катушка? Ну, первое что приходит в голову - провод, образующий витки. Хорошо, но какого его предназначение? Вернемся к электрическим цепям и вспомним, что существуют источники тока / напряжения, так называемые активные элементы. Так вот, в магнитных цепях роль источника выполняют катушки с током, накрученные на основной элемент магнитной цепи - ферромагнитный магнитопровод.
Вспомним теперь про ферромагнитные материалы. Почему именно они? Дело в том, что благодаря высокому значению магнитной проницаемости, что сигнализирует о хорошей намагниченности ферромагнетика, силовые линии магнитного поля практически не выходят за пределы сердечника, либо не выходят вовсе. Однако это будет справедливо лишь тогда, когда наш сердечник замкнутый, либо имеет небольшие зазоры. То есть, ферромагнетики обладают сильно выраженными магнитными свойствами, когда как у парамагнетиков и диамагнетиков они значительно слабее, что можно наблюдать на следующем графике зависимости намагниченности от напряженности магнитного поля:

Вещества, которые входят в конструкцию магнитопровода, могут обладать не только сильномагнитными свойствами, но также и слабомагнитными. Однако мы рассматриваем сердечник из ферромагнитного материала.
Ещё из школьного курса мы представляем себе картину с линиями магнитной индукции соленоида, мы можем визуально представить его поле и понимаем, что концентрация силовых линий, их насыщенность, наибольшая в центре рассматриваемого соленоида. Тут очень важно вспомнить правило буравчика, чтобы правильно указать направление силовых линий.
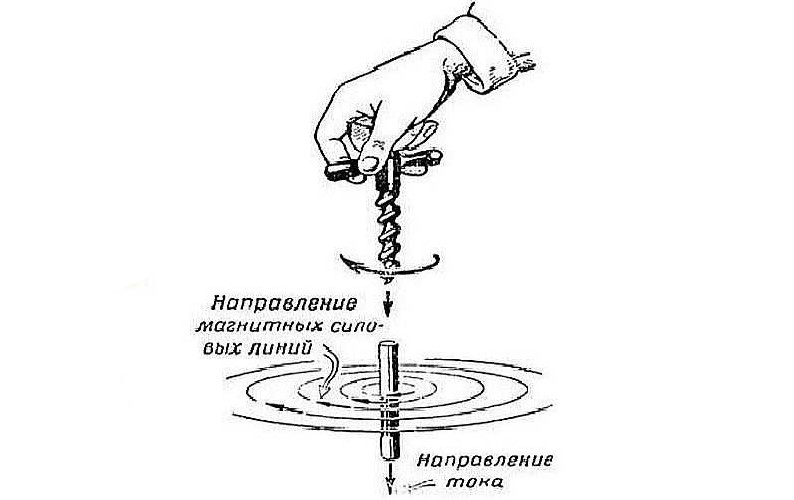
Отсюда становится ясно, что катушки-источники порождают магнитное поле, а следовательно и поток линий магнитной индукции. Такие линии будут циркулировать по нашему сердечнику, словно повторяя его форму. Именно поэтому нам важно условие замкнутости сердечника и материал, из которого он сделан. Положим, что наш воображаемый сердечник замкнут. Из этого следует, что и силовые линии замкнуты, а следовательно выполняется теорема Гаусса для магнитного поля, которая гласит: поток линий магнитной индукции через замкнутую поверхность равен нулю. Стоит учесть, что поток адаптируется под площадь сечения.*

Ну и в конечном счете ферромагнитный сердечник поток куда-то передает! Аналогичным образом замкнутый проводник позволяет передать электрический ток.
Отлично! Мы разобрались с тем, что такое магнитные цепи и даже вспомнили про теорему Гаусса и ферромагнетики. Теперь поговорим о том, какие следствия вытекают из теоремы Гаусса и возможности пренебрежения полем вне сердечника и в зазорах.
1] Магнитные потоки Ф1 и Ф2 через произвольные сечения будут равны между собой.
2] В узле (разветвлении) сердечника алгебраическая сумма потоков (с учетом их направлений) будет равна нулю. Мне одному это что-то напоминает?
То есть мы окончательно сформулировали, что замкнутая (или почти замкнутая) система из ферромагнитных сердечников может рассматриваться как проводящая цепь. В нашем случае - магнитная.
Расчет магнитных цепей
Теперь внимание. Мы можем провести прямую аналогию и рассматривать магнитный поток в цепи, как характеристику электрической цепи - силу тока. Рассмотренное второе следствие означает, что для магнитной цепи, также как и для электрической, справедливо первое правило Кирхгофа. Отсюда можно лаконично перейти к закону полного тока, который в рамках классического магнетизма будет выглядеть следующим образом (приготовьтесь, немного математики):
Криволинейный интеграл по замкнутому контуру от напряженности магнитного поля будет равен алгебраической сумме токов, сцепленных (окруженных) данным контуром.

Также мы помним, что напряженность магнитного поля связана с магнитным потоком следующим образом:
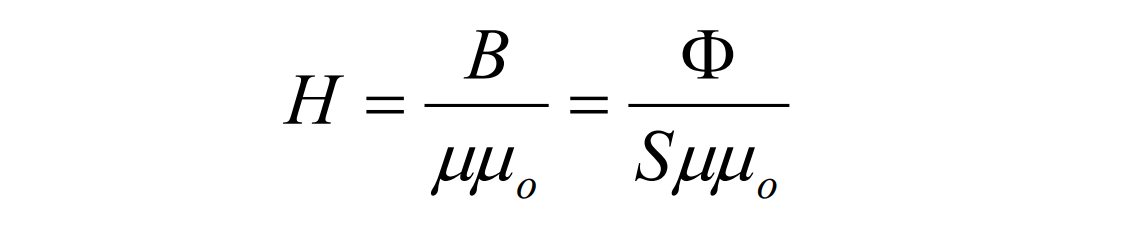
Руководствуясь приведенным законом полного тока и определением напряженности через магнитный поток, мы можем переписать закон полного тока относительно магнитного потока.

Откуда в уравнении появился и что символизирует аргумент l? Все просто. Так как мы рассматриваем контур L, то логично предположить, что на разных его участках наши показатели могут принимать разные значения: площадь сечения может изменяться, как и магнитная проницаемость или магнитный поток.
Полученное уравнение можно рассматривать как второй закон Кирхгофа, который, напомню, звучит следующим образом:
В любой момент времени алгебраическая сумма напряжений на ветвях контура равна нулю.
Для полной ясности, проведем аналогию между электрическими и магнитными цепями, а также их величинами.

Именно проведя аналогичное представление для электрической цепи, мы можем рассчитывать магнитные цепи. Для того, чтобы это сделать, следует:
Мысленно разбить сердечник на отдельные однородные участки (непрерывные, с постоянным сечением) без разветвлений и определить их магнитные сопротивления;
Построить эквивалентную электрическую цепь, последовательно заменяя участки магнитной цепи участками электрической с электрическими сопротивлениями, а также заменяя индуктивности (катушки) на источники ЭДС;
После обозначения заданных сопротивлений и ЭДС, можем вычислить в общем токи в элементах электрической цепи;
Произвести замену полученных величин согласно таблице (токи в потоки, ЭДС в МДС [Магнитодвижущую силу / Ампер-витки], а электрическое сопротивление в магнитное сопротивление).
Именно таким образом, мы можем рассчитать характеристики магнитной цепи. Полученные результаты позволяют, например, вычислить индуктивности.
А примеры расчетов будут?
Здесь - нет. А по ссылке - да! В данном документе Самарского государственного технического университета рассмотрены базовые примеры, которые позволят лучше разобраться в теме, если она вас заинтересовала. Помимо всего прочего, там же приведены теоретические справки. Советую прочитать в надежде, что вы сможете для себя что-то новое подчерпнуть.
Заключение
Во-первых, спасибо, что дочитали статью! Один из способов поддержать меня как автора - подписаться на мой паблик Вконтакте, где иногда выходят «локальные статьи».
Во-вторых, вернемся к началу статьи. Там я задался целью показать, почему физика удивительна. Не хочу быть многословным, поэтому просто попрошу вспомнить все то, что было описано выше. Мы оперировали моделями, которые относятся к разделу физики электричества и перенесли их на физику магнетизма. Наверняка, вы замечали, насколько часто встречаются элементы механики в иных разделах. Это по истине удивительно! Однако главное не поработиться иллюзией, что в мире все законы нам предельно известны.
Читайте также:
