Концентрация электронов в металлах таблица
В начале XX века была создана классическая электронная теория проводимости металлов (П. Друде, 1900 г., Х.Лоренц, 1904 г.), которая дала простое и наглядное объяснение большинства электрических и тепловых свойств металлов.
Рассмотрим некоторые положения этой теории.
Свободные электроны
Металлический проводник состоит из:
1) положительно заряженных ионов, колеблющихся около положения равновесия, и
2) свободных электронов, способных перемещаться по всему объему проводника.
Таким образом, электрические свойства металлов обусловлены наличием в них свободных электронов с концентрацией порядка 10 28 м –3 , что примерно соответствует концентрации атомов. Эти электроны называются электронами проводимости. Они образуются путем отрыва от атомов металлов их валентных электронов. Такие электроны не принадлежат какому-то определенному атому и способны перемещаться по всему объему тела.
В металле в отсутствие электрического поля электроны проводимости хаотически движутся и сталкиваются, чаще всего с ионами кристаллической решетки (рис. 1). Совокупность этих электронов можно приближенно рассматривать как некий электронный газ, подчиняющийся законам идеального газа. Средняя скорость теплового движения электронов при комнатной температуре составляет примерно 10 5 м/с.
Электрический ток в металлах
Ионы кристаллической решетки металла не принимают участие в создании тока. Их перемещение при прохождении тока означало бы перенос вещества вдоль проводника, что не наблюдается. Например, в опытах Э. Рикке (1901 г.) масса и химический состав проводника не изменялся при прохождении тока в течении года.
Экспериментальное доказательство того, что ток в металлах создается свободными электронами, было дано в опытах Л.И. Мандельштама и Н. Д. Папалекси (1912 г., результаты не были опубликованы), а также Т. Стюарта и Р. Толмена (1916 г.). Они обнаружили, что при резкой остановке быстро вращающейся катушки в проводнике катушки возникает электрический ток, создаваемый отрицательно заряженными частицами — электронами.
- электрический ток в металлах — это направленное движением свободных электронов.
Так как электрический ток в металлах образуют свободные электроны, то проводимость металлических проводников называется электронной проводимостью.
Электрический ток в металлах возникает под действием внешнего электрического поля. На электроны проводимости, находящиеся в этом поле, действует электрическая сила, сообщающая им ускорение, направленное в сторону, противоположную вектору напряженности поля. В результате электроны приобретают некоторую добавочную скорость (ее называют дрейфовой). Эта скорость возрастает до тех пор, пока электрон не столкнется с атомом кристаллической решетки металла. При таких столкновениях электроны теряют свою избыточную кинетическую энергию, передавая ее ионам. Затем электроны снова разгоняются электрическим полем, снова тормозятся ионами и т.д. Средняя скорость дрейфа электронов очень мала, около 10 –4 м/с.
- Скорость распространения тока и скорость дрейфа не одно и то же. Скорость распространения тока равна скорости распространения электрического поля в пространстве, т.е. 3⋅10 8 м/с.
- При столкновении с ионами электроны проводимости передают часть кинетической энергии ионам, что приводит к увеличению энергии движения ионов кристаллической решетки, а, следовательно, и к нагреванию проводника.
Сопротивление металлов
Сопротивление металлов объясняется столкновениями электронов проводимости с ионами кристаллической решетки. При этом, очевидно, чем чаще происходят такие столкновения, т. е. чем меньше среднее время свободного пробега электрона между столкновениями τ, тем больше удельное сопротивление металла.
В свою очередь, время τ зависит от расстояния между ионами решетки, амплитуды их колебаний, характера взаимодействия электронов с ионами и скорости теплового движения электронов. С ростом температуры металла амплитуда колебаний ионов и скорость теплового движения электронов увеличиваются. Возрастает и число дефектов кристаллической решетки. Все это приводит к тому, что при увеличении температуры металла столкновения электронов с ионами будут происходить чаще, т.е. время τ уменьшается, а удельное сопротивление металла увеличивается.
См. так же
Зависимость сопротивления от температуры
Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления от температуры выражается линейной функцией:
\(~\rho = \rho_0 \cdot (1 + \alpha \cdot \Delta t),\)
где Δt = t - t0, t0 = 0 °C, ρ0, ρ — удельные сопротивления вещества проводника соответственно при 0 °С и t °C, α — температурный коэффициент сопротивления, измеряемый в СИ в Кельвинах в минус первой степени (К -1 ) (или °C -1 ).
- Температурный коэффициент сопротивления вещества — это величина, численно равная относительному изменению удельного сопротивления проводника при его нагревании на 1 К:
Для всех металлических проводников α > 0 и слабо изменяется с изменением температуры. Для большинства металлов в интервале температур от 0 ° до 100 °С коэффициент α изменяется от 3,3⋅10 –3 до 6,2⋅10 –3 К –1 (таблица 1). У химически чистых металлов α = 1/273 К -1 .
- Существуют специальные сплавы, сопротивление которых практически не изменяется при нагревании, например, манганин и константан. Их температурные коэффициенты сопротивления очень малы и равны соответственно 1⋅10 –5 К –1 и 5⋅10 –5 К –1 .
Температурный коэффициент сопротивления (при t от 0 °С до 100 °C)
| Вещество | α, 10 –3 °К –1 | Вещество | α, 10 –3 °К –1 |
|---|---|---|---|
| Алюминий | 4,2 | Нихром | 0,1 |
| Вольфрам | 4,8 | Олово | 4,4 |
| Железо | 6,0 | Платина | 3,9 |
| Золото | 4,0 | Ртуть | 1,0 |
| Латунь | 0,1 | Свинец | 3,7 |
| Магний | 3,9 | Серебро | 4,1 |
| Медь | 4,3 | Сталь | 4,0 |
| Никель | 6,5 | Цинк | 4,2 |
Если пренебречь изменением размеров металлического проводника при нагревании, то такую же линейную зависимость от температуры будет иметь и его сопротивление
\(~R_t = R_0 \cdot (1 + \alpha \cdot \Delta t) ,\)
где R0, Rt — сопротивления проводника при 0 °С и t °С.
Зависимость удельного сопротивления металлических проводников ρ от температуры t изображена на рисунке 2.

Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве термометрического тела такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры достаточно изучена. Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Сверхпроводимость
В 1911 г. голландский физик Г. Камерлинг-Оннес, изучая изменение электрического сопротивления ртути при низких температурах, обнаружил, что при температуре около 4 К (т.е. при –269 °С) удельное сопротивление скачком уменьшается (рис. 3) до нуля. Это явление Г. Камерлинг-Оннес назвал сверхпроводимостью.

Г. Камерлинг-Оннес был удостоен Нобелевской премии по физике 1913 г. «за исследования свойств вещества при низких температурах».
В дальнейшем было выяснено, что более 25 химических элементов — металлов при очень низких температурах становятся сверхпроводниками. У каждого из них своя критическая температура перехода в состояние с нулевым сопротивлением. Самое низкое значение ее у вольфрама — 0,012 К, самое высокое у ниобия — 9 К.
Сверхпроводимость наблюдается не только у чистых металлов, но и у многих химических соединений и сплавов. При этом сами элементы, входящие в состав сверхпроводящего соединения, могут и не являться сверхпроводниками. Например, NiBi, Au2Bi, PdTe, PtSb и другие.
До 1986 г. были известны сверхпроводники, обладающие этим свойством при очень низких температурах — ниже –259 °С. В 1986-1987 годах были обнаружены материалы с температурой перехода в сверхпроводящее состояние около –173 °С. Это явление получило название высокотемпературной сверхпроводимости, и для его наблюдения можно использовать вместо жидкого гелия жидкий азот.
Широкому применению сверхпроводимости до недавнего времени препятствовали трудности, связанные с необходимостью охлаждения до сверхнизких температур, для чего использовался жидкий гелий. Тем не менее, несмотря на сложность оборудования, дефицитность и дороговизну гелия, с 60-х годов XX века создаются сверхпроводящие магниты без тепловых потерь в их обмотках, что сделало практически возможным получение сильных магнитных полей в сравнительно больших объемах. Именно такие магниты требуются для создания установок управляемого термоядерного синтеза с магнитным удержанием плазмы, для мощных ускорителей заряженных частиц. Сверхпроводники используются в различных измерительных приборах, прежде всего в приборах для измерения очень слабых магнитных полей с высочайшей точностью.
На основе сверхпроводящих пленок создан ряд быстродействующих логических и запоминающих элементов для счетно-решающих устройств. При космических исследованиях перспективно использование сверхпроводящих соленоидов для радиационной защиты космонавтов, стыковки кораблей, их торможения и ориентации, для плазменных ракетных двигателей.
В настоящее время созданы керамические материалы, обладающие сверхпроводимостью при более высокой температуре — свыше 100 К, то есть при температуре выше температуры кипения азота. Возможность охлаждать сверхпроводники жидким азотом, который имеет на порядок более высокую теплоту парообразования, существенно упрощает и удешевляет все криогенное оборудование, обещает огромный экономический эффект.
- Wikipedia Сверхпроводимость
- Буздин А., Варламов А. Страсти по сверхпроводимости в конце тысячелетия //Квант. — 2000. — № 1. — С. 2-8.
- Мякишев Г.Я. Физика: Электродинамика //§2.6. Сверхпроводимость
Недостатки электронной теории проводимости
Несмотря на то, что электронной теории проводимости металлов объяснила ряд явлений, она имеет и свои недостатки.
- Из теории следовало, что удельное сопротивление должно быть пропорционально корню квадратному из температуры (\(~\rho \sim \sqrt T\)), между тем, согласно опыту, ρ ~ Т.
- Для того чтобы получить значения удельной электрической проводимости металла, полученных из опыта, приходится принимать среднюю длину свободного пробега электронов в сотни раз большей, чем период решетки металла. Иными словами, электрон должен проходит без соударений с ионами решетки сотни атомов.
- Данная теория не смогла объяснить причину сверхпроводимости.
Приведенные выше недостатки указывают на то, что классическая электронная теория, представляя электрон как материальную точку, подчиняющуюся законам классической механики, не учитывала некоторых специфических свойств самого электрона, которые еще не были известны к началу XX века. Эти свойства были установлены позднее при изучении строения атома, и в 1924 г. была создана новая, так называемая квантовая или волновая механика движения электронов.
SA. Ток в металлах
И их основные свойства
Проводниками электрического тока в соответствии с терминами и определениями ГОСТ Р 52002-2003 называют вещества, основными электрическими свойствами которых является высокая электропроводность. Их удельное сопротивление при нормальной температуре лежит в пределах от 0,036 до 300 мкОм·м. Эти материалы используют для изготовления токоведущих частей электроустановок. Чаще всего в качестве проводников электрического тока используют твердые тела, реже жидкости и газы в ионизированном состоянии.
Механизм прохождения тока в металлах — как в твердом, так и в жидком состоянии - обусловлен направленным движением (дрейфом) свободных электронов под воздействием электрического поля; поэтому металлы называют проводниками с электронной электропроводностью или проводниками первого рода.
Важнейшими практически применяемыми в электротехнике твердыми проводниковыми материалами являются металлы и их сплавы. Основные свойства металлов приведены в табл 3.3.
Классификация металлических проводников. Металлические проводниковые материалы подразделяются на следующие основные группы:
Металлы высокой проводимости, имеющие удельное сопротивление ρ при нормальной температуре не более 0,05 мкОм∙м, Металлы высокой проводимости используются для изготовления проводов, токопроводящих жил кабелей, обмоток электрических машин и трансформаторов.
Сверхпроводники – это материалы (чистые металлы и сплавы), удельное сопротивление которых при весьма низких температурах, близких к абсолютному нулю скачком уменьшается до ничтожно малой величины.
Высокотемпературные сверхпроводники (ВТСП) – это проводники, имеющие температуру перехода в сверхпроводящее состояние выше 30К.
Криопроводники – это металлические проводники высокой проводимости, удельное сопротивление которых плавно снижается при понижении температуры и при криогенных температурах (Т
Сплавы высокого сопротивления с ρ при нормальной температуре не менее 0,3 мкОм ּ м. Металлы и сплавы высокого сопротивления применяются для изготовления резисторов, электронагревательных приборов, нитей ламп накаливания и т. п.
Металлы и сплавы различного назначения. К ним относятся тугоплавкие и легкоплавкие металлы, а также металлы и сплавы для контактов электрических аппаратов.
Классификация неметаллических проводников. К неметаллическим твердым проводникам относятся:
Угольные материалы - это материалы на основе углерода. Из углеродных материалов изготавливают щетки электрических машин, токосъемные вставки для токоприемников электровозов, электроды для прожекторов и дуговых электрических печей. Угольный порошок применяют в микрофонах.
Композиционные проводящие материалы – это искусственные материалы с электронным характером электрической проводимости, состоящие из проводящей фазы, связующего вещества и заполнителей с высокими диэлектрическими свойствами.
Классификация жидких и газообразных проводников. К жидким проводникам относятся:
Расплавленные металлы. В качестве жидкого металлического проводника при нормальной температуре может быть использована только ртуть (Hg), температура плавления которой около минус 39 °С. Другие металлы могут быть жидкими проводниками только при повышенных температурах, превышающих их температуру плавления.
Электролиты или проводники второго рода - это растворы кислот, щелочей и солей. Электропроводность в электролитах носит ионный характер, так как электрический ток в них обусловлен направленным движением анионов и катионов. Процесс прохождения электрического тока через электролит называют электролизом. В соответствии с законами Фарадея, при прохождении тока через электролиты вместе с переносом электрических зарядов происходит перенос ионов электролита, т. е. ионов проводящего вещества, вследствие чего состав электролита постепенно изменяется, а на электродах выделяются продукты электролиза. Ионные кристаллы в расплавленном состоянии также являются проводниками второго рода.
К газообразным проводникам относятся: все газы и пары, в том числе и пары металлов. При низких напряженностях электрического поля газы являются хорошими диэлектриками. Если же напряженность электрического поля превзойдет некоторое критическое значение, при котором начинается ударная ионизация, то в этом случае газ может стать проводником с электронной и ионной проводимостью. Сильно ионизированный газ при равенстве числа электронов в единице объема числу положительных ионов представляет собой особую проводящую среду, носящую название плазмы.
Газы и пары металлов в качестве проводников используются в газоразрядных лампах освещения. Среди газоразрядных источников оптического излучения наиболее распространены лампы, в которых используется разряд в парах ртути. Это люминесцентные лампы низкого давления (до 0,03МПа) и дуговые ртутные лампы (ДРЛ) высокого давления (0,03-3МПа).
Рассмотрим подробнее механизмы проводимости и основные свойства металлических проводников, наиболее широко применяемых в технике. Они являются основным видом проводниковых материалов в электро- и радиотехнике.
Электропроводность металлов. Твердый металлический проводник представляет собой кристаллическую решетку, в узлах которой расположены положительно заряженные ионы. В пространстве между ионами находятся свободные электроны, которые образуют так называемый электронный газ. Электронный газ и положительные ионы металла, взаимодействуя между собой, образуют прочную металлическую связь. При отсутствии электрического поля свободные электроны, находятся в состоянии хаотического теплового движения, сталкиваясь с колеблющимися атомами кристаллической решетки.
Для электронного газа, как и для обычных газов, используют законы статистики. Рассмотрим основные положения этих законов. Среднее расстояние, проходимое электронами между двумя столкновениями с узлами решетки, называют длиной свободного пробега . Средний промежуток времени между двумя столкновениями называют временем свободного пробега, которое определяют как:
где - средняя скорость теплового движения свободных электронов в металле. При Т=300К средняя скорость =30 5 м/с =300км/с.
Скорости хаотического теплового движения электронов (при определенной температуре) для различных металлов примерно одинаковы. Примерно одинаковы и концентрации свободных электронов n в разных металлах. Поэтому значение удельной проводимости (или удельного сопротивления) в основном зависит лишь от средней длины свободного пробега электронов λ в данном проводнике. Эта длина в свою очередь, определяется структурой проводникового материала. Поэтому все чистые металлы с идеальной кристаллической решеткой характеризуются наименьшими значениями удельного сопротивления; примеси же, искажая кристаллическую решетку, приводят к увеличению ρ.
Если в проводнике существует электрическое поле Е=const, то со стороны этого поля на электроны действует сила . Под действием этой силы электроны приобретают ускорение , пропорциональное напряженности электрического поля E, в результате чего возникает направленное движение электронов. Такое направленное движение называют дрейфом электронов. Скорость направленного движения или дрейфа значительно меньше скорости теплового движения. Во время свободного пробега электроны движутся равноускоренно, приобретая к концу свободного пробега максимальную скорость
где - время свободного пробега.
В конце свободного пробега электрон, сталкиваясь с ионами кристаллической решетки, отдает им приобретенную в электрическом поле энергию, и скорость его становится равной нулю. Следовательно, средняя скорость направленного движения электрона будет равна:
где e=3,602·30 -39 Кл – заряд электрона, m=9,3·30 -33 кг – масса электрона.
Направленное движение электронов создает электрический ток, плотность которого согласно классической теории металлов равна:
Здесь n - концентрация свободных электронов в металле, т. е. число свободных электронов в единице объема металла,
- удельная электрическая проводимость металла, которая тем больше, чем больше концентрация n свободных электронов и средняя длина λ их свободного пробега, См/м (Сименс, деленный на метр),
- удельное электрическое сопротивление – величина, обратная удельной электрической проводимости, Ом∙м (Ом, умноженный на метр).
Удельная проводимость γ не зависит от напряженности электрического поля Е при изменении ее в широких пределах. Уравнение (3.4) представляет собой закон Ома в дифференциальной форме.
Если считать, что концентрация свободных электронов равна концентрации атомов, то эти концентрации можно найти по формуле:
где d- плотность вещества,
NA =6,022·30 23 моль -3 - число Авогадро – число структурных элементов (атомов, молекул, ионов и др.) в единице количества вещества. (моле, равном грамм-атому) ,
A – атомная масса (ранее называлась атомным весом) – масса атома химического элемента, выраженная в атомных единицах массы (а.е.м.). Атомная единица массы равна 3/32 массы изотопа углерода с массовым числом 32 (≈3,6605402·30 -24 г).
При движении свободных электронов в металле под действием электрического поля, они приобретают дополнительную кинетическую энергию, которую отдают узлам кристаллической решетки при столкновении с ними. Отданная энергия превращается в тепловую, в результате чего температура металла повышается. Мощность удельных потерь p, выделяющихся в проводнике и нагревающих его, определяют по закону Джоуля-Ленца, который в дифференциальной форме имеет вид:
Отметим, что при температуре, равной 0 0 К скорость теплового движения электронов будет равна нулю. Они не будут сталкиваться с ионами, находящимися в узлах кристаллической решетки. Длина свободного пробега λ электронов будет равна бесконечности, а удельное сопротивление ρ будет равно нулю (удельная проводимость равна бесконечности). Проводник в этом случае нагреваться не будет.
Пример 3.1 Вычислить концентрацию n свободных электронов в меди при температуре 300К. Плотность меди d=8,94 Мг·/м 3 . Атомная масса меди А=63,54 а.е.м..
Решение. Концентрация свободных электронов в меди находится по формуле:
Здесь NA =6,022·30 23 моль -3 – число Авогадро.
Пример 3.2. В медном проводнике под действием электрического поля проходит электрический ток плотностью . Определить среднюю скорость дрейфа электронов.
Решение. Электрический ток равен количеству зарядов, проходящих за единицу времени через поперечное сечение проводника. Если за время t проходит заряд q, то электрический ток равен: . Заряд q равен: , где e=3,602·30 -39 Кл – заряд электрона, n=8,47·30 28 м -3 – концентрация электронов в меди (см. пример 3.3), V=lS- -объем электронов, проходящих через поперечное сечение S проводника за время t, l – длина объема V электронов, проходящих через поперечное сечение проводника за время t. Следовательно, выражение для тока примет вид:
Здесь - средняя скорость дрейфа электронов.
Пример 3.3. За какое время электрон в проводе линии связи преодолеет расстояние L=3км, если он будет двигаться без столкновения с узлами кристаллической решетки? Разность потенциалов на концах провода U=300В.
Решение. Если электрон будет двигаться без столкновения с узлами кристаллической решетки, то его движение будет равноускоренным и пройденный путь L найдется из выражения: ,
где - ускорение электрона,
e=3,602·30 -39 Кл –заряд электрона,
m=9,33·30 -33 кг – масса покоя электрона.
Пример 3.4.Найти время передачи электрического сигнала по медному проводу длиной L=3км.
Решение. Передача энергии вдоль проводов воздушной линии электропередачи производится электромагнитным полем, которое распространяется вдоль линии со скоростью света с=3·30 8 м/с. Для воздушной линии время передачи сигнала электромагнитным полем будет равно:
Двойственная природа электрона, т.е. свойство корпускулярно-волнового дуализма обусловила то обстоятельство, что движущиеся в металлах свободные электроны (электроны проводимости) следует рассматривать и как корпускулярные частицы, и как частицы, обладающие волновыми свойствами. С этой точки зрения движение электронов в металле – это распространение электромагнитной волны в твердом теле. Сопротивление металла возникает в результате рассеяния этой волны на тепловые колебания кристаллической решетки. Согласно представлениям волновой теории удельное сопротивление металлов также связано с длиной свободного пробега электронов . Это соотношение записывается так:
Здесь h – постоянная Планка.
Исходя из волновой природы электронов, также можно придти к выводу, что чистые металлы обладают наименьшим значением удельного сопротивления. Это связано с тем, что рассеяние электронных волн происходит на дефектах кристаллической решетки, которые соизмеримы с расстоянием порядка четверти длины электронной волны. В металлическом проводнике длина волны электрона порядка –5нм (нанометр=30 -9 м). Дефекты решетки с размерами меньше чем 5/4нм не вызывают заметного рассеяния электромагнитных волн. Дефекты больших размеров вызывают рассеяние энергии, в результате чего электрическое сопротивление увеличивается. В идеальных кристаллах при Т=0 0 К электромагнитные волны должны распространяться без рассеяния и удельное сопротивление ρ должно быть равно нулю. Это значит, что в идеальном кристалле при Е=0К длина свободного пробега электронов стремится к бесконечности. Подтверждением этого положения является тот факт, что сопротивление чистых отожженных металлов стремится к нулю, когда термодинамическая температура приближается к абсолютному нулю. Рассеяние энергии, приводящее к появлению сопротивления, возникает в тех случаях, когда в решетке имеются различные виды нарушения ее правильного строения. Любые неоднородности структуры препятствуют распространению электронных волн и вызывают рост удельного сопротивления материала.
Пример 3.5. Вычислить среднюю длину свободного пробега электрона в меди при Т=300К, если ее удельное сопротивление при этой температуре равно 0,037 мкОм·м, а концентрация свободных электронов в меди n= 8,47·30 28 м -3 .
Решение. Удельное сопротивление металлов связано со средней длиной свободного пробега соотношением: .
Здесь h=6,62·30 -34 Дж·с - постоянная Планка,
e=3,602·30 -39 Кл - заряд электрона.
Отсюда выразим среднюю длину свободного пробега электрона:
Пример 3.6. Сколько электронов пройдет через поперечное сечение проводника за время t=2с, если по проводнику проходит ток I=8А.
Решение. За время t через поперечное сечение проводника проходит заряд q, равный: . Количество электронов:
Здесь e=3,602·30 -39 Кл –заряд электрона,
Основные свойства металлических проводников:К важнейшим параметрам, характеризующим свойства проводниковых материалов, относятся: 3) удельная проводимость γ или обратная ей величина - удельное сопротивление ρ, 2) температурный коэффициент удельного сопротивления ТКρ или αρ, З) коэффициент теплопроводности λТ (ранее его обозначали γT), 4) удельная теплоемкость с; 5) удельная теплота плавления rT ;6) температурный коэффициент линейного расширения ТКЛР; 7) работа выхода электронов из металла А, 8) контактная разность потенциалов и термоэлектродвижущая сила eT (термо-ЭДС.), 9) предел прочности при растяжении σρ и относительное удлинение при разрыве Δl/l.
Связь плотности тока δ, (А/м²), и напряженности электрического поля Е (В/м), в металлическом проводнике, как уже было показано выше, дается известной формулой (3.4) δ = γE, называемой дифференциальной формой закона Ома.
Для проводника, имеющего сопротивление R длину l и постоянное поперечное сечением S, удельное сопротивление ρ вычисляют по формуле
ρ = RS/l. (3.8)
Для измерения ρ проводниковых материалов разрешается пользоваться внесистемной единицей Ом·мм²/м. Связь между названными единицами удельного сопротивления такая:
3 Ом·м = мкОм·м = Ом·мм²/м, т.е. 3Ом·мм 2 /м=3мкОм·м.
Диапазон значений удельного сопротивления ρ металлических проводников при нормальной температуре довольно узок: от 0,036 для серебра и примерно до 3,4 мкОм·м для железохромо-алюминиевых сплавов.
Пример 3.7Проводник длиной L=50 м и диаметром d=0,5мм включен в электрическую цепь. По проводнику проходит ток I=7А, а напряжение на концах проводника U=50В. Определить удельное сопротивление проводника и материал, из которого он изготовлен.
Решение. Из выражения найдем:
Судя по величине удельного сопротивления, провод выполнен из алюминия.
Сопротивление проводника зависит от частоты протекающего по нему тока. Известно, что на высоких частотах плотность тока изменяется по сечению проводника. Она максимальна на поверхности и убывает по мере проникновения вглубь проводника. Происходит вытеснение тока к поверхности проводника. Это явление называют поверхностным эффектом. Он тем сильнее, чем выше частота. Поскольку площадь сечения, через которое протекает ток уменьшилась, то сопротивление провода переменному току стало больше, чем его сопротивление постоянному току. За глубину проникновения тока в проводник на данной частоте принимают глубину, на которой плотность тока уменьшается в е=2,72 раза .по сравнению с ее значением на поверхности проводника.
Пример 3.5. Определить, во сколько раз сопротивление Rf медного провода круглого сечения диаметром d=0,9 мм на частоте f=5МГц больше сопротивления R0 этого провода на постоянном токе.
Решение. Глубина проникновения электромагнитного поля в проводник определяется по формуле:
где - удельное сопротивление меди;
Гн/м –магнитная постоянная;
- относительная магнитная проницаемость меди.
Коэффициент увеличения сопротивления провода круглого сечения определится:
Для случая, когда членом в знаменателе можно пренебречь и формула, упрощаясь, примет вид:
Концентрация электронов в металлах таблица
Электрический ток в металлах – это упорядоченное движение электронов под действием электрического поля.
Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов (опыт Толмена и Стьюарта):

Катушка с большим числом витков тонкой проволоки (рис. 9.1) приводилась в быстрое вращение вокруг своей оси. Концы катушки с помощью гибких проводов были присоединены к чувствительному баллистическому гальванометру.Раскрученная катушка резко тормозилась, и в цепи возникал кратковременных ток, обусловленный инерцией носителей заряда. Полный заряд, протекающий по цепи, измерялся гальванометром.
При торможении вращающейся катушки на каждый носитель заряда e массой m действует тормозящая сила, которая играет роль сторонней силы, то есть силы неэлектрического происхождения:
Сторонняя сила, отнесенная к единице заряда, по определению является напряженностью поля сторонних сил:
Следовательно, в цепи при торможении катушки возникает электродвижущая сила:
За время торможения катушки по цепи протечет заряд q, равный:
где – длина проволоки катушки, I – мгновенное значение силы тока в катушке, R – полное сопротивление цепи, – начальная линейная скорость проволоки.
Хорошая электропроводность металлов объясняется высокой концентрацией свободных электронов, равной по порядку величины числу атомов в единице объема.
Предположение о том, что за электрический ток в металлах ответственны электроны, возникло значительно раньше опытов Толмена и Стюарта. Еще в 1900 году немецкий ученый П. Друде на основе гипотезы о существовании свободных электронов в металлах создал электронную теорию проводимости металлов. Эта теория получила развитие в работах голландского физика Х. Лоренца и носит название классической электронной теории. Согласно этой теории, электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ.
Электронный газ заполняет пространство между ионами, образующими кристаллическую решетку металла. Из-за взаимодействия с ионами электроны могут покинуть металл, лишь преодолев так называемый потенциальный барьер. Высота этого барьера называется работой выхода.
При обычных (комнатных) температурах у электронов не хватает энергии для преодоления потенциального барьера. Согласно теории Друде–Лоренца, электроны обладают такой же средней энергией теплового движения, как и молекулы одноатомного идеального газа. Это позволяет оценить среднюю скорость теплового движения электронов по формулам молекулярно-кинетической теории:
При наложении внешнего электрического поля в металлическом проводнике кроме теплового движения электронов возникает их упорядоченное движение (дрейф), то есть электрический ток. Величина дрейфовой скорости электронов лежит в пределах 0,6 – 6 мм/c. Таким образом, средняя скорость упорядоченного движения электронов в металлических проводниках на много порядков меньше средней скорости их теплового движения.
Малая скорость дрейфа не противоречит опытному факту, что ток во всей цепи постоянного тока устанавливается практически мгновенно. Замыкание цепи вызывает распространение электрического поля со скоростью c = 3·10 8 м/с. Через время (l – длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля и в ней начинается упорядоченное движение электронов.
В классической электронной теории металлов предполагается, что движение электронов подчиняется законам механики Ньютона. В этой теории пренебрегают взаимодействием электронов между собой, а их взаимодействие с положительными ионами сводят только к соударениям. Предполагается также, что при каждом соударении электрон передает решетке всю накопленную в электрическом поле энергию и поэтому после соударения он начинает движение с нулевой дрейфовой скоростью.
Несмотря на то, что все эти допущения являются весьма приближенными, классическая электронная теория качественно объясняет законы электрического тока в металлических проводниках: закон Ома, закон Джоуля – Ленца и объясняет существование электрического сопротивления металлов.
Электрическое сопротивление проводника:
Однако в ряде вопросов классическая электронная теория приводит к выводам, находящимся в противоречии с опытом. Эта теория не может, например, объяснить, почему молярная теплоемкость металлов, также как и молярная теплоемкость диэлектрических кристаллов, равна 3R (закон Дюлонга и Пти). Классическая электронная теория не может также объяснить температурную зависимость удельного сопротивления металлов: теория дает , в то время как из эксперимента получается зависимость ρ ~ T.
Наиболее ярким примером расхождения теории и опытов является сверхпроводимость.
Зонная модель электронной проводимости металлов
Качественное различие между металлами и полупроводниками (диэлектриками) состоит в характере зависимости удельной проводимости от температуры. У металлов с ростом температуры проводимость падает, а у полупроводников и диэлектриков растет. При Т ® 0 К у чистых металлов проводимость s ® ¥. У полупроводников и диэлектриков при Т ® 0 К, s ® 0. Качественного различия между полупроводниками и диэлектриками в отношении электропроводности, нет.
Проявление у одних веществ металлических свойств, а у других полупроводниковых и диэлектрических может быть последовательно объяснено только в рамках квантовой теории.
Согласно квантовым представлениям, энергия электронов в атоме может изменяться дискретным образом. Причем, согласно принципу Паули, в одном квантовом состоянии может находиться не более одного электрона. В результате электроны не собираются на каком-то одном энергетическом уровне, а последовательно заполняют разрешенные энергетические уровни в атоме, формируя его электронные оболочки.
При сближении большого числа атомов и образовании кристаллической структуры химические связи между атомами образуются за счет электронов, находящихся во внешних, валентных, электронных оболочках.
Согласно принципу Паули, атомы не могут сбиться в плотную массу, поскольку в этом случае в одном квантовом состоянии оказалось бы много частиц с полуцелым спином - собственным моментом количества движения (L = ħ/2). Такие частицы называются фермионами, и к ним, в частности, относятся электроны, протоны, нейтроны. Названы они так в честь итальянского физика Э. Ферми, впервые описавшего особенности поведения коллективов таких частиц. При сближении большого числа атомов в пределах твердого тела происходит расщепление исходного энергетического уровня валентного электрона в атоме на N подуровней, где N - число атомов, образующих кристалл. В результате образуется зона разрешенных энергетических уровней для электронов в твердом теле (рис.9.2).

В металлах внешние валентные оболочки заполнены не полностью, например, у атомов серебра во внешней оболочке 5s 1 находится один электрон, в то время как, согласно принципу Паули, могло бы находиться два электрона с различными ориентациями спинов, но второго электрона во внешней оболочке атома серебра просто нет. При сближении N атомов Ag и расщеплении внешнего энергетического уровня 5s 1 1 на N подуровней каждый из них заполняется уже двумя электронами с различными ориентациями спинов. В результате при сближении N атомов серебра возникает энергетическая зона, наполовину заполненная электронами. Энергия, соответствующая последнему заполненному электронному уровню при 0 К, называется энергией Ферми eF≈kTg. Расстояние между соседними энергетическими уровнями DЕ очень мало, поскольку N очень велико, до .
Расстояние между соседними разрешенными уровнями электронов в металлах много меньше энергии теплового движения электронов даже при самых низких температурах. Если поместить проводник в электрическое поле, включив его, например, в замкнутую цепь с источником ЭДС, то электроны начнут перемещаться из точки проводника с меньшим потенциалом к точке с большим потенциалом, так как их заряд отрицателен. Но движение в электрическом поле означает увеличение энергии электрона, а по квантовым представлениям, переход на более высокий энергетический уровень у электрона возможен, если этот соседний уровень свободен. В металлах таких свободных уровней для электронов, находящихся вблизи уровня Ферми, вполне достаточно, поэтому металлы являются хорошими проводниками электрического тока.
Однако эту проводимость обеспечивают не все свободные электроны металла, а лишь те из них, что расположены вблизи уровня Ферми. Концентрация таких электронов примерно равна nT/Tg, где Tg = 5×10 4 К – температура вырождения.
Концентрация электронов и дырок в зонах для различных степеней вырождения электронного или дырочного газа
Распределение электронов и дырок по квантовым состояниям в главных энергетических зонах кристалла. Уровень Ферми. Поверхность Ферми. Плотность квантовых состояний для энергетических зон с изотропным и анизотропным законом дисперсии.
Раздел 4. Статистика равновесных носителей заряда
4.1 Распределение электронов и дырок по квантовым состояниям в главных энергетических зонах кристалла. Уровень Ферми. Поверхность Ферми. Плотность квантовых состояний для энергетических зон с изотропным и анизотропным законом дисперсии.
4.2 Концентрация электронов и дырок в зонах для различных степеней вырождения электронного или дырочного газа.
4.3 Статистика примесных состояний. Функция распределения электронов и дырок по примесным состояниям. Плотность примесных состояний. Примесные зоны. Влияние температуры и концентрации примеси на концентрацию свободных электронов и дырок.
4.4 Плотность квантовых состояний в квантово-размерных структурах с квантовыми ямами, квантовыми нитями и квантовыми точками.
Для определения s твердого тела необходимо знать равновесную (темновую) концентрацию электронов (n) и дырок (p).
Для определения n и p необходимо знать параметры зон – плотность квантовых состояний и вероятность их дополнения – функцию распределения электронов и h + по состояниям.
Функции распределения электронов и дырок по квантовым состояниям разрешения зон (зона проводимости и валентная зона).
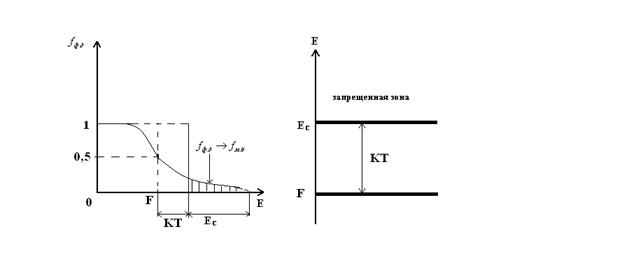
Электроны в металлах, полупроводниках подчиняются квантовой статистике. Вероятность заполнения уровня E при температуре T определяется функцией Ферми – Дирака:Электроны проводимости – фермионы – частицы, обладающие полуцелым спином, и подчиняются принципом Паули:
F – уровень (энергия) Ферми, или электрохимический потенциал.
Основные свойства функции fФ-Д :
При T ® 0При T = 0 функция терпит разрыв (то есть функция не определена).
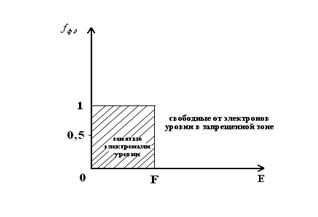
Из графика следует, что f есть уровень, который разделяет занятые электронами состояния в зоне проводимости от свободных.
В металлах при T = 0: уровень F соответствует максимальной энергии электронов в зоне проводимости – энергии Ферми.
Вкоторая соответствует энергии EF.
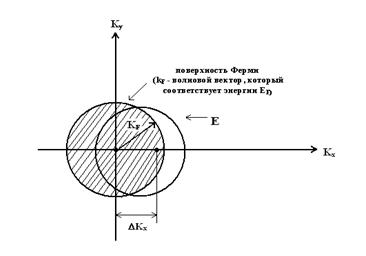
Внутри сферы Ф – находятся электроны проводимости.
Проводимость по зоне проводимости - есть жесткое смещение сферы Ф в - пространстве под действием внешнего электрического поля на величину Dkx.
При температурах T > 0:
fФ-Д = 0,5 и F имеет смысл уровня, вероятность заполнения которого ½.
Функция fФ-Д претерпевает наибольшее изменение для энергий вблизи F.
При (E – F) >> kT функция fФ-Д переходит в классическую функцию Максвелла – Больцмана:
Ф-Д.
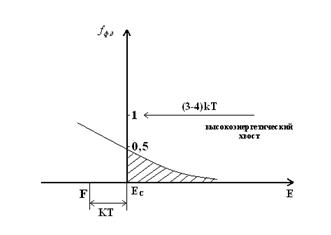
Уровень F ниже Ec на энергию не меньше kT.
В этом случае действует классическая статистика Максвелла – Больцмана и полупроводников, подчиняющиеся этой статистике – невырожденные (по концентрации).
Невырожденный полупроводник n-типа – полупроводник, в котором уровень F лежит ниже Ec в запрещенной зоне на величину не меньше kT.
Таким образом, в невырожденном полупроводнике на уровне f – нет электронов в отличие от металла!
Невырожденный полупроводник p-типа – уровень F лежит выше Ec на величину kT.
Плотность состояний N(E)
- это число квантовых состояний в зоне, приходящихся на единичный интервал энергии в кристалле единичного объема.
Предположим, что в интервале энергии: (E,E + dE) находится dS состояний.
Тогда для кристалла единичного объема: dS = N(E)dE пропорционально dE
N(E) = dS/dE – плотность состояний.
N(E) связана с формой поверхности равной энергии.
Интервалу dE соответствует шаровой слой объема , которым выделяют поверхности равной энергии:
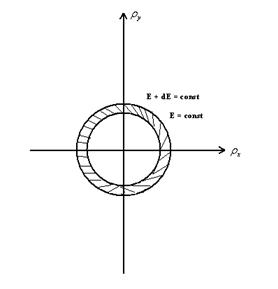
E, E + dE = const
Число состоянийПлотность состояний в зоне проводимости
Эффективная масса – скалярная величина mn
N(E) = dS/dE dS – число состояний в интервале E, E + dE в кристалле единичного объема.
- пространства, заключается между поверхностями равной энергии.
E = const и E +dE = const
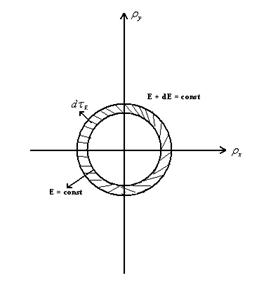
Найдем n
Поверхности E, E + dE заключают объем (поверхности – сферы; Таким образомДля изотропной валентной зоны: (mp – эффективная масса дырки)
Таким образом, плотность состояний пропорциональна:
Зонная модель прямозонного полупроводника с использованием функций N(E)
Используется в физике полупроводниковых приборов.
Плотность состояний в зоне проводимости многодолинного (непрямозонного) полупроводника
Эффективная масса mn - тензорная величина.
Закон дисперсииmC -1 , mU -1 , mZ -1 – компоненты эффективной массы.
Поверхности равной энергии – эллипсоидальные с полуосями.
a, b, c:
Объем эллипсоида: V = 4/3p * a b c
Объем , которым выделяют поверхности E и E + dE = const находят как приращение объема dV.
Таким образом, для одной долины:
Приведем эту формулу к виду для прямозонного полупроводника.
Для этого введем понятие эффективной массы для плотности состояний mnd:
N(E) = 2p (2 mnd / h 2 ) 3/2 (E – Ec) 1/2
Если поверхности – эллипсоиды вращения (электроны в Ge, Si)
m^ и mï½ определяется из эксперимента по циклотронному резонансу.
Смысл введения mnd
Позволяет многодолинную зону проводимости с анизотропной эффективной массой mn записать параболичной зоной с изотропной массой с одним абсолютным минимумом (нужно для вычисления концентраций).
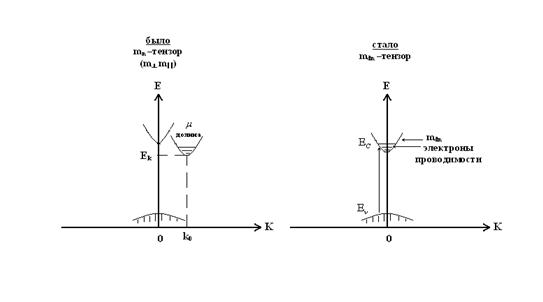
Эффективная масса дырок для плотности состояний - mpd
V1 и V2 – стыкуются в точкеV1 – подзона тяжелых дырок с изотропной массой – mp1
V2 – подзона легких дырок с эффективной массой – mp2.
Плотность состояний для валентной зоны:
эффективная масса дырок для плотности состояний.
Таким образом, с введением mpd сложная V-зона заменяется параболичной невырожденной валентной зоной:
Модель полупроводников с mnd и mpd:
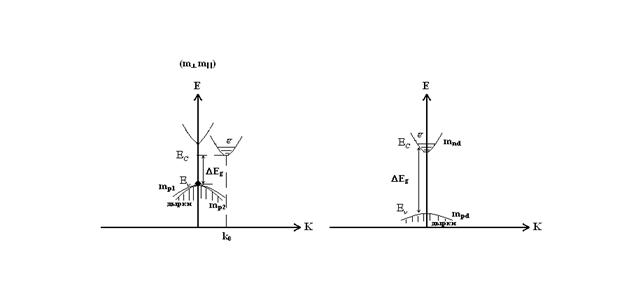
Концентрация электронов и дырок в условиях равновесия в темноте
Концентрация электронов в зоне проводимости.
В интервале E, E + dE в зоне проводимости кристалла единичного объема содержится dn-электронов:
В зоне проводимости: илиВведем новые переменные:
x= E – Ec/ kT – энергия электронов в единичном kT, отсчитывается от дна Ec.
Тогда от параметра Приближенные значениясильновырожденный электронный газ (металлы, вырожденые полупроводники)
Концентрация электронов проводимости в невырожденных полупроводниках
Общая формула: NC – эффективная плотность состояний в зоне проводимости Рассмотрим:dn – число электронов в интервале E, E + dE зоны проводимости для V = 1
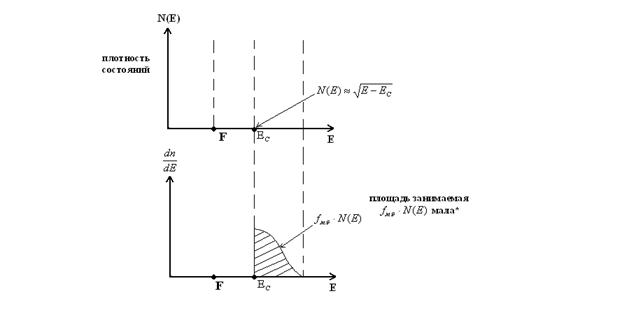
* - это указывает на незначительную концентрацию электронов в зоне проводимости – что характерно для невырожденного полупроводника.
Электроны распределены в узком интервале энергий вблизи дна зоны проводимости.
Электропроводность полупроводника так же зависит по экспоненте от T:
- слабее зависит от T)
Концентрация электронов проводимости в сильновырожденном полупроводнике
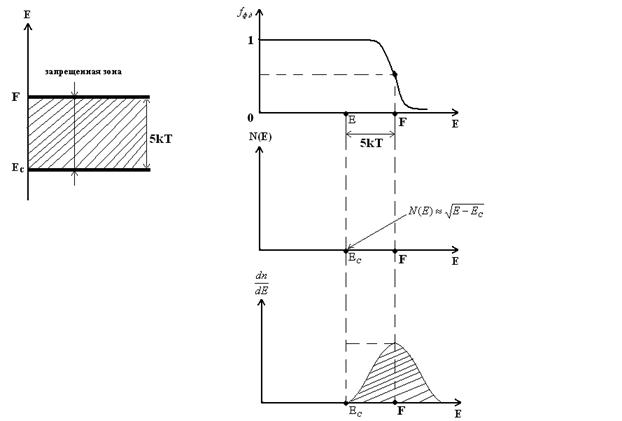
Таким образом, n не зависит от T – признак сильного вырождения электронного газа.
При T = 0 s ¹ 0 (как в металле)
Для промежуточной системы вырождения электронного газа:
Концентрация дырок в полупроводнике p-типа
Невырожденный дырочный газ (полупроводник):Сильно вырожденный дырочный газ (полупроводник):
Сильновырожденный полупроводник p-типа:
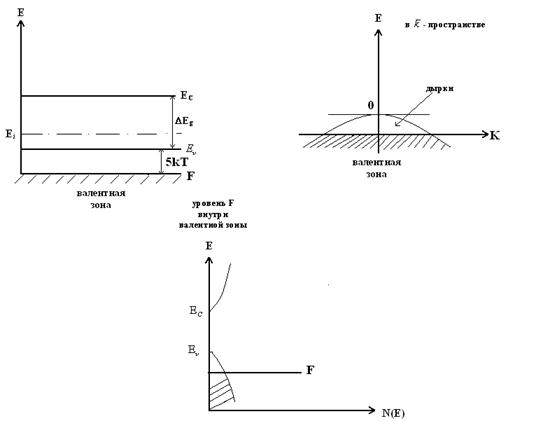
Смысл Nc и Nv в статистике
Таким образом, при расчете n в невырожденном полупроводнике n-типа зону проводимости представляют как набор Nc числа уровней с одинаковой энергией Ec.
Nv – валентная зона состоит из Nv уровней с одинаковой энергией Ev.
Уравнение электрической нейтральности для полупроводников и диэлектриков
Для определения n, p необходимо знать положение уравнения Ферми. Его определяют из уравнения электронейтральности полупроводников (диэлектриков).
Смысл уравнения: в любом физически малом объеме полупроводника (диэлектрика) концентрация отрицательно свободных и связанных зарядов = концентрации свободных и связанных зарядов.
Свободные носители -Связанные: дырки на уровнях донора – концентрация Pd (D + ) электроны – акцептора - na (A - ).
Собственный полупроводник
Уровень Ферми. Собственная концентрация носителей заряда.
G0 и R0 – скорости процессов.
Этому состоянию соответствует равенство n = p = ni
ni – собственная концентрация носителей заряда.
G0 – термическая генерация Энергия рекомбинирующих частиц(Определение Fi
Уравнение электронейтральности: n = p
Для невырожденных собственных полупроводников: Откуда:Fi линейно зависит от T.
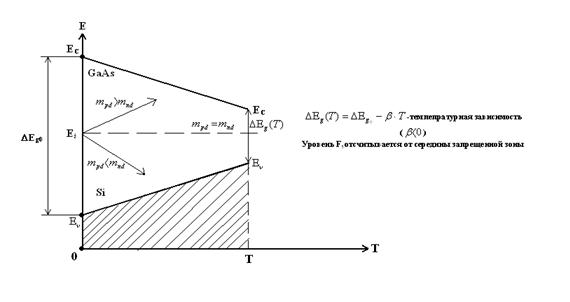
Собственная концентрация ni
ni – зависит от DEg, плотности состояний в зонах и температурах:
.
Угловой коэффициент (
Таким образом, по ni (T) можно определить DEg при T = 0 k.
Произведение np в невырожденном полупроводнике
Используется для определения концентрации неосновных носителей заряда по известной концентрации основных носителей заряда.
Читайте также:
