Количество свободных электронов в металлах
Электрическим током в металлах называют упорядоченное движение электронов под действием электрического поля.
Исходя из опытов, видно, что металлический проводник вещество не переносит, то есть ионы металла не участвуют в передвижении электрического заряда.
Носители тока в металлах
При исследованиях были получены доказательства электронной природы тока в металлах. Еще в 1913 году Л.И. Мандельштам и Н.Д. Папалекси выдали первые качественные результаты. А в 1916 году Р. Толмен и Б. Стюарт модернизировали имеющуюся методику и выполнили количественные измерения, которые доказывали, что движение электронов происходит под действием тока в металлических проводниках.
Рисунок 1 . 12 . 1 показывает схему Толмена и Стюарта. Катушка, состоящая из большого количества витков тонкой проволоки, приводилась в действие при помощи вращения вокруг своей оси. Ее концы были прикреплены к баллистическому гальванометру Г. Производилось резкое торможение катушки, что было следствием возникновения кратковременного тока, обусловленного инерцией носителя заряда. Измерение полного заряда производилось при помощи движения стрелок гальванометра.
Рисунок 1 . 12 . 1 . Схема опыта Толмена и Стюарта.
Во время торможения вращающейся катушки сила F = - m d υ d t , называемая тормозящей, действовала на каждый носитель заряда е . F играла роль сторонней силы, иначе говоря, неэлектрического происхождения. Именно эта сила, характеризующаяся единицей заряда, является напряженностью поля сторонних сил E с т :
E с т = - m e d υ d t .
То есть при торможении катушки происходит возникновение электродвижущей силы δ , равной δ = E с т l = m e d υ d t l , где l – длина проволоки катушки. Определенный промежуток времени процесса торможения катушки обусловлен протеканием по цепи заряда q :
q = ∫ I d t = 1 R ∫ δ d t = m e l υ 0 R .
Данная формула объясняет, что l – это мгновенное значение силы тока в катушке, R – полное сопротивление цепи, υ 0 – начальная линейная скорость проволоки. Видно, что определение удельного заряда e m в металлах производится, исходя из формулы:
Величины, находящиеся с правой стороны, можно измерить. Основываясь на результатах опытов Толмена и Стюарта, установили, что носители свободного заряда имеют отрицательный знак, а отношение носителя в его массе близко по значению удельного заряда электрона, получаемого в других опытах. Было выявлено, что электроны – это носители свободных зарядов.
Современные данные показывают, что модуль заряда электрона, то есть элементарный заряд, равняется e = 1 , 60218 · 10 - 19 К л , а обозначение его удельного заряда – e m = 1 , 75882 · 10 11 К л / к г .
При наличии отличной концентрации свободных электронов есть смысл говорить о хорошей электропроводимости металлов. Это выявили еще перед опытами Толмена и Стюарта. В 1900 году П. Друде, основываясь на гипотезе о существовании свободных электронов в металлах, создал электронную теорию проводимости металлов. Ее развил и расширил Х. Лоренц, после чего она получила название классическая электронная теория. На ее основании поняли, что электроны ведут себя как электронный газ, похожий на идеальный по своему состоянию. Рисунок 1 . 12 . 2 показывает, каким образом он может заполнить пространство между ионами, которые уже образовали кристаллическую решетку металла.
Рисунок 1 . 12 . 2 . Газ свободных электронов в кристаллической решетке металла. Показана траектория одного из электронов.
Потенциальный барьер. Движение электронов в кристаллической решетке
После взаимодействия электронов с ионами первые покидают металл, преодолевая только потенциальный барьер.
Высота такого барьера получила название работы выхода.
Наличие комнатной температуры не позволяет электронам проходить этот барьер. Потенциальная энергия выхода электрона после взаимодействия с кристаллической решеткой намного меньше, чем при удалении электрона из проводника.
Расположение е в проводнике характеризуется наличием потенциальной ямы, глубина которой получила название потенциального барьера.
Ионы, образующие решетку, и электроны принимают участие в тепловом движении. Благодаря тепловым колебаниям ионов вблизи положений равновесий и хаотичному движению свободных электронов, при столкновении первых со вторыми происходит усиление термодинамического равновесия между электронами и решеткой.
По теории Друде-Лоренца имеем, что электроны имеют такую же среднюю энергию теплового движения, как и молекулы одноатомного идеального газа. Это делает возможным оценивание средней скорости υ т ¯ теплового движения электронов, используя молекулярно-кинетическую теорию.
Комнатная температура дает значение, равное 10 5 м / с .
Если наложить внешнее электрическое поле в металлический проводник, тогда произойдет тепловое упорядоченное движения электронов (электрический ток), то есть дрейф. Определение средней его скорости υ д ¯ выполняется по интервалу имеющегося времени ∆ t через поперечное сечение S проводника электронов, которые находятся в объеме S υ д ∆ t .
Количество таких е равняется n S υ д ∆ t , где n принимает значение средней концентрации свободных электронов, равняющейся числу атомов в единице объема металлического проводника. За имеющееся количество времени ∆ t через сечение проводника проходит заряд ∆ q = e n S υ д ∆ t .
Тогда I = ∆ q ∆ t = e n S υ д или υ д = I e n S .
Концентрация n атомов в металлах находится в пределах 10 28 - 10 29 м - 3 .
Формула дает возможность оценить среднюю скорость υ д ¯ упорядоченного движения электронов со значением в промежутке 0 , 6 - 6 м м / с для проводника с сечением 1 м м 2 и проходящим током в 10 А .
Средняя скорость υ д ¯ упорядоченного движения электронов в металлических проводниках на много порядков меньше скорости υ т их теплового движения υ д ≪ υ т .
Рисунок 1 . 12 . 3 демонстрирует характер движения свободного е , находящегося в кристаллической решетке.
Рисунок 1 . 12 . 3 . Движение свободного электрона в кристаллической решетке: а – хаотическое движение электрона в кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным электрическим полем. Масштабы дрейфа υ д ¯ ∆ t сильно преувеличены.
Наличие малой скорости дрейфа не соответствует опыту, когда ток всей цепи постоянного тока устанавливается мгновенно. Замыкание производится при помощи воздействия электрического поля со скоростью c = 3 · 10 8 м / с . По прошествии времени l c ( l - длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля. В ней происходит упорядоченное движение электронов.
Классическая электронная теория металлов предполагает, что их движение подчинено законам механики Ньютона. Данная теория характеризуется тем, что происходит пренебрежение взаимодействием электронов между собой, а взаимодействие с положительными ионами расценивается как соударения, при каждом из которых e сообщает накопленную энергию решетке. Поэтому принято считать, что после соударения движение электрона характеризуется нулевой дрейфовой скоростью.
Абсолютно все выше предложенные допущения приближенные. Это дает возможность объяснения законов электрического тока в металлических проводниках, основываясь на электронной классической теории.
Закон Ома
В промежутке между соударениями на электрон действует сила, равняющаяся по модулю e E , в результате чего получает ускорение e m E .
Конец свободного пробега характеризуется дрейфовой скоростью электрона, которую определяют по формуле
υ д = υ д m a x = e E m τ .
Время свободного пробега обозначается τ . Оно способствует упрощению расчетов для нахождения значения всех электронов. Средняя скорость дрейфа υ д равняется половине максимального значения:
υ д = 1 2 υ д m a x = 1 2 e E m τ .
Если имеется проводник с длиной l , сечением S с концентрацией электронов n , тогда запись нахождения тока в проводнике имеет вид:
I = e n S υ д = 1 2 e 2 τ n S m E = e 2 τ n S 2 m l U .
U = E l – это напряжение на концах проводника. Формула выражает закон Ома для металлического проводника. Тогда электрическое сопротивление необходимо находить:
R = 2 m e 2 n τ l S .
Удельное сопротивление ρ и удельная проводимость ν выражаются как:
ρ = 2 m e 2 n τ ; ν = 1 ρ = e 2 n τ 2 m .
Закон Джоуля-Ленца
Конец пробега электронов под действием поля характеризуется кинетической энергией
1 2 m ( υ д ) m a x 2 = 1 2 e 2 τ 2 m E 2 .
Исходя из предположений, энергия при соударениях передается решетке, а в последствии переходит в тепло.
Время ∆ t каждого электрона испытывается ∆ t τ соударений. Проводник с сечение S и длиной l имеет n S l электронов. Тогда выделившееся тепло в проводнике за ∆ t равняется
∆ Q = n S l ∆ t τ e 2 τ 2 2 m E 2 = n e 2 τ 2 m S l U 2 ∆ t = U 2 R ∆ t .
Данное соотношение выражает закон Джоуля-Ленца.
Благодаря классической теории, имеет место трактовка существования электрического сопротивления металлов, то есть законы Ома и Джоуля-Ленца. Классическая электронная теория не в состоянии ответить на все вопросы.
Она не способна объяснить разницу в значении молярной теплоемкости металлов и диэлектрических кристаллов, равняющейся 3 R , где R записывается как универсальная газовая постоянная. Теплоемкость металла не зависит от количества свободных электронов.
Классическая электронная теория не объясняет температурную зависимость удельного сопротивления металлов. По теории ρ ~ T , а исходя из экспериментов – ρ ~ T . Примером расхождения теории с практикой служит сверхпроводимость.
Сопротивление металлического проводника
Исходя из классической теории, удельное сопротивление металлов должно постепенно уменьшаться при понижении температуры, причем остается конечным при любой T . Данная зависимость характерна для проведения опытов при высоких температурах. Если T достаточно низкая, тогда удельное сопротивление металлов теряет зависимость от температуры и достигает предельного значения.
Особый интерес представило явление сверхпроводимости. В 1911 году его открыл Х. Каммерлинг-Оннес.
Если имеется определенная температура T к р , различная для разных веществ, тогда удельное сопротивление уменьшается до нуля с помощью скачка, как изображено на рисунке 1 . 12 . 4 .
Критической температурой для ртути считается значение 4 , 1 К , для алюминия – 1 , 2 К , для олова – 3 , 7 К . Наличие сверхпроводимости может быть не только у элементов, но и у химических соединений и сплавов. Ниобий с оловом Ni 3 Sn имеют критическую точку температуры в 18 К . Существуют вещества, которые при низкой температуре переходят в сверхпроводящее состояние, тогда как в обычных условиях ими не являются. Серебро и медь являются проводниками, но при понижении температуры сверхпроводниками не становятся.
Рисунок 1 . 12 . 4 . Зависимость удельного сопротивления ρ от абсолютной температуры T при низких температурах: a – нормальный металл; b – сверхпроводник.
Сверхпроводящее состояние говорит об исключительных свойствах вещества. Одним из важнейших является способность на протяжении длительного времени поддерживать электрический ток, возбужденный в сверхпроводящей цепи, без затухания.
Классическая электронная теория не может объяснить сверхпроводимость. Это стало возможным спустя 60 лет после его открытия, основываясь на квантово-механических представлениях.
Рост интереса к данному явлению увеличивался по мере появления новых материалов, способных обладать высокими критическими температурами. В 1986 было обнаружено сложное соединение с температурой T к р = 35 К . На следующий год сумели создать керамику с критической Т в 98 К , которая превышала Т жидкого азота ( 77 К ) .
Явление перехода веществ в сверхпроводящее состояние при Т , превышающих температуру кипения жидкого азота, называют высокотемпературной сверхпроводимостью.
Позже в 1988 году создали Tl - Ca - Ba - Cu - O соединение с критической Т , достигающей 125 К . На данный момент ученые заинтересованы в поиске новых веществ с наиболее высокими значениями T к р . Они рассчитывают на получение сверхпроводящего вещества при комнатной температуре. Если это будет сделано, произойдет революция в науке и технике. До настоящего времени все свойства и механизмы состава сверхпроводимых керамических материалов до конца не исследованы.
Электрический ток в металлах
В этом листке мы приступаем к подробному изучению того, как осуществляется прохождение электрического тока в различных проводящих средах — твёрдых телах, жидкостях и газах.
Напомним, что необходимым условием возникновения тока является наличие в среде достаточно большого количества свободных зарядов, которые могут начать упорядоченное движение под действием электрического поля. Такие среды как раз и называются проводниками электрического тока.
Наиболее широко распространены металлические проводники. Поэтому начинаем мы с вопросов распространения электрического тока в металлах.
Мы много раз говорили о свободных электронах, которые являются носителями свободных зарядов в металлах. Вам хорошо известно, что электрический ток в металлическом проводнике образуется в результате направленного движения свободных электронов.
Свободные электроны
Металлы в твёрдом состоянии имеют кристаллическую структуру: расположение атомов в пространстве характеризуется периодической повторяемостью и образует геометрически правильный рисунок, называемый кристаллической решёткой.
Атомы металлов имеют небольшое число валентных электронов, расположенных на внешней электронной оболочке. Эти валентные электроны слабо связаны с ядром, и атом легко может их потерять.
Когда атомы металла занимают места в кристаллической решётке, валентные электроны покидают свои оболочки — они становятся свободными и отправляются «гулять» по всему кристаллу (а именно, свободные электроны перемещаются по внешним орбиталям соседних атомов. Эти орбитали перекрываются друг с другом вследствие близкого расположения атомов в кристаллической решётке, так что свободные электроны оказываются «общей собственностью» всего кристалла). В узлах кристаллической решётки металла остаются положительные ионы, пространство между которыми заполнено «газом» свободных электронов (рис. 1 ).
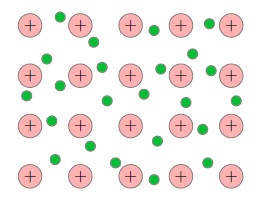
Рис. 1. Свободные электроны
Свободные электроны и впрямь ведут себя подобно частицам газа (другой адекватный образ — электронное море, которое «омывает» кристаллическую решётку) — совершая тепловое движение, они хаотически снуют туда-сюда между ионами кристаллической решётки. Суммарный заряд свободных электронов равен по модулю и противоположен по знаку общему заряду положительных ионов, поэтому металлический проводник в целом оказывается электрически нейтральным.
Газ свободных электронов является «клеем», на котором держится вся кристаллическая структура проводника. Ведь положительные ионы отталкиваются друг от друга, так что кристаллическая решётка, распираемая изнутри мощными кулоновскими силами, могла бы разлететься в разные стороны. Однако в тоже самое время ионы металла притягиваются к обволакивающему их электронному газу и, как ни в чём не бывало, остаются на своих местах, совершая лишь тепловые колебания в узлах кристаллической решётки вблизи положений равновесия.
Что произойдёт, если металлический проводник включить в замкнутую цепь, содержащую источник тока? Свободные электроны продолжают совершать хаотическое тепловое движение, но теперь — под действием возникшего внешнего электрического поля — они вдобавок начнут перемещаться упорядоченно. Это направленное течение электронного газа, накладывающееся на тепловое движение электронов, и есть электрический ток в металле (поэтому свободные электроны называются также электронами проводимости). Скорость упорядоченного движения электронов в металлическом проводнике, как нам уже известно, составляет приблизительно 0,1мм/с.
Опыт Рикке
Почему мы решили, что ток в металлах создаётся движением именно свободных электронов? Положительные ионы кристаллической решётки также испытывают на себе действие внешнего электрического поля. Может, они тоже перемещаются внутри металлического проводника и участвуют в создании тока?
Упорядоченное движение ионов означало бы постепенный перенос вещества вдоль направления электрического тока. Поэтому надо просто пропускать ток по проводнику на протяжении весьма длительного времени и посмотреть, что в итоге получится. Такого рода эксперимент и был поставлен Э.Рикке в 1901 году.
В электрическую цепь были включены три прижатых друг к другу цилиндра: два медных по краям и один алюминиевый между ними (рис. 2 ). По этой цепи пропускался электрический ток в течение года.
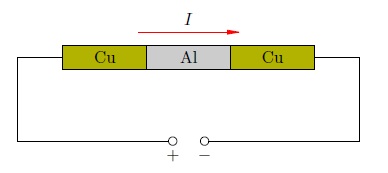
Рис. 2. Опыт Рикке
За год сквозь цилиндры прошёл заряд более трёх миллионов кулон. Предположим, что каждый атом металла теряет по одному валентному электрону, так что заряд иона равен элементарному заряду Кл. Если ток создаётся движением положительных ионов, то нетрудно подсчитать (сделайте это сами!), что такая величина прошедшего по цепи заряда соответствует переносу вдоль цепи около 2кг меди.
Однако после разъединения цилиндров было обнаружено лишь незначительное проникновение металлов друг в друга, обусловленное естественной диффузией их атомов (и не более того). Электрический ток в металлах не сопровождается переносом вещества, поэтому положительные ионы металла не принимают участия в создании тока.
Опыт Стюарта–Толмена
Прямое экспериментальное доказательство того, что электрический ток в металлах создаётся движением свободных электронов, было дано в опыте Т.Стюарта и Р.Толмена (1916 год).
Эксперименту Стюарта–Толмена предшествовали качественные наблюдения, сделанные четырьмя годами ранее русскими физиками Л.И.Мандельштамом и Н.Д.Папалекси. Они обратили внимание на так называемый электроинерционный эффект: если резко затормозить движущийся проводник, то в нём возникает кратковременный импульс тока. Эффект объясняется тем, что в течение небольшого времени после торможения проводника его свободные заряды продолжают двигаться по инерции.
Однако никаких количественных результатов Мандельштам и Папалекси не получили, и наблюдения их опубликованы не были. Честь назвать опыт своим именем принадлежит Стюарту и Толмену, которые не только наблюдали указанный электроинерционный эффект, но и произвели необходимые измерения и расчёты.
Установка Стюарта и Толмена показана на рис. 3 .
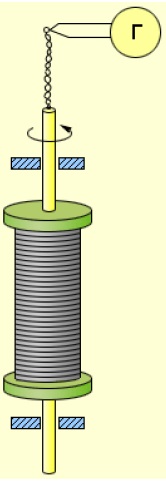
Рис. 3. Опыт Стюарта–Толмена
Катушка большим числом витков металлического провода приводилась в быстрое вращение вокруг своей оси. Концы обмотки с помощью скользящих контактов были подсоединены к специальному прибору — баллистическому гальванометру, который позволяет измерять проходящий через него заряд.
После резкого торможения катушки в цепи возникал импульс тока. Направление тока указывало на то, что он вызван движением отрицательных зарядов. Измеряя баллистическим гальванометром суммарный заряд, проходящий по цепи, Стюарт и Толмен вычислили отношение заряда одной частицы к её массе. Оно оказалось равно отношению для электрона, которое в то время уже было хорошо известно.
Так было окончательно выяснено, что носителями свободных зарядов в металлах являются свободные электроны. Как видите, этот давно и хорошо знакомый вам факт был установлен сравнительно поздно — учитывая, что металлические проводники к тому моменту уже более столетия активно использовались в самых разнообразных экcпериментах по электромагнетизму (сравните, например, с датой открытия закона Ома — 1826 год. Дело, однако, заключается в том, что сам электрон был открыт лишь в 1897 году).
Зависимость сопротивления от температуры
Опыт показывает, что при нагревании металлического проводника его сопротивление увеличивается. Как это объяснить?
Причина проста: с повышением температуры тепловые колебания ионов кристаллической решётки становятся более интенсивными, так что число соударений свободных электронов с ионами возрастает. Чем активнее тепловое движение решётки, тем труднее электронам пробираться сквозь промежутки между ионами (Представьте себе вращающуюся проходную дверь. В каком случае труднее проскочить через неё: когда она вращается медленно или быстро? :-)). Скорость упорядоченного движения электронов уменьшается, поэтому уменьшается и сила тока (при неизменном напряжении). Это и означает увеличение сопротивления.
Как опять-таки показывает опыт, зависимость сопротивления металлического проводника от температуры с хорошей точностью является линейной:
Здесь — сопротивление проводника при . График зависимости (1) является прямой линией (рис. 4 ).
Множитель называется температурным коэффициентом сопротивления. Его значения для различных металлов и сплавов можно найти в таблицах.
Длина проводника и его площадь поперечного сечения при изменении температуры меняются несущественно. Выразим и через удельное сопротивление:
и подставим эти формулы в (1) . Получим аналогичную зависимость удельного сопротивления от температуры:
Коэффициент весьма мал (для меди, например, ), так что температурной зависимостью сопротивления металла часто можно пренебречь. Однако в ряде случаев считаться с ней приходиться. Например, вольфрамовая спираль электрической лампочки раскаляется до такой степени, что её вольт-амперная характеристика оказывается существенно нелинейной.
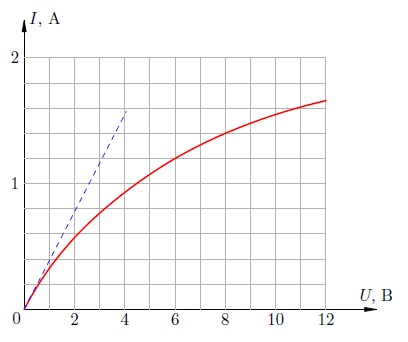
Рис. 5. Вольт-амперная характеристика лампочки
Так, на рис. 5 приведена вольт-амперная характеристика автомобильной лампочки. Если бы лампочка представляла собой идеальный резистор, её вольт-амперная характеристика была прямой линией в соответствии с законом Ома. Эта прямая изображена синим пунктиром.
Однако по мере роста напряжения, приложенного к лампочке, график отклоняется от этой прямой всё сильнее и сильнее. Почему? Дело в том, что с увеличением напряжения ток через лампочку возрастает и больше разогревает спираль; сопротивление спирали поэтому также увеличивается. Следовательно, сила тока хотя и продолжит возрастать, но будет иметь всё меньшее и меньшее значение по сравнению с тем, которое предписывается «пунктирной» линейной зависимостью тока от напряжения.
И их основные свойства
Проводниками электрического тока в соответствии с терминами и определениями ГОСТ Р 52002-2003 называют вещества, основными электрическими свойствами которых является высокая электропроводность. Их удельное сопротивление при нормальной температуре лежит в пределах от 0,036 до 300 мкОм·м. Эти материалы используют для изготовления токоведущих частей электроустановок. Чаще всего в качестве проводников электрического тока используют твердые тела, реже жидкости и газы в ионизированном состоянии.
Механизм прохождения тока в металлах — как в твердом, так и в жидком состоянии - обусловлен направленным движением (дрейфом) свободных электронов под воздействием электрического поля; поэтому металлы называют проводниками с электронной электропроводностью или проводниками первого рода.
Важнейшими практически применяемыми в электротехнике твердыми проводниковыми материалами являются металлы и их сплавы. Основные свойства металлов приведены в табл 3.3.
Классификация металлических проводников. Металлические проводниковые материалы подразделяются на следующие основные группы:
Металлы высокой проводимости, имеющие удельное сопротивление ρ при нормальной температуре не более 0,05 мкОм∙м, Металлы высокой проводимости используются для изготовления проводов, токопроводящих жил кабелей, обмоток электрических машин и трансформаторов.
Сверхпроводники – это материалы (чистые металлы и сплавы), удельное сопротивление которых при весьма низких температурах, близких к абсолютному нулю скачком уменьшается до ничтожно малой величины.
Высокотемпературные сверхпроводники (ВТСП) – это проводники, имеющие температуру перехода в сверхпроводящее состояние выше 30К.
Криопроводники – это металлические проводники высокой проводимости, удельное сопротивление которых плавно снижается при понижении температуры и при криогенных температурах (Т
Сплавы высокого сопротивления с ρ при нормальной температуре не менее 0,3 мкОм ּ м. Металлы и сплавы высокого сопротивления применяются для изготовления резисторов, электронагревательных приборов, нитей ламп накаливания и т. п.
Металлы и сплавы различного назначения. К ним относятся тугоплавкие и легкоплавкие металлы, а также металлы и сплавы для контактов электрических аппаратов.
Классификация неметаллических проводников. К неметаллическим твердым проводникам относятся:
Угольные материалы - это материалы на основе углерода. Из углеродных материалов изготавливают щетки электрических машин, токосъемные вставки для токоприемников электровозов, электроды для прожекторов и дуговых электрических печей. Угольный порошок применяют в микрофонах.
Композиционные проводящие материалы – это искусственные материалы с электронным характером электрической проводимости, состоящие из проводящей фазы, связующего вещества и заполнителей с высокими диэлектрическими свойствами.
Классификация жидких и газообразных проводников. К жидким проводникам относятся:
Расплавленные металлы. В качестве жидкого металлического проводника при нормальной температуре может быть использована только ртуть (Hg), температура плавления которой около минус 39 °С. Другие металлы могут быть жидкими проводниками только при повышенных температурах, превышающих их температуру плавления.
Электролиты или проводники второго рода - это растворы кислот, щелочей и солей. Электропроводность в электролитах носит ионный характер, так как электрический ток в них обусловлен направленным движением анионов и катионов. Процесс прохождения электрического тока через электролит называют электролизом. В соответствии с законами Фарадея, при прохождении тока через электролиты вместе с переносом электрических зарядов происходит перенос ионов электролита, т. е. ионов проводящего вещества, вследствие чего состав электролита постепенно изменяется, а на электродах выделяются продукты электролиза. Ионные кристаллы в расплавленном состоянии также являются проводниками второго рода.
К газообразным проводникам относятся: все газы и пары, в том числе и пары металлов. При низких напряженностях электрического поля газы являются хорошими диэлектриками. Если же напряженность электрического поля превзойдет некоторое критическое значение, при котором начинается ударная ионизация, то в этом случае газ может стать проводником с электронной и ионной проводимостью. Сильно ионизированный газ при равенстве числа электронов в единице объема числу положительных ионов представляет собой особую проводящую среду, носящую название плазмы.
Газы и пары металлов в качестве проводников используются в газоразрядных лампах освещения. Среди газоразрядных источников оптического излучения наиболее распространены лампы, в которых используется разряд в парах ртути. Это люминесцентные лампы низкого давления (до 0,03МПа) и дуговые ртутные лампы (ДРЛ) высокого давления (0,03-3МПа).
Рассмотрим подробнее механизмы проводимости и основные свойства металлических проводников, наиболее широко применяемых в технике. Они являются основным видом проводниковых материалов в электро- и радиотехнике.
Электропроводность металлов. Твердый металлический проводник представляет собой кристаллическую решетку, в узлах которой расположены положительно заряженные ионы. В пространстве между ионами находятся свободные электроны, которые образуют так называемый электронный газ. Электронный газ и положительные ионы металла, взаимодействуя между собой, образуют прочную металлическую связь. При отсутствии электрического поля свободные электроны, находятся в состоянии хаотического теплового движения, сталкиваясь с колеблющимися атомами кристаллической решетки.
Для электронного газа, как и для обычных газов, используют законы статистики. Рассмотрим основные положения этих законов. Среднее расстояние, проходимое электронами между двумя столкновениями с узлами решетки, называют длиной свободного пробега . Средний промежуток времени между двумя столкновениями называют временем свободного пробега, которое определяют как:
где - средняя скорость теплового движения свободных электронов в металле. При Т=300К средняя скорость =30 5 м/с =300км/с.
Скорости хаотического теплового движения электронов (при определенной температуре) для различных металлов примерно одинаковы. Примерно одинаковы и концентрации свободных электронов n в разных металлах. Поэтому значение удельной проводимости (или удельного сопротивления) в основном зависит лишь от средней длины свободного пробега электронов λ в данном проводнике. Эта длина в свою очередь, определяется структурой проводникового материала. Поэтому все чистые металлы с идеальной кристаллической решеткой характеризуются наименьшими значениями удельного сопротивления; примеси же, искажая кристаллическую решетку, приводят к увеличению ρ.
Если в проводнике существует электрическое поле Е=const, то со стороны этого поля на электроны действует сила . Под действием этой силы электроны приобретают ускорение , пропорциональное напряженности электрического поля E, в результате чего возникает направленное движение электронов. Такое направленное движение называют дрейфом электронов. Скорость направленного движения или дрейфа значительно меньше скорости теплового движения. Во время свободного пробега электроны движутся равноускоренно, приобретая к концу свободного пробега максимальную скорость
где - время свободного пробега.
В конце свободного пробега электрон, сталкиваясь с ионами кристаллической решетки, отдает им приобретенную в электрическом поле энергию, и скорость его становится равной нулю. Следовательно, средняя скорость направленного движения электрона будет равна:
где e=3,602·30 -39 Кл – заряд электрона, m=9,3·30 -33 кг – масса электрона.
Направленное движение электронов создает электрический ток, плотность которого согласно классической теории металлов равна:
Здесь n - концентрация свободных электронов в металле, т. е. число свободных электронов в единице объема металла,
- удельная электрическая проводимость металла, которая тем больше, чем больше концентрация n свободных электронов и средняя длина λ их свободного пробега, См/м (Сименс, деленный на метр),
- удельное электрическое сопротивление – величина, обратная удельной электрической проводимости, Ом∙м (Ом, умноженный на метр).
Удельная проводимость γ не зависит от напряженности электрического поля Е при изменении ее в широких пределах. Уравнение (3.4) представляет собой закон Ома в дифференциальной форме.
Если считать, что концентрация свободных электронов равна концентрации атомов, то эти концентрации можно найти по формуле:
где d- плотность вещества,
NA =6,022·30 23 моль -3 - число Авогадро – число структурных элементов (атомов, молекул, ионов и др.) в единице количества вещества. (моле, равном грамм-атому) ,
A – атомная масса (ранее называлась атомным весом) – масса атома химического элемента, выраженная в атомных единицах массы (а.е.м.). Атомная единица массы равна 3/32 массы изотопа углерода с массовым числом 32 (≈3,6605402·30 -24 г).
При движении свободных электронов в металле под действием электрического поля, они приобретают дополнительную кинетическую энергию, которую отдают узлам кристаллической решетки при столкновении с ними. Отданная энергия превращается в тепловую, в результате чего температура металла повышается. Мощность удельных потерь p, выделяющихся в проводнике и нагревающих его, определяют по закону Джоуля-Ленца, который в дифференциальной форме имеет вид:
Отметим, что при температуре, равной 0 0 К скорость теплового движения электронов будет равна нулю. Они не будут сталкиваться с ионами, находящимися в узлах кристаллической решетки. Длина свободного пробега λ электронов будет равна бесконечности, а удельное сопротивление ρ будет равно нулю (удельная проводимость равна бесконечности). Проводник в этом случае нагреваться не будет.
Пример 3.1 Вычислить концентрацию n свободных электронов в меди при температуре 300К. Плотность меди d=8,94 Мг·/м 3 . Атомная масса меди А=63,54 а.е.м..
Решение. Концентрация свободных электронов в меди находится по формуле:
Здесь NA =6,022·30 23 моль -3 – число Авогадро.
Пример 3.2. В медном проводнике под действием электрического поля проходит электрический ток плотностью . Определить среднюю скорость дрейфа электронов.
Решение. Электрический ток равен количеству зарядов, проходящих за единицу времени через поперечное сечение проводника. Если за время t проходит заряд q, то электрический ток равен: . Заряд q равен: , где e=3,602·30 -39 Кл – заряд электрона, n=8,47·30 28 м -3 – концентрация электронов в меди (см. пример 3.3), V=lS- -объем электронов, проходящих через поперечное сечение S проводника за время t, l – длина объема V электронов, проходящих через поперечное сечение проводника за время t. Следовательно, выражение для тока примет вид:
Здесь - средняя скорость дрейфа электронов.
Пример 3.3. За какое время электрон в проводе линии связи преодолеет расстояние L=3км, если он будет двигаться без столкновения с узлами кристаллической решетки? Разность потенциалов на концах провода U=300В.
Решение. Если электрон будет двигаться без столкновения с узлами кристаллической решетки, то его движение будет равноускоренным и пройденный путь L найдется из выражения: ,
где - ускорение электрона,
e=3,602·30 -39 Кл –заряд электрона,
m=9,33·30 -33 кг – масса покоя электрона.
Пример 3.4.Найти время передачи электрического сигнала по медному проводу длиной L=3км.
Решение. Передача энергии вдоль проводов воздушной линии электропередачи производится электромагнитным полем, которое распространяется вдоль линии со скоростью света с=3·30 8 м/с. Для воздушной линии время передачи сигнала электромагнитным полем будет равно:
Двойственная природа электрона, т.е. свойство корпускулярно-волнового дуализма обусловила то обстоятельство, что движущиеся в металлах свободные электроны (электроны проводимости) следует рассматривать и как корпускулярные частицы, и как частицы, обладающие волновыми свойствами. С этой точки зрения движение электронов в металле – это распространение электромагнитной волны в твердом теле. Сопротивление металла возникает в результате рассеяния этой волны на тепловые колебания кристаллической решетки. Согласно представлениям волновой теории удельное сопротивление металлов также связано с длиной свободного пробега электронов . Это соотношение записывается так:
Здесь h – постоянная Планка.
Исходя из волновой природы электронов, также можно придти к выводу, что чистые металлы обладают наименьшим значением удельного сопротивления. Это связано с тем, что рассеяние электронных волн происходит на дефектах кристаллической решетки, которые соизмеримы с расстоянием порядка четверти длины электронной волны. В металлическом проводнике длина волны электрона порядка –5нм (нанометр=30 -9 м). Дефекты решетки с размерами меньше чем 5/4нм не вызывают заметного рассеяния электромагнитных волн. Дефекты больших размеров вызывают рассеяние энергии, в результате чего электрическое сопротивление увеличивается. В идеальных кристаллах при Т=0 0 К электромагнитные волны должны распространяться без рассеяния и удельное сопротивление ρ должно быть равно нулю. Это значит, что в идеальном кристалле при Е=0К длина свободного пробега электронов стремится к бесконечности. Подтверждением этого положения является тот факт, что сопротивление чистых отожженных металлов стремится к нулю, когда термодинамическая температура приближается к абсолютному нулю. Рассеяние энергии, приводящее к появлению сопротивления, возникает в тех случаях, когда в решетке имеются различные виды нарушения ее правильного строения. Любые неоднородности структуры препятствуют распространению электронных волн и вызывают рост удельного сопротивления материала.
Пример 3.5. Вычислить среднюю длину свободного пробега электрона в меди при Т=300К, если ее удельное сопротивление при этой температуре равно 0,037 мкОм·м, а концентрация свободных электронов в меди n= 8,47·30 28 м -3 .
Решение. Удельное сопротивление металлов связано со средней длиной свободного пробега соотношением: .
Здесь h=6,62·30 -34 Дж·с - постоянная Планка,
e=3,602·30 -39 Кл - заряд электрона.
Отсюда выразим среднюю длину свободного пробега электрона:
Пример 3.6. Сколько электронов пройдет через поперечное сечение проводника за время t=2с, если по проводнику проходит ток I=8А.
Решение. За время t через поперечное сечение проводника проходит заряд q, равный: . Количество электронов:
Здесь e=3,602·30 -39 Кл –заряд электрона,
Основные свойства металлических проводников:К важнейшим параметрам, характеризующим свойства проводниковых материалов, относятся: 3) удельная проводимость γ или обратная ей величина - удельное сопротивление ρ, 2) температурный коэффициент удельного сопротивления ТКρ или αρ, З) коэффициент теплопроводности λТ (ранее его обозначали γT), 4) удельная теплоемкость с; 5) удельная теплота плавления rT ;6) температурный коэффициент линейного расширения ТКЛР; 7) работа выхода электронов из металла А, 8) контактная разность потенциалов и термоэлектродвижущая сила eT (термо-ЭДС.), 9) предел прочности при растяжении σρ и относительное удлинение при разрыве Δl/l.
Связь плотности тока δ, (А/м²), и напряженности электрического поля Е (В/м), в металлическом проводнике, как уже было показано выше, дается известной формулой (3.4) δ = γE, называемой дифференциальной формой закона Ома.
Для проводника, имеющего сопротивление R длину l и постоянное поперечное сечением S, удельное сопротивление ρ вычисляют по формуле
ρ = RS/l. (3.8)
Для измерения ρ проводниковых материалов разрешается пользоваться внесистемной единицей Ом·мм²/м. Связь между названными единицами удельного сопротивления такая:
3 Ом·м = мкОм·м = Ом·мм²/м, т.е. 3Ом·мм 2 /м=3мкОм·м.
Диапазон значений удельного сопротивления ρ металлических проводников при нормальной температуре довольно узок: от 0,036 для серебра и примерно до 3,4 мкОм·м для железохромо-алюминиевых сплавов.
Пример 3.7Проводник длиной L=50 м и диаметром d=0,5мм включен в электрическую цепь. По проводнику проходит ток I=7А, а напряжение на концах проводника U=50В. Определить удельное сопротивление проводника и материал, из которого он изготовлен.
Решение. Из выражения найдем:
Судя по величине удельного сопротивления, провод выполнен из алюминия.
Сопротивление проводника зависит от частоты протекающего по нему тока. Известно, что на высоких частотах плотность тока изменяется по сечению проводника. Она максимальна на поверхности и убывает по мере проникновения вглубь проводника. Происходит вытеснение тока к поверхности проводника. Это явление называют поверхностным эффектом. Он тем сильнее, чем выше частота. Поскольку площадь сечения, через которое протекает ток уменьшилась, то сопротивление провода переменному току стало больше, чем его сопротивление постоянному току. За глубину проникновения тока в проводник на данной частоте принимают глубину, на которой плотность тока уменьшается в е=2,72 раза .по сравнению с ее значением на поверхности проводника.
Пример 3.5. Определить, во сколько раз сопротивление Rf медного провода круглого сечения диаметром d=0,9 мм на частоте f=5МГц больше сопротивления R0 этого провода на постоянном токе.
Решение. Глубина проникновения электромагнитного поля в проводник определяется по формуле:
где - удельное сопротивление меди;
Гн/м –магнитная постоянная;
- относительная магнитная проницаемость меди.
Коэффициент увеличения сопротивления провода круглого сечения определится:
Для случая, когда членом в знаменателе можно пренебречь и формула, упрощаясь, примет вид:
Электропроводности металлов. Носителями тока в металлах являются свободные электроны, т
Носителями тока в металлах являются свободные электроны, т. е. электроны, слабо связанные с ионами кристаллической решетки металла. Это представление о природе носителей тока в металлах основывается на электронной теории проводимости метал лов, созданной немецким физиком П. Друде (1863—1906) и разработанной впоследствии нидерландским физиком X. Лоренцем, а также на ряде классических опытов, подтверждающих положения электронной теории.
Первый из таких опытов — опыт Рикке[4] (1901), в котором в течение года электрический ток пропускался через три последовательно соединенных с тщательно отшлифованными торцами металлических цилиндра (Сu, А1, Сu) одинакового радиуса. Несмотря на то, что общий заряд, прошедший через эти цилиндры, достигал огромного значения (»3,5×10 6 Кл), никаких, даже микроскопических, следов переноса вещества не обнаружилось. Это явилось экспериментальным доказательством того, что ионы в металлах не участвуют в переносе электричества, а перенос заряда в металлах осуществляется частицами, которые являются общими для всех металлов. Такими частицами могли быть открытые в 1897 г. английским физиком Д. Томсоном (1856—1940) электроны.
Для доказательства этого предположения необходимо было определить знак и величину удельного заряда носителей (отношение заряда носителя к его массе). Идея подобных опытов заключалась в следующем: если в металле имеются подвижные, слабо связанные с решеткой носители тока, то при резком торможении проводника эти частицы должны по инерции смещаться вперед, как смещаются вперед пассажиры, стоящие в вагоне при его торможении. Результатом смещения зарядов должен быть импульс тока; по направлению тока можно определить знак носителей тока, а зная размеры и сопротивление проводника, можно вычислить удельный заряд носителей. Идея этих опытов (1913) и их качественное воплощение принадлежат российским физикам С. Л. Мандельштаму (1879—1944) и Н. Д. Папалекси (1880—1947). Эти опыты в 1916 г. были усовершенствованы и проведены американским физиком Р. Толменом (1881—1948) и ранее шотландским физиком Б. Стюартом (1828—1887). Ими экспериментально доказано, что носители тока в металлах имеют отрицательный заряд, а их удельный заряд приблизительно одинаков для всех исследованных металлов. По значению удельного заряда носителей электрического тока и по определенному ранее Р. Милликеном элементарному электрическому заряду была определена их масса. Оказалось, что значения удельного заряда и массы носителей тока и электронов, движущихся в вакууме, совпадали. Таким образом, было окончательно доказано, что носителями электрического тока в металлах являются свободные электроны.
Существование свободных электронов в металлах можно объяснить следующим образом: при образовании кристаллической решетки металла (в результате сближения изолированных атомов) валентные электроны, сравнительно слабо связанные с атомными ядрами, отрываются от атомов металла, становятся «свободными» и могут перемещаться по всему объему. Таким образом, в узлах кристаллической решетки располагаются ионы металла, а между ними хаотически движутся свободные электроны, образуя своеобразный электронный газ, обладающий, согласно электронной теории металлов, свойствами идеального газа.
Электроны проводимости при своем движении сталкиваются с ионами решетки, в результате чего устанавливается термодинамическое равновесие между электронным газом и решеткой. По теории Друде — Лоренца, электроны обладают такой же энергией теплового движения, как и молекулы одноатомного газа. Поэтому, применяя выводы молекулярно-кинетической теории (см. (44.3)), можно найти среднюю скорость теплового движения электронов
которая для T=300 К равна 1,1×10 5 м/с. Тепловое движение электронов, являясь хаотическим, не может привести к возникновению тока.
При наложении внешнего электрического поля на металлический проводник кроме теплового движения электронов возникает их упорядоченное движение, т. е. возникает электрический ток. Среднюю скорость ávñ упорядоченного движения электронов можно оценить согласно формуле (96.1) для плотности тока: j = neávñ. Выбрав допустимую плотность тока, например для медных проводов 10 7 А/м 2 , получим, что при концентрации носителей тока n = 8×10 28 м -3 средняя скорость ávñ упорядоченного движения электронов равна 7,8×10 -4 м/с. Следовательно, ávñ ≪ áuñ, т. е. даже при очень больших плотностях тока средняя скорость упорядоченного движения электронов, обусловливающего электрический ток, значительно меньше их скорости теплового движения. Поэтому при вычислениях результирующую скорость (ávñ + áuñ) можно заменять скоростью теплового движения áuñ.
Казалось бы, полученный результат противоречит факту практически мгновенной передачи электрических сигналов на большие расстояния. Дело в том, что замыкание электрической цепи влечет за собой распространение электрического поля со скоростью с (с = 3×10 8 м/с). Через время t = 1/c (l— длина цепи) вдоль цепи установится стационарное электрическое поле и в ней начнется упорядоченное движение электронов. Поэтому электрический ток возникает в цепи практически одновременно с ее замыканием.
Электрический ток в металлах: подробное объяснение
Электрический ток в металлах представляет собой упорядоченное движение свободных электронов. Более подробно об этом читайте далее в нашей статье.
Важно знать
Как известно, электрический ток – это упорядоченный поток носителей электрического заряда. Носители – это заряженные частицы, способные свободно перемещаться во всем объеме тела.
В случае металлов этими частицами являются электроны, которые высвобождаются при образовании связи между атомами металла.
Известно, что металлы в твердом состоянии имеют кристаллическую структуру. Частицы в кристаллах расположены в определенном порядке, образуя пространственную решетку (кристалл).
Наконец, кристаллическая решетка металла образована положительными ионами, погруженными в “облако” хаотически движущихся так называемых свободных электронов, также называемых электронами проводимости. В зависимости от валентности атомов металла, один атом может освободить от одного до трех электронов при образовании металлических связей. Число таких высвобожденных электронов непосредственно переводится в число носителей заряда. Это является одним из факторов, влияющих на способность металла проводить электрический ток.
Доказательством того, что ток в металлах вызывается электронами, послужили эксперименты наших отечественных физиков Леонида Исааковича Мандельштама и Николая Дмитриевича Папалекси, а также американских физиков Бальфура Стюарта и Роберта Толмана.
Способность металла проводить электрический ток может быть описана физической величиной, называемой удельным электрическим сопротивлением. Эта физическая величина обозначается греческой буквой ρ (читается как “ро”). Единицей измерения удельного сопротивления является Ом · м, т.е. произведение Ом на метр. Удельное сопротивление – это константа, которая характеризует материал и имеет различные значения для разных материалов. Например, удельное сопротивление меди составляет 1.72*10 -8 Ом · м. Это означает, что электрическое сопротивление медного проводника длиной 1 метр и площадью поперечного сечения 1 м равно 1.72*10 -8 Ом . В целом, чем ниже удельное сопротивление материала, тем лучше он проводит электрический ток.
В таблице ниже приведены некоторые примеры удельного сопротивления часто используемых металлов.
| Металл | Удельное сопротивление (Ом · м) |
| Серебро | 1.59*10 -8 |
| Медь | 1.72*10 -8 |
| Алюминий | 2.82*10 -8 |
| Вольфрам | 5.6*10 -8 |
| Железо | 10*10 -8 |
Удельное электрическое сопротивление может быть связано с микроскопическими свойствами материала. В частности, он зависит от концентрации носителей заряда и их подвижности.
Движение свободных электронов в металлах не является полностью “свободным”, поскольку во время их движении они взаимодействуют с другими электронами, и прежде всего с ионами кристаллической решетки. Специфика этого движения описывается так называемой классической моделью проводимости.
Основные предположения и выводы этой модели представлены в большом упрощении ниже.
Классическая модель проводимости
Без внешнего электрического поля электроны совершают тепловые хаотические движения, сталкиваясь друг с другом, а также сталкиваясь с ионами кристаллической решетки. В результате такого движения среднее положение электронов практически не меняется (см. рис. 1.).

Рис. 1. Пример траектории электрона во время его хаотического теплового движения в металле
Из-за квантовых эффектов, и в частности из-за принципа запрета Паули, который не позволяет всем электронам занимать самое низкое энергетическое состояние, средняя скорость электронов в металлах, связанная с их хаотическим тепловым движением, больше, чем скорость частиц в классическом идеальном газе той же температуры. Она составляет порядка 10 м/с.
Если электрическое напряжение U приложено к концам проводника длиной L в нем появится электрическое поле с напряженностью E = U / L
Под действием этого внешнего поля, согласно второму закону динамики, электроны ускоряются: a = F / m,
где F = e*E – сила, с которой электрическое поле действует на электрон с зарядом e. Таким образом, ускорение электрона составляет: a = e*E / m .
Ускоренное движение электрона длится лишь довольно короткое время, пока он не столкнется с ионом
кристаллической решетки. В результате такого столкновения электрон теряет практически всю свою кинетическую энергию. Однако замедленный электрон не остается в состоянии покоя – он снова ускоряется под действием электрического поля, снова сталкивается с одним из ионов из ионы кристаллической решетки и т.д. Этот эффект добавляет к скорости тепловых движений дополнительную направленную среднюю скорость u, которая из-за отрицательного заряда электрона имеет направление, противоположное напряженности внешнего электрического поля. Эта скорость называется средней скоростью дрейфа (рис. 2).

Рис. 2. Дрейф электрона под действием внешнего электрического поля
В проводнике начинает течь электрический ток с силой тока I (см. рисунок 3).

Рис. 3. Дрейфующие электроны сталкиваются с ионами кристаллической решетки
Предполагая, что движение электрона равномерно ускоряется между столкновениями с ионами решетки, с ускорением a = e*E / m , и предполагая, что в результате столкновения электрон передает всю свою кинетическую энергию кристаллической решетке, мы можем вычислить скорость, которую развивает электрон в своем свободном движении: v = a*τ . В этой формуле τ – средний интервал времени между последующими столкновениями дрейфующего электрона с ионами кристаллической решетки.
Поскольку при равномерно ускоренном движении без начальной скорости средняя скорость является средним арифметическим начальной (равной нулю) и конечной скоростью, то получаем: u = v / 2 = e*E*τ / 2*m .
Из полученной формулы следует, что скорость дрейфа, помимо внешнего электрического поля, определяется средним интервалом времени между столкновениями электронов с ионами решетки. Этот параметр зависит от многих факторов (включая температуру, кристаллическую структуру металла, дефекты кристаллической структуры, примеси) и, как выясняется, существенно влияет на электрическое сопротивление материала.
Средняя дрейфовая скорость электронов составляет порядка 10 -4 м/с. Она очень мала по сравнению со скоростью теплового движения, которая составляет порядка 10 6 м/с.
Классическая теория проводимости достаточно хорошо описывает явление электропроводности в металлах. Однако эта теория не может объяснить экспериментально наблюдаемую зависимость электрического сопротивления от температуры.
Причина упомянутой неудачи классической теории проводимости заключается в том, что она не учитывает влияние ионов решетки на движение электронов между столкновениями. Более близкие к реальности результаты дает квантовая теория проводимости, которая описывает электроны как частицы, подверженные квантовой статистике, движущиеся в периодическом электрическом поле, создаваемом положительными ионами решетки.
Выводы простым языком
Отрицательный заряд всех свободных электронов по абсолютному значению равен положительному заряду всех ионов решётки. Поэтому в обычных условиях металл электрически нейтрален. Свободные электроны в нём движутся беспорядочно. Но если в металле создать электрическое поле, то свободные электроны начнут двигаться направленно под действием электрических сил. Возникнет электрический ток. Беспорядочное движение электронов при этом сохраняется, подобно тому как сохраняется беспорядочное движение в стайке мошкары, когда под действием ветра она перемещается в одном направлении.
« Скорость движения самих электронов в проводнике под действием электрического поля невелика – несколько миллиметров в секунду, а иногда и ещё меньше. Но как только в проводнике возникает электрическое поле, оно с огромной скоростью, близкой к скорости света в вакууме (300 000 км/c), распространяетcя по всей длине проводника. »
Перышкин А. В. Физика 8. – М.: Дрофа, 2010
Как пример, электрический сигнал, посланный, например, по проводам из Москвы во Владивосток (s = 8000 км), приходит туда примерно через 0,03 с.
Одновременно с распространением электрического поля все электроны начинают двигаться в одном направлении по всей длине проводника. Так, например, когда цепь электрической лампы замкнута, электроны в спирали лампы также движутся упорядоченно.
Сравнение электрического тока с потоком воды в водопроводной системе и распространения электрического поля с распространением давления воды поможет нам понять это. Когда вода поднимается в резервуар для воды, давление (напор) воды очень быстро распространяется по всей системе водоснабжения. Когда мы включаем кран, вода уже находится под давлением и сразу же начинает течь. Но вода, которая была в кране, течет, а вода из башни достигает крана гораздо позже, потому что вода движется с меньшей скоростью, чем распространяется давление.
Когда говорят о скорости распространения электрического тока в проводнике, то имеют в виду скорость распространения по проводнику электрического поля.
Читайте также:
