Коэффициент теплопередачи металл вода
Конвективный теплообмен — обмен теплотой между частями жидкости (газа), имеющими разную температуру или между жидкостью (газом) и твердым телом. Конвективный теплообмен между жидкостью и твердым телом называют теплоотдачей.
Коэффициентом теплоотдачи называется физическая величина, которая характеризует интенсивность теплоотдачи при известном изменении температуры.
Этот коэффициент часто используют в гидроаэродинамике, когда исследуют конвективный теплообмен. Часто ее обозначают буквой . Коэффициент равен:
где — плотность теплового потока, — температурный напор. Величина q — это количество теплоты, которое передается через единичную площадь поверхности тела в единицу времени. находят как модуль разности температур жидкости и поверхности тела. Иногда температурный напор находят, например, в случае обтекания тела потоком сжимаемой жидкостью, считают равным модулю разности температуры жидкости далеко от тела и температурой поверхности тела, которая была бы в отсутствии теплообмена.
Коэффициент теплоотдачи зависит от скорости потока носителя тепла, вида течения, какова геометрия поверхности твердого тела и т.д. Это сложная величина и ее невозможно определить общей формулой. Обычно коэффициент теплоотдачи находят экспериментально.
Так, для условий свободной конвекции воздуха: (Вт/м 2 К), воды: (Вт/м 2 К). При вынужденной конвекции величины коэффициента теплоотдачи колеблются в пределах: для воздуха: (Вт/м 2 К), для воды: (Вт/м 2 К).
Формула Ньютона-Рихмана
Коэффициент теплоотдачи входит в выражение для потока тепла в веществе жидкой или газообразной среды с интенсивным изменением температуры при увеличении расстояния от охлаждаемого или нагреваемого объекта:
![\[Q=\alpha \left(T_{sr}-T_{pov}\right)S\left(2\right),\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e78347c3ffda2b7551186d73f04be855_l3.png)
где — количество теплоты, которая отводится от поверхности, имеющую площадь S, — температура вещества (жидкости, газа), — температура поверхности тела. Выражение (2) называется формулой Ньютона — Рихмана.
Так как интенсивность теплообмена может изменяться при передвижении вдоль площади соприкосновения жидкого носителя с поверхностью твердого тела, вводят местный коэффициент теплоотдачи, который равен:
![\[\alpha =\frac{dQ}{\left(T_{sr}-T_{pov}\right)dS}=\frac{q}{T_{sr}-T_{pov}}(3)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-05b3206da545868f7f177a216cabc1b1_l3.png)
На практике чаще применяют средний коэффициент теплоотдачи , вычисляя его по формуле:
![\[\left\langle \alpha \right\rangle =\frac{Q}{\left(T_{sr}-T_{pov}\right)S}\left(4\right),\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1e4ab352bb8667230a610cb6ce7e2119_l3.png)
где температуры берут средние для поверхности и для вещества.
Дифференциальное уравнение теплоотдачи
Дифференциальное уравнение теплоотдачи показывает связь между коэффициентом теплоотдачи и полем температур среды (жидкости или газа):
![\[\alpha =-\frac{\varkappa }{\Delta T}{\left(\frac{\partial T}{\partial n}\right)}_{n=0}\left(5\right),\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-87f37ed71925ac78c833a680a43b022b_l3.png)
где , — градиент температуры, индекс n=0 значит то, что градиент берут на стенке.
Критерий Нуссельта
Критерий Нуссельта ( ) является характеристикой теплообмена на границе между жидкостью и стеной:
где — характерный линейный размер, — коэффициент теплопроводности жидкости. Для стационарного процесса критерий Нуссельта находят, используя критериальное уравнение конвективного теплообмена:
![\[Nu=A\cdot {Re}^n{Pr}^m{Gr}^k\left(6\right),\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d4f3e77ba2dccf9158a0679400981737_l3.png)
где постоянные. — критерий Рейнольдса, — критерий Прандтля, — критерий Грасгофа.
Коэффициент теплоотдачи и его связь с коэффициентом теплопередачи
Коэффициентом теплопередачи через плоскую стенку связан с коэффициентами теплоотдачи выражением:
где — коэффициент теплоотдачи от первой среды к стенке, — коэффициент теплоотдачи от стенки ко второй среде, — толщина стенки, — коэффициент теплопроводности стенки.
Единицы измерения
Основной единицей измерения коэффициента теплоотдачи в системе СИ является:
=Вт/м 2 К
Примеры решения задач
| Задание | Вычислите тепловой поток, который передается от воды к стенке трубы горизонтального трубчатого радиатора, если средний коэффициент теплоотдачи равен Вт/м 2 К, внутренний диаметр трубы равен м, длина трубы м. Средняя температура воды в трубе по длине равна 80 o C, температура внутренней стенке трубы |
| Решение | За основу решения задачи примем выражение: |
![\[Q=\left\langle \alpha \right\rangle \left(T_{sr}-T_{pov}\right)S\left(1.1\right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-fd97476cb99cc877e693ab3650fa7324_l3.png)
Площадь поверхности трубы найдем как площадь боковой поверхности цилиндра:
Теплопроводность чистых металлов

Теплопроводность металлов в зависимости от температуры
В таблице представлена теплопроводность металлов в зависимости от температуры при отрицательных и положительных температурах (в интервале от -200 до 2400°C).
Таблица теплопроводности металлов содержит значения теплопроводности следующих чистых металлов: алюминий Al, кадмий Cd, натрий Na, серебро Ag, калий K, никель Ni, свинец Pb, кобальт Co, бериллий Be, литий Li, сурьма Sb, висмут Bi, магний Mg, цинк Zn, вольфрам W, олово Sn, уран U, железо Fe, палладий Pd, цирконий Zr, марганец Mn, платина Pt, золото Au, медь Cu, родий Rh, таллий Tl, молибден Mo, тантал Ta, иридий Ir.
Следует отметить, что теплопроводность металлов изменяется в широких пределах и может отличаться в десятки раз в одних и тех же условиях. Например, из приведенных в таблице металлов, наибольшей теплопроводностью обладает такой металл, как серебро Ag — его коэффициент теплопроводности равен 392 Вт/(м·град) при 100°С и это самый теплопроводный металл. Наименьшее значение теплопроводности при этой же температуре соответствует металлу висмут Bi с теплопроводностью всего 7,7 Вт/(м·град).
Теплопроводность большинства металлов при нагревании снижается. Их максимальная теплопроводность достигается при низких отрицательных температурах. Например, при температуре минус 100°С серебро имеет теплопроводность 419,8, а висмут — 11,9 Вт/(м·град).
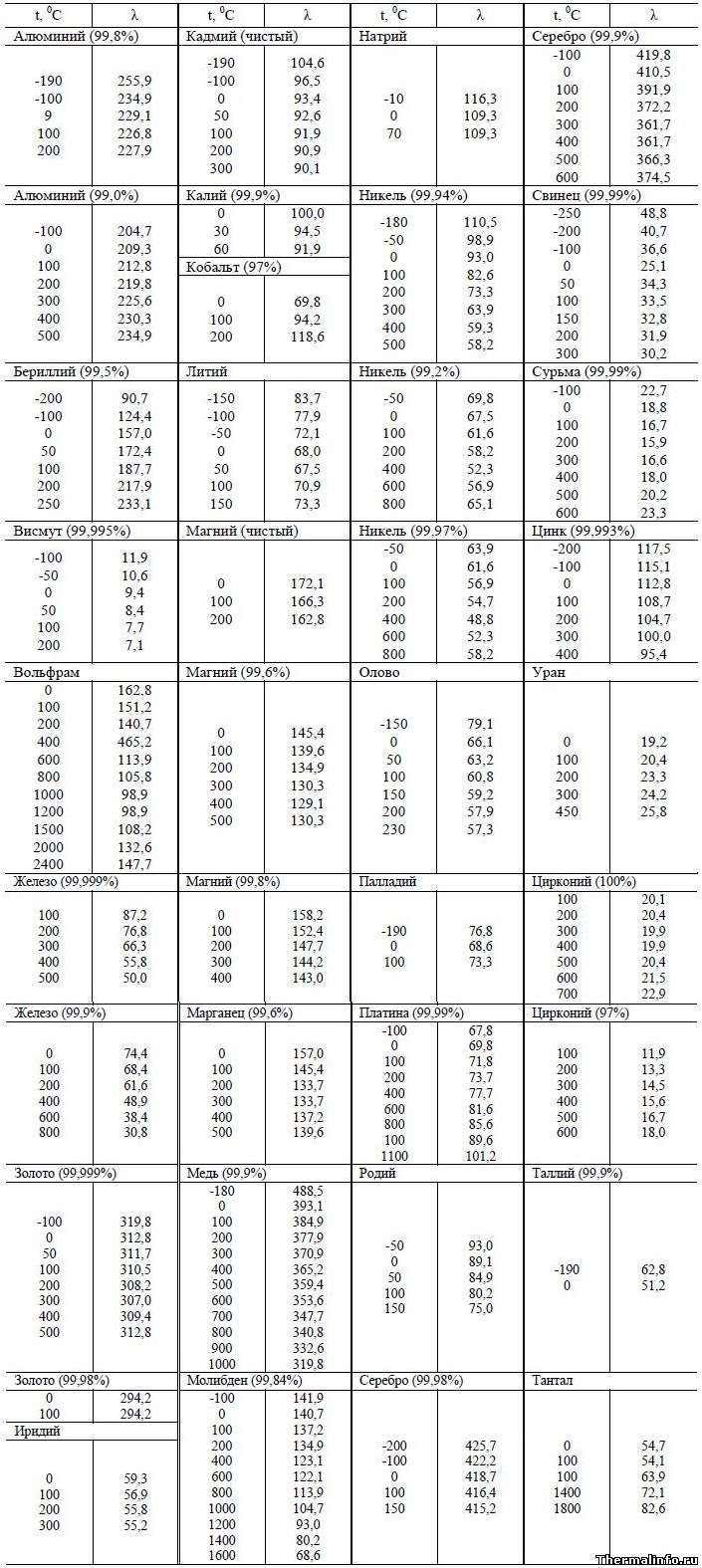
Примечание: В таблице также даны значения теплопроводности металлов сверх-высокой чистоты (до 99,999%). Значение коэффициента теплопроводности в таблице указано в размерности Вт/(м·град).
Добавить комментарий Отменить ответ
Теплопроводность строительных материалов, их плотность и теплоемкость
Плотность, теплопроводность и удельная теплоемкость строительных и других популярных материалов. Более 400 материалов в таблице!
Плотность воды, теплопроводность и физические свойства H2O
Подробные таблицы значений плотности воды, ее теплопроводности и других теплофизических свойств в зависимости от температуры…
Физические свойства воздуха: плотность, вязкость, удельная теплоемкость
Таблицы физических свойств воздуха: плотность воздуха, его удельная теплоемкость и вязкость в зависимости от температуры…
Теплопроводность стали и чугуна. Теплофизические свойства стали
Теплопроводность стали и чугуна, физические свойства стали в таблицах при различной температуре…
Физические свойства и допустимая температура применения сплавов магния
Физические свойства сплавов магния: плотность, коэффициент теплопроводности, удельная теплоемкость, КТЛР, максимальная температура применения и др.
Оргстекло: тепловые и механические характеристики
Рассмотрены тепловые, механические, оптические и электрические характеристики органического стекла…
Физические свойства технической соли
Насыпная плотность, удельная теплоемкость, коэффициент теплопроводности и другие физические свойства технической соли…
Характеристики теплоизоляционных плит Изорок (Isoroc)
Плотность, коэффициент теплопроводности и другие важнейшие характеристики теплоизоляционных плит Изорок различных модификаций…
Физические свойства сернистого газа: плотность, теплопроводность SO2
Рассмотрены физические свойства сернистого газа (SO2, диоксид серы) при нормальном атмосферном давлении в зависимости от…
Температура плавления припоя. Свойства припоев и подшипниковых материалов
Температура плавления и другие свойства припоев на основе олова и свинца В таблице представлена температура…

Теплопроводность, теплоемкость и плотность олова Sn
Теплопроводность, теплоемкость и плотность олова зависят от температуры и структуры этого металла. При атмосферном давлении…
Плотность мяса и его теплофизические свойства
Плотность мяса Плотность мяса зависит от его температуры, жирности и содержания влаги. С ростом температуры…
Свойства топлива и масел
Теплофизические свойства топлива и масел. Температура воспламенения В таблице представлены следующие свойства минеральных масел и…
Свойства аргона Ar, плотность аргона и его теплопроводность
Свойства аргона (газ) при различных температурах В таблице представлены теплофизические свойства аргона в газообразном состоянии…
Плотность жидкостей
Приведена таблица плотности жидкостей при различных температурах и атмосферном давлении для наиболее распространенных жидкостей. Значения…
Характеристики масла АМГ-10: плотность, вязкость, теплоемкость, теплопроводность
Характеристики масла АМГ-10 при температуре от 20 до 100°С: плотность, вязкость, теплоемкость, теплопроводность. Указаны также температуры кипения и замерзания…
Свойства маргарина
Свойства маргарина распространенных сортов Плотность, теплоемкость, теплопроводность и температуропроводность представлены для животного, безмолочного и сливочного…
Критериальные уравнения теплообмена: расчет теплоотдачи в трубах и каналах
Теплоотдача при вынужденном течении жидкости в трубах и каналах
Теплоотдача в трубах и каналах может происходить при вынужденном или свободном характере конвекционных потоков (возможны также их сочетания в случае существенного влияния гравитационных сил).
При вынужденном течении (вынужденная конвекция) жидкость нагнетается или отводится под действием сил внешнего давления, например, ветра, насоса или вентилятора.
Свободное течение жидкости происходит под действием подъемных (гравитационных) сил за счет изменения ее плотности из-за разницы температуры – слой жидкости с меньшей плотностью стремиться занять верхнее положение относительно холодного слоя (свободная или естественная конвекция).
Интенсивность теплоотдачи, как при вынужденной, так и при свободной конвекции характеризуется коэффициентом теплоотдачи α, имеющим размерность Вт/(м 2 ·град), который определяется по формуле:
Nu – число Нуссельта; λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);
d – эквивалентный диаметр, равный
F – площадь сечения канала, м 2 ; П – периметр канала, м.
Для трубы круглого сечения, эквивалентный диаметр равен внутреннему диаметру трубы.
В целом, расчет коэффициента теплоотдачи сводится к определению числа Нуссельта, значение которого задается соответствующими критериальными уравнениями конвективного теплообмена, зависящими от режима течения жидкости и формы канала.
Течение жидкости в трубах определяется значением числа Рейнольдса Re и в зависимости от его величины может быть ламинарным, переходным или турбулентным.
- Ламинарный режим течения жидкости характеризуется величиной числа Re до 2300.
- При значении числа Re от 2300 до 10000 режим течения в трубах является переходным.
- Турбулентный режим течения в трубах наблюдается при числах Re более 10000.
Число (критерий) Рейнольдса представляет собой безразмерный комплекс, связывающий скоростные и вязкостные характеристики жидкости с определяющим размером канала (для трубы – это ее диаметр).
Число Re определяется по формуле:
w – скорость течения жидкости, м/с; d – эквивалентный диаметр канала, м; ν — кинематическая вязкость жидкости при средней температуре, м 2 /с.
Теплоотдача в трубах и каналах существенно зависит от режима течения жидкости. При ламинарном режиме интенсивность теплоотдачи значительно меньше, чем при развитом турбулентном.
Теплоотдача при ламинарном течении в трубах и каналах
Ламинарный режим течения жидкости обычно характеризуется низкой скоростью потока. При этом в некоторых случаях влиянием конвекции, обусловленной действием гравитационных сил, пренебрегать нельзя.
Для выбора правильного критериального уравнения теплообмена и оценки влияния естественной конвекции на интенсивность теплопередачи при ламинарном режиме служит критерий Грасгофа Gr.
g – ускорение свободного падения, м/с 2 ;
β – температурный коэффициент объемного расширения, град -1 ;
d – эквивалентный диаметр канала, м;
ν — кинематическая вязкость жидкости при средней температуре, м 2 /с;
Δt – средняя разность температур жидкости и стенки, °С.
Теплоотдача при ламинарном течении в трубах и каналах с учетом естественной конвекции. Если величина комплекса GrPr превышает 8·10 5 , то расчет коэффициента теплоотдачи необходимо проводить с учетом влияния естественной конвекции в потоке жидкости по следующему критериальному уравнению:
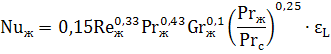
Индекс «ж» означает, что свойства среды, входящие в критерии подобия Re, Pr и Gr берутся при средней температуре жидкости.
Число Прандтля с индексом «с» Prс берется для жидкости при температуре стенки.
εL – коэффициент, учитывающий изменение теплоотдачи по длине трубы или канала. Его можно определить с помощью таблицы:
| L/d | 1 | 2 | 5 | 10 | 15 | 20 | 30 | 40 | 50 |
|---|---|---|---|---|---|---|---|---|---|
| εL | 1,9 | 1,7 | 1,44 | 1,28 | 1,18 | 1,13 | 1,05 | 1,02 | 1 |
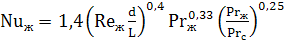
L – длина трубы (канала), м.
Представленные критериальные уравнения теплообмена при ламинарном режиме позволяют определить среднее значение числа Нуссельта, по величине которого можно рассчитать средний коэффициент теплоотдачи:
λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);
d – эквивалентный диаметр, м.
Теплоотдача в трубах и каналах при турбулентном режиме
Теплоотдача в трубах и каналах при турбулентном режиме осуществляется путем передачи тепла при интенсивном перемешивании слоев жидкости. Критериальное уравнение теплообмена для расчета средней теплоотдачи в трубах и каналах в этом случае имеет вид:
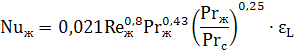
Критерии подобия Re и Pr берутся при средней температуре жидкости. Число Прандтля с индексом «с» Prс берется при температуре стенки.
Представленное критериальное уравнение применяется в диапазоне чисел Re от 1·10 4 до 5·10 6 и Pr от 0,6 до 2500.
εL – коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы или канала при турбулентном режиме течения. Значения εL приведены в следующей таблице при различных числах Рейнольдса и отношениях длины канала к его эквивалентному диаметру:
| Reж | L/d | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 5 | 10 | 15 | 20 | 30 | 40 | 50 | |
| 1·10 4 | 1,65 | 1,5 | 1,34 | 1,23 | 1,17 | 1,13 | 1,07 | 1,03 | 1 |
| 2·10 4 | 1,51 | 1,4 | 1,27 | 1,18 | 1,13 | 1,1 | 1,05 | 1,02 | 1 |
| 5·10 4 | 1,34 | 1,27 | 1,18 | 1,13 | 1,1 | 1,08 | 1,04 | 1,02 | 1 |
| 1·10 5 | 1,28 | 1,22 | 1,15 | 1,1 | 1,08 | 1,06 | 1,03 | 1,02 | 1 |
| 1·10 6 | 1,14 | 1,11 | 1,08 | 1,05 | 1,04 | 1,03 | 1,02 | 1,01 | 1 |
Расчет теплоотдачи в изогнутых трубах и каналах проводится по тому же критериальному уравнению с добавлением множителя — поправки на действие центробежных сил, которая определяется по формуле:
R — радиус изгиба трубы или канала, м; d – эквивалентный диаметр трубы или канала, м.
Теплоотдача в изогнутых трубах проходит более интенсивно, чем в прямых, за счет большего вихреобразования и лучшего перемешивания жидкости.
Расчет теплоотдачи при вынужденной конвекции
Пример расчета. Рассчитаем средний коэффициент теплоотдачи воды, текущей по трубопроводу длиной 1 м, диаметром d=0,01 м с расходом Q=20 л/мин. Средняя температура воды tж=50°С, температура стенки трубы tс=10°С.
1. Определим физические свойства воды при температуре 50°С:
- Теплопроводность воды λж= 0,648 Вт/(м·град);
- Плотность воды ρж=988 кг/м 3 ;
- Кинематическая вязкость воды νж=0,556·10 -6 , м 2 /с;
- Число Прандтля при температуре жидкости Prж=3,54;
- Число Прандтля при температуре стенки Prс=9,52.
2. Рассчитаем среднюю скорость течения воды w по трубе:
3. Определим число Рейнольдса Re:
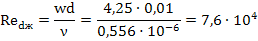
4. Поскольку число Рейнольдса имеет значение больше 1·10 4 , то режим течения является турбулентным и расчет теплоотдачи необходимо проводить по следующему критериальному уравнению:
Определим коэффициент εL по соотношению L/d=1/0,01=100. Поскольку L/d>50, то коэффициент εL=1.
Выполним расчет числа Нуссельта по приведенному критериальному уравнению:

5. Рассчитаем средний коэффициент теплоотдачи от воды к стенке трубы по формуле:
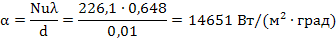
Таким образом, средний коэффициент теплоотдачи от воды к стенке трубы составляет 14,65 кВт/(м 2 ·град).
Теплоотдача при свободной конвекции в трубах и каналах
Теплообмен при свободном движении жидкости (или газа) происходит вследствие разности плотностей нагретых и холодных ее слоев. Интенсивность теплоотдачи жидкости в трубах и каналах при свободной конвекции существенно зависит от их положения в пространстве относительно силы тяжести.
Теплоотдача при свободной конвекции имеет различный характер в случаях свободного течения в неограниченном пространстве и теплообмена в ограниченном объеме (в узкой трубе или канале).
Свободная конвекция в неограниченном пространстве
Конвекция в неограниченном пространстве протекает, например при охлаждении трубопровода центрального отопления, расположенного на улице в безветренную погоду, вблизи от которого отсутствуют препятствия для движения воздушных потоков.
Горизонтальный канал или труба. Интенсивность теплоотдачи при свободной конвекции зависит от величины комплекса GrPr. При значении GrPr от 10 3 до 10 9 критериальное уравнение, описывающее среднюю теплоотдачу от поверхности горизонтальных труб и каналов, имеет вид:
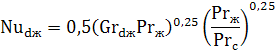
В качестве определяющего размера принимается наружный диаметр d канала или трубы.
Вертикальный канал (труба, пластина). Для вертикальных труб и каналов при значении GrPr от 10 3 до 10 9 критериальное уравнение, описывающее среднюю теплоотдачу, имеет вид:
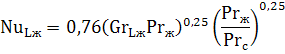
При GrPr>10 9 :
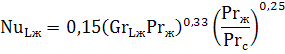
Примечание: В приведенных критериальных уравнениях теплообмена свойства жидкости, входящие в числа Gr и Pr, определяются при температуре окружающей среды. Число Прандтля с индексом «с» Prс берется для жидкости при температуре стенки. В качестве определяющего размера принимается длина L (высота) вертикально стоящей трубы или канала.
Свободная конвекция в ограниченном объеме
Теплообмен жидкости в ограниченном объеме при свободной конвекции характеризуется совместным протеканием процессов нагрева и охлаждения соседних слоев жидкости (или газа). Эти процессы сопровождаются сложным течением нисходящих и восходящих потоков, зависящих от рода жидкости, разницы температуры, формы канала и его геометрических размеров.
Для упрощения расчета таких сложных процессов конвективного теплообмена принято рассматривать их, как явление теплопроводности в щели толщиной δ с учетом понятия эквивалентного коэффициента теплопроводности λэк.
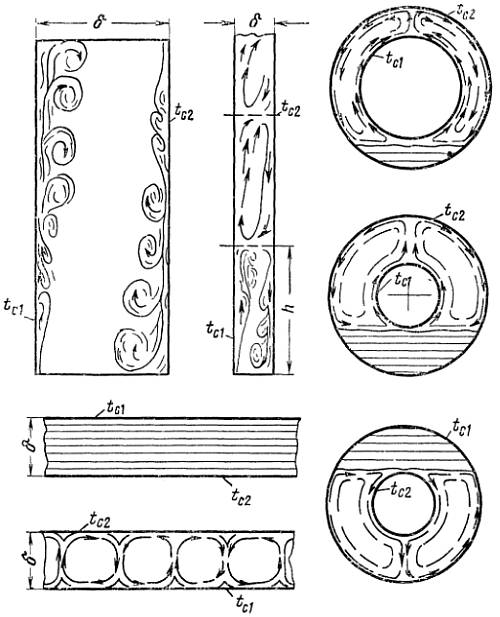
Эквивалентный коэффициент теплопроводности определяется по формуле:
Q — количество переданного тепла, Вт; δ — толщина слоя жидкости (или газа), м; F — площадь теплоотдающей поверхности, м 2 ; Δt=tc1-tc2 — температурный напор между нагретой и холодной стенками, °С.
Отношение эквивалентного коэффициента теплопроводности λэк к величине теплопроводности окружающей жидкости при средней температуре называется коэффициентом конвекции εк, который определяется значением комплекса GrPr.
При малых значениях комплекса GrPr коэффициент конвекции εк=1, то есть теплоотдача просходит только за счет теплопроводности среды (λэк=λ).
При 10 6 :
Примечание: Числа подобия Gr и Pr рассчитываются при средней температуре жидкости (или газа), равной tж=0,5(tc1+tc2). В качестве определяющего размера принимается δ — толщина слоя жидкости.
Расчет теплоотдачи при свободной конвекции
Пример расчета. Рассчитаем потери тепла естественной конвекцией от горизонтального трубопровода центрального отопления, находящегося на открытом воздухе. Диаметр трубопровода d=0,15 м, длина L=5 м, средняя температура наружной стенки tс=80°С. Температура окружающего воздуха tж=20°С.
1. Определим физические свойства воздуха при температуре 20°С:
- Теплопроводность воздуха λж= 0,0259 Вт/(м·град);
- Кинематическая вязкость воздуха νж=15,06·10 -6 , м 2 /с;
- Число Прандтля при температуре жидкости Prж=0,703;
- Число Прандтля при температуре стенки Prс=0,69;
- Коэффициент объемного расширения βж=1/(273+20)=0,00341 град -1 .
2. Вычислим число Грасгофа Gr по формуле:
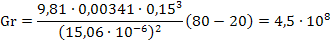
3. Определим значение комплекса GrPr:
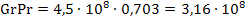
Этому значению комплекса соответствует следующее критериальное уравнение теплообмена при свободной конвекции в случае горизонтальной трубы:
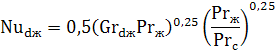
4. Вычислим значение числа Нуссельта Nu:
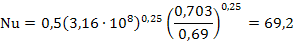
5. Рассчитаем коэффициент теплоотдачи от трубы α по формуле:
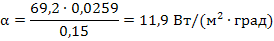
6. Определим потери тепла с боковой поверхности трубопровода по формуле:
Подставляя численные значения, окончательно получаем потерю тепла:
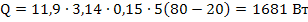
Таким образом, только путем естественной (свободной) конвекции рассмотренный трубопровод отопления отдает воздуху 1681 Вт тепла.
Теплопроводность цветных металлов, теплоемкость и плотность сплавов

Теплопроводность цветных металлов и технических сплавов
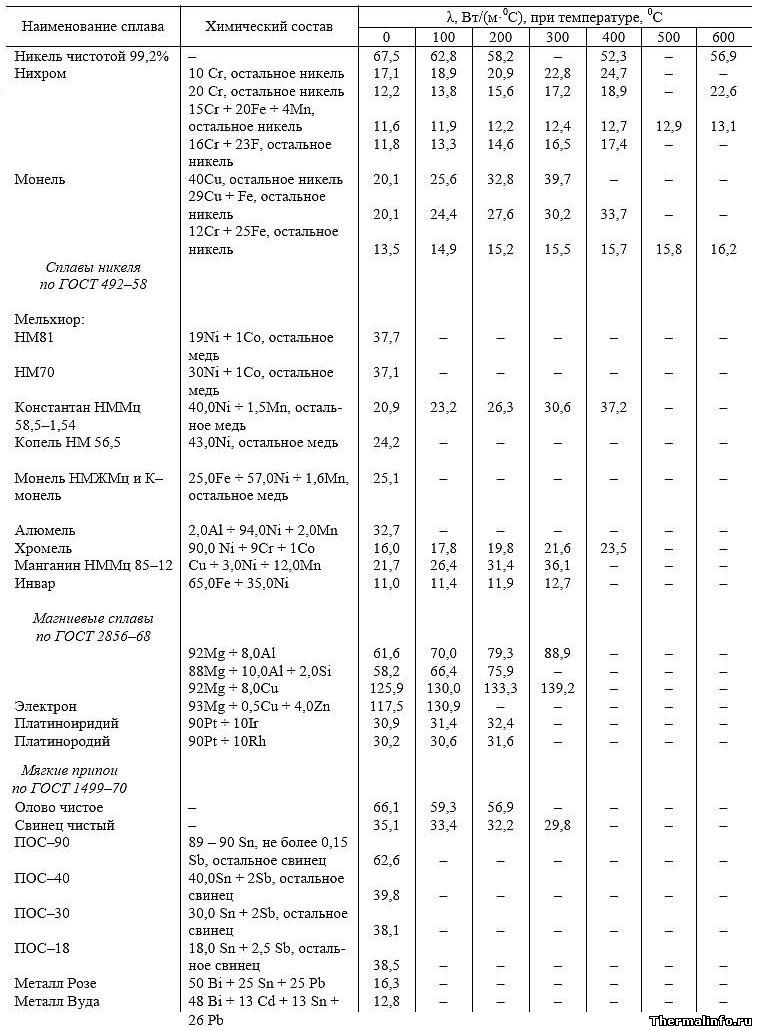
В таблице представлены значения теплопроводности металлов (цветных), а также химический состав металлов и технических сплавов в интервале температуры от 0 до 600°С.
Цветные металлы и сплавы: никель Ni, монель, нихром; сплавы никеля (по ГОСТ 492-58): мельхиор НМ81, НМ70, константан НММц 58,5-1,54, копель НМ 56,5, монель НМЖМц и К-монель, алюмель, хромель, манганин НММц 85-12, инвар; магниевые сплавы (по ГОСТ 2856-68), электрон, платинородий; мягкие припои (по ГОСТ 1499-70): олово чистое, свинец, ПОС-90, ПОС-40, ПОС-30, сплав Розе, сплав Вуда.
По данным таблицы видно, что высокую теплопроводность (при комнатной температуре) имеют магниевые сплавы и никель. Низкая же теплопроводность свойственна нихрому, инвару и сплаву Вуда.
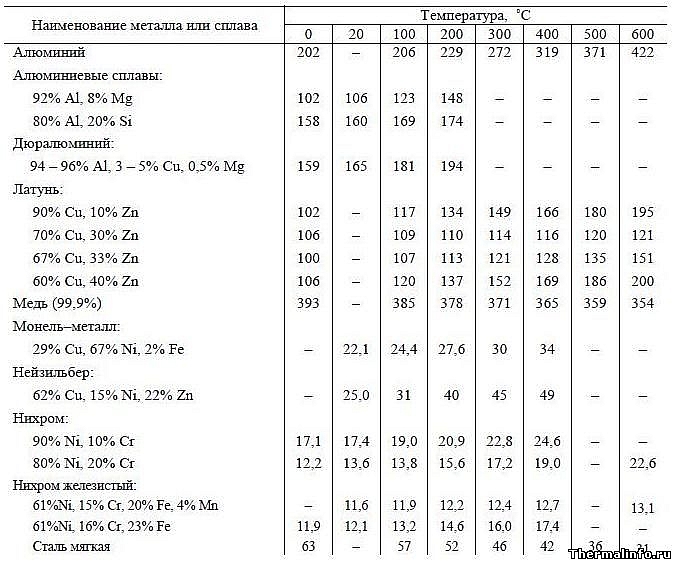
Коэффициенты теплопроводности алюминиевых, медных и никелевых сплавов
Теплопроводность металлов, алюминиевых, медных и никелевых сплавов в таблице дана в интервале температуры от 0 до 600°С в размерности Вт/(м·град).
Металлы и сплавы: алюминий, алюминиевые сплавы, дюралюминий, латунь, медь, монель, нейзильбер, нихром, нихром железистый, сталь мягкая. Алюминиевые сплавы имеют большую теплопроводность, чем латунь и сплавы никеля.
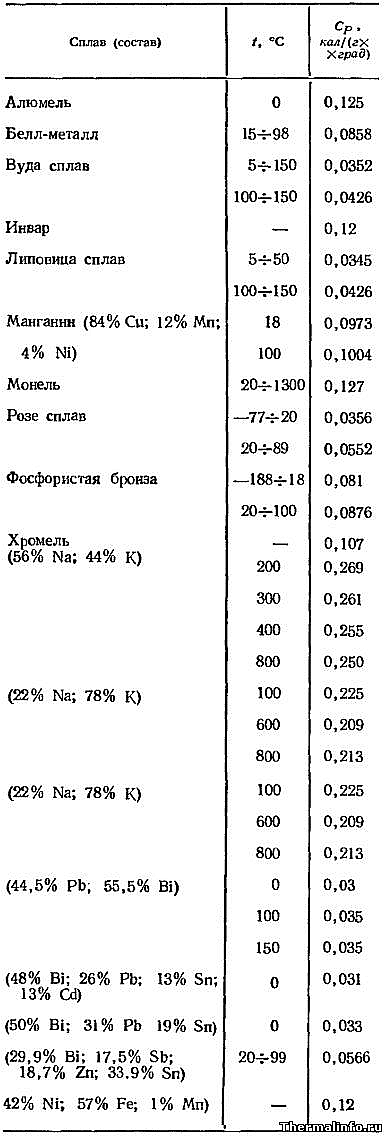
Коэффициенты теплопроводности сплавов
В таблице даны значения теплопроводности сплавов в интервале температуры от 20 до 200ºС.
Сплавы: алюминиевая бронза, бронза, бронза фосфористая, инвар, константан, манганин, магниевые сплавы, медные сплавы, сплав Розе, сплав Вуда, никелевые сплавы, никелевое серебро, платиноиридий, сплав электрон, платинородий.
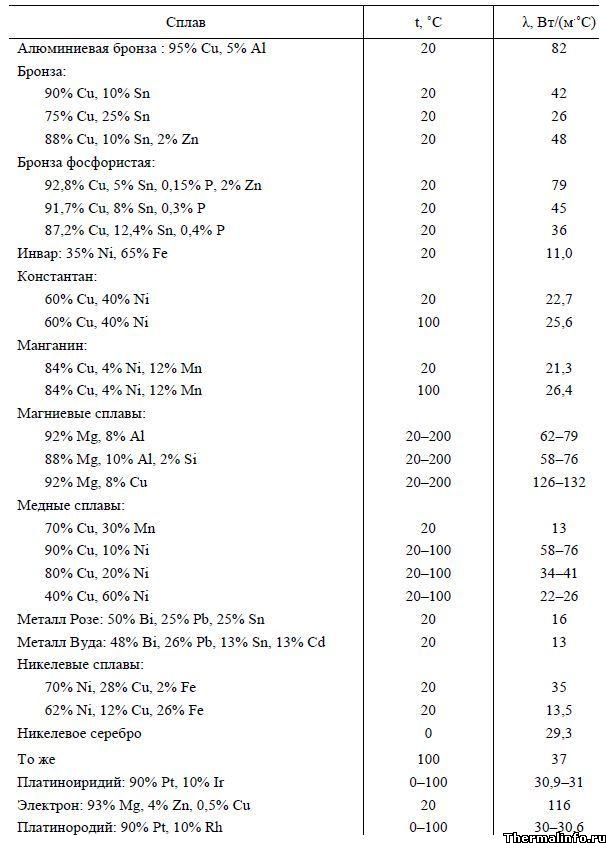
Удельное сопротивление и температурный коэффициент расширения (КТР) металлической проволоки (при 18ºС)
В таблице указаны значения удельного электрического сопротивления и КТР металлической проволоки, выполненной из различных металлов и сплавов.
Материал проволоки: алюминий, вольфрам, железо, золото, латунь, манганин, медь, никель, константан, нихром, олово, платина, свинец, серебро, цинк.
Как видно из таблицы, нихромовая проволока имеет высокое удельное электрическое сопротивление и успешно применяется в качестве спиралей накаливания нагревательных элементов множества бытовых и промышленных устройств.
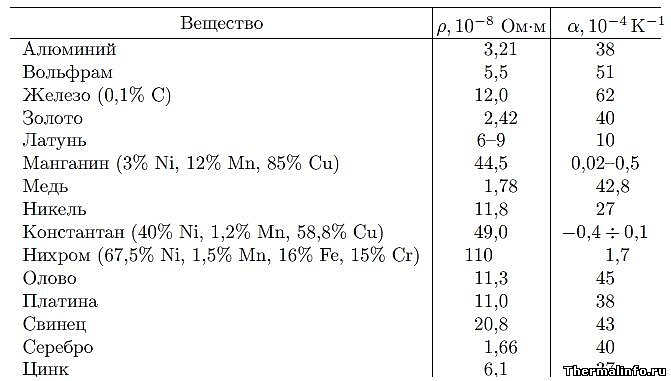
Удельная теплоемкость цветных сплавов
В таблице приведены величины удельной (массовой) теплоемкости двухкомпонентных и многокомпонентных цветных сплавов, не содержащих железа, при температуре от 123 до 1000К. Теплоемкость указана в размерности кДж/(кг·град).
Дана теплоемкость следующих сплавов: сплавы, содержащие алюминий, медь, магний, ванадий, цинк, висмут, золото, свинец, олово, кадмий, никель, иридий, платина, калий, натрий, марганец, титан, сплав висмут — свинец — олово, сплав висмут-свинец, висмут — свинец — кадмий, алюмель, сплав липовица, нихром, сплав розе.
Также существует отдельная таблица, где представлена удельная теплоемкость металлов при различных температурах.
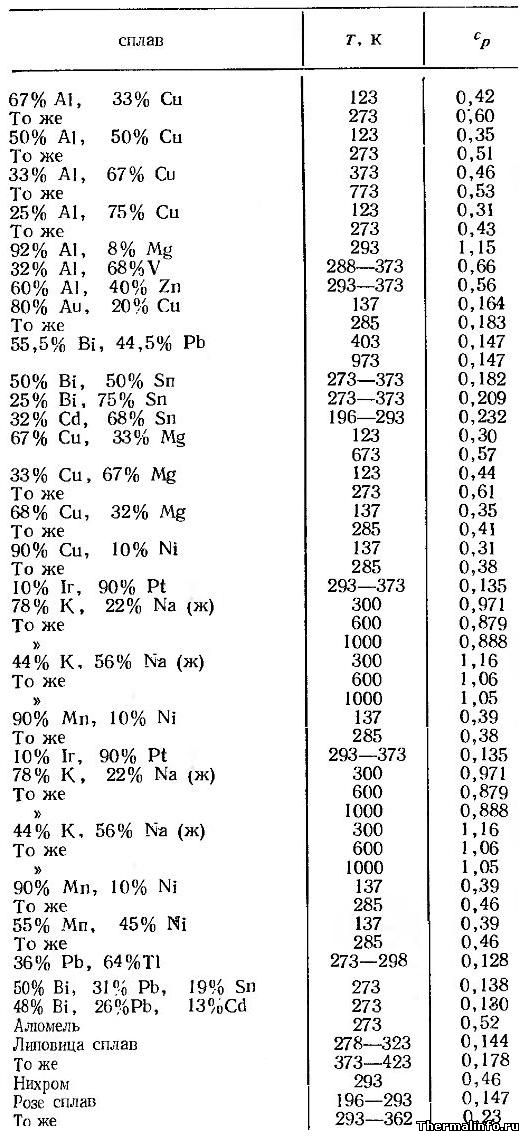
Удельная теплоемкость многокомпонентных специальных сплавов
Удельная (массовая) теплоемкость многокомпонентных специальных сплавов приведена в таблице при температуре от 0 до 1300ºС.
Размерность теплоемкости кал/(г·град).
Теплоемкость специальных сплавов: алюмель, белл-металл, сплав Вуда, инвар, липовица сплав, манганин, монель, сплав Розе, фосфористая бронза, хромель, сплав Na-K, сплав Pb — Bi, Pb — Bi — Sn, Zn — Sn — Ni — Fe — Mn.
Плотность сплавов
Представлена таблица значений плотности сплавов при комнатной температуре.
Приведены следующие сплавы: бронза, оловянистая, фосфористая, дюралюминий, инвар, константан, латунь, магналиум, манганин, монель — металл, платино — иридиевый сплав, сплав Вуда, сталь катаная, литая.

ПРИМЕЧАНИЕ: Будьте внимательны! Плотность сплавов в таблице указана в степени 10 -3 . Не забудьте умножить на 1000!
Например, плотность катанной стали изменяется в пределах от 7850 до 8000 кг/м 3 .
Таблицы теплопроводимости материалов (металлы, бетон, гранит, дерево и др.)
Взято из: «Примеры и задачи по курсу процессов и аппаратов химической технологии» /под ред. Романкова. Приложение.
Н.И. Кошкин, М.Г. Ширкевич. Справочник по элементарной физике // Издание девятое, М.: «Наука», 1982 г.
Коэффициент теплопроводности металлов
| Металл | Вт/(м•К) |
|---|---|
| Алюминий | 209,3 |
| Бронза | 47-58 |
| Железо | 74,4 |
| Золото | 312,8 |
| Латунь | 85,5 |
| Медь | 389,6 |
| Платина | 70 |
| Ртуть | 29,1 |
| Серебро | 418,7 |
| Сталь | 45,4 |
| Свинец | 35 |
| Серый чугун | 50 |
| Чугун | 62,8 |
Коэффициент теплопроводности других материалов
| Материал | Влажность массовая доля % | Вт/(м•К) |
|---|---|---|
| Бакелитовый лак | - | 0,29 |
| Бетон с каменным щебнем | 8 | 1,28 |
| Бумага обыкновенная | Воздушно-сухая | 0,14 |
| Винипласт | - | 0,13 |
| Гравий | Воздушно-сухая | 0,36 |
| Гранит | - | 3,14 |
| Глина | 15-20 | 0,7-0,93 |
| Дуб (вдоль волокон) | 6-8 | 0,35-0,43 |
| Дуб (поперек волокон) | 6-8 | 0,2-0,21 |
| Железобетон | 8 | 1,55 |
| Картон | Воздушно-сухая | 0,14-0,35 |
| Кирпичная кладка | Воздушно-сухая | 0,67-0,87 |
| Кожа | >> | 0,14-0,16 |
| Лед | - | 2,21 |
| Пробковые плиты | 0 | 0,042-0,054 |
| Снег свежевыпавший | - | 0,105 |
| Снег уплотненный | - | 0,35 |
| Снег начавший таять | - | 0,64 |
| Сосна (вдоль волокон) | 8 | 0,35-0,41 |
| Сосна (поперек волокон) | 8 | 0,14-0,16 |
| Стекло (обыкновенное) | - | 0,74 |
| Фторопласт-3 | - | 0,058 |
| Фторопласт-4 | - | 0,233 |
| Шлакобетон | 13 | 0,698 |
| Штукатурка | 6-8 | 0,791 |
Коэффициент теплопроводности асбеста и пенобетона при различных температурах
| Материал | -18 o С | 0 o С | 50 o С | 100 o С | 150 o С |
|---|---|---|---|---|---|
| Асбест | - | 0,15 | 0,18 | 0,195 | 0,20 |
| Пенобетон | 0,1 | 0,11 | 0,11 | 0,13 | 0,17 |
Коэффициент теплопроводности жидкости Вт/(м•К) при различных температурах
| Материал | 0 o С | 50 o С | 100 o С |
|---|---|---|---|
| Анилин | 0,19 | 0,177 | 0,167 |
| Ацетон | 0,17 | 0,16 | 0,15 |
| Бензол | - | 0,138 | 0,126 |
| Вода | 0,551 | 0,648 | 0,683 |
| Масло вазелиновое | 0,126 | 0,122 | 0,119 |
| Масло касторовое | 0,184 | 0,177 | 0,172 |
| Спирт метиловый | 0,214 | 0,207 | - |
| Спирт этиловый | 0,188 | 0,177 | - |
| Толуол | 0,142 | 0,129 | 0,119 |
Запись опубликована автором admin в рубрике Полезные материалы. Добавьте в закладки постоянную ссылку.
Читайте также:
