Какова работа выхода электронов из металла если
Как показывает опыт, свободные электроны при обычных температурах практически не, покидают металл. Следовательно, в поверхностном слое металла должно быть задерживающее электрическое поле, препятствующее выходу электронов из металла в окружающий вакуум. Работа, которую нужно затратить для удаления электрона из металла в вакуум, называется работой выхода. Укажем две вероятные причины появления работы выхода:
1. Если электрон по какой-то причине удаляется из металла, то в том месте, которое электрон покинул, возникает избыточный положительный заряд и электрон притягивается к индуцированному им самим положительному заряду.
2. Отдельные электроны, покидая металл, удаляются от него на расстояния порядка атомных и создают тем самым над поверхностью металла «электронное облако», плотность которого быстро убывает с расстоянием. Это облако вместе с наружным слоем положительных ионов решетки образует двойной электрический слой, поле которого подобно полю плоского конденсатора. Толщина этого слоя равна нескольким межатомным расстояниям (10 -10 — 10 -9 м). Он не создает электрического поля во внешнем пространстве, но препятствует выходу свободных электронов из металла.
Таким образом, электрон при вылете из металла должен преодолеть задерживающее его электрическое поле двойного слоя. Разность потенциалов в этом слое, называемая поверхностным скачком потенциала, определяется работой выхода (А) электрона из металла:
где е — заряд электрона. Так как вне двойного слоя электрическое поле отсутствует, то потенциал среды равен нулю, а внутри металла потенциал положителен и равен . Потенциальная энергия свободного электрона внутри металла равна — е и является относительно вакуума отрицательной. Исходи из этого можно
считать, что весь объем металла для электронов проводимости представляет потенциальную яму с плоским дном, глубина которой равна работе выхода А.
Работа выхода выражается в электрон-вольтах (эВ): 1 эВ равен работе, совершаемой силами поля при перемещении элементарного электрического заряда (заряда, равного заряду электрона) при прохождении им разности потенциалов в 1 В. Так как заряд электрона равен 1,6•l0 -19 Кл, то 1 эВ = 1,6•10 -1 9 Дж.
Работа выхода зависит от химической природы металлов и от чистоты их поверхности и колеблется в пределах нескольких электрон-вольт (например, у калия Л=2,2 эВ, у платины A = б,3 эВ). Подобрав определенным образом покрытие поверхности, можно значительно уменьшить paботу выхода. Например, если нанести на поверхность вольфрама (А =4,5 эВ) слой оксида щелочно-земельного металла (Са, Sr, Ba), то работа выхода снижается до 2 эВ.
§ 105. Эмиссионные явления и их применение
1. Термоэлектронная эмиссия — это испускание электронов нагретыми металлами. Концентрация свободных электронов в металлах достаточно высока, поэтому даже при средних температурах вследствие распределения электронов по скоростям (по энергии) некоторые электроны обладают энергией, достаточной для преодоления потенциального барьера на границе металла. С повышением температуры число электронов, кинетическая энергия теплового движения которых больше работы выхода, растет и явление термоэлектронной эмиссии становится заметным.

Исследование закономерностей термоэлектронной эмиссии можно провести с помощью простейшей двухэлектродной лампы — вакуумного диода, представляющего собой откачанный баллон, содержащий два электрода: катод К и анод А. В простейшем случае катодом служит нить из тугоплавкого металла (например, вольфрама), накаливаемая электрическим током. Анод чаще всего имеет форму металлического цилиндра, окружающего катод. Если диод включить в цепь, как это показано на рис. 152, то при накаливании катода и подаче на анод положительного напряжения (относительно катода) в анодной цепи диода возникает ток. Если поменять полярность батареи Ба, то ток прекращается, как бы сильно катод ни накаливали. Следовательно, катод испускает отрицательные частицы — электроны.
Если поддерживать температуру накаленного катода постоянной и снять зависимость анодного тока Iа от анодного напряжения Ua — вольт-амперную характеристику (рис. 153), то оказывается, что она не является линейной, т. е. для вакуумного диода закон Ома не выполняется. Зависимость термоэлектронного тока I от анодного напряжения в области малых

положительных значений U описывается законом трех вторых (установлен русским физиком С. А. Богуславским (1883— 1923) и американским физиком И. Ленгмюром (1881 — 1957)):
I=BU 3/2 ,
где В — коэффициент, зависящий от формы и размеров электродов, а также их взаимного расположения.
При увеличении анодного напряжения ток возрастает до некоторого максимального значения Iнас, называемого током насыщения. Это означает, что почти все электроны, покидающие катод, достигают анода, поэтому дальнейшее увеличение напряженности поля не может привести к увеличению термоэлектронного тока. Следовательно, плотность тока насыщения характеризует эмиссионную способность материала катода.
Плотность тока насыщения определяется формулой Ричардсона — Дешмана, выведенной теоретически на основе квантовой статистики:
где А — работа выхода электронов из катода, Т — термодинамическая температура, С — постоянная, теоретически одинаковая для всех металлов (это не подтверждается экспериментом, что, по-видимому, объясняется поверхностными эффектами). Уменьшение работы выхода приводит к резкому увеличению плотности тока насыщения. Поэтому применяются оксидные катоды (например, никель, покрытый оксидом щелочно-земельного металла), работа выхода которых равна 1 —1,5 эВ.
На рис. 153 представлены вольт-амперные характеристики для двух температур катода: T1 и Т2, причем T2>T1. С повышением температуры катода испускание электронов с катода интенсивнее, при этом увеличивается и ток насыщения. При Ua=0 наблюдается анодный ток, т. е. некоторые электроны, эмиттируемые катодом, обладают энергией, достаточной для преодоления работы выхода и достижения анода без приложения электрического поля.
Явление термоэлектронной эмиссии используется в приборах, в которых необходимо получить поток электронов в вакууме, например в электронных лампах, рентгеновских трубках, электронных микроскопах и т. д. Электронные лампы широко применяются в электро- и радиотехнике, автоматике и телемеханике для выпрямления переменных токов, усиления электрических сигналов и переменных токов, генерирования электромагнитных колебаний и т. д. В зависимости от назначения в лампах используются дополнительные управляющие электроды.
2. Фотоэлектронная эмиссия — это эмиссия электронов из металла под действием света, а также коротковолнового электромагнитного излучения (например, рентгеновского). Основные закономерности этого явления будут разобраны при рассмотрении фотоэлектрического эффекта.
3. Вторичная электронная эмиссия — это испускание электронов поверхностью металлов, полупроводников или диэлектриков при бомбардировке их пучком электронов. Вторичный электронный поток состоит из электронов, отраженных поверхностью (упруго и неупруго отраженные электроны), и «истинно» вторичных электронов — электронов, выбитых из металла, полупроводника или диэлектрика первичными электронами.
Отношение числа вторичных электронов n2 к числу первичных п1, вызвавших эмиссию, называется коэффициентом вторичной электронной эмиссии:
Коэффициент б зависит от природы материала поверхности, энергии бомбардирующих частиц и их угла падения на поверхность. У полупроводников и диэлектриков б больше, чем у металлов. Это объясняется тем, что в металлах, где концентрация электронов проводимости велика, вторичные электроны, часто сталкиваясь с ними, теряют свою энергию и не могут выйти из металла. В полупроводниках и диэлектриках же из-за малой концентрации электронов проводимости столкновения вторичных электронов с ними происходят гораздо реже и вероятность выхода вторичных электронов из эмиттера возрастает в несколько раз.
Для примера на рис. 154 приведена качественная зависимость коэффициента вторичной электронной эмиссии б от энергии Е падающих электронов для KCl. С увеличением энергии электронов б возрастает, так как первичные электроны все глубже проникают в кристаллическую решетку и, следовательно, выбивают больше вторичных электронов. Однако при некоторой энергии первичных электронов 6 начинает уменьшаться. Это связано с тем, что с увеличением глубины проникновения первичных электронов вторичным все труднее вырваться на поверхность. Значение max для KCl достигает 12 (для чистых металлов оно не превышает 2).
Явление вторичной электронной эмиссии используется в фотоэлектронных умножителях (ФЭУ), применяемых для усиления слабых электрических токов. ФЭУ представляет собой вакуумную трубку с фотокатодом К и анодом А, между которыми расположено несколько электродов— эмиттеров (рис.155). Электроны, вырванные с фотокатода под действием света, попадают на эмиттер Э1, пройдя ускоряющую разность потенциалов между К и Э1. Из эмиттера Э1 выбивается электронов. Усиленный таким образом
электронный поток направляется на эмиттер Э2, и процесс умножения повторяется на всех последующих эмиттерах. Если ФЭУ содержит n эмиттеров, то на аноде А, называемом коллектором, получается усиленный в б" раз фотоэлектронный ток.
4. Автоэлектронная эмиссия — это эмиссия электронов с поверхности металлов под действием сильного внешнего электрического поля. Эти явления можно наблюдать в откачанной трубке, конфигурация электродов которой (катод — острие, анод — внутренняя поверхность трубки) позволяет при напряжениях примерно 10 3 В получать электрические поля напряженностью примерно 10 7 В/м. При постепенном повышении напряжения уже при напряженности поля у поверхности катода примерно 10 5 —10 6 В/м возникает слабый ток, обусловленный электронами, испускаемыми катодом. Сила этого тока увеличивается с повышением напряжения на трубке. Токи возникают при холодном катоде, поэтому описанное явление называется также холодной эмиссией. Объяснение механизма этого явления возможно лишь на основе квантовой теории.
Примеры решенных задач по физике на тему "Фотоэффект"
Ниже размещены условия задач и отсканированные решения. Если вам нужно решить задачу на эту тему, вы можете найти здесь похожее условие и решить свою по аналогии. Загрузка страницы может занять некоторое время в связи с большим количеством рисунков. Если Вам понадобится решение задач или онлайн помощь по физике- обращайтесь, будем рады помочь.
Явление фотоэффекта заключается в испускании веществом электронов под действием падающего света. Теория фотоэффекта разработана Эйнштейном и заключается в том, что поток света представляет собой поток отдельных квантов(фотонов) с энергией каждого фотона h n . При попадании фотонов на поверхность вещества часть из них передает свою энергию электронов. Если этой энергия больше работы выхода из вещества, электрон покидает металл. Уравнение эйнштейна для фотоэффекта: где — максимальная кинетическая энергия фотоэлектрона.
Длина волны красной границы фотоэффекта для некоторого металла составляет 307 нм. Максимальная кинетическая энергия фотоэлектронов – 1 эВ. Найти отношение работы выхода электрона к энергии падающего фотона.

Частота света красной границы фотоэффекта для некоторого металла составляет 6*10 14 Гц, задерживающая разность потенциалов для фотоэлектронов – 2В. Определить частоту падающего света и работу выхода электронов.

Работа выхода электрона из металла составляет 4,28эВ. Найти граничную длину волны фотоэффекта.

На медный шарик радает монохроматический свет с длиной волны 0,165 мкм. До какого потенциала зарядится шарик, если работа выхода электрона для меди 4,5 эВ?

Работа выхода электрона из калия составляет 2,2эВ, для серебра 4,7эВ. Найти граничные длину волны фотоэффекта.


Длина волны радающего света 0,165 мкм, задерживающая разность потенциалов для фотоэлектронов 3В. Какова работа выхода электронов?
Красная граница фотоэффекта для цинка 310 нм. Определить максимальную кинетическую энергию фотоэлектронов, если на цинк падает свет с длиной волны 200нм.

На металл с работой выхода 2,4эВ падает свет с длиной волны 200нм. Определить задерживающую разность потенциалов.

На металл падает свет с длиной волны 0,25 мкм, задерживающая разность потенциалов при этом 0,96В. Определить работу выхода электронов из металла.

При изменении длины волны падающего света максимальные скорости фотоэлектронов изменились в 3/4 раза. Первоначальная длина волны 600нм, красная граница фотоэффекта 700нм. Определить длину волны после изменения.


Работы выхода электронов для двух металлов отличаются в 2 раза, задерживающие разности потенциалов - на 3В. Определить работы выхода.

Максимальная скорость фотоэлектронов равно 2,8*10 8 м/с. Определить энергию фотона.
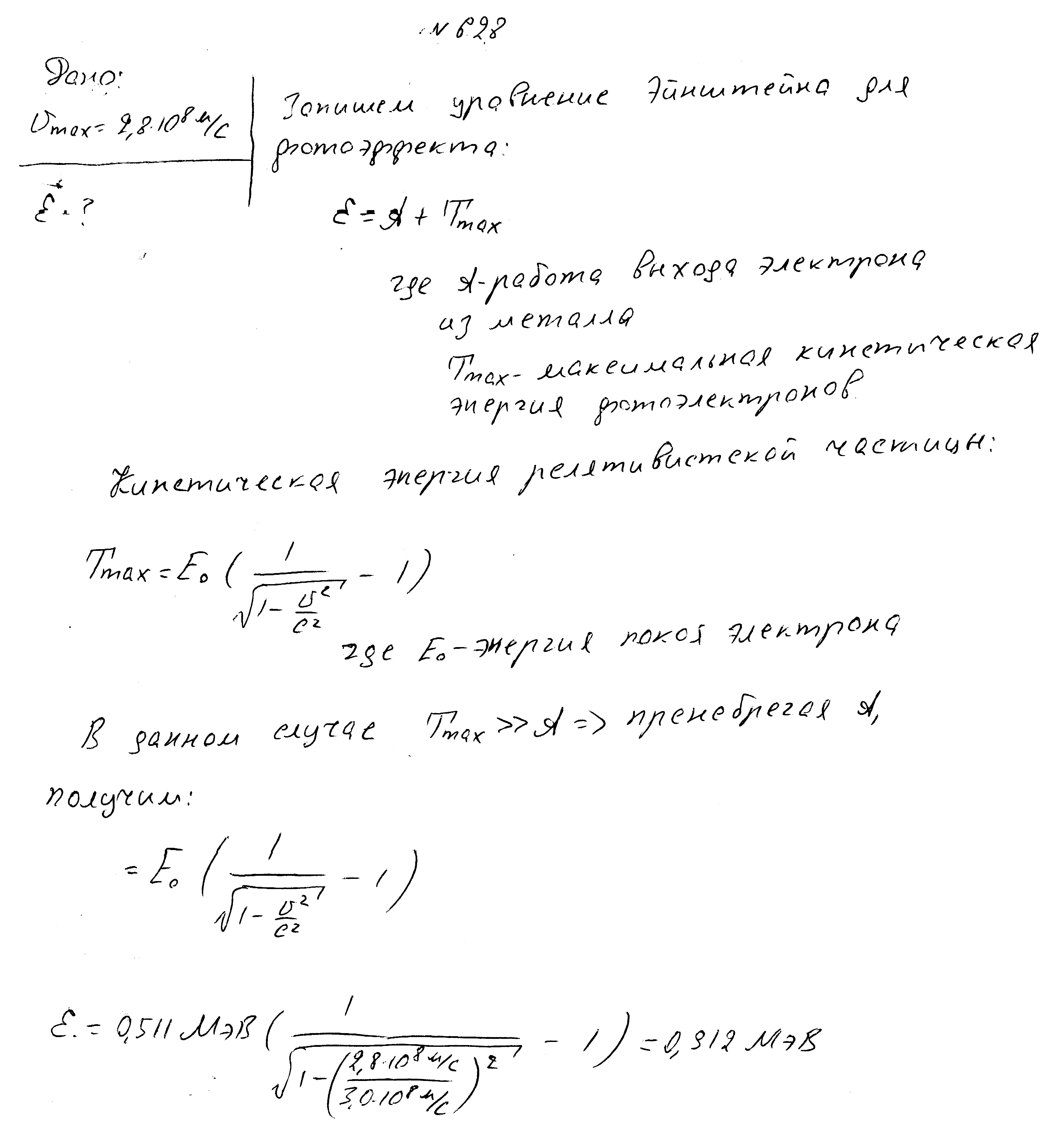
Энергии падающих на металл фотонов равны 1,27 МэВ. Найти максимальную скорость фотоэлектронов.

Максимальная скорость фотоэлектронов равно 0,98с, где с - скорость света в вакууме. Найти длину волны падающего света.
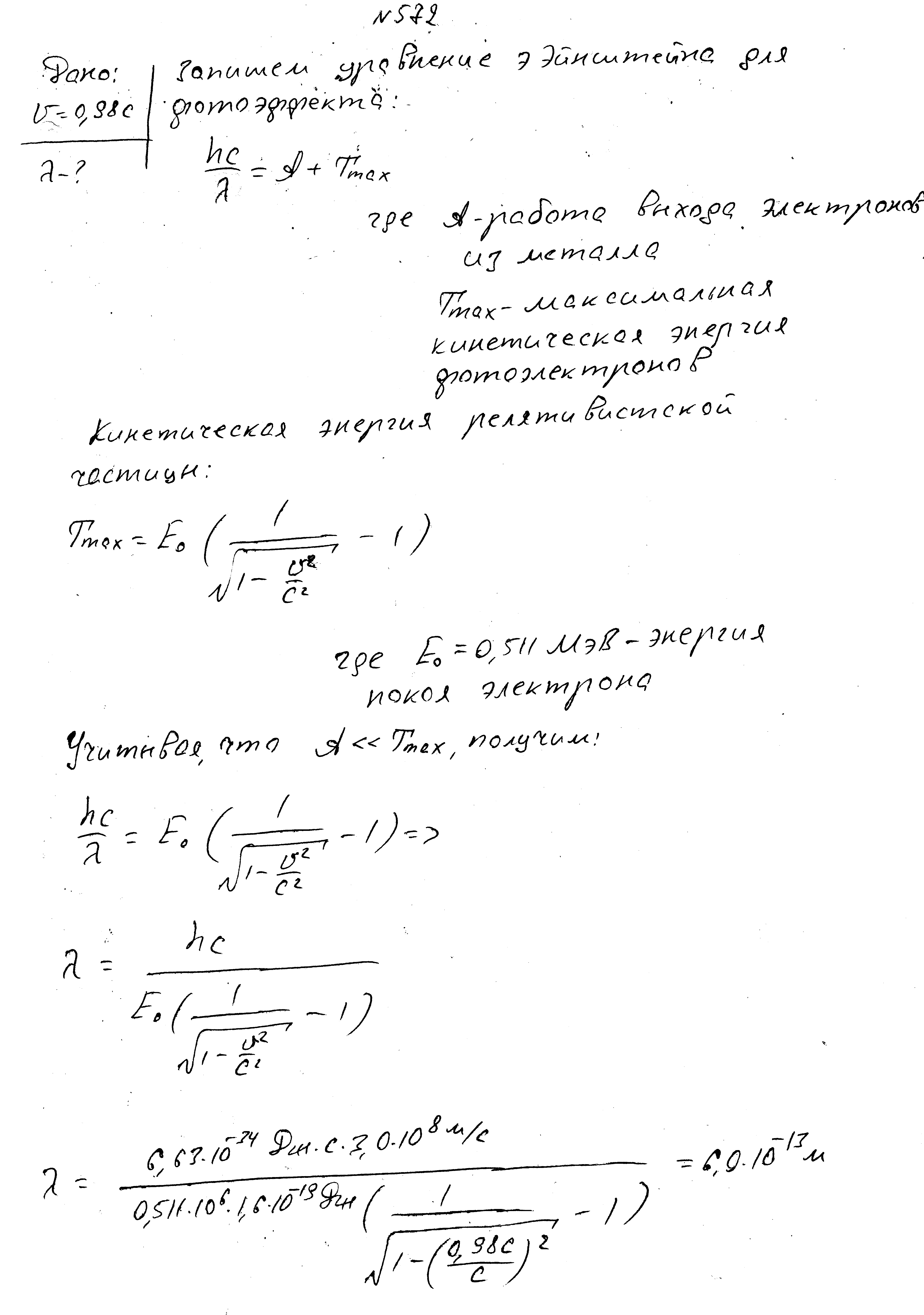
Энергия фотона в пучке света, падающего на поверхность металла, равно 1,53 МэВ. Определить максимальную скорость фотоэлектронов.
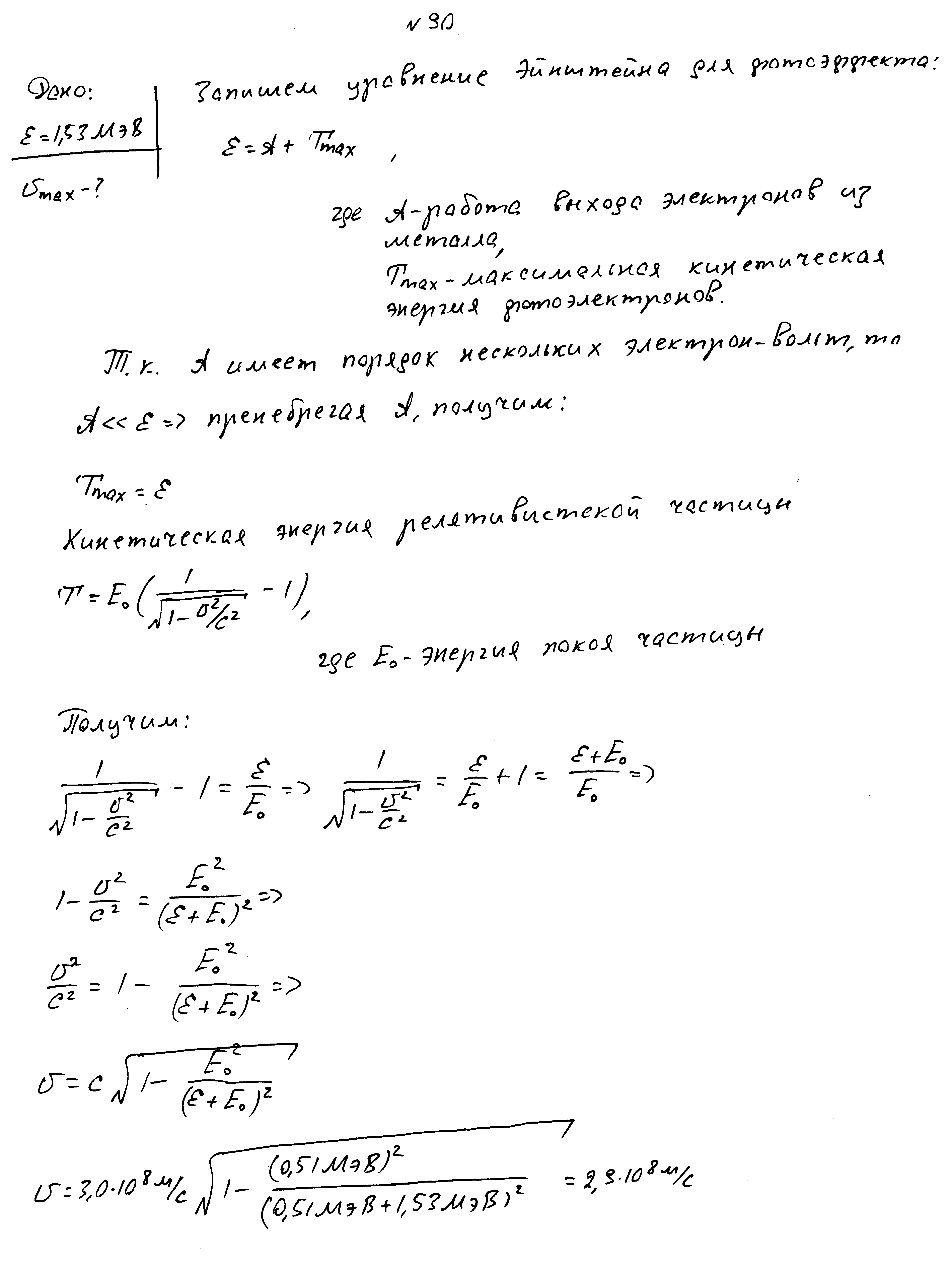
На шарик из металла падает свет с длиной волны 0,4 мкм, при этом шапик заряжается до потенциала 2В. До какого потенциала зарядится шарик, если длина волны станет равной 0,3 мкм?

После изменения длины волны падающего света в 1,5 раза задерживающая разность потенциалов изменилась с 1,6В до 3В. Какова работа выхода?
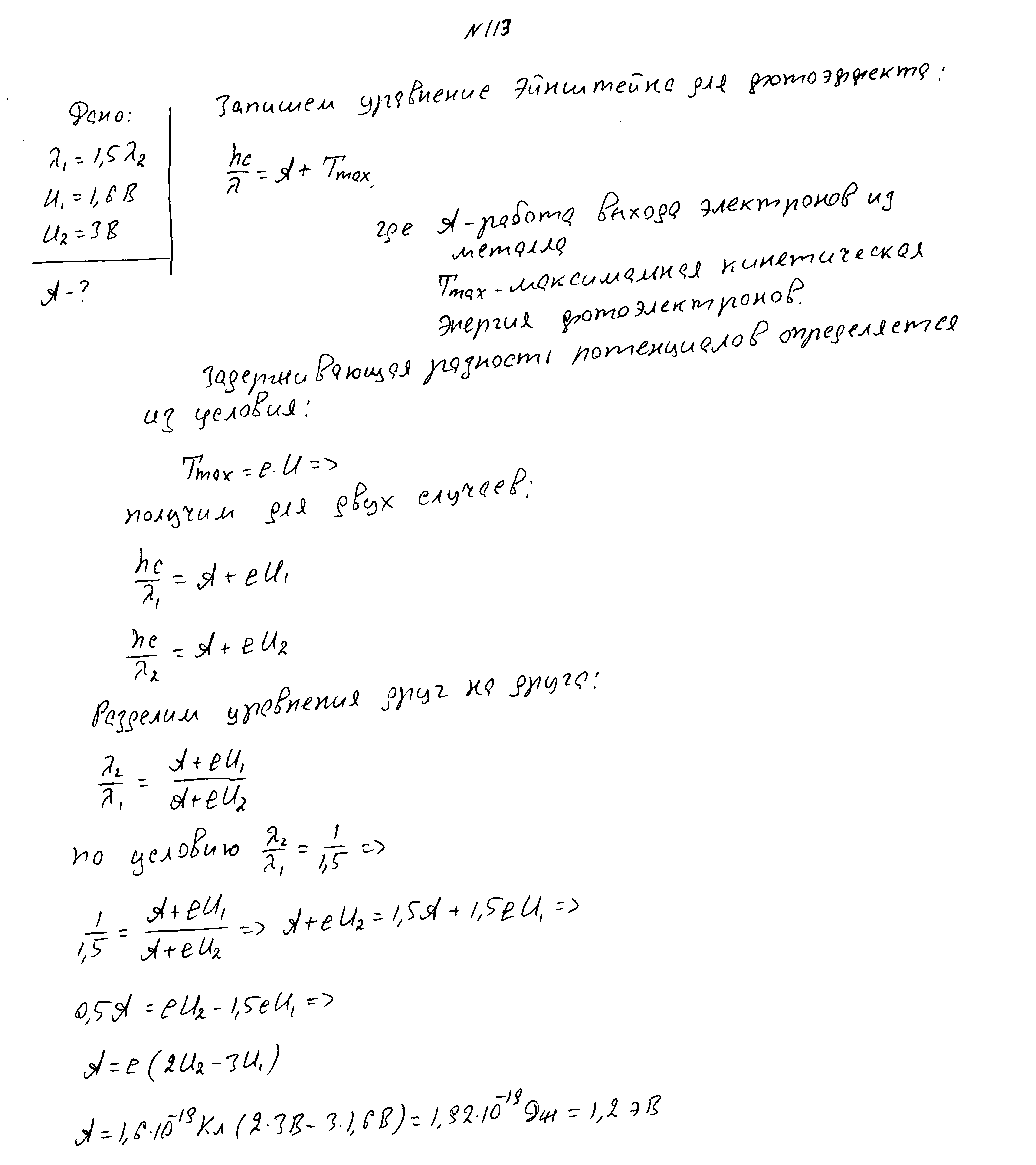
Красная граница фотоэффекта 560нм, частота падающего света 7,3*10 14 Гц. Найти максимальную скорость фотоэлектронов.
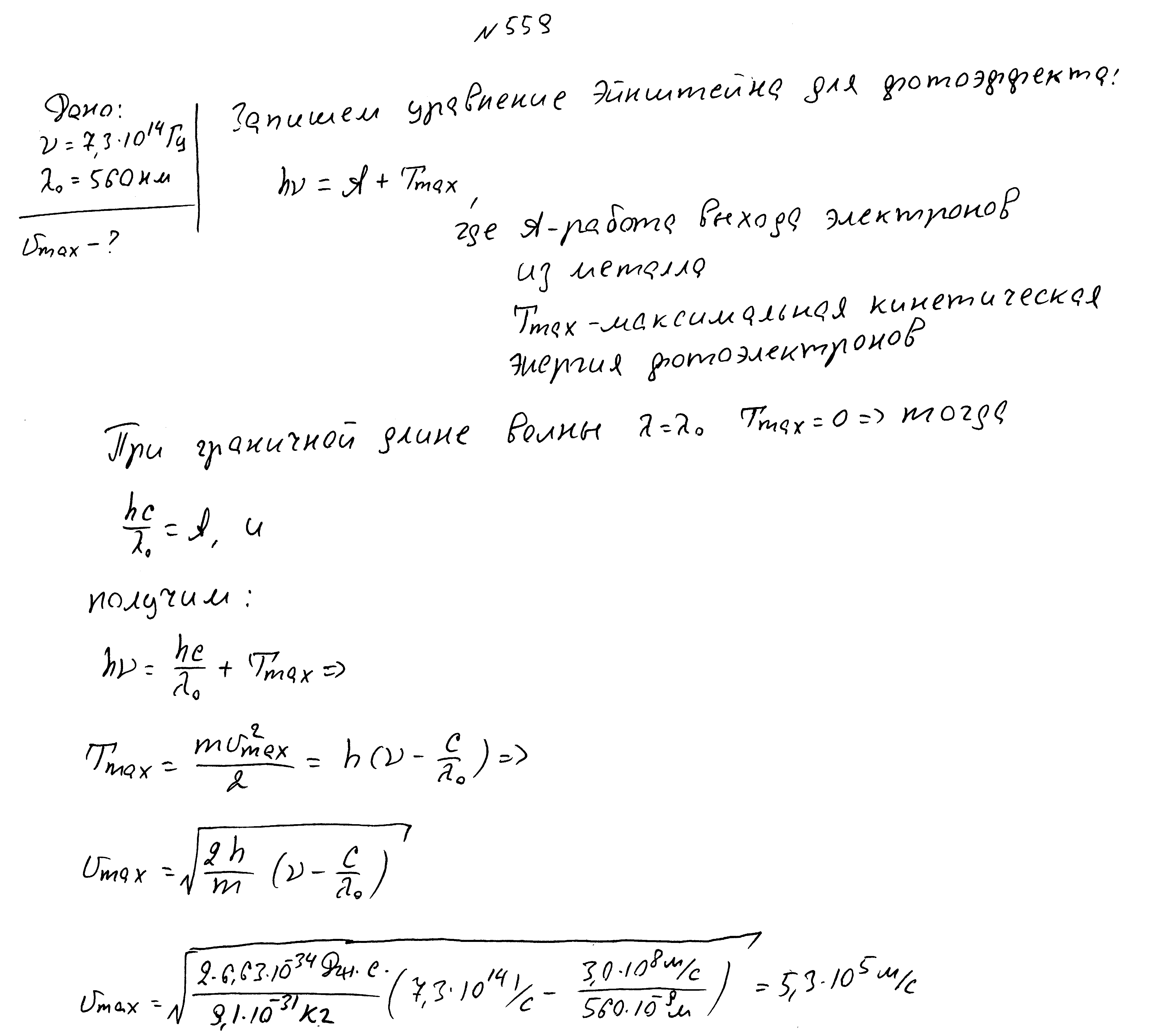
Красная граница фотоэффекта 2800 ангстрем, длина волны падающего света 1600 ангстрем. Найти работу выхода и максимальную кинетическую энергию фотоэлектрона.

Задерживащая разность потенциалов 1,5В, работа выхода электронов 6,4*10 -19 Дж. Найти длину волны падающего света и красную границу фотоэффекта.

Работа выхода электронов из металла равна 3,3 эВ. Во сколько раз изменилась кинетическая энергия фотоэлектронов. если длина волны падающего света изменилась с 2,5*10 -7 м до 1,25*10 -7 м?
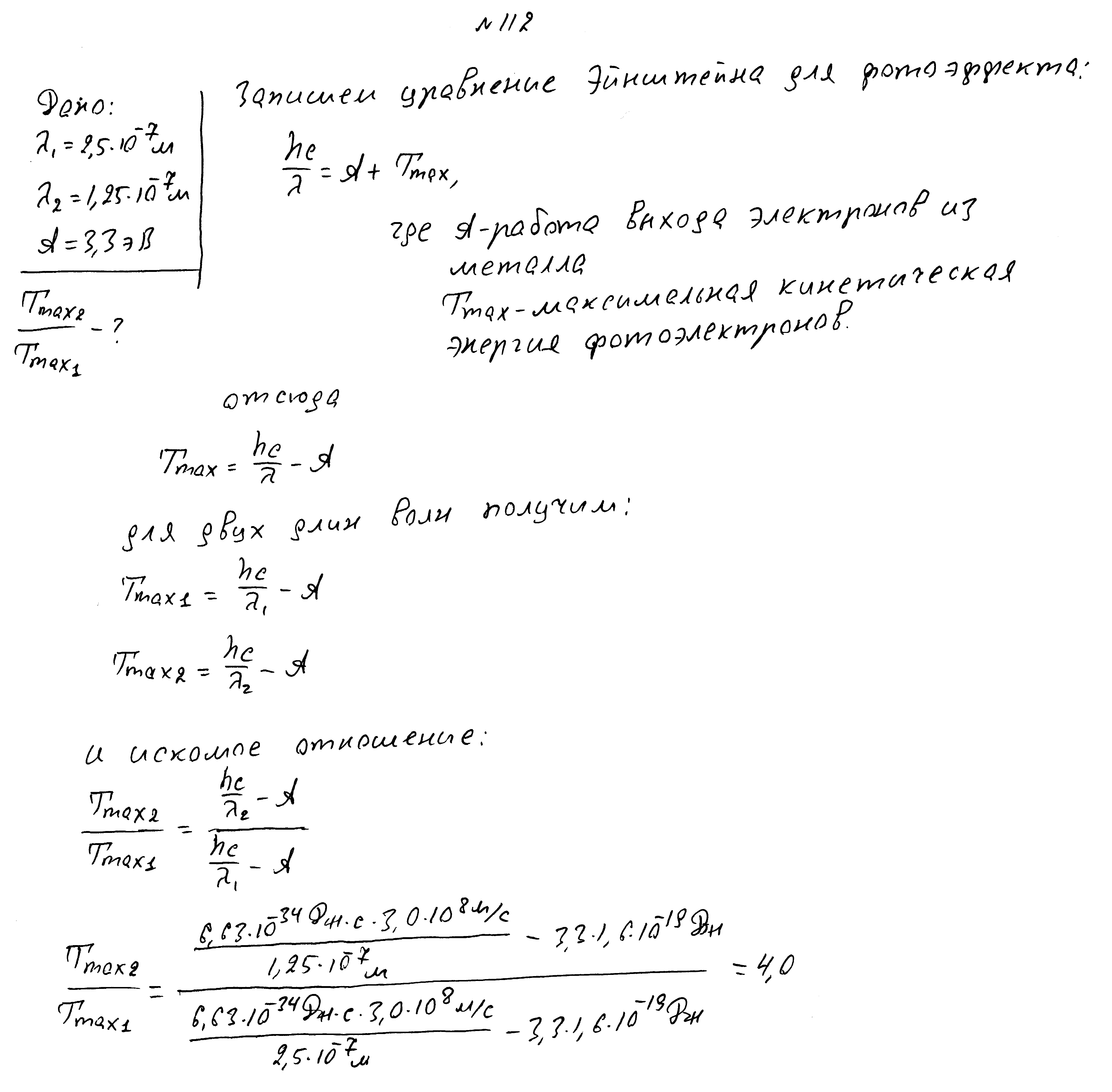
Найти максимальную скорость фотоэлектронов для видимого света с энергией фотона 8 эВ и гамма излучения с энергией 0,51 МэВ. Работа выхода электронов из металла 4,7 эВ.
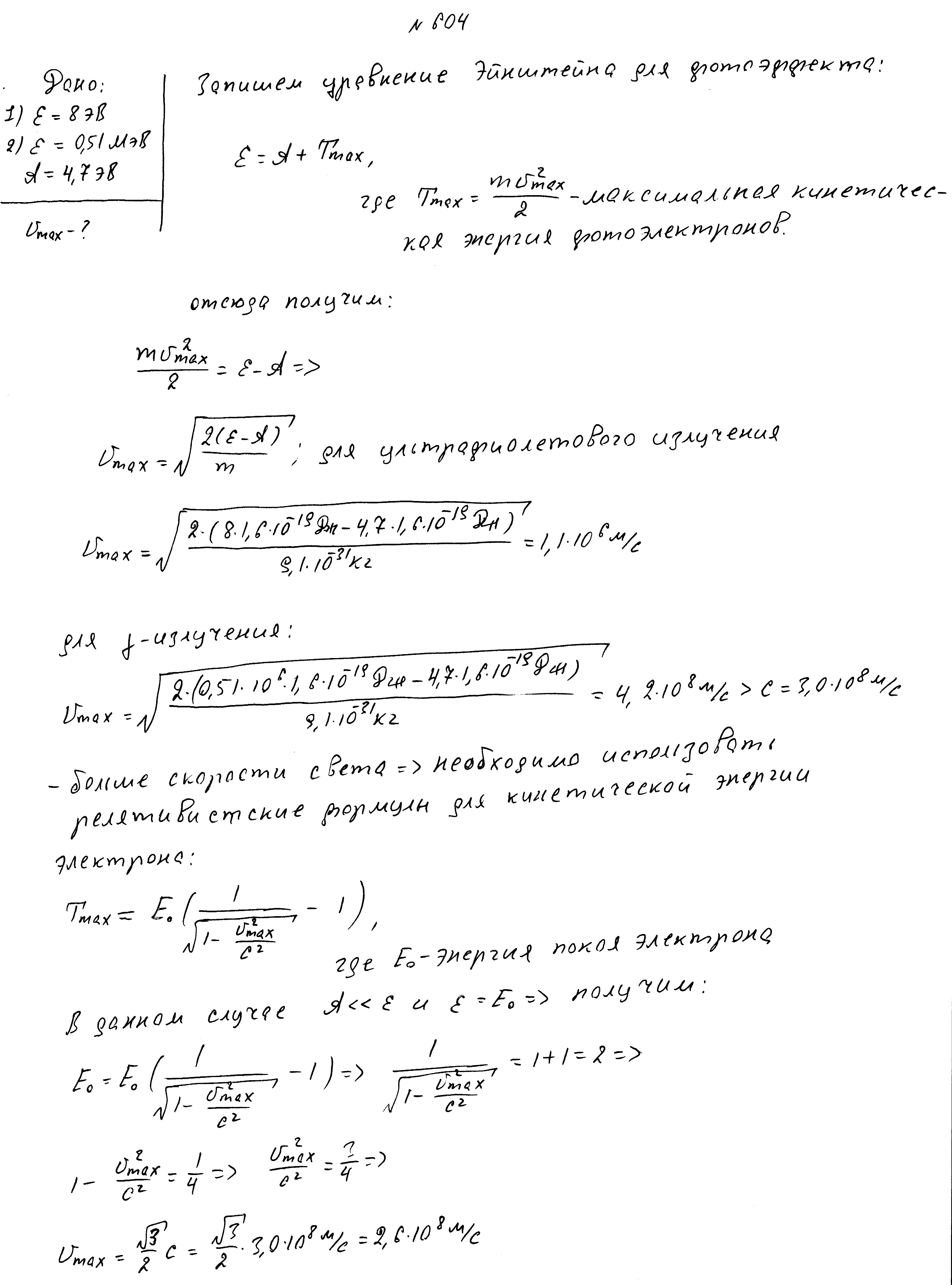
Фототок прекращается при задерживающей разности потенциалов 3,7 В. Работа выхода электронов равна 6,3 эВ. Какая работа выхода электронов у другого металла, если там фототок прекращается при разности потенциалов, большей на 2,3В.
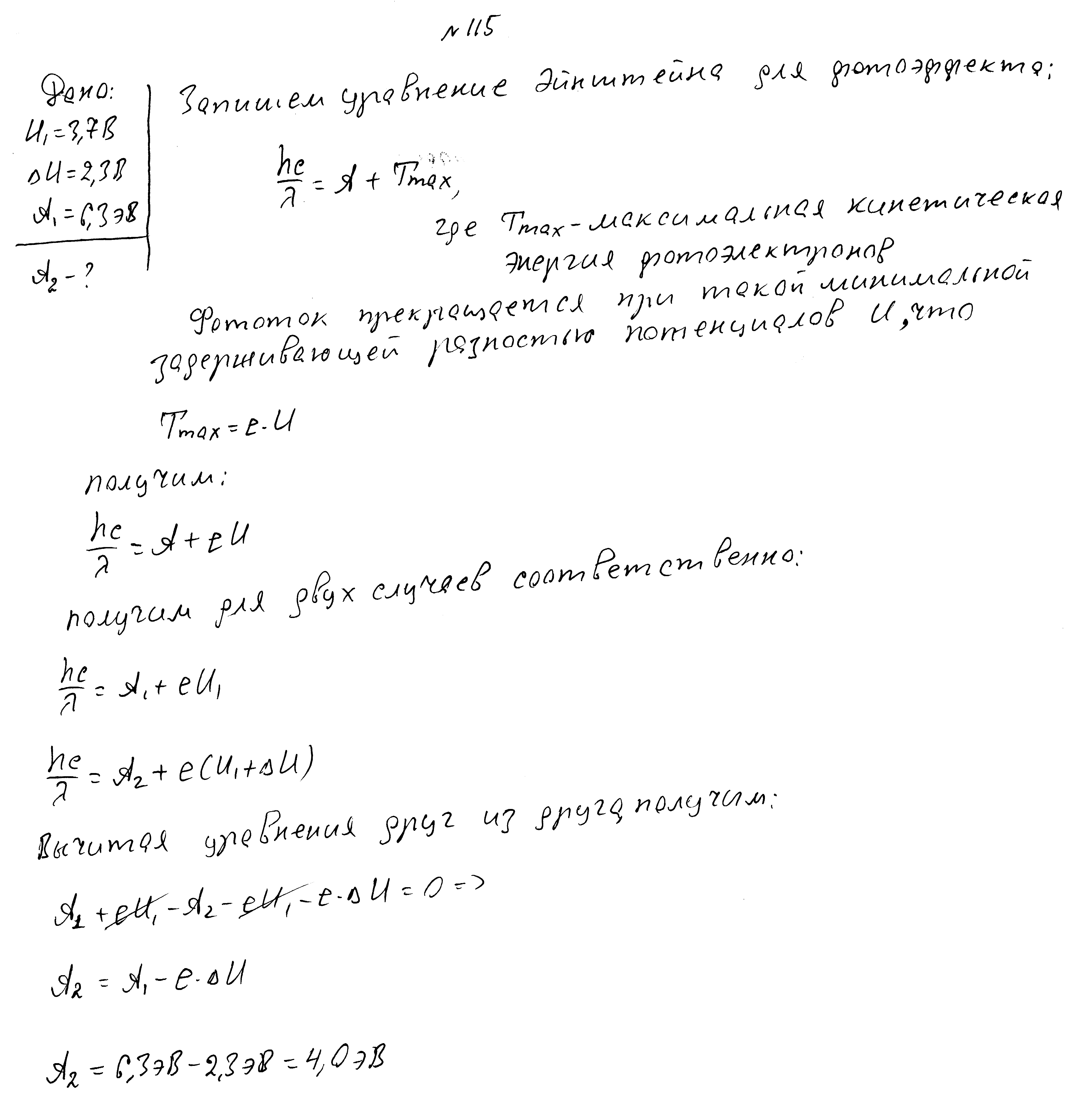
Работа выхода электронов из металла 4,5 эВ, энергия падающих фотонов 4,9 эВ. Чему равен максимальный импульс фотоэлектронов?
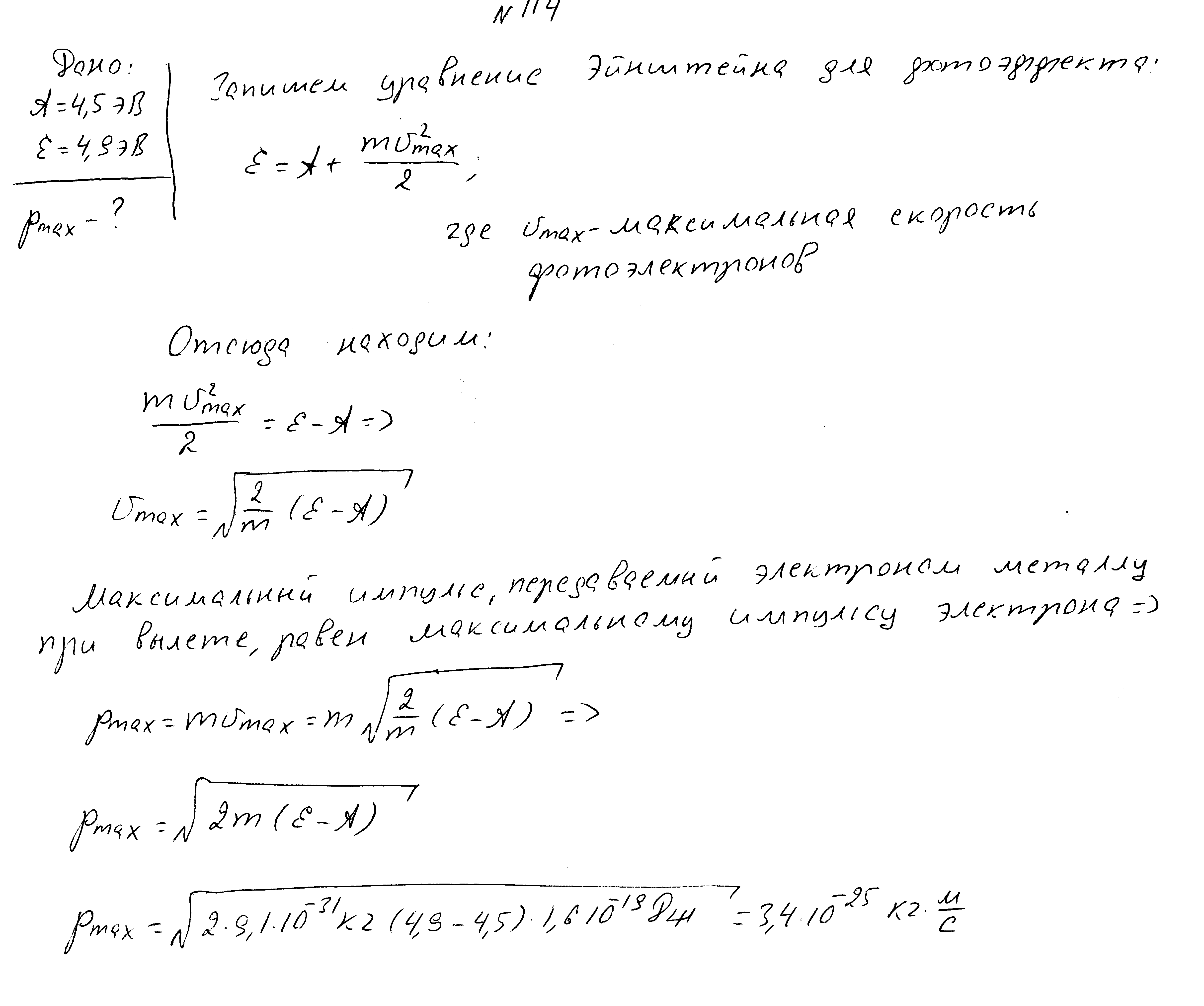
Красная граница фотоэффекта 2900 ангстрем, максимальная скорость фотоэлектронов 10 8 м/с. Найти отношение работы выхода электронов к энергии палающих фотонов.
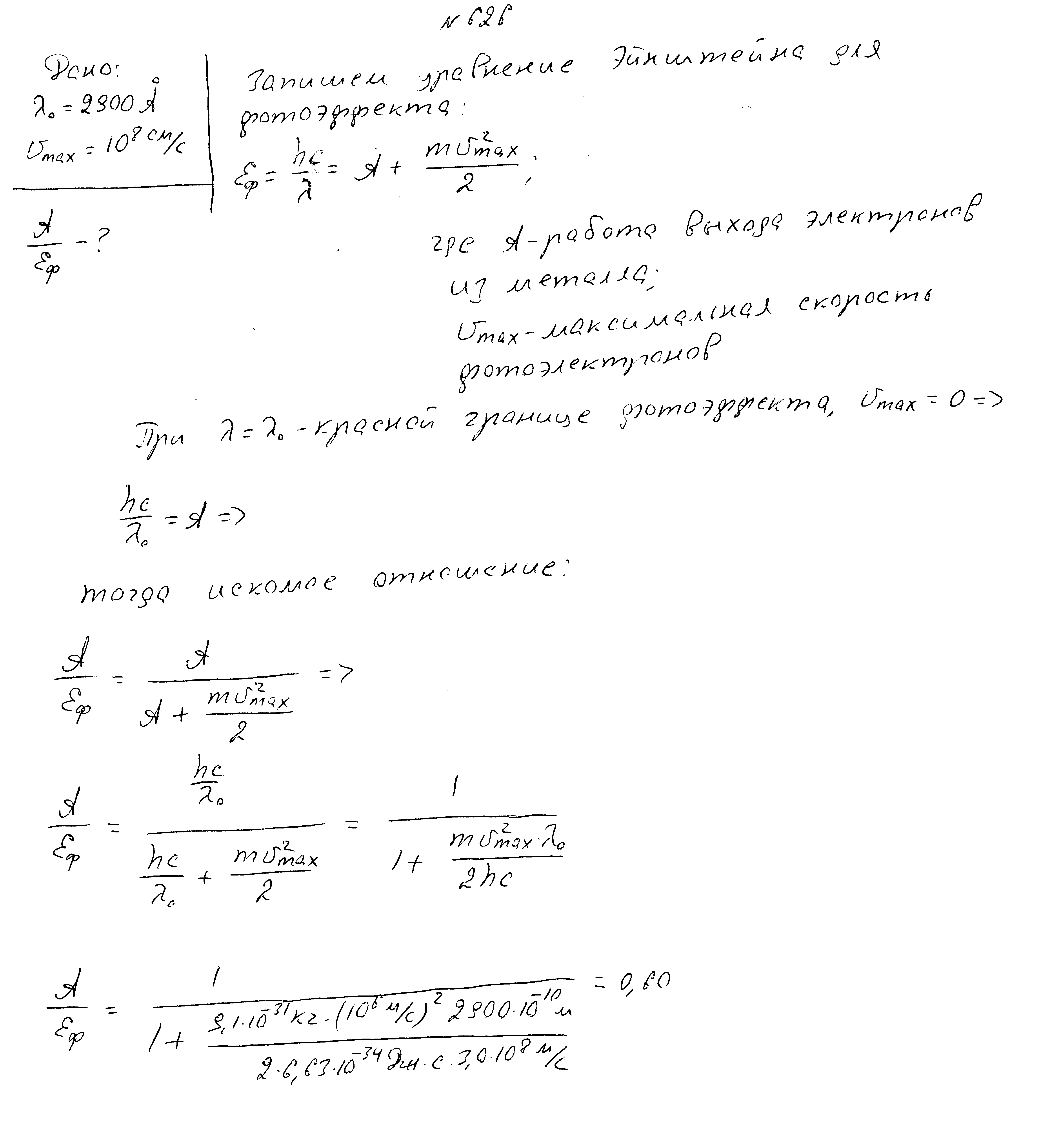
Длина волны падающего света 400нм, красная граница фотоэффекта равна 400нм. Чему равна максимальная скорость фотоэлектронов?
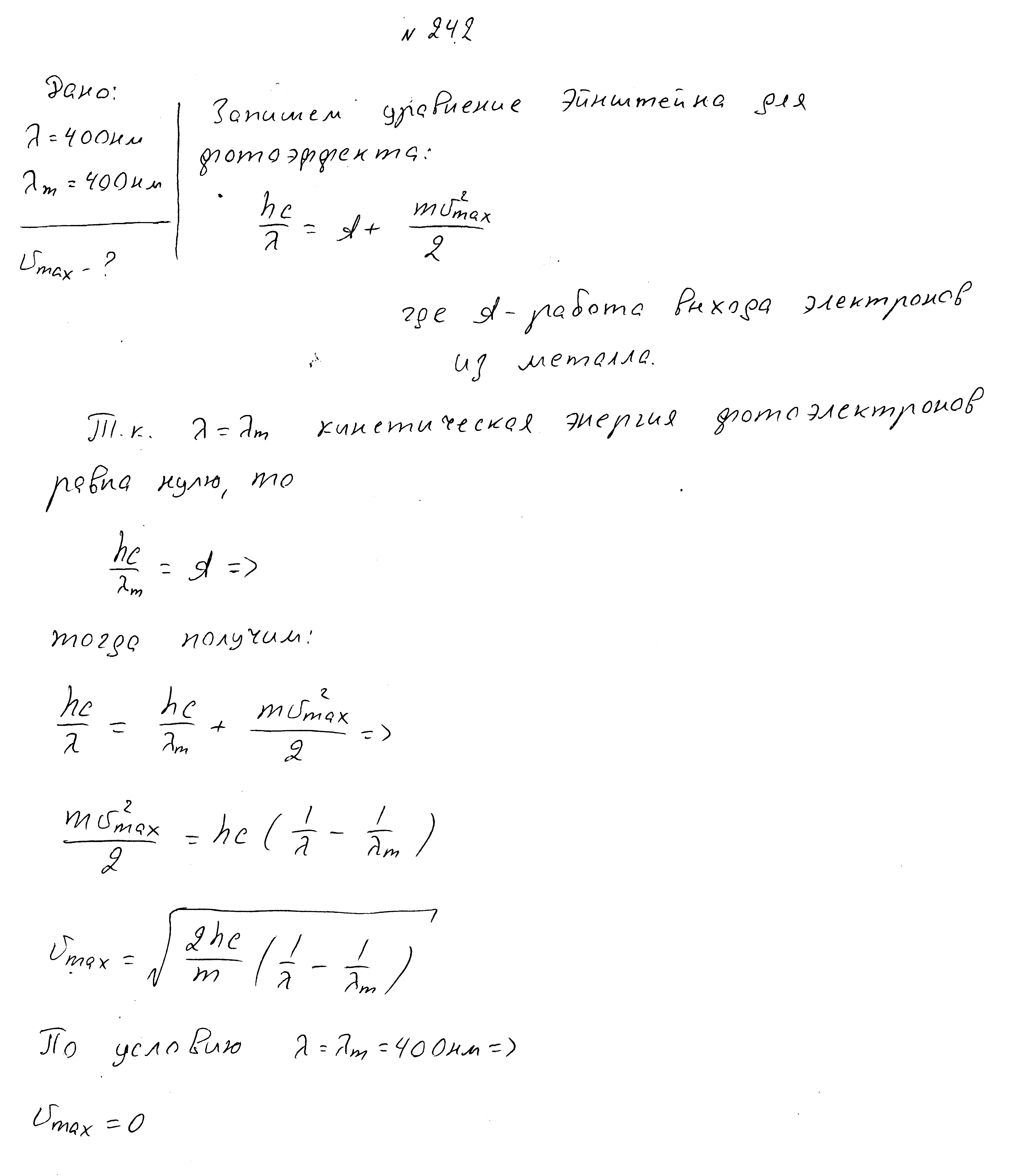
Длина волны падающего света 300нм, работа выхода электронов 3,74 эВ. Напряженность задерживающего электростатического поля 10 В/см.Какой максимальный путь фотоэлектронов при движении в направлении задерживающего поля?
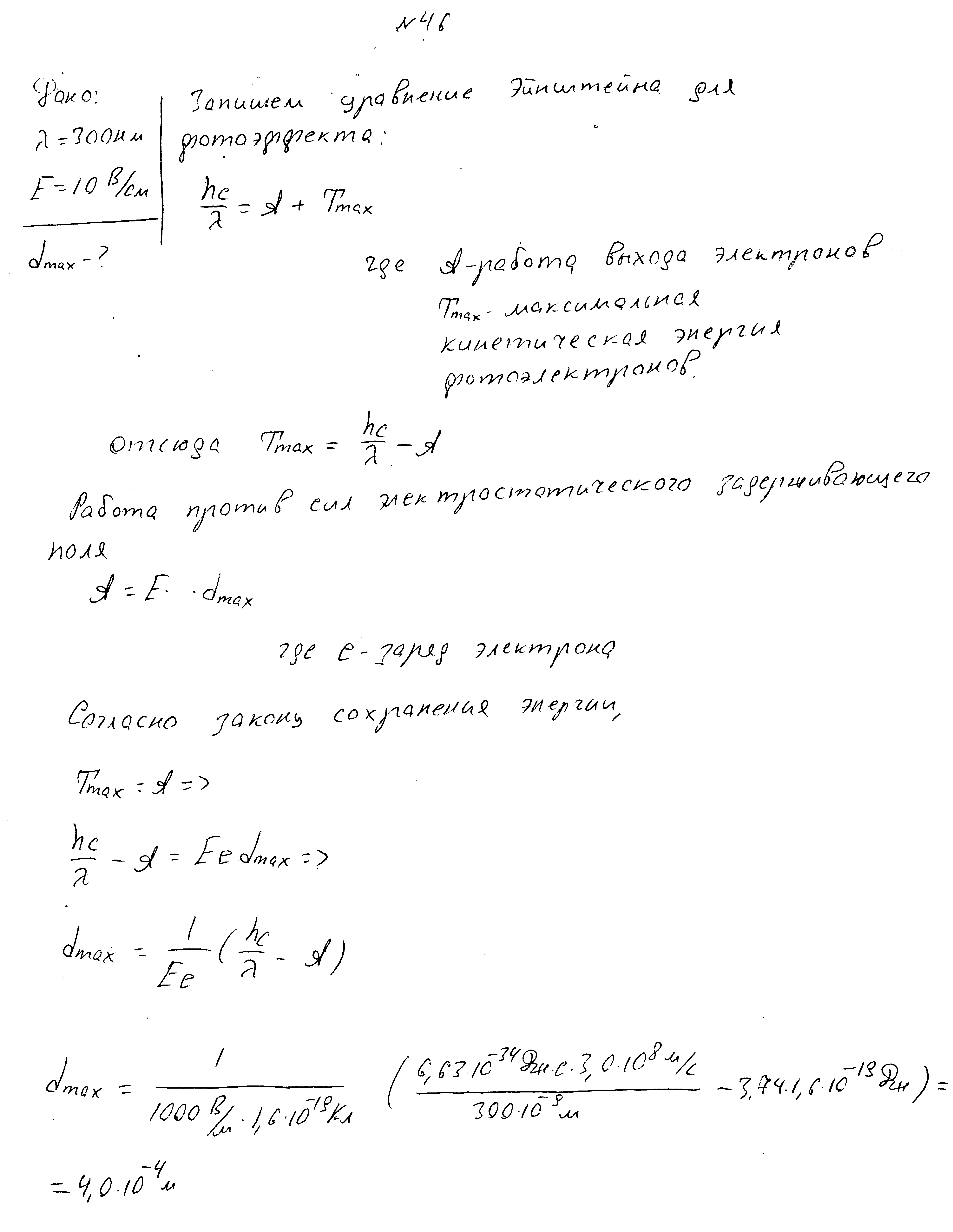
Длина волны падающего света 100 нм, работа выхода электронов 5,30эВ. Найти максимальную скорость фотоэлектронов.
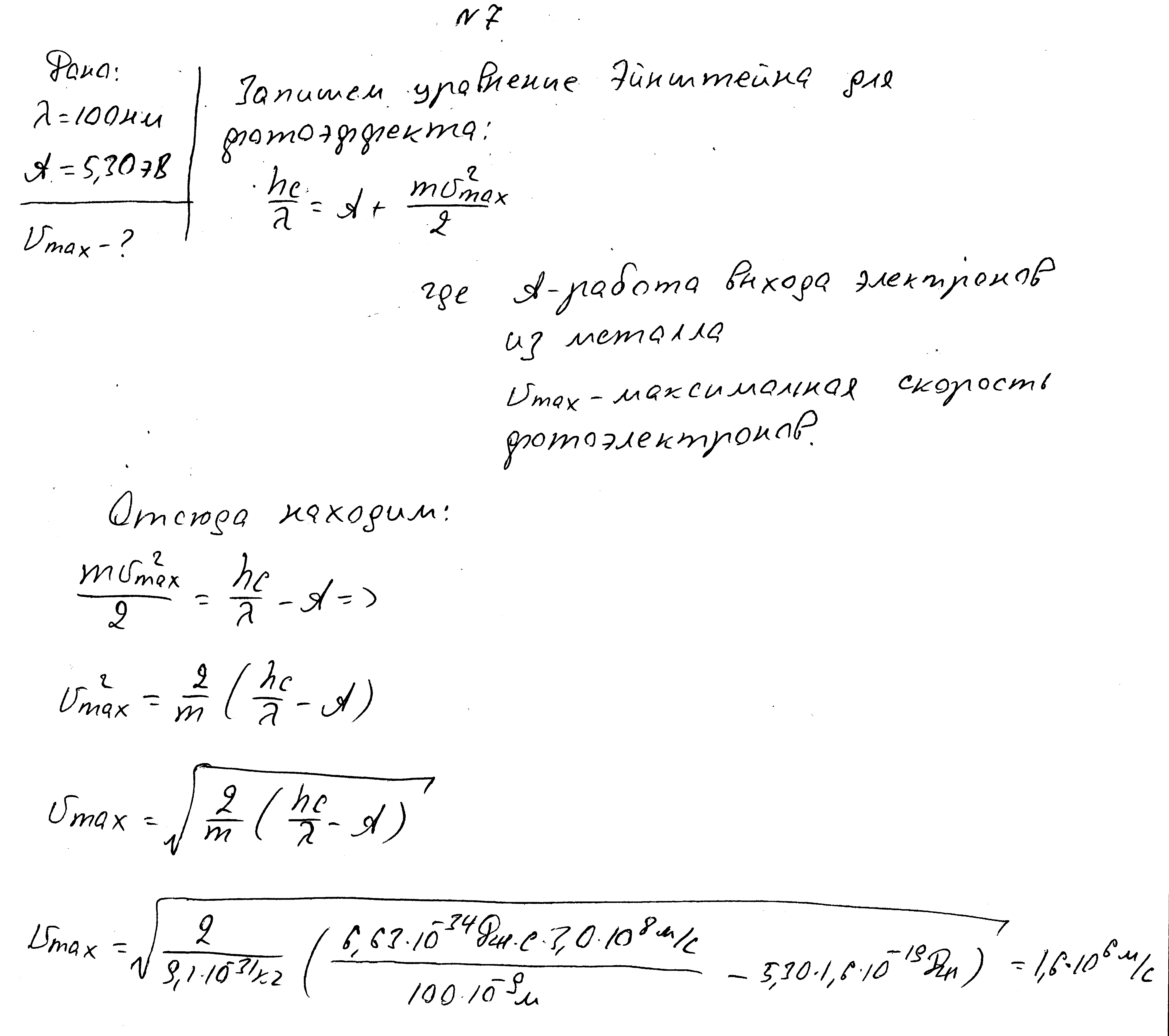
При длине волны радающего света 491нм задерживающая разность потенциалов 0,71В. Какова работа выхода электронов? Какой стала длина волны света, если задерживающая разность потенциалов стала равной 1,43В?
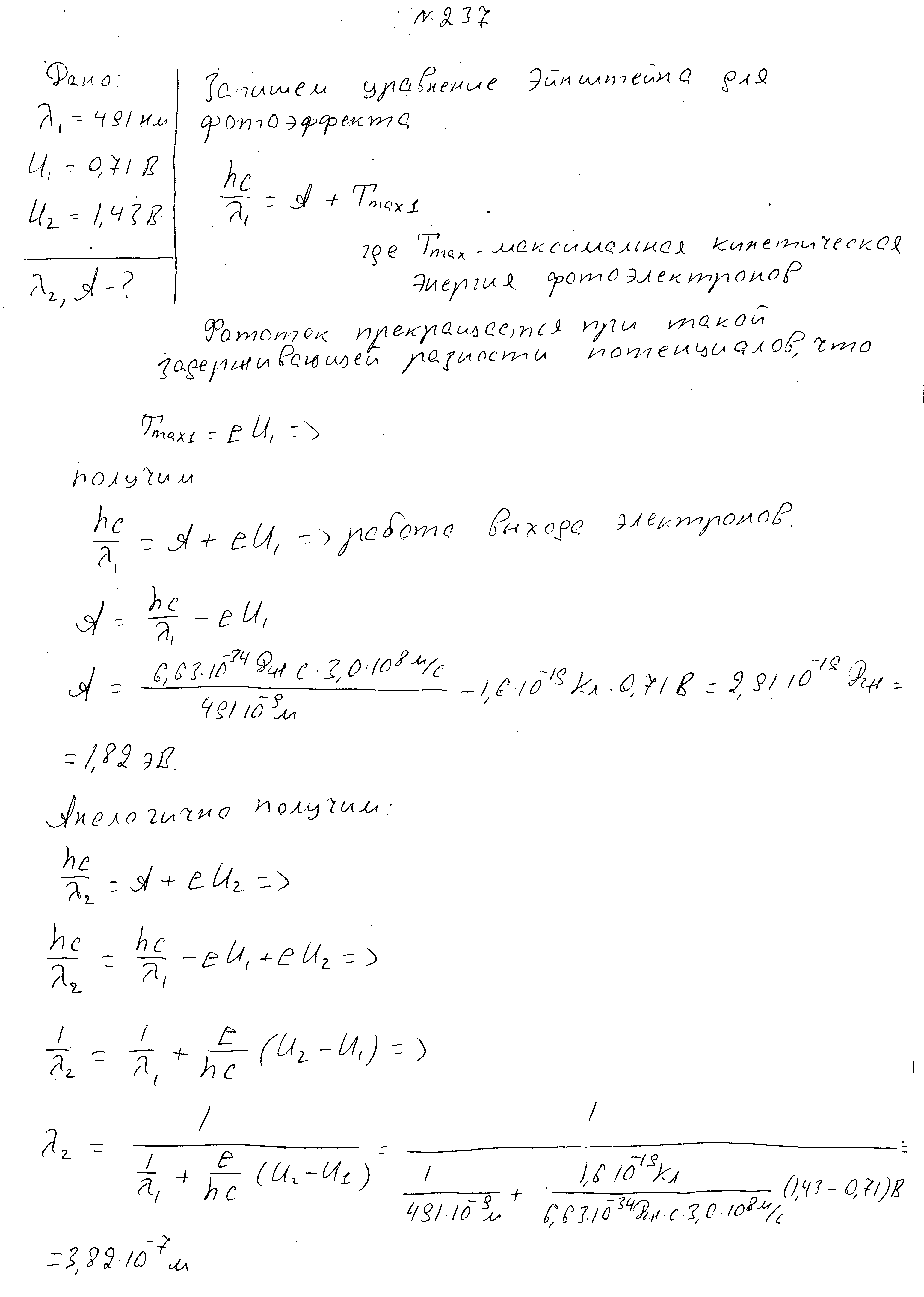
Кинетическая энергия фотоэлектронов 2,0 эВ, красная граница фотоэффекта 3,0*10 14 Гц. Определить энергию фотонов.

Красная граница фотоэффекта 0,257 мкм, задерживающая разность потенциалов 1,5В. Найти длину волны падающего света.
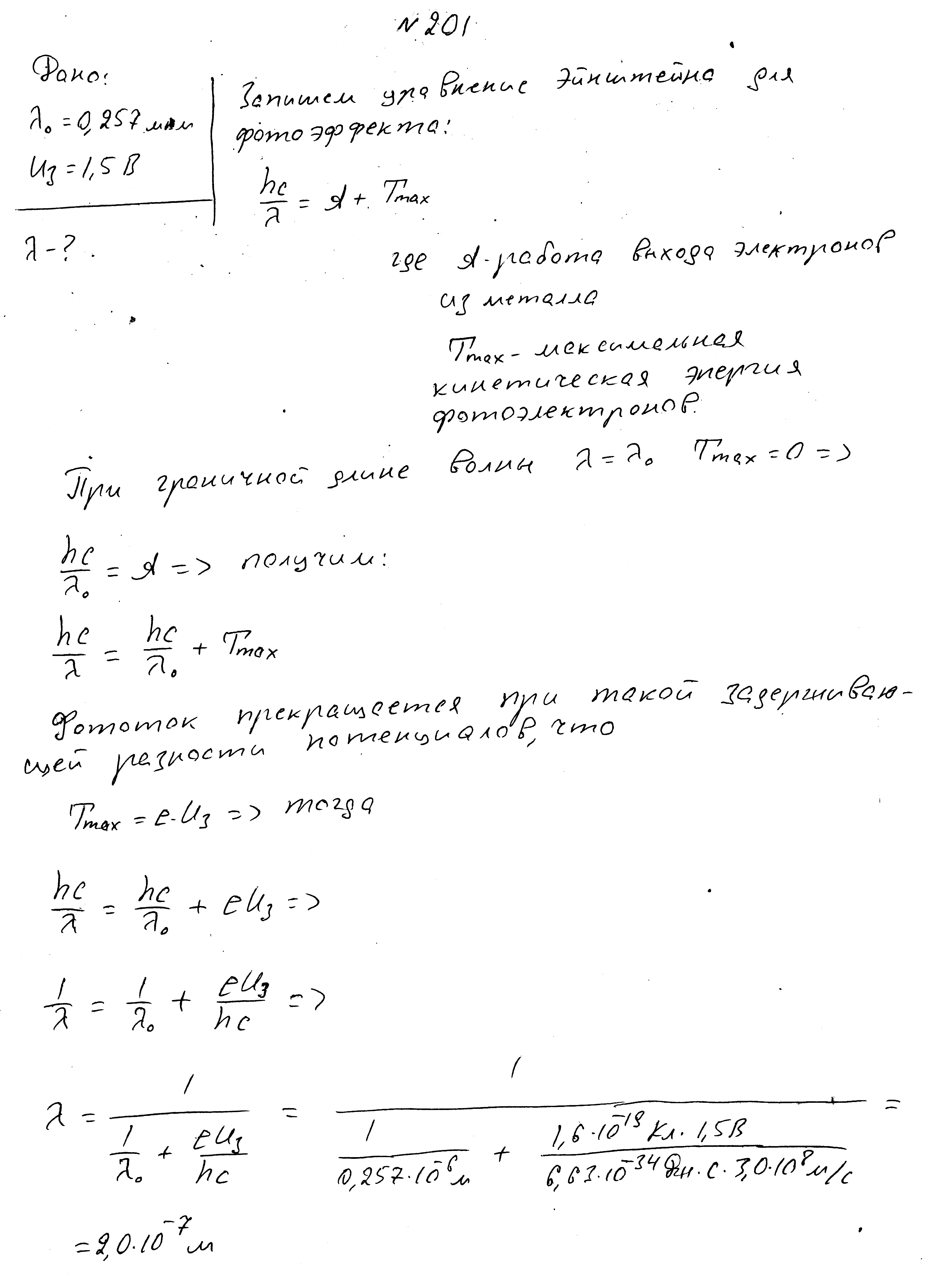
Красная граница фотоэффекта 2850 ангстрем. Минимальное значение энергии фотона, при котором возможен фотоэффект?

Ниже вы можете посмотреть обучаюший видеоролик на тему фотоэффекта и его законов.
Работа выхода электронов из металла. Контактные явления
Электроны проводимости в кристалле находятся в потенциальной яме. Выход из нее требует совершения работы по преодолению силы, действующей на электрон со стороны кристалла. Найдем эту силу. Обладая энергией теплового движения, электроны могут выскакивать из кристалла на расстояние в несколько периодов. Вышедший из кристалла и находящийся у его поверхности на расстоянии х электрон индуцирует в металле заряд е+ (рис.97). Этот наведенный заряд действует на вышедший электрон так, как если бы он был сосредоточен под поверхностью металла на глубине х в точке, симметричной той, в которой находится электрон (см. Эл-во §5). Индуцированный заряд е+ называется электрическим изображением заряда е-. Оба точечные заряда притягиваются друг к другу с силой Кулона . (14.1)
Но это и есть сила притяжения металлом вышедшего из него электрона. Под действием этой силы электрон втягивается обратно в металл. Чтобы удалить электрон из металла, надо совершить работу по преодолению этой силы, перемещая электроны на бесконечность из точки, расположенной на расстоянии х0 от поверхности металла. В качестве х0 можно взять межатомное расстояние.
На рис.98 показана зависимость потенциальной энергии электрона от расстояния х до атомной плоскости – стенки металла. Энергетическое расстояние еj от уровня Ферми до нулевого уровня называют термодинамической работой выхода электрона, величину j – потенциалом выхода. Уровень Ес обозначает дно зоны проводимости, где Е = 0. У металлов работа выхода еj заключена в пределах 1,8 ¸ 5,3 эВ. Меньше всего она у щелочных металлов, больше – у золота, серебра, платины (табл. 14.1).
| Таблица 14.1 | |||
| Металл | еj, эВ | Металл | еj, эВ |
| Литий Li | 2,38 | Платина Pt | 5,32 |
| Натрий Na | 2,35 | Ванадий V | 4,58 |
| Калий К | 2,22 | Вольфрам W | 4,54 |
| Рубидий Rb | 2,16 | Золото Au | 4,30 |
| Цезий Cs | 1,18 | Серебро Ag | 4,30 |
Большое влияние на работу выхода оказывают мономолекулярные адсорбированные слои. Например, слой атомов цезия Cs на вольфраме W (рис.99). Цезий щелочной металл. Его внешний, валентный электрон связан с ядром значительно слабее, чем валентные электроны в вольфраме. Поэтому атомы цезия отдают вольфраму свои валентные электроны и превращаются в положительные ионы. Между этими ионами и их электрическими изображениями в вольфраме возникает сила притяжения, удерживающая ионы цезия на поверхности вольфрама. Поле этого двойного электрического слоя помогает выходу электронов из вольфрама. По этому в присутствии слоя цезия работа выхода электрона из вольфрама уменьшается с 4,54 эВ до 1,38 эВ. Подобно цезию действуют одноатомные слои бария Ba, церия Cе, тория Th и др.
2. Термоэлектронная эмиссия.
С повышением температуры металла поверхность Ферми разрыхляется, энергия электронов увеличивается, и они поднимаются на более высокие уровни (рис.100). Соответственно уменьшается работа выхода электронов. Поэтому концентрация вылетевших из кристалла электронов в пристеночном слое растет. Процесс испускания электронов нагретым металлом называется термоэлектронной эмиссией.
Формально термоэлектронная эмиссия есть всегда, когда Т > 0 К. Но заметной она становится при температурах Т > 800 К.
Облако термоэлектронов находится в динамическом равновесии. Число вылетевших из металла электронов в каждый промежуток времени примерно равно числу электронов, втянутых в металл. Поэтому суммарный ток эмиссии равен нулю.
На основе термоэлектронной эмиссии построен ламповый вакуумный диод (рис.101). Здесь К – катод, обычно нагреваемая вольфрамовая спираль, А – анод, холодная металлическая пластина обычно цилиндрической формы. По оси этого цилиндра натягивается спираль катода. Оба электрода помещаются в стеклянный сосуд с высоким вакуумом.
Если между катодом и анодом создавать электрическое поле с напряжением U, как показано на рис.101, то термоэлектроны под действием этого поля будут перемещаться от катода к аноду. Возникает электрический ток в вакууме. Вольтамперная характеристика вакуумного диода показана на рис.102. С повышением анодного напряжения U ток I через анод растет почти пропорционально U. Но при достижении некоторого значенья Iнас перестает увеличиваться. Это предельное значение Iнас называют ток насыщением. Он возникает тогда, когда все электроны, вылетевшие из нагретого катода, захватываются полем и переносятся к аноду.
С повышением температуры катода ток насыщения увеличивается. Разделив ток насыщения на поверхность S катода, получаем плотность тока насыщения jнас = iнасçS. В 1901г. Оуэн Ричардсон, исходя из классических представлений, теоретически нашел зависимость плотности тока насыщения от температуры поверхности катода. Уточненная Дешманом в 1923г. с учетом квантовых представлений, зависимость jнас(Т) имеет вид: . Формула Ричардсона-Дэшмана (14.2)
Здесь еj – работа выхода, А – константа, имеющая разное значение у разных металлов и колеблющаяся около теоретического значения А= 1,2·10 6 Аç(м 2 К 2 ).
3. Контактная разность потенциалов.
Рассмотрим процессы, происходящие при контакте двух разных металлов. Допустим, до электрического контакта металл 1 (на рис.103 слева) имеет работу выхода еj1, а работа выхода металла 2 больше, j2 > j1.
Приведем металлы в состояние электрического контакта, то есть сблизим их до такого расстояния, при котором возможен эффективный обмен электронами. Поскольку работа выхода электронов из металла 2 больше, то уровень Ферми в металле 2 ниже, чем в металле 1. В результате электроны проводимости с уровня Ферми металла 1 начинают переходить на уровень Ферми металла 2.
В результате такого перехода электронов металл 2 заряжается отрицательно, энергия электронов и, соответственно, уровень Ферми в нем повышаются. Металл 1 заряжается положительно, энергия электронов и уровень Ферми в нем понижаются. Между металлами возникает контактная разность потенциалов j12.
Суммарное перетекание зарядов прекратится, когда уровни Ферми сравняются, а разность потенциалов между проводниками будет равна разности потенциалов выхода, j12 = j2 - j1, и встречные потоки электронов сравняются n21=-n12 (рис.103 справа). Контактная разность потенциалов между проводниками создает для электронов, переходящих в проводник с большей работой выхода, потенциальный барьер высотой еj12.
Оценим количество электронов, перетекающих из одного металла в другой при возникновении контактной разности потенциалов j12. Будем считать, что между контактирующими металлами остается зазор шириной d, а заряды концентрируются на контактирующих поверхностях. Тогда заряд Q на каждой из поверхностей, необходимый для создания напряжения j12, найдется из формулы плоского конденсатора, . (14.3)
Как видно из таблицы 14.1, контактная разность потенциалов В. Расстояние d между металлами не может быть меньше параметра решетки а » 0,3 нм. Полагая j12 =1 В и d = 0,3 нм, получаем максимальную плотность заряда на контактирующих поверхностях.
Разделив на заряд электрона получаем, что на 1 м 2 поверхности приходится 2·10 17 электронов. Если диаметр атомов взять равным постоянной решетки а = 0,3 нм, то на 1 м 2 поверхности в одноатомном слое металла размещается атомов. Если атомы металла содержат по одному валентному электрону, то для создания контактной разности потенциалов 1 В потребовалось всего лишь (2×10 17 ç10 19 )´100% = 2% электронов проводимости одноатомного поверхностного слоя.
4. Закон Вольта.
Контактную разность потенциалов открыл в девяностых годах XVIII века итальянец Александр Вольта. В серии экспериментов 1792–1794 годов он установил, что в цепочке из ряда последовательно соединенных металлов контактная разность потенциалов зависит лишь от крайних металлов. Этот опытный факт называется законом Вольта. Действительно, пусть имеется цепочка из металлов 1,2,3,4 (рис.104). Работа выхода металлов еj1, еj2, еj3, еj4. На границе каждой пары возникает контактная разность:
Просуммировав левые и правые части, получаем: . (14.5)
Сумма всех контактных ЭДС (левой части равенства) равна контактной ЭДС крайних металлов в цепочке (правая часть равенства). Если концы цепи замкнуть, то независимо от количества звенев сумма контактных разностей потенциалов равна нулю. Тока в цепи нет.
5. Термо-ЭДС.
Сумма контактных разностей потенциалов в замкнутой цепи равна нулю лишь при условии, что температуры всех контактов одинаковы. В 1821 г. Томас Зеебек, сжимая концы висмутовой и медной пластинок теплыми пальцами обнаружил, что если цепь замкнута, то в ней протекает ток. Это явление возникновения ЭДС в цепи из разных металлов при перепаде температур между спаями называют эффектом Зеебека или термоэлектричеством. В рамках классической электронной теории можно дать простое толкование явлению Зеебека и получить зависимость термо-ЭДС от перепада температур.
Пусть имеется замкнутая цепь из двух металлов 1 и 2 со спаями A и B (рис.105). Полагаем, что электроны проводимости на верхних уровнях зоны проводимости распределяются в силовом поле решетки по закону Больцмана.
Здесь n01 и n02 – концентрация электронов проводимости на уровнях Ферми. В силу полной заполняемости этих уровней будем полагать n01 = n02; U1 и U2 – потенциальная энергия электронов в металлах 1 и 2. Она может изменяться от нуля на уровне Ферми до еj (работа выхода) на нулевом уровне. Разделим первое уравнение на второе.
Разделив разность U1 –U2 на заряд электрона е, получаем концентрационную разность потенциалов между металлами 1 и 2. . (14.9)
Если температуры спаев ТА и ТB одинаковы, то концентрационная ЭДС в замкнутой цепи, так же, как контактная разность потенциалов, равна нулю. Тока в цепи нет. Если же температуры спаев разные, ТА ¹ ТB, то в цепи возникает термо-ЭДС (рис.106). Концентрационные перепады потенциалов в контактах А и B разные.
Учитывая грубость классических приближений, обычно выделяют лишь температурную зависимость, которая хорошо подтверждается опытом при малых перепадах температур, . (14.12)
Термо-ЭДС, возникающая в цепи из разных металлов, широко применяется для измерения температур в диапазоне от 0 К до » 1000°С. Соответствующее устройство из двух разных металлов называется термопарой. Один спай термопары поддерживается при постоянной температуре, например при 0 о С в сосуде с тающим льдом, другой помещают в ту среду, температуру которой хотят измерить. О величине температуры можно судить как по величине термотока, измеряемого гальванометром, так и более точно по величине термо-ЭДС, измеряемой методом компенсации. С помощью термопар можно измерять температуру с точностью до сотых долей градуса.
6. Эффект Пельтье,1834 г.
Он обратен эффекту Зеебека и состоит в том, что при пропускании тока по цепи из разных металлов один контакт у металла нагревается, другой охлаждается.
Пусть в цепи из двух разных металлов действует источник тока – батарея Б. В результате в цепи идет постоянный ток I (рис.107). Проходя спай B, электроны, идущие по цепи на рисунке против часовой стрелки, дополнительно ускоряются полем контактного потенциала. Их скорость дрейфа увеличивается, поэтому при столкновении с узлами электроны передают им большую, по сравнению со средней, энергию. Спай В нагревается больше, чем рядом расположенные участки проводников.
В спае А электроны тормозятся контактным полем, их скорость дрейфа уменьшается, поэтому спай А нагревается меньше, чем рядом расположенные участки проводов. Кроме того, для установления равновесия этих электронов с электронным газом им необходимо приобрести еще энергию. Эту энергию они черпают из решетки. В результате спай А охлаждается больше, чем нагревается. В итоге теплота в спае А поглощается.
Выделяющаяся или поглощающаяся теплота Пельтье QП в контакте пропорциональна заряду It, прошедшему через контакт. . (14.13)
Здесь П – коэффициент Пельтье связан с дифференциальной термо-ЭДС соотношением: П = аDT.(14.14)
Где DТ – разность температур между контактами.
Эффект Пельтье позволяет создавать малогабаритные холодильные устройства. Их особенность в том, что изменяя направление тока в цепи, можно один и тот же контакт заставить как поглощать тепло (холодильник), так и выделять его (нагреватель).
7. Эффект Томсона.
В 1853 – 54 г.г. Рудольф Клаузиус и Уильям Томсон независимо друг от друга применили к явлениям термоэлектричества принципы термодинамики. В процессе построения термодинамической теории термоэлектричества Томсон установил, что неравномерно нагретый проводник должен вести себя как система находящихся в контакте физически разнородных участков. На этом основании Томсон пришёл к заключению и подтвердил его экспериментально, что в однородном неравномерно нагретом проводнике должно выделяться или поглощаться тепло Пельтье (тепло Томсона). Само явление назвали эффектом Томсона.
Принципиальная схема экспериментальной установки изображена на рис.108
Концы двух одинаковых проводящих стержней помещены в два термостата с разными температурами Т1 и Т2. Допустим, Т1 > Т2. Тогда градиент температуры в верхнем стержне направлен по току I, а в нижнем – против тока. В результате в одном стержне выделяется тепло Томсона (его температура выше), а в другом – поглощается.
Знак эффекта у разных проводников разный. В висмуте и цинке, например, тепло выделяется, если поток тепла и электрический ток совпадают по направлению (на рисунке нижний проводник). А в Fe, Pt, Sb при тех же условиях тепло поглощается. С изменением направления тока знак эффекта во всех проводниках меняется.
Тепло Томсона Q, выделяющееся в проводнике, пропорционально перепаду температур ΔТ, току I, протекающему по проводнику, и времени t Q = σΔTIt.
Здесь σ – коэффициент Томсона. Он зависит от материала провода и от его температуры. Коэффициент σ невелик. У металлов он порядка 10 –5 ВçК. За положительное направление тока принимают направление градиента температур, то есть направление от холодного конца проводника к горячему. Если тепло при этих условиях выделяется (проводник нагревается), эффект Томсона считается положительным.
Количественно эффект Томсона исследовал в 1867 г. Франсуа Леру. В установке, собранной по схеме рис. 108, к поверхности стержней он присоединял спаи термопар. Пока тока через стержни не было, термоЭДС в цепи термопар была равна нулю. При включении тока через стержни появлялась термоЭДС, величина и знак которой позволяли определить коэффициент Томсона σ.
8. Закон Джоуля – Ленца в замкнутой цепи всегда выполняется. Суммарный эффект Пельтье и Томсона в замкнутой цепи равен нулю, поскольку наряду с участками цепи, где тепло Пельтье и Томсона выделяется, всегда есть участки, где такое же тепло поглощается.
Работа выхода электронов из металла. Термоэлектронная эмиссия
Электроны проводимости в металлах образуют своеобразный электронный газ и участвуют в тепловом движении. Но поскольку они удерживаются в объеме металла, а не разлетаются из него, значит, вблизи поверхности металла существуют силы, действующие на электроны и направленные внутрь металла. Для того чтобы электрон вывести за пределы металла необходимо совершить определенную работу против удерживающих его сил.
Работой выхода А электрона из металла называется работа, которую нужно совершить при удалении электрона из металла в вакуум.
Электрон – заряженная частица и сила, препятствующая его выходу из металла, имеет электрическую природу. Существуют две наиболее вероятные причины возникновения этой силы, а следовательно, и работы выхода.
Электрон, обладая достаточной кинетической энергией, может покинуть поверхность металла. На поверхности металла в результате этого индуцируется положительный заряд, отчего между электроном и металлом возникает сила притяжения, препятствующая удалению электрона. Работа этой силы представляет часть работы выхода.
Электроны вследствие хаотического движения способны пересекать поверхность металла и удаляться от нее на малые расстояния. При этом число электронов, покидающих поверхность металла, равно числу электронов, возвращающихся в металл и на границе металл-вакуум поддерживается динамическое равновесие электронов.
Над поверхностью металла, таким образом, существует электронная “атмосфера “ т.е. у поверхности образуется как бы двойной электрический слой (напоминающий плоский заряженный конденсатор. Рис.97)
Электрическое поле такого двойного электрического слоя заключено в малом зазоре над поверхностью металла, и прохождение электрона через этот двойной электрический слой сопровождается совершением определенной работы, связанной с разностью потенциалов А = е φ. Величину φ называют потенциальным барьером. Полная работа выхода электрона обуславливается обеими этими причинами.
Если электрон внутри металла имеет кинетическую энергию
то он может покинуть объем металла. Работа выхода для металлов имеет порядок величины несколько эВ. Энергия же теплового движения электронов в металле при комнатной температуре (Т ≃ 300 0 К) имеет величину порядка ∼ 0,03 эВ. Поэтому подавляющее большинство электронов будет связано в пределах металла. Однако, если электронам сообщить дополнительную энергию, то часть из них получает возможность покинуть металл и мы наблюдаем явление испускания электронов, называемое электронной эмиссией. Различают различные типы электронной эмиссии. Если электроны получают энергию за счет тепловой энергии при повышении температуры, то такая эмиссия называется термоэлектронной.
При подведении энергии светом наблюдается фотоэмиссия, при бомбардировке поверхности какими-либо частицами наблюдается вторичная электронная эмиссия. Эмиссия под действием сильного электрического поля называется автоэлектронной.Термоэлектронную эмиссию можно наблюдать на электронной лампе – электровакуумном диоде (рис. 98), состоящим из анода А и накаливаемого катода К, включенных в электрическую цепь. Ток диода (анодный ток) имеет зависимость “степени 3/2”
I = c· U 3/2 , где U – анодное напряжение; с – const.
Плотность тока насыщения, когда все вылетающие с катода электроны (при данной температуре катода) достигают анода, определяют по формуле Ричардсона-Дэшмана
где А – постоянная Ричардсона-Дэшмана =6,02·10 5 А/м 2 ·К 2 , Т – абсолютная температура катода, – работа выхода материала катода, k – постоянная Больцмана.
Электрический ток в газах
Газы, состоящие из нейтральных молекул и атомов, не проводят электрический ток. Для возникновения электропроводности газов они должны быть ионизированы.
Ионизацией молекулы или атома называется процесс отщепления или отрыва от них одного или нескольких электронов в результате чего возникают положительный ион и электроны. Если нейтральный атом и молекула присоединяют электрон, то возникает отрицательный ион. Процесс, обратный ионизации, т.е. такой, при котором электроны, присоединяясь к положительному иону, образуют нейтральную молекулу или атом, называется рекомбинацией.
Для ионизации молекулы (атома) небходимо совершить работу ионизации Аi против сил притяжения между вырываемым электроном и атомным остатком. Эта работа зависит от вида атома, кратности ионизации, энергетического состояния. Потенциалом ионизации φi называется разность потенциалов в ускоряющем поле, которую должна пройти заряженная частица, чтобы накопить энергию, равную работе ионизации
Ионизация газов вызывается бомбардировкой его атомов и молекул заряженными частицами (электронами, ионами, α-частицами), нейтронами, электромагнитным излучением.
Газовым разрядом называется процесс прохождения электрического тока через газ. Различают самостоятельный и несамостоятельный газовые разряды. Предположим, что на газовый промежуток действует какой-либо ионизатор (например, ультрафиолетовые или рентгеновские лучи, падающие на катод и выбивающие из него фотоэлектроны), в результате чего газ становится электропроводящим и в цепи потечет ток (рис. 99а). Увеличение анодного напряжения приведет к изменению тока в цепи. Вольтамперную характеристику можно разделить на 4 участка (рис. 99б). На первом участке кривой при небольших напряжениях выполняется закон Ома. Плотность тока в газовом промежутке равна
где n0 – число пар противоположно заряженных частиц в единице объема; u+ и u- - подвижность этих частиц;
е – заряд электрона;
Е – напряженность поля.
На 2-м участке кривой наблюдается отклонение от закона Ома, вызванное убыванием концентрации ионов в газе и ток достигает насыщения IН при некотором значении UН. Увеличение напряжения на участке 3 кривой не приводит к увеличению тока, т.е. все образующиеся в газе электроны и ионы достигают анода и катода.
Газовый разряд, который поддерживается вследствие действия внешнего ионизатора, получил название несамостоятельного.
Если в одном из режимов разряда на участках кривой 1-2-3 действие внешнего ионизатора прекратить, то разряд прекратится. Дальнейшее увеличение анодного напряжения приводит к резкому возрастанию анодного тока. Это происходит вследствие того, что электроны под действием поля приобретают энергию, достаточную для ионизации молекул и атомов газа. Процесс такой ионизации носит лавинный характер.
За время свободного пробега в сильном электрическом поле электрон(e) успевает приобрести энергию, достаточную для того, чтобы столкнувшись с молекулой(M), вызвать ее ионизацию.
При этом образуется положительный ион и добавочный электрон.
Эти два электрона в свою очередь набрав нужную энергию ионизируют два атома, а образовавшиеся (2+2) электрона ионизируют следующие 4 атома и удвоят количество электронов и т.д. Таким образом, происходит лавинообразное размножение первичных ионов, созданных внешним ионизатором, и усиление разрядного тока как показано на рис. 100.
Самостоятельным газовым разрядом называется электрический разряд в газе, который продолжается после прекращения действия внешнего ионизатора. Для существования самостоятельного газового разряда необходимо, чтобы электронные лавины поддерживали сами себя, т.е. чтобы в газе происходил еще и другой процесс, непрерывно воспроизводящий новые электроны взамен ушедших на анод.
Такими могут быть процессы вторичной электронной эмиссии с катода в результате его бомбардировки ускоренными положительными ионами, фотоэффект, соударения положительных ионов с нейтральными молекулами и атомами.
Виды газовых разрядов:
Тлеющий – наблюдаемый при давлениях 0,1 – 0,01 мм. рт. ст., применяется в газовых трубках, лампах дневного света ( красное свечение у неона, синевато-зеленое – у аргона, желтоватые – у натрия).
Искровой разряд – возникает между электродами при сильных полях – на воздухе Екрит ≃ 3·10 6 В/м или 30 кВ/см, в вакууме Екрит выше.
Коронный разряд – когда вследствие высокой напряженности на острие электрода начинает развиваться лавинный процесс, но вследствие снижения напряженности поля по мере удаления от острия эта лавина не достигает анода.
Молния – вид искрового разряда. Токи 10 4 - 5 ·10 5 А. ΔU 10 8 - 10 9 В, длительность мкс., заряд 0,1 – 200 Кл. Сильное разогревание воздуха приводит к возникновению ударной звуковой волны – грому.
Дуговой разряд – при низком сопротивлении цепи искровой разряд переходит в дуговой, который протекает при высоких токах в десятки и сотни ампер.
Читайте также:
