Какой тип проводимости в металлах

Обновлено: 08.01.2025

В этом листке мы приступаем к подробному изучению того, как осуществляется прохождение электрического тока в различных проводящих средах — твёрдых телах, жидкостях и газах.

Напомним, что необходимым условием возникновения тока является наличие в среде достаточно большого количества свободных зарядов, которые могут начать упорядоченное движение под действием электрического поля. Такие среды как раз и называются проводниками электрического тока.

Наиболее широко распространены металлические проводники. Поэтому начинаем мы с вопросов распространения электрического тока в металлах.

Мы много раз говорили о свободных электронах, которые являются носителями свободных зарядов в металлах. Вам хорошо известно, что электрический ток в металлическом проводнике образуется в результате направленного движения свободных электронов.

Свободные электроны

Металлы в твёрдом состоянии имеют кристаллическую структуру: расположение атомов в пространстве характеризуется периодической повторяемостью и образует геометрически правильный рисунок, называемый кристаллической решёткой.

Атомы металлов имеют небольшое число валентных электронов, расположенных на внешней электронной оболочке. Эти валентные электроны слабо связаны с ядром, и атом легко может их потерять.

Когда атомы металла занимают места в кристаллической решётке, валентные электроны покидают свои оболочки — они становятся свободными и отправляются «гулять» по всему кристаллу (а именно, свободные электроны перемещаются по внешним орбиталям соседних атомов. Эти орбитали перекрываются друг с другом вследствие близкого расположения атомов в кристаллической решётке, так что свободные электроны оказываются «общей собственностью» всего кристалла). В узлах кристаллической решётки металла остаются положительные ионы, пространство между которыми заполнено «газом» свободных электронов (рис. 1 ).

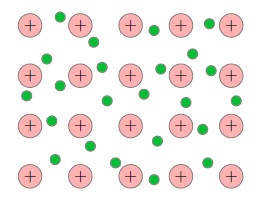
Рис. 1. Свободные электроны

Свободные электроны и впрямь ведут себя подобно частицам газа (другой адекватный образ — электронное море, которое «омывает» кристаллическую решётку) — совершая тепловое движение, они хаотически снуют туда-сюда между ионами кристаллической решётки. Суммарный заряд свободных электронов равен по модулю и противоположен по знаку общему заряду положительных ионов, поэтому металлический проводник в целом оказывается электрически нейтральным.

Газ свободных электронов является «клеем», на котором держится вся кристаллическая структура проводника. Ведь положительные ионы отталкиваются друг от друга, так что кристаллическая решётка, распираемая изнутри мощными кулоновскими силами, могла бы разлететься в разные стороны. Однако в тоже самое время ионы металла притягиваются к обволакивающему их электронному газу и, как ни в чём не бывало, остаются на своих местах, совершая лишь тепловые колебания в узлах кристаллической решётки вблизи положений равновесия.

Что произойдёт, если металлический проводник включить в замкнутую цепь, содержащую источник тока? Свободные электроны продолжают совершать хаотическое тепловое движение, но теперь — под действием возникшего внешнего электрического поля — они вдобавок начнут перемещаться упорядоченно. Это направленное течение электронного газа, накладывающееся на тепловое движение электронов, и есть электрический ток в металле (поэтому свободные электроны называются также электронами проводимости). Скорость упорядоченного движения электронов в металлическом проводнике, как нам уже известно, составляет приблизительно 0,1мм/с.

Опыт Рикке

Почему мы решили, что ток в металлах создаётся движением именно свободных электронов? Положительные ионы кристаллической решётки также испытывают на себе действие внешнего электрического поля. Может, они тоже перемещаются внутри металлического проводника и участвуют в создании тока?

Упорядоченное движение ионов означало бы постепенный перенос вещества вдоль направления электрического тока. Поэтому надо просто пропускать ток по проводнику на протяжении весьма длительного времени и посмотреть, что в итоге получится. Такого рода эксперимент и был поставлен Э.Рикке в 1901 году.

В электрическую цепь были включены три прижатых друг к другу цилиндра: два медных по краям и один алюминиевый между ними (рис. 2 ). По этой цепи пропускался электрический ток в течение года.

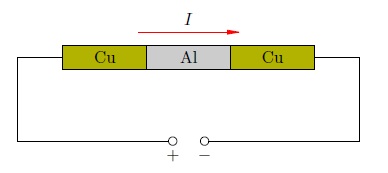
Рис. 2. Опыт Рикке

За год сквозь цилиндры прошёл заряд более трёх миллионов кулон. Предположим, что каждый атом металла теряет по одному валентному электрону, так что заряд иона равен элементарному заряду Кл. Если ток создаётся движением положительных ионов, то нетрудно подсчитать (сделайте это сами!), что такая величина прошедшего по цепи заряда соответствует переносу вдоль цепи около 2кг меди.

Однако после разъединения цилиндров было обнаружено лишь незначительное проникновение металлов друг в друга, обусловленное естественной диффузией их атомов (и не более того). Электрический ток в металлах не сопровождается переносом вещества, поэтому положительные ионы металла не принимают участия в создании тока.

Опыт Стюарта–Толмена

Прямое экспериментальное доказательство того, что электрический ток в металлах создаётся движением свободных электронов, было дано в опыте Т.Стюарта и Р.Толмена (1916 год).

Эксперименту Стюарта–Толмена предшествовали качественные наблюдения, сделанные четырьмя годами ранее русскими физиками Л.И.Мандельштамом и Н.Д.Папалекси. Они обратили внимание на так называемый электроинерционный эффект: если резко затормозить движущийся проводник, то в нём возникает кратковременный импульс тока. Эффект объясняется тем, что в течение небольшого времени после торможения проводника его свободные заряды продолжают двигаться по инерции.

Однако никаких количественных результатов Мандельштам и Папалекси не получили, и наблюдения их опубликованы не были. Честь назвать опыт своим именем принадлежит Стюарту и Толмену, которые не только наблюдали указанный электроинерционный эффект, но и произвели необходимые измерения и расчёты.

Установка Стюарта и Толмена показана на рис. 3 .

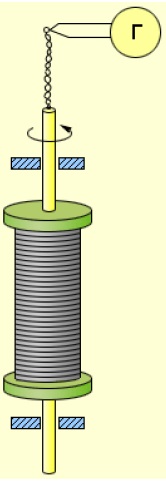
Рис. 3. Опыт Стюарта–Толмена

Катушка большим числом витков металлического провода приводилась в быстрое вращение вокруг своей оси. Концы обмотки с помощью скользящих контактов были подсоединены к специальному прибору — баллистическому гальванометру, который позволяет измерять проходящий через него заряд.

После резкого торможения катушки в цепи возникал импульс тока. Направление тока указывало на то, что он вызван движением отрицательных зарядов. Измеряя баллистическим гальванометром суммарный заряд, проходящий по цепи, Стюарт и Толмен вычислили отношение заряда одной частицы к её массе. Оно оказалось равно отношению для электрона, которое в то время уже было хорошо известно.

Так было окончательно выяснено, что носителями свободных зарядов в металлах являются свободные электроны. Как видите, этот давно и хорошо знакомый вам факт был установлен сравнительно поздно — учитывая, что металлические проводники к тому моменту уже более столетия активно использовались в самых разнообразных экcпериментах по электромагнетизму (сравните, например, с датой открытия закона Ома — 1826 год. Дело, однако, заключается в том, что сам электрон был открыт лишь в 1897 году).

Зависимость сопротивления от температуры

Опыт показывает, что при нагревании металлического проводника его сопротивление увеличивается. Как это объяснить?

Причина проста: с повышением температуры тепловые колебания ионов кристаллической решётки становятся более интенсивными, так что число соударений свободных электронов с ионами возрастает. Чем активнее тепловое движение решётки, тем труднее электронам пробираться сквозь промежутки между ионами (Представьте себе вращающуюся проходную дверь. В каком случае труднее проскочить через неё: когда она вращается медленно или быстро? :-)). Скорость упорядоченного движения электронов уменьшается, поэтому уменьшается и сила тока (при неизменном напряжении). Это и означает увеличение сопротивления.

Как опять-таки показывает опыт, зависимость сопротивления металлического проводника от температуры с хорошей точностью является линейной:

Здесь — сопротивление проводника при . График зависимости (1) является прямой линией (рис. 4 ).

Множитель называется температурным коэффициентом сопротивления. Его значения для различных металлов и сплавов можно найти в таблицах.

Длина проводника и его площадь поперечного сечения при изменении температуры меняются несущественно. Выразим и через удельное сопротивление:

и подставим эти формулы в (1) . Получим аналогичную зависимость удельного сопротивления от температуры:

Коэффициент весьма мал (для меди, например, ), так что температурной зависимостью сопротивления металла часто можно пренебречь. Однако в ряде случаев считаться с ней приходиться. Например, вольфрамовая спираль электрической лампочки раскаляется до такой степени, что её вольт-амперная характеристика оказывается существенно нелинейной.

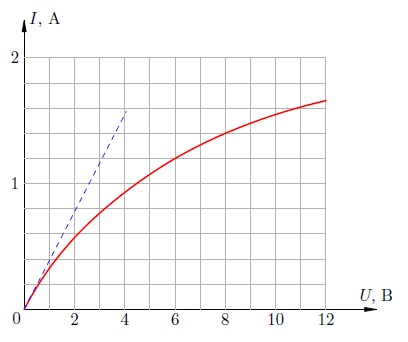
Рис. 5. Вольт-амперная характеристика лампочки

Так, на рис. 5 приведена вольт-амперная характеристика автомобильной лампочки. Если бы лампочка представляла собой идеальный резистор, её вольт-амперная характеристика была прямой линией в соответствии с законом Ома. Эта прямая изображена синим пунктиром.

Однако по мере роста напряжения, приложенного к лампочке, график отклоняется от этой прямой всё сильнее и сильнее. Почему? Дело в том, что с увеличением напряжения ток через лампочку возрастает и больше разогревает спираль; сопротивление спирали поэтому также увеличивается. Следовательно, сила тока хотя и продолжит возрастать, но будет иметь всё меньшее и меньшее значение по сравнению с тем, которое предписывается «пунктирной» линейной зависимостью тока от напряжения.

Электропроводность металлов

Электропроводность металлов и сплавов – физическое свойство, которое учитывается при производстве разных видов изделий. Например, для изготовления электрических кабелей, микросхем используют металлы с высокими показателями электропроводности.

Данный параметр зависит от факторов окружающей среды: температуры, давления, агрегатного состояния, наличия магнитных полей и т. д. Если говорить о чистых металлах и влиянии температуры на их электропроводность, то с ростом она падает. Подробнее о том, что собой представляет электропроводность металлов, вы узнаете из нашего материала.

Природа электропроводности металлов

Электропроводностью называют способность тела, вещества проводить ток. Кроме того, этим термином обозначается физическая величина, которая численно характеризует данную способность. Электропроводность металла определяется числом свободных ионов в проводнике – их движение и является электрическим током. Данный показатель исчисляется в сименсах, а в международной системе единиц для его обозначения используется буква «S».

В зависимости от того, какой электропроводностью обладают металлы и иные вещества, среди них выделяют проводники, диэлектрики и полупроводники. Правда, между данными группами практически не существует четкого разграничения.

Чем обусловлена высокая электропроводность металлов-проводников? Они имеют большое количество свободных ионов. Среди веществ этой группы выделяют два рода, исходя из физической природы протекания тока. К первому относятся металлы с электронной проводимостью, по которым ток проходит благодаря движению свободных электронов.

Ко второму причисляют растворы кислот, щелочей, солей или электролиты, имеющие ионную проводимость. Иными словами, здесь интересующий нас процесс связан с движением положительных и отрицательных ионов. Уровень электропроводности проводников превышает 106(Ом·м)-1.

VT-metall предлагает услуги:

Лазерная резка металла Гибка металла Порошковая покраска металла Сварочные работы

Диэлектрики обладают малым числом свободных ионов, поэтому отличаются низкой электропроводностью, практически не проводят ток. Такими материалами являются дерево, смолы, пластмассы, стекло, пр. Для них данный показатель составляет менее 106(Ом·м)-1.

По своим проводящим свойствам полупроводники занимают промежуточное положение между материалами описанных выше групп. К ним относятся германий, кремний, селен, прочие соединения, получаемые искусственно.

Существует зависимость электропроводности металлов и иных веществ от температуры, но она является индивидуальной для каждого материала. Повышение степени нагрева металлов приводит к сокращению времени свободного пробега электронов. Увеличение температуры влечет за собой возрастание тепловых колебаний кристаллической решетки, на которой рассеиваются электроны, что вызывает уменьшение электропроводности.

Полупроводникам свойственна другая зависимость электропроводности металлов от температуры: ее повышение провоцирует рост электропроводности, поскольку увеличивается число электронов проводимости и положительных носителей заряда. У диэлектриков электропроводность тоже может возрастать, однако для этого требуется очень высокое электрическое напряжение.

Металлы способны проводить ток, поскольку воздействие электромагнитного поля вызывает потерю связи между электроном и атомом из-за высокой степени ускорения.

Электрическое сопротивление металлов

Электрическое сопротивление является частью закона Ома и исчисляется в омах (Ом). Нужно понимать, что электрическое и удельное сопротивление являются разными явлениями. Если первое представляет собой свойство объекта, то второе характеризует материал.

Так, электрическое сопротивление резистора зависит от формы и удельного сопротивления материала, использованного для изготовления данного элемента электрической цепи.

Допустим, проволочный резистор состоит из длинной тонкой проволоки и обладает более высоким сопротивлением, чем аналогичный элемент, но выполненный из короткой и толстой проволоки. При этом оба они сделаны из одного металла.

Если сравнить два резистора из проволоки одинаковой длины и диаметра, то большим электрическим сопротивлением будет обладать тот, который состоит из материала с высоким удельным сопротивлением. А его аналогу из материала с низким удельным сопротивлением будет свойственно меньшее электрическое сопротивление.

В этом случае работает тот же принцип, что и в гидравлической системе, прокачивающей воду по трубам:

Чем больше длина трубы и меньше ее толщина, тем с более высоким сопротивлением сталкивается жидкость.
Вода будет испытывать на себе меньшее сопротивление в пустой трубе, чем в заполненной песком.

Под удельным сопротивлением понимают способность материала препятствовать прохождению электрического тока. В физике существует и обратная величина, известная как проводимость. Она выглядит таким образом:

Σ = 1/ρ, где ρ – удельное сопротивление вещества.

Электропроводность металлов и других веществ зависит от свойств носителей зарядов. В металлах присутствуют свободные электроны – на внешней оболочке их число доходит до трех. Во время химических реакций с элементами из правой части таблицы Менделеева атом металла отдает их. С электропроводностью чистых металлов все несколько иначе. В их кристаллической структуре эти наружные электроны общие и переносят заряд под действием электрического поля.

В случае с растворами в качестве носителей заряда выступают ионы.

Степень электропроводности разных металлов и сплавов

Развитием электронной теории электропроводности металлов занимался немецкий физик Пауль Друде. Именно благодаря его исследованиям стало известно о сопротивлении, наблюдаемом при прохождении электрического тока через проводник. В результате удалось разделить вещества на группы, исходя из степени их проводимости.

Данная информация необходима, например, чтобы выбрать наиболее подходящий металл для производства кабеля, обладающего определенным набором свойств. Ошибка в этом случае чревата перегревом под действием тока избыточного напряжения и последующим возгоранием.

Серебро – это металл, обладающий самой высокой электропроводностью. При +20 °C этот показатель равен 63,3×104 см-1. Тем не менее, производство серебряной проводки является нерентабельным, поскольку речь идет о достаточно редком металле. В большинстве случаев он идет на изготовление ювелирных изделий, украшений, монет.

Среди неблагородных цветных металлов самая высокая электропроводность характеризует медь – она составляет 57×104 см-1 при +20 °C. Помимо этого, медь хорошо справляется с постоянными электрическими нагрузками, долговечна, надежна, имеет высокую температуру плавления, поэтому может долго работать в нагретом состоянии. Все названные свойства позволяют активно применять данный металл для бытовых целей и на производстве.

Не реже меди используется алюминий, ведь по электропроводности он уступает только серебру, меди и золоту. Его температура плавления практически в два раза ниже, чем у меди, из-за чего алюминий не может выдерживать предельные нагрузки. По этой причине его применяют в сетях с невысоким напряжением. Узнать электропроводность остальных металлов можно в соответствующей таблице.

По проводимости любой сплав значительно уступает чистому металлу, что объясняется слиянием структурной сетки, вызывающим нарушение нормального функционирования электронов. Так, медные провода изготавливают только из металла с максимальной долей примесей 0,1 % или даже 0,05 %, если речь идет об отдельных разновидностях кабеля.

Приведенные показатели – это удельная электропроводность металлов, которая представляет собой отношение плотности тока к величине электрического поля в проводнике.

Опасность металлов с высокой электропроводностью

Щелочные металлы имеют крайне высокую электропроводность, объясняют этот факт тем, что в них электроны практические не привязаны к ядру и могут быть без труда выстроены в требуемой последовательности. Еще одна особенность этих металлов состоит в низкой температуре плавления в сочетании со значительной химической активностью, что обычно не позволяет использовать их в качестве материалов для кабелей.

Находясь в незащищенном виде, металлы с высокой электропроводностью несут в себе большую опасность. Прикосновение к оголенным проводам вызывает электрический ожог, разряд воздействует на внутренние органы, что нередко становится причиной мгновенной смерти человека.

Поэтому металл закрывают специальными изоляционными материалами, которые могут быть жидкими, твердыми, газообразными – конкретный тип подбирается в соответствии со сферой использования изделия. Вне зависимости от агрегатного состояния защиты она призвана изолировать электрический ток в цепи, чтобы не допустить его воздействия на окружающую среду.

Зависимость электропроводности металлов от факторов внешней среды

Проводимость не является постоянной величиной. В таблицах приведены сведения, характерные для нормальных условий или при температуре +20 °С. В реальной жизни сложно обеспечить идеальные условия для работы цепи. Удельное сопротивление, а значит, и проводимость, определяется такими характеристиками:

температурой;
давлением;
наличием магнитных полей;
светом;
агрегатным состоянием вещества.

Изменения интересующего нас параметра зависят от условий среды и свойств конкретного материала. Электропроводность ферромагнетиков, в число которых входят железо и никель, увеличивается при совпадении направления тока с направлением силовых линий магнитного поля. Зависимость электропроводности от теплопроводности металлов и окружающей температуры практически линейная, даже есть понятие температурного коэффициента сопротивления – данную величину можно уточнить в таблицах.

Правда, направление зависимости определяется конкретным веществом: у металлов оно при увеличении температуры повышается, у редкоземельных элементов и растворов электролитов увеличивается в пределах одного агрегатного состояния.

Полупроводники характеризуются гиперболической и обратной зависимостью электропроводности от температуры: рост степени нагрева приводит к повышению электропроводности металлов. Данная особенность качественно отличает проводники от полупроводников. Зависимость ρ проводников от температуры выглядит следующим образом:

На графике отображено удельное сопротивление меди, платины, железа. Некоторые металлы характеризуются иначе: ртуть при понижении температуры до 4°K становится сверхпроводимой, почти полностью теряя удельное сопротивление.

У полупроводников зависимость будет представлена так:

Когда металл переходит в жидкое агрегатное состояние, его ρ повышается, а дальнейшее изменение свойств может быть разным. Так, висмут в расплавленном виде имеет более низкое удельное сопротивление, чем при комнатной температуре, а у жидкой меди оно повышается в десять раз. Никелю свойственно выходить из линейного графика уже при достижении температуры +400 °C, но далее ρ падает.

Температурная зависимость вольфрама так высока, что приводит к перегоранию ламп накаливания: ток нагревает спираль, из-за чего ее сопротивление многократно возрастает.

Удельное сопротивление сплавов зависит от задействованной при производстве технологии. Данное свойство простой механической смеси определяется как средний показатель ее компонентов. Тогда как для сплава замещения оно окажется иным и обычно отличается в большую сторону.

Почему следует обращаться именно к нам

Мы с уважением относимся ко всем клиентам и одинаково скрупулезно выполняем задания любого объема.

Наши производственные мощности позволяют обрабатывать различные материалы:

цветные металлы;
чугун;
нержавеющую сталь.

При выполнении заказа наши специалисты применяют все известные способы механической обработки металла. Современное оборудование последнего поколения дает возможность добиваться максимального соответствия изначальным чертежам.

Для того чтобы приблизить заготовку к предъявленному заказчиком эскизу, наши специалисты используют универсальное оборудование, предназначенное для ювелирной заточки инструмента для особо сложных операций. В наших производственных цехах металл становится пластичным материалом, из которого можно выполнить любую заготовку.

Преимуществом обращения к нашим специалистам является соблюдение ими ГОСТа и всех технологических нормативов. На каждом этапе работы ведется жесткий контроль качества, поэтому мы гарантируем клиентам добросовестно выполненный продукт.

Благодаря опыту наших мастеров на выходе получается образцовое изделие, отвечающее самым взыскательным требованиям. При этом мы отталкиваемся от мощной материальной базы и ориентируемся на инновационные технологические наработки.

Мы работаем с заказчиками со всех регионов России. Если вы хотите сделать заказ на металлообработку, наши менеджеры готовы выслушать все условия. В случае необходимости клиенту предоставляется бесплатная профильная консультация.

Электрический ток в металлах: подробное объяснение

Электрический ток в металлах представляет собой упорядоченное движение свободных электронов. Более подробно об этом читайте далее в нашей статье.

Важно знать

Как известно, электрический ток – это упорядоченный поток носителей электрического заряда. Носители – это заряженные частицы, способные свободно перемещаться во всем объеме тела.

В случае металлов этими частицами являются электроны, которые высвобождаются при образовании связи между атомами металла.

Известно, что металлы в твердом состоянии имеют кристаллическую структуру. Частицы в кристаллах расположены в определенном порядке, образуя пространственную решетку (кристалл).

Наконец, кристаллическая решетка металла образована положительными ионами, погруженными в “облако” хаотически движущихся так называемых свободных электронов, также называемых электронами проводимости. В зависимости от валентности атомов металла, один атом может освободить от одного до трех электронов при образовании металлических связей. Число таких высвобожденных электронов непосредственно переводится в число носителей заряда. Это является одним из факторов, влияющих на способность металла проводить электрический ток.

Доказательством того, что ток в металлах вызывается электронами, послужили эксперименты наших отечественных физиков Леонида Исааковича Мандельштама и Николая Дмитриевича Папалекси, а также американских физиков Бальфура Стюарта и Роберта Толмана.

Способность металла проводить электрический ток может быть описана физической величиной, называемой удельным электрическим сопротивлением. Эта физическая величина обозначается греческой буквой ρ (читается как “ро”). Единицей измерения удельного сопротивления является Ом · м, т.е. произведение Ом на метр. Удельное сопротивление – это константа, которая характеризует материал и имеет различные значения для разных материалов. Например, удельное сопротивление меди составляет 1.72*10 -8 Ом · м. Это означает, что электрическое сопротивление медного проводника длиной 1 метр и площадью поперечного сечения 1 м равно 1.72*10 -8 Ом . В целом, чем ниже удельное сопротивление материала, тем лучше он проводит электрический ток.

В таблице ниже приведены некоторые примеры удельного сопротивления часто используемых металлов.

Металл	Удельное сопротивление (Ом · м)
Серебро	1.59*10 -8
Медь	1.72*10 -8
Алюминий	2.82*10 -8
Вольфрам	5.6*10 -8
Железо	10*10 -8

Удельное электрическое сопротивление может быть связано с микроскопическими свойствами материала. В частности, он зависит от концентрации носителей заряда и их подвижности.

Движение свободных электронов в металлах не является полностью “свободным”, поскольку во время их движении они взаимодействуют с другими электронами, и прежде всего с ионами кристаллической решетки. Специфика этого движения описывается так называемой классической моделью проводимости.

Основные предположения и выводы этой модели представлены в большом упрощении ниже.

Классическая модель проводимости

Без внешнего электрического поля электроны совершают тепловые хаотические движения, сталкиваясь друг с другом, а также сталкиваясь с ионами кристаллической решетки. В результате такого движения среднее положение электронов практически не меняется (см. рис. 1.).

Рис. 1. Пример траектории электрона во время его хаотического теплового движения в металле

Из-за квантовых эффектов, и в частности из-за принципа запрета Паули, который не позволяет всем электронам занимать самое низкое энергетическое состояние, средняя скорость электронов в металлах, связанная с их хаотическим тепловым движением, больше, чем скорость частиц в классическом идеальном газе той же температуры. Она составляет порядка 10 м/с.

Если электрическое напряжение U приложено к концам проводника длиной L в нем появится электрическое поле с напряженностью E = U / L

Под действием этого внешнего поля, согласно второму закону динамики, электроны ускоряются: a = F / m,

где F = e*E – сила, с которой электрическое поле действует на электрон с зарядом e. Таким образом, ускорение электрона составляет: a = e*E / m .

Ускоренное движение электрона длится лишь довольно короткое время, пока он не столкнется с ионом
кристаллической решетки. В результате такого столкновения электрон теряет практически всю свою кинетическую энергию. Однако замедленный электрон не остается в состоянии покоя – он снова ускоряется под действием электрического поля, снова сталкивается с одним из ионов из ионы кристаллической решетки и т.д. Этот эффект добавляет к скорости тепловых движений дополнительную направленную среднюю скорость u, которая из-за отрицательного заряда электрона имеет направление, противоположное напряженности внешнего электрического поля. Эта скорость называется средней скоростью дрейфа (рис. 2).

Рис. 2. Дрейф электрона под действием внешнего электрического поля

В проводнике начинает течь электрический ток с силой тока I (см. рисунок 3).

Рис. 3. Дрейфующие электроны сталкиваются с ионами кристаллической решетки

Предполагая, что движение электрона равномерно ускоряется между столкновениями с ионами решетки, с ускорением a = e*E / m , и предполагая, что в результате столкновения электрон передает всю свою кинетическую энергию кристаллической решетке, мы можем вычислить скорость, которую развивает электрон в своем свободном движении: v = a*τ . В этой формуле τ – средний интервал времени между последующими столкновениями дрейфующего электрона с ионами кристаллической решетки.

Поскольку при равномерно ускоренном движении без начальной скорости средняя скорость является средним арифметическим начальной (равной нулю) и конечной скоростью, то получаем: u = v / 2 = e*E*τ / 2*m .

Из полученной формулы следует, что скорость дрейфа, помимо внешнего электрического поля, определяется средним интервалом времени между столкновениями электронов с ионами решетки. Этот параметр зависит от многих факторов (включая температуру, кристаллическую структуру металла, дефекты кристаллической структуры, примеси) и, как выясняется, существенно влияет на электрическое сопротивление материала.

Средняя дрейфовая скорость электронов составляет порядка 10 -4 м/с. Она очень мала по сравнению со скоростью теплового движения, которая составляет порядка 10 6 м/с.

Классическая теория проводимости достаточно хорошо описывает явление электропроводности в металлах. Однако эта теория не может объяснить экспериментально наблюдаемую зависимость электрического сопротивления от температуры.

Причина упомянутой неудачи классической теории проводимости заключается в том, что она не учитывает влияние ионов решетки на движение электронов между столкновениями. Более близкие к реальности результаты дает квантовая теория проводимости, которая описывает электроны как частицы, подверженные квантовой статистике, движущиеся в периодическом электрическом поле, создаваемом положительными ионами решетки.

Выводы простым языком

Отрицательный заряд всех свободных электронов по абсолютному значению равен положительному заряду всех ионов решётки. Поэтому в обычных условиях металл электрически нейтрален. Свободные электроны в нём движутся беспорядочно. Но если в металле создать электрическое поле, то свободные электроны начнут двигаться направленно под действием электрических сил. Возникнет электрический ток. Беспорядочное движение электронов при этом сохраняется, подобно тому как сохраняется беспорядочное движение в стайке мошкары, когда под действием ветра она перемещается в одном направлении.

« Скорость движения самих электронов в проводнике под действием электрического поля невелика – несколько миллиметров в секунду, а иногда и ещё меньше. Но как только в проводнике возникает электрическое поле, оно с огромной скоростью, близкой к скорости света в вакууме (300 000 км/c), распространяетcя по всей длине проводника. »
Перышкин А. В. Физика 8. – М.: Дрофа, 2010

Как пример, электрический сигнал, посланный, например, по проводам из Москвы во Владивосток (s = 8000 км), приходит туда примерно через 0,03 с.

Одновременно с распространением электрического поля все электроны начинают двигаться в одном направлении по всей длине проводника. Так, например, когда цепь электрической лампы замкнута, электроны в спирали лампы также движутся упорядоченно.

Сравнение электрического тока с потоком воды в водопроводной системе и распространения электрического поля с распространением давления воды поможет нам понять это. Когда вода поднимается в резервуар для воды, давление (напор) воды очень быстро распространяется по всей системе водоснабжения. Когда мы включаем кран, вода уже находится под давлением и сразу же начинает течь. Но вода, которая была в кране, течет, а вода из башни достигает крана гораздо позже, потому что вода движется с меньшей скоростью, чем распространяется давление.

Когда говорят о скорости распространения электрического тока в проводнике, то имеют в виду скорость распространения по проводнику электрического поля.

Электропроводность: объяснение, формулы, единица измерения, таблица

Почему медь проводит электричество лучше, чем вода? Прочитав эту статью, вы больше не будете задавать себе больше этот вопрос. Далее мы обсудим электропроводность и рассмотрим формулы, которые описывают это понятие. Наконец, вы можете проверить свои знания на двух примерах.

Простое объяснение.

Электропроводность – это физическая величина, которая описывает насколько хорошо определенный материал проводит электричество.

Формулы

Существует три различных формульных обозначения удельной электропроводности σ (греч. сигма), k (каппа) и γ (гамма). В дальнейшем мы будем использовать σ. Формула электропроводности, также называемой удельной электропроводностью, описывается формулой:

σ = 1 / ρ .

Здесь ρ называется удельным сопротивлением. Вы можете рассчитать электрическое сопротивление R проводника с учетом его параметров следующим образом: R = ( ρ * l ) / S .

Таким образом, сопротивление R равно удельному сопротивлению ρ , умноженному на длину проводника l, деленному на площадь поперечного сечения S. Если теперь вы хотите выразить эту формулу через удельную электропроводность σ = 1 / ρ , полезно знать, что электрическая проводимость G проводника выражается следующим образом: G = 1 / R .

Если в верхнюю формулу подставить удельную электропроводность σ и электрическую проводимость G, то получится следующее: 1 / G = ( 1 / σ ) * ( l / S ) .

Путем дальнейшего преобразования можно получить выражение: G = σ * S / l .

С помощью электропроводности можно также описать важную зависимость между плотностью электрического тока и напряженностью электрического поля с помощью выражения: J = σ * E .

Единица измерения

Единицей удельной электропроводности σ в СИ является: [ σ ] = 1 См/м ( Сименс на метр ).

Эти единицы определяются по формуле G = σ * S / l . Если решить эту формулу в соответствии с σ, то получим σ = G * l / S .

Единица измерения электрической проводимости G задается как: [ G ] = 1 / σ = 1 См ( Сименс, международное обозначение: S ).

Если теперь ввести в формулу все единицы измерения, то получится:

[ σ ] = 1 См * 1 м / м 2 = 1 См / м .

Вы также будете чаще использовать единицы измерения См / см , м / Ом * мм 2 или См * м / мм 2 . Вы можете преобразовать отдельные измеряемые переменные так: См / см = См / 10 -2 м и так: м / Ом * мм 2 = См * м / мм 2 = См * м / 10 -3 м * 10 -3 м = 10 6 См / м .

В зависимости от количества свободно перемещающихся электронов один материал проводит лучше, чем другой. В принципе, любой материал является проводящим, но в изоляторах, например, протекающий электрический ток ничтожно мал, поэтому здесь мы говорим о непроводниках.

В металлических связях валентные электроны, т.е. крайние электроны в атоме, свободно подвижны. Они расположены в так называемой полосе проводимости. Находящиеся там электроны образуют так называемый электронный газ. Соответственно, металлы являются сравнительно хорошими проводниками. Если теперь подать электрическое напряжение на металл, валентные электроны медленно движутся к положительному полюсу, потому что он их притягивает.

Рис. 1. Движение электронов в металле

На рисунке 1 видно, что некоторые электроны не могут быть притянуты непосредственно к положительному полюсу, потому что на пути стоит, так сказать, твердое атомное ядро. Там они замедляются и в некоторой степени отклоняются. Именно поэтому электроны не могут ускоряться в металле бесконечно, и именно так возникает удельное сопротивление или электропроводность.

Теперь вы также можете измерить удельную электропроводность в металле с помощью следующей формулы: σ = ( n * e 2 * τ ) / m .

В этой формуле n означает число электронов, e – заряд электрона, m – массу электрона, а τ – среднее время полета электрона между двумя столкновениями.

Таблица удельной электропроводности

Для большинства веществ уже известны значения удельной электропроводности. Некоторые из них вы можете найти в следующей таблице ниже. Все значения в этой таблице действительны для комнатной температуры, т.е. 25°C.

Вещество	Удельная электропроводность в См / м
Серебро	62 · 10 6
Медь	58 · 10 6
Золото	45,2 · 10 6
Алюминий	37,7 · 10 6
Вольфрам	19 · 10 6
Латунь	15,5 · 10 6
Железо	9,93 · 10 6
Нержавеющая сталь (WNr. 1,4301)	1,36 · 10 6
Германий (легирование	2
Кремний (легирование	0,5 · 10 -3
Морская вода	примерно 5
Водопроводная вода	примерно 0,05
Дистиллированная вода	5 · 10 -6
Изолятор	обычно

Таблица удельной электропроводности некоторых веществ при температуре 25 °C

Удельная электропроводность сильно зависит от температуры, поэтому указанные значения применимы только при 25°C. При повышении температуры вибрация решетки в веществе становится выше. Это нарушает поток электронов, и поэтому электропроводность уменьшается с ростом температуры.

Из таблицы видно, что медь имеет вторую по величине электропроводность, поэтому медные кабели очень часто используются в электротехнике. Серебро обладает еще более высокой проводимостью, но стоит намного дороже меди.

Интересно также сравнение между морской и дистиллированной водой. Здесь электропроводность возникает благодаря растворенным в воде ионам. Морская вода имеет очень высокую долю соли, которая растворяется в воде. Эти ионы передают электрический ток. В дистиллированной воде нет растворенных ионов, поэтому в ней практически не может протекать электрический ток. Поэтому электропроводность морской воды намного выше, чем дистиллированной.

Примеры задач

Для более детального рассмотрения приведём два примера расчетов.

В первой задаче представьте, что у вас есть провод длиной 2 м с поперечным сечением 0,5 мм 2 . Электрическое сопротивление провода при комнатной температуре составляет 106 мОм. Из какого материала изготовлен провод?

Решение данной задачи можно найти с помощью формулы: R = ( 1 / σ ) * ( l / S ). Из этой формулы найдём σ = l / ( S * R ) .

Теперь вы можете вставить заданные значения, убедившись, что вы перевели сечение в м 2 .

σ = l / ( S * R ) = 2 м / ( ( 0,5 * 10 -6 м 2 ) * ( 1 / 106 * 10 -3 Ом ) ) = 37, 7 * 10 6 См / м .

Наконец, вы ищите в таблице, какой материал имеет удельную электропроводность σ = 37, 7 * 10 6 См / м и приходите к выводу, что провод сделан из алюминия.

В задаче 2 вам дано только удельное сопротивление образца с 735 * 10 -9 Ом * м. Из какого материла изготовлен образец?

Вы можете использовать формулу σ = 1 / ρ для расчёта удельной электропроводности. После подстановки значений в эту формулу вы получите: σ = 1 / ρ = 1 / 735 * 10 -9 Ом * м = 1,36 * 10 6 См / м .

Если вы снова заглянете в таблицу, то обнаружите, что образец должен быть изготовлен из нержавеющей стали.

VIII Международная студенческая научная конференция Студенческий научный форум - 2016

Электропроводность – это свойство тела или вещества проводить ток, а также физическая величина, численно характеризующая эту способность. Электропроводность зависит от количества свободных ионов, содержащихся в проводнике, движение которых является электрическим током. В системе СИ электропроводность обозначается как S и измеряется в сименсах.

В зависимости от величины электропроводности вещества можно условно разделить на три группы: проводники, диэлектрики и полупроводники. Однако, провести четкие границы между группами невозможно.

Проводники имеют большое количество свободных ионов, а следственно и большую электропроводность. Они делятся на два рода, которые отличаются друг от друга физической природой протекания электрического тока. К первому роду относятся металлы с электронной проводимостью, то есть прохождение тока по ним обусловлено движением свободных электронов. К проводникам второго рода относятся растворы кислот, щелочей и солей, которые называют электролитами. Прохождение тока по электролитам обусловлено движением положительных и отрицательных ионов. Такие проводники имеют ионную проводимость. Электропроводность проводников больше 10 6 (ом·м) -1 . [3]

Диэлектрики имеют наоборот маленькое количество свободных ионов, что означает малую электропроводность и практически неспособность проводить электрический ток. К ним можно отнести дерево, смолы, пластмассы, стекло и т.п. Электропроводность диэлектриков меньше 10 6 (ом·м) -1 . [3]

Полупроводники имеют проводящие свойства средние между проводниками и диэлектриками. К полупроводникам относятся, например, германий, кремний, селен и другие искусственные соединения. [3]

На электропроводность вещества или тела влияет температура вещества. Однако, зависимость от температуры различная у разных веществ. У металлов данная зависимость определяется уменьшением времени свободного пробега электронов с ростом температуры. При увеличении температуры происходит возрастание тепловых колебаний кристаллической решетки, на которой рассеиваются электроны и соответственно электропроводность уменьшается. Для полупроводников зависимость иная. При повышении температуры электропроводность увеличивается, так как увеличивается число электронов проводимости и положительных носителей заряда. Диэлектрики также имеют увеличенную электропроводность, но при очень высоком электрическом напряжении. [2]

Металлы имеют свойство проводить ток. Это обусловлено тем, что электромагнитное поле воздействует на проводниковый металл, в следствие чего электрон ускоряется настолько, что теряет связь с атомом.

Электронная теория проводимости металлов создана П. Друде в 1900 г., которая далее получила развитие в работах Г. Лоренца. С точки зрения данной теории высокая электропроводность металлов обусловлена наличием очень большого числа носителей заряда – электронов проводимости, перемещающихся по всему объему проводника. При своем движении электроны проводимости сталкиваются с ионами кристаллической решетки металла. Следуя из этого средняя длина свободного пробега электронов равна 10 -8 см. [1]

Плотность тока, проходящая через проводник будет равна общему заряду всех электронов, проходящих за одну секунду через единицу площади поперечного сечения проводника.

Читайте также: