Изгибаемые элементы металлических конструкций
Элементы металлических конструкций в процессе эксплуатации подвергаются действию растяжения, сжатия, изгиба, кручении и различных комбинаций этих воздействий. Рассмотрим методы расчета на прочность элементов металлических конструкций т.е. методы расчета по первому предельному состоянию.
Центрально-сжатые и центрально - растянутые элементы. Ранее для вычисления напряжений в этом случае была выведена формула ( 3.1 ). Эту формулу легко превратить в соотношение для проверки прочности.
где Аn - площадь поперечного сечения элемента за вычетом ослаблений; N - усилие от действия расчетных нагрузок; γc - коэффициент условий работы; R - расчетное сопротивление. Если расчет ведется по упругой стадии, R = Ry. Если расчет ведется для условий, когда возможна эксплуатация конструкции и после достижения материалом напряжений текучести, в качестве расчетного сопротивления выбирается максимальное значение из величин Ry и Ru / γu . Здесь Ry и R u - расчетные сопротивления материала, соотвественно, по пределу текучести и по временному сопротивлению;
γu = 1,3 - коэффициент надежности по материалу при расчете конструкций по временному сопротивлению.
Относительно разницы между растяжением и сжатием. Формула (4.1) для растяжения абсолютно корректна. Что же касается сжатия, то это соотношение справедливо только для коротких стержней. Известно, что стержни при сжатии, до исчерпания прочности самого сечения, могут потерять устойчивость, см. рис.4.1. Следует заметить, что хотя это напряженное состояние называется «центральным сжатием» на практике оно никогда не реализуется. Происходит это по многим причинам. Во-первых, нагрузка никогда не может быть приложена точно в центре сечения, так как все конструктивные элементы выполняются с допусками. Во-вторых, материал в сечении и по длине стержня всегда неоднороден. Эти и другие причины приводят к тому, что сжимающая сила оказывается всегда приложенной с некоторым эксцентриситетом к центру тяжести поперечного сечения и этот эксцентриситет создает дополнительный изгибающий момент, приводящий в итоге к потере устойчивости.
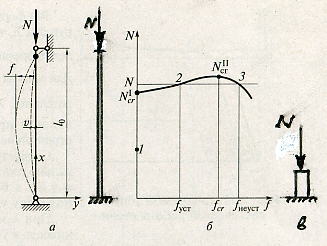
Рис. 4.1. Работа центрально сжатого стержня:
а - стержень и его расчетная схема, б – зависимость между нагрузкой и прогибом стержня,
в - сжатие короткого стержня.
Такое напряженное состояние стержня при действии сжимающей силы называется продольным изгибом. Поэтому формула проверки прочности стержня при сжатии будет
выглядеть так: σ = N / ( φ A ) ≤ Ry γc , ( 4.2 )
где: φ - коэффициент продольного изгиба; A – площадь поперечного сечения стержня. Коэффициент φ всегда меньше 1 и зависит от гибкости стержня λ. Гибкость стержня зависит от способа его закрепления по концам и от геометрических характеристик сечения: λ =где - расчетная длина стержня; μ - коэффициент расчетной длины;
i =При действии изгиба производится проверка по нормальным и касательным напряжениям. При расчете по упругой стадии проверка нормальных напряжений производится по соотношению преобразованному из соотношения ( 3.2 ):
где M - расчетный изгибающий момент; Wn,min - момент сопротивления сечения
с учетом ослаблений; σmax - напряжение в крайних волокнах поперечного сечения.
Касательные напряжения проверяются на основании формулы Н.Г. Журавского:
τ = Q S / ( J t ) ≤ Rs γc , ( 4.5 )
где Q - поперечная сила от действия расчетных нагрузок; S - статический момент сдвигаемой части сечения относительно нейтральной оси; J - момент инерции сечения относительно нейтральной оси; t - толщина стенки в плоскости сдвига; Rs - расчетное сопротивление металла сдвигу.
При действии изгибающих моментов в двух плоскостях ( случай косого изгиба) проверка нормальных напряжений выполняется по соотношению:
где Mx , My, Wnx, Wny - изгибающие моменты и моменты сопротивления сечения относительно осей изгиба X и Y.
По мере роста нагрузки в сечении изгибаемого элемента могут развиваться пластические деформации. Развитие пластических деформаций в сечении изгибаемого элемента иллюстрируется эпюрами на рис. 4.2.
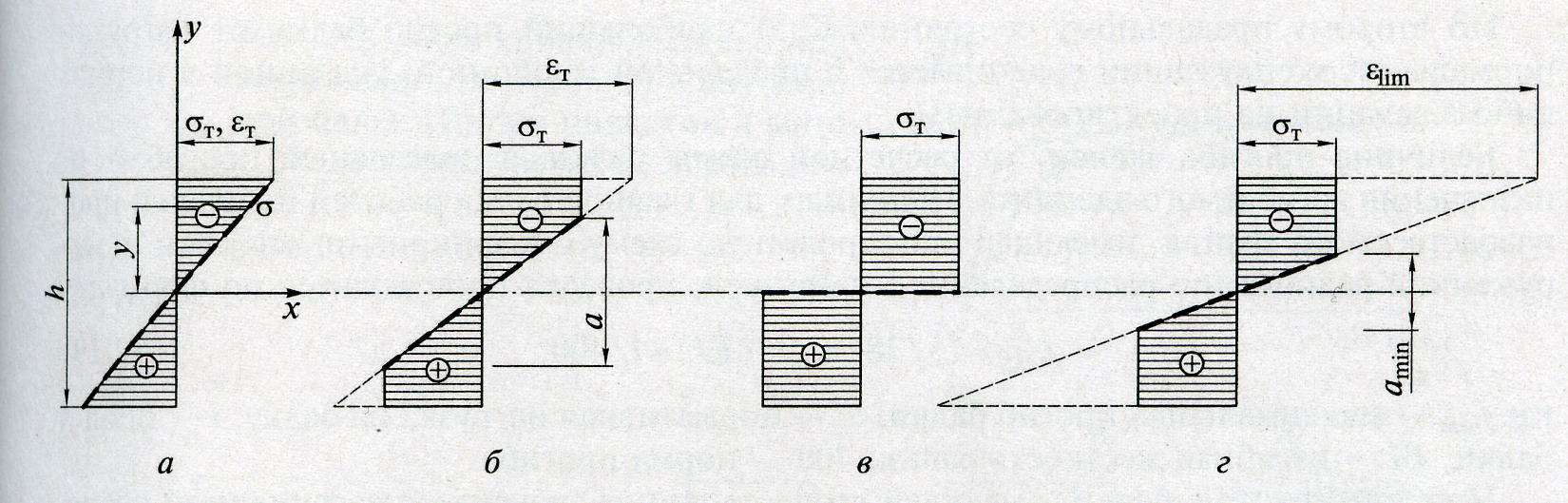
Рис.4.2. Изменение эпюры напряжений в изгибаемом элементе при развитии
пластических деформацйий в материале
а – в упругой стадии, б – в упруго-пластической, в – шарнир пластичности, г – при ограниченной пластичности
При проверке прочности с учетом пластических деформаций, формула получается из соотношения ( 4.4 ) заменой величины Wn на величину Wn,пл = C Wn .
где коэффициент c учитывает увеличение момента сопротивления и определяется по нормам. Кроме того это соотношение разрешается применять только для случаев
когда τ ≤ 0,9 Rs . А проверка прочности на сдвиг в этом случае производится только в опорных сечениях разрезных балок, там где изгибающие моменты равны нулю. Для тавровых балок проверка производится при τ ≤ 0,5 Rs по соотношению
где t - толщина стенки; h - высота балки.
Для случая косого изгиба при τ ≤ 0,5 Rs проверка производится по соотношению:
где Сx и Сy коэффициенты зависящие от формы сечения; β - коэффициент меньший единицы и зависит от величины касательного напряжения τ. При работе элементов металлических конструкций возможны случаи сложного напряженного состояния когда совместно действуют изгиб и усилия растяжения или сжатия. В общем случае, когда действует осевая сила N и моменты в двух направлениях Mx и My предельную несущую способность проверяют по формуле:
где An , Wnx , Wny - площадь и соответстующие моменты сопротивления нетто поперечного сечения стержня; Сx и Сy - коэффициенты, учитывающие увеличение несущей способности материала при развитии пластических деформаций; n - показатель степени. Три последние величины принимаются в соответстии с действующими нормами. Для конструкций работающих в упругой стадии и в случаях когда развитие пластических деформаций недопустимо, в проверочной формуле следует положить n = Сx = Сy= 1 и соотношение ( 4.10 a ) перейдет в соотношение для проверки по упругой стадии работы материала при действии нормальной силы и изгиба в двух плоскостях:
В случае действия сжимающей силы и изгиба в двух направлениях может также произойти потеря устойчивости и при этом необходимо произвести соответствующие проверки. Потеря устойчивости может произойти как в плоскости действия момента, так и из плоскости, это зависит от соотношения гибкостей стержня в этих плоскостях. Формула проверки устойчивости в этом случае аналогична формуле проверки для случая продольного изгиба: N / ( φe A ) ≤ Ry γc , ( 4.11 )
Однако коэффициент потери устойчивости φe зависит в данном соотношении от приведенной гибкости ef . Способ вычисления этих величин приведен в нормах. Проверка на устойчивость из плоскости действия момента производится по формуле:
Расчет изгибаемых элементов металлических конструкций
В изгибаемых эл-тах возникает неск-ко видов напр-ия. Все случаи работы д.б. рассчитаны по предел сост-ям. Для 1-ой группы – вязкое или усталостное разрушение, потеря устой-ти, текучесть мат-ла. Для 2-ой группы – достижение предельных перемещ-й.
σ – норм напр-ия, образуются от действия изгиб м-та; τ – касат напр-ия, образуются от действия попер сил; σlok – мест напр-ия, образуются в месте приложения крупной сосредоточ силы или опорной р-ии.
Кроме того при расчете д.б. учтено совместное действие норм и касат напр-ий, под действием к-ых возникает сложное напряжен сост-ие, несущее в себе новые кач-ва.
1.Расчет по норм напр-ям. Расчет на проч-ть изгибаемых эл-тов, раб-щих в пределах упругих деф-ций, при изгибе в одной из гл пл-стей вып-ют по формуле: , - изгиб м-т, определенный по расч нагрузкам; - м-т сопр-ния ослабленного сечения, определенный по упругой стадии работы эл-та. Расчет на проч-ть эл-тов с учетом развития пластич деф-ций, изгибаемых в одной из гл пл-стей, вып-ют по формуле: , - коэф,учит-ющий пластич работу стали, опред-ся: п. 5.18 СНиП. Учет пластич работы стали разреш-ся для изд-ий из стали с пределом текучести , при соблюдении усл-ий надежного обеспечения общей и мест устой-ти кон-ций и возд-вии т-ко статич нагрузок.
2.Расчет по касат напр-ям. Наиб. касат напр-ия приход-ся на нейтрал ось, на уровне к-ой и проверяют стенку балки при расчете. Знач-я касат напр-ий в сеч-ях изгибаемых эл-тов д. удовлетворять усл-ию: , - попер сила от расч нагрузок; - статич м-т брутто сдвигающейся части сеч-я, относит-но нейтрал оси; - м-т инерции сеч-я относит-но нейтрал оси; - δ стенки балки.
3.Расчет по мест напр-ям. Мест сж-щие напр-я, возник-щие в местах прилож-я сосредоточ силы резко снижают мест устой-ть стенки. Поэтому в таких местах реком-ся устан-ть ребра жесткости. Если избавиться от местн напр-ий невозм-но, то необх-ма проверка по ф-ле: , - расч знач-е нагрузки; - условная длина распределения нагрузки, определенная из усл-й опирания. (Рис.), , - ширина прилож-я нагрузки; - δверхнего пояса балки.
4.При сложном напряженном сост-ии от совместного действия норм и касат напр-ний. Для стенок балок, раб-щих в пределах упругих деф-ций д. вып-ся усл-я: , - норм напр-ия ср пл-ти стенки, //-ные оси балки; - норм- напр-ия ср пл-ти стенки, ┴-ные оси балки, в т.ч. ; - касат напр-ия в той же точке балки, для к-ых определ-ся норм напр-ия.
5.Проверка общей устой-ти. При располож-и нагрузки в пл-ти гл оси инерции, изгибаемый эл-т при потере устой-ти сначала изгиб-ся в своей пл-ти, а затем при достиж-и нагрузкой критич знач-я начинает закручиваться и выходить из пл-ти изгиба. Расчет на устой-сть балок двутаврового сеч-я, изгибаемых в пл-сти стенки и удовлетворяющих рассм-ным ранее усл-ям, вып-ют по ф-ле: , - м-т сопр-ния для сжатого пояса; - коэф., снижения расч сопр-ний при изгибно-крутильной форме потери устой-ти балок, определяемый в соотв-и с прил. 7 СНиП. Проверка общей устой-ти балок не произ-ся, если: 1.Нагрузка передается ч/з сплошной жесткий настил, приваренный к верхнему поясу балки. 2.Отн-ие расч длины балки кширине сжатого пояса не превышает знач-й, определяемых по ф-лам табл. 8 СНиП для балок двутаврового (симметричного) сеч-я и для балок с развитым сжатым поясом при усл-ии, что
6.Потеря мест устой-ти. Прокатные профили запроект-ны так рац-но, что для них невозм-на потеря мест устой-ти. Поэтому такая проверка не произ-ся. Составные эл-ты обязат-но проверяются на мест устой-ть. (Рис) Устой-ть стенок балок не треб-ся проверять, если условная гибкость стенки удовлетворяет усл-ям: , - при отсутствии местного напр-ия в балках с двусторонними поясными швами; - при отсутствии мест напр-ия в балках с односторонними поясными швами; - при наличии мест напр-ия в балках с двусторонними поясными швами. При этом следует устан-ть попер осн ребра жесткости в соотв-вии с п. 7.10; 7.12 и 7.13 СНиП. Расчет на устой-ть стенок балок симметрич сечения, укрепленных т-ко попереч осн ребрами жесткости при наличии мест напр-ия, опред-ют по ф-ле: , - норм критич напр-ие. Устой-ть полки балки проверяют по отн-нию: , - опред-ся по ф-лам табл.30 СНиП.
7.Проверка упругих деф-ций. При работе соор-ий в балках м. появиться деф-ции, затрудняющие экспл-цию кон-ции. Деф-ции проверяют на упругой стадии работы кон-ции от возд-вия норм нагрузок, при этом возник-щий прогиб не д. превышать предельно допустимый. (Рис.) . Относит прогиб: . Величина предельно допустимого прогиба эл-тов дана в СНиП «Нагрузки и воздействия».
Расчет элементов металлических конструкций на изгиб
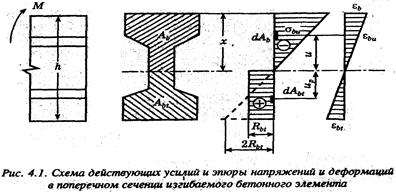
Бетонные изгибаемые элементы рассчитывают из условия равновесия в предельном состоянии. Перед образованием трещин на растянутой грани напряжения достигают величины Rbt а эпюра в растянутой зоне вследствие развития значительных пластических деформаций сильно искривляется, что позволяет без большой погрешности заменить ее прямоугольной. Нормальные напряжения на сжатой грани существенно меньше предельных, поэтому эпюра напряжений в сжатой зоне может быть принята треугольной. Ее наклон принимают таким, чтобы при продолжении в растянутой зоне она отсекала на крайнем волокне отрезок, равный 2 Rbt(рис. 4.1). Это условие равносильно принятию модуля
деформации крайнего растянутого волокна бетона равным половине модуля упругости при сжатии (Е'bt= 0,5ЕЬ).
Таким образом, за расчетную эпюру внутренних напряжений в бетонном сечении вместо фактической криволинейной принята треугольная в сжатой зоне и прямоугольная в растянутой. Принимается справедливой также гипотеза плоских сечений.
где Wpl — момент сопротивления для растянутой грани сечения, определяемый с учетом неупругих свойств бетона.
Для определения Wpl следует сначала найти положение нейтральной оси, соответствующее принятой эпюре напряжений. Для этого составляют уравнение проекций всех сил на продольную ось элемента, из которого получают статический момент сжатой
где А bt— площадь растянутой зоны сечения.
В общем случае положение нейтральной оси, т.е. величину х, определяют последовательным приближением. Однако для большинства встречающихся на практике видов сечений, а именно, когда нейтральная ось заведомо пересекает участок сечения с постоянной шириной (прямоугольное, тавровое, коробчатое и др.), выражение (4.2) легко преобразуют в уравнение с одним неизвестным, из которого можно непосредственно определить х.
Выражение упругопластического момента сопротивления сечения получим из уравнения моментов всех сил относительно нейтральной оси, из которого
гдеlc — момент инерции сжатой зоны сечения относительно нулевой линии; S, — статический момент растянутой части сечения относительно той же оси.
Величину Wpl допускается определять также по формуле
т.е. умножениенм величины упругого момента сопротивления крайнего растянутого волокна сечения относительно оси, проходящий через центр тяжести сечения Wel, на коэффициент у, значения которого для сечения различной формы приводятся в пособиях по проектированию конструкций [10]*. Например, для прямоугольного и таврового сечения с полкой в сжатой зоне у = 1,75. Это свидетельствует о том, что учет неупругих деформаций в растянутой зоне существенно увеличивает расчетную прочность бетонных элементов, что хорошо согласуется с данными опытов. Элементы прямоугольной формы сечения допускается рассчитывать по формуле
Основы работы и расчета изгибаемых элементов

Рис.2.1 Изменение эпюры напряжений в изгибаемом элементе при развитии пластических деформаций в материале: а — в упругой стадии; б — в упруго-пластической; в — шарнир пластичности; г — при ограниченной пластичности
Для изгибаемых стержней (балок), у которых пролет значительно превышает высоту поперечного сечения (в 5 и более раз), экспериментально подтверждается гипотеза плоских сечений Бернулли. В соответствии с этой гипотезой изменение деформаций по высоте сечения происходит по линейному закону, напряжения распределяются аналогично только до предела текучести sт.
Для проверки прочности изгибаемых элементов, работающих в пределах упругих деформаций, в соответствии с основным неравенством первого предельного состояния (2.4) необходимо, чтобы максимальные нормальные и касательные напряжения в балке от расчетной нагрузки не превосходили соответствующих расчетных сопротивлений:
где M и Q — максимальные момент и поперечная сила в балке от расчетной нагрузки;
Wn — момент сопротивления нетто поперечного сечения балки, в случае несимметричного сечения балки выбирается Wnmin = Ix / ymax ;
S — статический момент сдвигающейся части сечения относительно нейтральной оси;
I — момент инерции сечения балки;
t — толщина стенки.
По второму предельному состоянию наибольший прогиб балки от нагрузки нормальной эксплуатации сравнивается с предельной величиной, указанной в нормах либо в задании на проектирование.
Легко показать, что в пределах площадки текучести, когда фибровые деформации балки не превышают 2 %, площадь эпюры на рис.2.1, б отличается от предельной (рис.2.1, в) всего на 0,2 % для прямоугольных сечений и на 0,1 % для двутавров. Поэтому с небольшой погрешностью, но значительным упрощением для дальнейшего анализа можно использовать предельную эпюру по рис.2.1, в.
Однако имеется еще одно противоречие, давшее название этому предельному случаю. Бесконечным деформациям должна соответствовать бесконечная кривизна. Для идеально пластичных материалов это может произойти, когда взаимный угол поворота частей балок, разделенных рассматриваемым сечением, будет стремиться к бесконечности. Кинематически это соответствует шарнирному механизму, подвижность которого обеспечивается пластическими свойствами материала. Отсюда появилось название пластический шарнир, определяющее предельную несущую способность изгибаемого элемента.
В отличие от механического пластический шарнир исчезает, как только изгибающий момент меняет направление, так как материал при этом восстанавливает упругие свойства.
Предельный момент в шарнире пластичности для балки произвольного сечения определяется исходя из эпюры, представленной на рис. 2.1, в:
где S в и S н — статические моменты верхней и нижней частей сечения относительно нейтральной оси при пластическом шарнире;
dA — элемент площади поперечного сечения балки.
В формуле введено обозначение W пл = | S в | + | S н |, называемое пластическим моментом сопротивления.
характеризующий резерв несущей способности изгибаемого элемента, обусловленный пластической работой материала.

Подставляя эти выражения в предыдущую формулу, получаем
где Af / Aw — отношение площадей поперечного сечения пояса и стенки.

Рис. 2.2. Зависимость коэффициента с от формы поперечного сечения изгибаемого элемента: а — для ромбического сечения; б — для прямоугольного; в — для двутаврового; г — для фермы
Для прокатных двутавров различных типов в среднем Af/Aw ~ 0,67, чему соответствует значение с = 1,1.
Устремляя площадь поясов к нулю, из двутаврового (см. рис. 2.2, в) получаем прямоугольное сечение (рис. 2.2, б), а из формулы при Afà0 с = 1,5, т.е. при использовании пластических деформаций несущая способность балки прямоугольного сечения возрастает в 1,5 раза.
Устремляя площадь стенки к нулю, как и в предыдущем случае, из двутавра получаем расчетное сечение фермы либо балки с гибкой стенкой (рис. 2.2, г), в которых изгибающий момент воспринимается практически только поясами. Из формулы при Awà 0 получаем с = 1.
Действительно, пояса фермы при шарнирном сопряжении элементов в узлах работают на осевое растяжение (сжатие). Появление в поясах пластических деформаций приводит к исчерпанию несущей способности изгибаемого элемента (фермы). Для таких сечений пластического резерва нет.
Очевидно, наибольшим пластическим резервом будет обладать балка с поперечным сечением, показанным на рис. 2.2, а, для нее с = 2. Однако это сечение при прочих равных условиях (пролет, нагрузка, расчетное сопротивление материала и пр.) является наименее экономичным по расходу материала из всех, показанных на рис. 2.2. Наименее металлоемким будет сечение, показанное на рис. 2.2, г.
Формула для проверки прочности изгибаемых элементов при наличии пластических деформаций (пластический шарнир)
При рассмотренном многокомпонентном напряженном состоянии проверку прочности балки можно производить по следующей формуле:
где 1,15 — коэффициент, учитывающий развитие пластических деформаций в балке.
При изгибе относительно двух главных осей инерции поперечного сечения балки (х, у) — косом изгибе — проверку прочности с учетом пластических деформаций допускается осуществлять по упрощенной формуле
где сх и су даются в зависимости от формы сечения b зависит от величины txy.
Основы работы и расчета на устойчивость центрально сжатых стержней
Исчерпание несущей способности длинных гибких стержней, работающих на осевое сжатие, происходит от потери устойчивости.
При фиксированном N = const, давая стержню возможное перемещение, можно подсчитать приращение работ внешних d Ае и внутренних d А i сил. Если d Ai > d Ae то состояние стержня будет устойчивым, при d Ai > d Ae — неустойчивым, при d Ai = d Ae — критическим.
В первом случае разница между виртуальными работами возвращает систему в первоначальное состояние. Во втором случае приращения работы внутренних сил d Ai недостаточно, чтобы вернуть систему в первоначальное состояние, стержень теряет устойчивость. Третий случай является пограничным, критическим.
При изучении проблемы устойчивости стержней приращения работ на возможных перемещениях можно заменить приращениями соответствующих моментов d Ме и dМi вследствие их прямой пропорциональной зависимости.
Для идеально упругого и прямолинейного стержня при фиксированном N = const приращение момента внешних сил при возможном прогибе с амплитудой n равно d Ме = N n . Приращение момента внутренних сил d М i = ρEI, где El — жесткость стержня; ρ = -у" - кривизна.

Рис. 2.3 Работа центрально сжатого стержня:
а — расчетная схема; б — зависимость между нагрузкой и прогибом стержня
Соответствующее критическое напряжение будет иметь вид
где А — площадь поперечного сечения стержня;l = l 0 / i — гибкость стержня;
l0 = m l — расчетная длина стержня;
m — коэффициент приведения, зависящий от способа закрепления концов стержня.
Эта формула справедлива при постоянном модуле упругости Е, т.е. при напряжениях, не превышающих предел пропорциональности scr < sпц, при этом l> p пц = 20 кН/см 2 , следовательно, l > 100. Для сталей повышенной прочности применимость формулы Эйлера ограничена значением l>85. Следует заметить, что на практике гибкости центрально сжатых стержней (колонн, элементов ферм, рам и т.п.) в большинстве случаев составляют примерно половину указанных предельных.
При lменьше предельных стержни теряют устойчивость в упругопластической стадии работы материала с касательным модулем деформации Е t = d s/ d e < Е.
Местная устойчивость элементов металлических конструкций
Вследствие высокой прочности металла требуемая площадь поперечного сечения конструкции мала. Для более эффективного использования высокопрочного материала в сжатых стержнях необходимо увеличивать габаритные размеры поперечного сечения, что приводит к уменьшению толщин элементов, составляющих стержень (стенки, пояса). При этом возникает опасность потери местной устойчивости тонкостенных элементов раньше, чем конструкция потеряет несущую способность от исчерпания прочности материала, либо потери общей устойчивости (рис.).
Потеря местной устойчивости сопровождается выпучиванием тонких пластин, вследствие чего они частично или полностью выключаются из работы на сжатие. Сечение ослабляется, изменяется форма его рабочей части, смещаются центр тяжести и центр изгиба. Это приводит к возникновению дополнительного изгиба и к закручиванию. В результате стержень теряет общую устойчивость.
В соответствии с напряженным состоянием конструкции составляющие ее элементы (тонкие пластины) могут терять устойчивость от нормальных напряжений (пояса и стенка колонн и балок), от касательных напряжений (опорная панель стенки балки) и от совместного действия тех и других.

Для повышения сопротивления пластин выпучиванию необходимо либо увеличивать их толщину, либо подкреплять ребрами жесткости, поставленными перпендикулярно плоскости пластины.
В последнем случае тонкая пластина расчленяется ребрами на мелкие отсеки, обладающие большей устойчивостью.
При решении задач местной устойчивости полагают, что отдельные элементы, составляющие стержень, работают как пластинки, соединенные между собой шарнирными, жесткими либо упругоподатливыми связями в зависимости от конкретных условий.
Критическое состояние таких пластин характеризуется равенством вариаций работ внутренних и внешних сил на возможном перемещении d А i = d Ае.
Рис. 2.5 Потеря местной устойчивости тонкостенных элементов:
а — балки; 6 — колонны
Пояс двутавровой балки
Расчетная схема представляет собой длинную пластину толщиной t = tf и шириной, равной свесу пояса b = bef, имеющую шарнирное закрепление по одной длинной стороне; противоположная сторона свободна.
В реальных сварных балках пояса всегда имеют некоторую случайную кривизну (грибовидность от сварки поясными швами), что приводит к фактическому уменьшению критической силы. Пояс, будучи соединенным со стенкой, обеспечивает некоторое упругое защемление стенки в том случае, если они будут терять местную устойчивость одновременно.
С учетом этих факторов в нормах принято значение l ’uf=0,5, которому соответствует к = 0,278, где k = 0,456+(bef) 2 /(a) 2 . При проверке прочности балки может оказаться, что фактические напряжения в ней будут меньше расчетного сопротивления s = M/W< Ry, что дает дополнительный резерв устойчивости пояса. Отсюда имеем окончательно
Отсюда видно, что с точки зрения обеспечения местной устойчивости тонкостенных элементов конструкций применение сталей повышенной прочности невыгодно.
Если балка работает в упругопластической стадии, пояса ее находятся, как правило, в пластическом состоянии. В этом случае предельная гибкость пояса снижается до l uf =0,3. При нормировании местной устойчивости пояса балки, работающей в упругопластической стадии, исходят из принципа равноустойчивости пояса и стенки балки.
Расчет элементов металлических конструкций при воздействии переменных нагрузок (проверка на усталость)
При действии переменных многократно повторяющихся нагрузок разрушение конструкции может произойти от усталости металла при напряжениях значительно ниже предела текучести.
Разрушение происходит без заметных пластических деформаций, имеет хрупкий характер. Это наблюдается в таких конструкциях, как подкрановые балки, балки рабочих площадок при загружении их подвижным составом, элементы бункерных эстакад, конструкции, испытывающие вибрации от технологического оборудования, башни и мачты, испытывающие многократные воздействия порывов ветра и т.п.
В соответствии с характером последствий от нарушения эксплуатационных свойств конструкции расчет на усталость следует вести по первому предельному состоянию. Однако согласно временному режиму воздействия вибрационная нагрузка является нагрузкой нормальной эксплуатации. Поэтому напряжения в конструкции определяются от пониженной нормативной нагрузки, вызывающей усталость, по сечению нетто, без учета динамического коэффициента.
Максимальное в цикле нагружения значение одного из характерных компонентов напряжений, определяемого обычно по упрощенным формулам сопротивления материалов, сравнивается с условным пределом усталости, устанавливаемым на основе экспериментальных данных:
где Rn — условное расчетное сопротивление усталости, зависящее от типа стали и степени концентрации напряжений в проверяемой точке конструкции.
В нормах тип стали характеризуется нормативным значением временного сопротивления на разрыв Run, концентрация напряжений — номером группы элементов в таблице с набором характерных конструктивных узлов. Нормами установлено восемь групп — от первой до восьмой. Степень концентрации напряжений возрастает с ростом номера группы. Значение расчетного сопротивления Rvполучено из испытаний образцов с асимметрией цикла загружения р = omin/omax = -1 при п ~ 2-10 6 циклов. Поправка на иное число циклов в пределах 10 5
Расчет элементов стальных конструкций на прочность с учетом хрупкого разрушения (проверка на хладостойкость)
Существенный резерв надежности стальных конструкций обеспечивается пластическими свойствами материала. В случае одноосного растяжения при комнатной температуре образцы строительной стали могут удлиняться на 14—27% без нарушения сплошности.
Однако в реальных конструкциях сталь может разрушаться хрупко, без заметных пластических деформаций. Такой вид разрушения является чрезвычайно опасным в силу внезапности и приводит в большинстве случаев к авариям конструкций. Поэтому расчет элементов с учетом хрупкого разрушения производится по первому предельному состоянию, несмотря на то что потеря несущей способности в этом случае может произойти при нагрузках нормальной эксплуатации.
Для элементов из строительной стали основными факторами, способствующими хрупкому разрушению, являются пониженная температура эксплуатации, вид напряженного состояния, концентрация напряжений, ударный характер приложения нагрузки, наличие остаточных сварочных напряжений, дефекты структуры стали, появившиеся при ее производстве, сварке, термообработке и некоторые другие.
Доминирующим фактором является пониженная температура эксплуатации. В связи с этим сопротивление стальных конструкций хрупкому разрушению отождествляется с их хладостойкостью.
При разрушении стальных образцов принято различать вязкое (пластическое) разрушение с матовой, волокнистой поверхностью излома, хрупкое разрушение с поверхностью излома, имеющей характерный кристаллический блеск, и промежуточное квазихрупкое разрушение с одновременным присутствием в изломе обоих характерных признаков.
Температура, при которой происходит переход от вязкого разрушения к квазихрупкому, называется первой критической температурой t 1 . Вторая критическая температура t 2 соответствует переходу от квазихрупкого разрушения к хрупкому.
Нормами предписывается проверять прочность стальных элементов на хладостойкость при отрицательной расчетной температуре t , определяемой СНиП 2.01.01-82 по строительной климатологии и геофизике как средняя минимальная температура наиболее холодной пятидневки в году.
Проверку следует делать для центрально растянутых элементов, а также для зон растяжения изгибаемых, внецентренно растянутых и внецентренно сжатых стержней при напряжении в них smах, вычисленном по расчетным нагрузкам без учета динамического коэффициента и превышающем 40 % расчетного сопротивления по пределу текучести, т.е. при smах>0,4Ry. Проверочная формула имеет вид
где Ru , gu , gс — соответственно расчетное сопротивление стали по пределу прочности и соответствующие коэффициенты условия работы (gu = 1,3);
b — коэффициент понижения расчетного сопротивления, учитывающий возможность хрупкого разрушения стали.
На основании экспериментальных данных в этом интервале температур принято линейное изменение b от 1 до 0,7 — 0,8:
коэффициент α принимается равным 0,2 для сталей С345, С375 при толщине проката tt >20 мм; 0,3 — для сталей С245 —С285 при t>20 мм.
Как видно из последней формулы, чем тоньше прокат и выше качество материала, что свойственно низколегированным сталям повышенной и высокой прочности, тем выше их хладостойкость.
© 2014-2022 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.024)
Читайте также:
