Функция ферми дирака для электронов в металле
Функция распределения для вырожденного коллектива фермионов впервые была получена итальянским физиком Энрико Ферми и английским физиком Полем Дираком:
Химический потенциал μ для фермионов обычно называют энергией, или уровнем Ферми – ЕФ.
Анализ выражения показывает, что при Е=ЕФ и температуре Т>0, fФ(Е)=½, т.е. вероятность заселения уровня Ферми при Т>0 равна ½.
Для того чтобы понять свойства функции Ферми-Дирака, полезно рассмотреть ее поведение при Т=0. Проводник можно представить в виде потенциальной ямы для электронов, выход из которой требует совершения работы по преодолению сил связи, удерживающих электроны – работы выхода (рис. 3.3, а). На рисунке показаны энергетические уровни, которые могут занимать электроны. Согласно постулату Паули, на каждом уровне может располагаться не более двух электронов (с противоположными спинами).
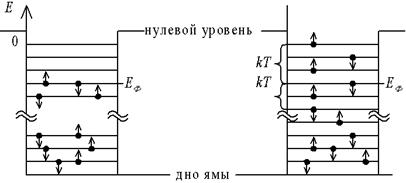
Как видно на рисунке, при Т=0 все уровни ниже уровня Ферми заняты, а все уровни выше этого уровня пусты, т.е. функция fФ(Е) при Т=0 имеет форму ступеньки (рис. 3.4, а).
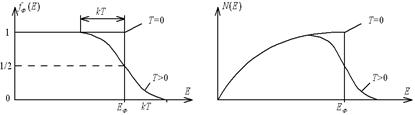
Рис. 3.4. Распределение Ферми-Дирака: а – функция распределения Ф-Д;
б – полная функция распределения
Таким образом можно определить физический смысл уровня Ферми, но только для проводников. В случае полупроводников или изоляторов это определение неприемлемо, поскольку в этих материалах недостаточно свободных электронов и уровень Ферми находится в запрещенной зоне (п. 4.5).
Умножив функцию распределения (3.20) на число состояний (3.13), получим выражение для полной функции распределения при Т=0 (рис. 3.4, б)
Проинтегрировав (3.21) в указанном интервале энергий, будем иметь выражение для энергии Ферми:
где n – концентрация электронного газа в проводнике.
Используя выражение (3.21), можно получить формулы для вычисления средней энергии – и максимальной скорости электронов при абсолютном нуле
Необходимо отметить, что кинетическая энергия электронов ЕФ не является тепловой энергией, а имеет чисто квантовую природу и определяется свойствами электронов как Ферми-частиц.
С повышением температуры электроны подвергаются тепловому возбуждению и переходят на более высокие энергетические уровни (см. рис. 3.3, б). Происходит “размывание” функций распределения (см. рис. 3.4), и ступенька Е=ЕФ преобразуется в интервал, ширина которого равна 2kT. Однако более глубокие состояния электронов остаются неизменными.
Проведенные расчеты показывают, что число термически возбужденных частиц составляет для комнатной температуры всего 1-2% от общего числа. Если проинтегрировать полную функцию распределения во всем энергетическом диапазоне, то можно получить выражение для температурной зависимости энергии Ферми
Напомним, что тепловое возбуждение так незначительно влияет на характеристики вырожденного Ферми-газа, что во многих случаях этим влиянием можно пренебречь и считать ЕФ = ЕФо во всем температурном диапазоне.
Можно также вычислить среднюю энергию электронов при ненулевой температуре Т>0
где Еп – полная энергия электронного газа.
Ранее мы говорили о Ферми-газе, считая его вырожденным коллективом. Однако, в случае выполнения критерия (3.11) G>>N, можно говорить о снятии вырождения. Тогда критерий невырожденности (3.11) примет вид
или в случае Е=0
Из последнего соотношения следует, что для невырожденного Ферми-газа должно выполняться условие
При выполнении условия (3.27) единицей в знаменателе выражения (3.20) можно пренебречь, и выражение (3.20) совпадает с формулой для функции Максвелла-Больцмана.
В проводниках, где концентрация электронов высока, электронный газ всегда находится в вырожденном состоянии. С невырожденным электронным газом приходится сталкиваться в собственных (беспримесных) и слаболегированных (10 16 . 10 24 м -3 ) полупроводниках. При таких условиях выполняется критерий (3.11) и электронный газ млжно считать невырожденным. Поэтому уместно, на наш взгляд, привести таблицу, где содержатся основные характеристики электронного газа: его средняя энергия, квадратичная скорость υкв, импульс P (табл. 3.2).
Параметры электронного газа [15]
| Параметры газа | Газ |
| невырожденный | вырожденный |
| , Т=0 Т>0 | |
| Jкв, Т=0 Т>0 | м/с |
| Р, Т=0 Т>0 | ≈10 10 Па Р ≈ Р0 |
Из данных таблицы видно, что параметры вырожденного газа в отличие от газа невырожденного при нулевой температуре не равны нулю и практически не зависят от температуры. Это, в свою очередь, говорит о нетепловом квантовомеханическом характере данных процессов.
Функция распределения Ферми-Дирака. Энергия Ферми
Исследование распределения Ферми-Дирака. Энергия Ферми
Энергия Фе́рми (E_F) системы невзаимодействующих фермионов — это увеличение энергии основного состояния системы при добавлении одной частицы. Это эквивалентно химическому потенциалу системы в ее основном состоянии при абсолютном нуле температур. Энергия Ферми может также интерпретироваться как максимальная энергия фермиона в основном состоянии при абсолютном нуле температур. Энергия Ферми — одно из центральных понятий физики твёрдого тела.
Физический смысл уровня Ферми: вероятность обнаружения частицы на уровне Ферми составляет 1/2 при любых температурах, кроме T = 0 (это физический смысл химического потенциала, для энергии Ферми это не верно).
Название дано в честь итальянского физика Энрико Ферми.
Фермионы — частицы с полуцелым спином, обычно 1/2, такие как электроны — подчиняются принципу запрета Паули, согласно которому две одинаковые частицы, образуя квантово-механическую систему (например, атом), не могут принимать одно и то же квантовое состояние. Следовательно, фермионы подчиняются статистике Ферми — Дирака. Основное состояние невзаимодействующих фермионов строится начиная с пустой системы и постепенного добавления частиц по одной, последовательно заполняя состояния в порядке возрастания их энергии (например, заполнение электронами электронных орбиталей атома). Когда необходимое число частиц достигнуто, энергия Ферми равна энергии самого высокого заполненного состояния (или самого низкого незанятого состояния: в случае макроскопической системы различие не важно). Поэтому энергию Ферми называют также уровнем Фе́рми. Частицы с энергией, равной энергии Ферми, двигаются со скоростью, называемой скоростью Фе́рми (только в случае изотропного дисперсионного соотношения в среде).
В свободном электронном газе (квантово-механическая версия идеального газа фермионов) квантовые состояния могут быть помечены согласно их импульсу. Нечто подобное можно сделать для периодических систем типа электронов, движущихся в атомной решётке металла, используя так называемый квазиимпульс (Частица в периодическом потенциале). В любом случае, состояния с энергией Ферми расположены на поверхности в пространстве импульсов, известной как поверхность Ферми. Для свободного электронного газа, поверхность Ферми — поверхность сферы; для периодических систем она вообще имеет искаженную форму. Объём, заключённый под поверхностью Ферми, определяет число электронов в системе, и её топология непосредственно связана с транспортными свойствами металлов, например, электрической проводимостью. Поверхности Ферми большинства металлов хорошо изучены экспериментально и теоретически.
Определение собственного полупроводника. Возникновение электропроводности собственного полупроводника с точки зрения модельных представлений и зонной теории. Расчет концентрации электронов в зоне проводимости произвольного полупроводника.
Собственный полупроводник-это чистый полупроводник, содержание посторонних примесей в котором не превышает 10−8 … 10−9%. Концентрация дырок в нём всегда равна концентрации свободных электронов, так как она определяется не легированием, а собственными свойствами материала, а именно термически возбуждёнными носителями, излучением и собственными дефектами.
Полупроводник без примесей обладает собственной электропроводностью, которая имеет два вклада: электронный и дырочный. Если к полупроводнику не приложено напряжение, то электроны и дырки совершают тепловое движение и суммарный ток равен нулю. При приложении напряжения в полупроводнике возникает электрическое поле, которое приводит к возникновению тока, называемого дрейфовым током iдр. Полный дрейфовый ток является суммой двух вкладов из электронного и дырочного токов:
iдр= in+ ip,
где индекс n соответствует электронному вкладу, а p - дырочному.
В полупроводниках при повышении температуры вследствие генерации электрон-дырочных пар концентрация электронов в зоне проводимости и дырок в валентной зоне увеличивается значительно быстрее, нежели уменьшается их подвижность, поэтому с повышением температуры проводимость растет. Процесс гибели электрон-дырочных пар называется рекомбинацией. Фактически проводимость собственного полупроводника сопровождается процессами рекомбинации и генерации и если скорости их равны, то говорят что полупроводник находится в равновесном состоянии.
Количество разрешённых состояний для электронов в зоне проводимости (определяемая плотностью состояний) и вероятность их заполнения (определяемая функцией Ферми — Дирака) и соответственные величины для дырок задают количество собственных электронов и дырок в полупроводнике:
n=Nc*exp((Ec-Ef)/kT)
p=Nv*exp((Ev-Ef)/kT)
где Nc, Nv — константы определяемые свойствами полупроводника, Ec и Ev — положение дна зоны проводимости и потолка валентной зоны соответственно,Ef- неизвестный уровень Ферми, k — постоянная Больцма
19 Скорость генерации. Тепловая генерация. Скорость рекомбинации. Коэффициент рекомбинации. Равновесное и стационарное состояния. Избыточная концентрация. Закон убыли избыточной концентрации со временем. Время жизни неосновных носителей. Графики Dр(t), р(t) (или Dn(t), n(t).
Под действием приложенного к кристаллу напряжения в нем возникает электрическое поле. Движение носителей заряда упорядочивается: электроны перемещаются по направлению к положительному электроду, дырки – к отрицательному. При этом не прекращается и тепловое движение носителей заряда, вследствие которого происходят столкновения их с атомами полупроводника и примеси.
Направленное движение носителей заряда под действием сил электрического поля называют дрейфом, а вызванный этим движением ток – дрейфовым током. При этом характер тока может быть электронным, если он вызван движением электронов, или дырочным, если он создается направленным перемещением дырок.
Средняя скорость носителей заряда в электрическом поле прямо пропорциональна напряженности электрического поля:
Коэффициент пропорциональности m называют подвижностью электронов (mn), или дырок (mp). Свободные электроны движутся в пространстве между узлами кристаллической решетки, а дырки – по ковалентным связям, поэтому средняя скорость, а следовательно, и подвижность электронов больше, чем дырок. У кремния подвижность носителей заряда меньше, чем у германия.
В собственных полупроводниках концентрации электронов и дырок одинаковы, но вследствие их разной подвижности электронная составляющая тока больше дырочной. В примесных полупроводниках концентрации электронов и дырок существенно отличаются, характер тока определяется основными носителями заряда: в полупроводниках р-типа – дырками, а в полупроводниках n-типа – электронами.
При неравномерной концентрации носителей заряда вероятность их столкновения друг с другом больше в тех слоях полупроводника, где их концентрация выше. Совершая хаотическое тепловое движение, носители заряда отклоняются в сторону, где меньше число столкновений, т.е. движутся в направлении уменьшения их концентрации.
Направленное движение носителей заряда из слоя с более высокой их концентрацией в слой, где концентрация ниже, называют диффузией, а ток, вызванный этим явлением, – диффузионным током. Этот ток, как и дрейфовый, может быть электронным или дырочным.
Степень неравномерности распределения носителей заряда характеризуется градиентом концентрации; его определяют как отношение изменения концентрации к изменению расстояния, на котором оно происходит. Чем больше градиент концентрации, т.е. чем резче она изменяется, тем больше диффузионный ток.
Электроны, перемещаясь из слоя с высокой концентрацией в слой с более низкой концентрацией, по мере продвижения рекомбинируют с дырками, и наоборот, диффундирующие в слой с пониженной концентрацией дырки рекомбинируют с электронами. При этом избыточная концентрация носителей заряда уменьшается.
Статистика Фе́рми — Дира́ка в статистической физике — квантовая статистика, применяемая к системам тождественных фермионов (как правило, частиц с полуцелым спином, подчиняющихся принципу запрета Паули, то есть, одно и то же квантовое состояние не может занимать более одной частицы); определяет распределение вероятностей нахождения фермионов на энергетических уровнях системы, находящейся в термодинамическом равновесии; предложена в 1926 году итальянским физиком Энрико Ферми и одновременно английским физиком Полем Дираком, который выяснил её квантово-механический смысл; позволяет найти вероятность, с которой фермион занимает данный энергетический уровень.
Работы по статистике Ферми — Дирака были опубликованы в 1926 году, а в 1927 она была применена Арнольдом Зоммерфельдом к электронам в металле.
В статистике Ферми — Дирака среднее число частиц в состоянии с энергией,
(число состояний с энергиейпри абсолютном нуле температуры),
В (идеальном) ферми-газе в пределе низких температур ), функция распределения частиц называется функцией Ферми:
распределением Ферми — Дирака. Для фиксированной температуры есть вероятность того, что состояние с энергиейОбратите внимание, что энергетический уровень . Теперь можно произвести простую модификацию:
.
Энергия Фе́рми ( ) системы невзаимодействующих фермионов — это увеличение энергии основного состояния системы при добавлении одной частицы. Это эквивалентно химическому потенциалу системы в ее основном состоянии приабсолютном нуле температур. Энергия Ферми может также интерпретироваться как максимальная энергия фермиона в основном состоянии при абсолютном нуле температур. Энергия Ферми — одно из центральных понятий физики твёрдого тела.
При ненулевой температуре ферми-газ не будет являться вырожденным, и населённость уровней будет плавно уменьшаться от нижних уровней к верхним.
В качестве уровня Ферми можно выбрать уровень, заполненный ровно наполовину (то есть вероятность находящегося на искомом уровне состояния быть заполненным частицей должна быть равна 1/2).
Энергия Ферми свободного ферми-газа связана с химическим потенциалом уравнением
где — постоянная Больцмана, и . Характерная температура имеет порядок 10 5 K для металла, следовательно при комнатной температуре (300 K), энергия Ферми и химический потенциал фактически эквивалентны. Это существенно, потому что химический потенциал не является энергией Ферми, которая входит в распределение Ферми — Дирака.
13. Идеальный Ферми-газ. Связь энергии Ферми и концентрации электронов. Средняя энергия электрона.
Фе́рми-газ(или идеальный газ Фе́рми — Дира́ка) — газ, состоящий из частиц, удовлетворяющих статистике Ферми — Дирака, имеющих малую массу и высокую концентрацию. Например, электроны в металле. В первом приближении можно считать, что потенциал, действующий на электроны в металле, является постоянной величиной и благодаря сильному экранированию положительно заряженными ионами можно пренебречь электростатическим отталкиванием между электронами. Тогда электроны металла можно рассматривать как идеальный газ Ферми — Дирака.
Вопрос 14. Виды связей атомов и молекул в кристаллах. Аморфное и кристаллическое состояния. Кристаллическая решетка. Период решетки.
В кристаллах имеют место следующие типы связей:
● Ковалентная связь;
● Ионная связь;
● Металлическая связь;
● Молекулярная связь;
● Водородная связь.
Рассмотрим их подробнее.
Ковалентная связь
Нейтральные атомы размещены в узлах кристаллической решётки. Связь образуется направленными валентными электронными облаками.
.Ионная связь
В узлах кристаллической решетки помещаются положительно и отрицательно заряженные ионы. Силы взаимодействия между узлами являются в основном электростатическими (кулоновскими). Связь между такими частицами называется гетерополярной или ионной.
Кристаллы с ионной связью при низких температурах являются диэлектриками. При тепературах близких к температуре плавления они становятся проводниками электричества. Примером кристаллов с ионной решёткой являются кристаллы каменной соли (NaCl).
Металлическая связь
Во всех узлах кристаллической решетки расположены положительные ионы металла. Между ними беспорядочно, подобно молекулам газа, движутся электроны, отщепившиеся от атомов при образовании ионов. Эти электроны играют роль цемента, удерживая вместе положительные ионы; в противном случае решетка распалась бы под действием сил отталкивания между ионами. Вместе с тем и электроны удерживаются ионами в пределах кристаллической решётки и не могут её покинут
Молекулярная связь
В узлах кристаллической решетки помещаются определенным образом ориентированные молекулы. Силы связи между молекулами в кристалле имеют ту же природу, что и силы притяжения между молекулами, приводящие к отклонению газов от идеальности. По этой причине их называют вандерваальсовскими силами.
Для кристаллов с молекулярными связями характерны низкие температуры плавления и высокая сжимаемость.
Водородная связь
Водородные связи, образуемые молекулами воды, обусловливают удивительно высокие точки плавления льда и кипения воды, существование максимума плотности воды, расширение воды при замерзании. Многие особые свойства неорганических и органических молекул, например димеризация жирных кислот, объясняются образованием водородных связей. Водородная связь – особенно важная структура белков особенность белков и нуклеиновых кислот.
Молекулярные связи образуют, например, следующие вещества: H2, N2, O2, CO2, H2O.
Аморфное состояние (от греч. а — отрицательная частица и morphē — форма)
твёрдое состояние вещества, обладающее двумя особенностями: его свойства (механические,тепловые, электрические и т. д.) в естественных условиях не зависят от направления в веществе (изотропия);при повышении температуры вещество, размягчаясь, переходит в жидкое состояние постепенно, т. е. в А. с.отсутствует определённая точка плавления.
Эти особенности обусловлены отсутствием в А. с. дальнего порядка — характерной для кристаллов
Кристалическое состояние вещества, характеризуется наличием дальнего порядка в расположении частиц (атомов, ионов, молекул). ВК. с. существует и ближний порядок, к-рый характеризуется постоянными координац. числами, валентнымиуглами и длинами хим. связей. Инвариантность характеристик ближнего порядка в К. с. приводит ксовпадению структурных ячеек при их трансляционном перемещении и образованию трехмернойпериодичности структуры (см. Кристаллохимия. Кристаллы). Вследствие своей макс. упорядоченности К. с.в-ва характеризуется миним. внутр. энергией и является термодинамически равновесным состоянием приданных параметрах -давлении, т-ре, составе (в случае твердых растворов) и др. Строго говоря, полностьюупорядоченное К. с. реально не м. б. осуществлено, приближение к нему имеет место при стремлении т-ры кО К (т. наз. идеальный кристалл). Реальные тела в К. с. всегда содержат нек-рое кол-во дефектов,нарушающих как ближний, так и дальний порядок. Особенно много дефектов наблюдается в твердых р-рах, вк-рых отдельные частицы и их группировки статистически занимают разл. положения в пространстве.Пери́од кристалли́ческой решётки — длина ребра элементарной ячейки кристаллической решётки. Для самой простой идеальной одноатомной кубической решетки это просто расстояние между соседними атомами. В общем случае — это наименьшее расстояние, при сдвиге на которое решетка точно воспроизводит свой исходный вид, то есть в каждом её узле оказываются такие же атомы, что и до сдвига.
Кристалли́ческая решётка — вспомогательный геометрический образ, вводимый для анализа строения кристалла. Решётка имеет сходство с канвой или сеткой, что даёт основание называть точки решётки узлами. Решёткой является совокупность точек, которые возникают из отдельной произвольно выбранной точки кристалла под действием группы трансляции. Это расположение замечательно тем, что относительно каждой точки все остальные расположены совершенно одинаково. Применение к решётке в целом любой из присущих ей трансляций приводит к её параллельному переносу и совмещению. Для удобства анализа обычно точки решётки совмещают с центрами каких-либо атомов из числа входящих в кристалл, либо с элементами симметрии.
ВОПРОС 15 Модель Кронига-Пени. Волновая функция электрона. Энергетические зоны. Классификация кристаллов по структуре энергетических зон. Зона проводимости и валентная зона. Эффективная масса электрона и дырки.
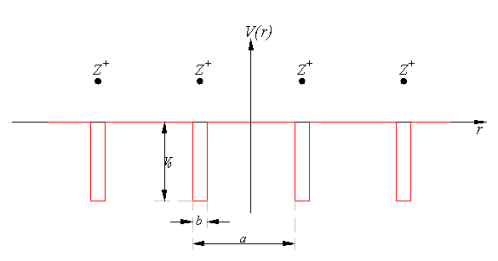
Модель Кронига — Пенни.Волнова́я фу́нкция, или пси-функция
где — волновая функция в координатном представлении.
Физический смысл волновой функции заключается в том, что согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точке конфигурационного пространства в данный момент времени считается равнойквадрату абсолютного значения волновой функции этого состояния в координатном представлении.
ЭНЕРГЕТИЧЕСКАЯ ЗОНАквазинепрерывная совокупность одночастичных состояний в энергетич. спектре конденсированной среды (вчастности, твёрдого тела). Возникновение зон можно объяснить, рассматривая либо движение частицы впериодич. поле (приближение слабой связи), либо модификацию энергетич. уровней атомов при ихсближении.
Кристаллические структуры делят на гомодесмические (координационные) и гетеродесмические. В первых все атомы соединены одинаковыми химическими связями, образующими пространственный каркас (напр. , алмаз, галогениды щелочных металлов) . Для вторых характерно наличие структурных фрагментов, внутри которых атомы соединены наиболее прочными (чаще всего ковалентными) связями; атомы, принадлежащие различным фрагментам, связаны существенно слабее. Фрагменты могут представлять собой конечные группировки атомов ("острова"), цепи, слои, каркасы; соотв. выделяют островные, цепочечные, слоистые и каркасные кристаллическая структура Островными кристаллическая структура обладают почти все органические соединения, а также галогены По характеру связи между атомами или структурными фрагментами различают ковалентные кристаллы, ионные кристаллы, металлические кристаллы и ван-дер-ваальсовы кристаллы.
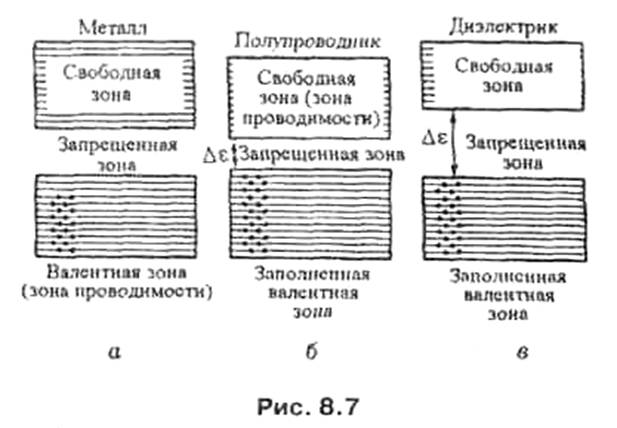
Зона проводимости — в зонной теории твёрдого тела первая из незаполненных электронами зон (диапазонов энергии, где могут находиться электроны) в полупроводниках и диэлектриках. Электроны из валентной зоны, преодолев запрещённую зону, при ненулевой температуре попадают в зону проводимости и начинают участвовать в проводимости, то есть перемещаться под действием электрического поля.
Валентная зона — энергетическая область разрешённых электронных состояний в твёрдом теле, заполненная валентными электронами.
В полупроводниках при T=0 (T — абсолютная температура) валентная зона заполнена электронами целиком, и электроны не дают вклада в электропроводность и другие кинетические эффекты, вызываемые внешними полями. При T>0 К происходит тепловая генерация носителей заряда, в результате которой часть электронов переходит в расположенную выше зону проводимости или на примесные уровни в запрещённой зоне. При этом в валентной зоне образуются дырки, участвующие наряду с электронами в зоне проводимости в переносе электрического тока. Дырки в валентной зоне могут также возникать при нетепловом возбуждении полупроводника — освещении, облучении потоком ионизирующих частиц, воздействии сильного электрического поля, который вызывает лавинный пробойполупроводника, и т. п.
свободный электрон некоторой массы , определяемой соотношением Значение массы носит название эффективной массы электрона в решетке.
Для свободного электрона, энергия которого определяется как , p * > 0, e > 0.
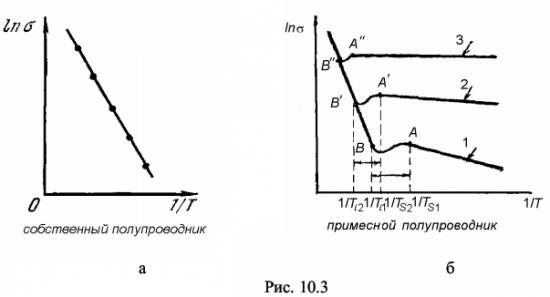
ВОПРОС 16. Определение собственного полупроводника. Возникновение электропроводности собственного полупроводника с точки зрения модельных представлений и зонной теории. Условие электронейтральности. Графикиn = f(T), f(Т), Lnf(1/T)Экспериментальное определение ширины ЗЗ.
Собственный полупроводник или полупроводник i-типа или нелегированный полупроводник (англ. intrinsic — собственный) — это чистый полупроводник, содержание посторонних примесей в котором не превышает 10 −8 … 10 −9 %. Концентрация дырок в нём всегда равна концентрации свободных электронов, так как она определяется не легированием, а собственными свойствами материала, а именно термически возбуждёнными носителями, излучением и собственными дефектами.
Энергетическая диаграмма, иллюстрирую-щая собственную электропроводность полупроводника при разрушении ковалентной связи
Как во всем кристалле, так и в любом физически малом объеме вещества суммарный заряд всех заряженных частиц должен быть равен нулю—это и есть условие электронейтральности, справедливое для незаряженного в целом тела.
ВОПРОС 17.Определение донорного полупроводника и донорной примеси. Электропроводность донорного полупроводника при высокой и низкой температурах. Температура примесного истощения. Условие электронейтральности. Графики n = f(T), f(Т), Lnf(1/T). в широком интервале температур.
Примеси, увеличивающие число свободных электронов, называют донорными или просто донорами. ДОНОРНАЯ ПРИМЕСЬ - примесь в полупроводнике, ионизация к-рой приводит к переходу электрона в зону проводимости или на уровень акцепторной примеси.
Температура, при которой F=Ed носит название температуры истощенияTs Как во всем кристалле, так и в любом физически малом объеме вещества суммарный заряд всех заряженных частиц должен быть равен нулю—это и есть условие электронейтральности, справедливое для незаряженного в целом тела.
ВОПРОС 18. Определение акцепторного полупроводника и акцепторной примеси. Электропроводность акцепторного полупроводника при высокой и низкой температурах. Температура примесного истощения. Условие электронейтральности. Графики n = f(T), f(Т), Lnf(1/T) в широком интервале температур.
АКЦЕПТОРНАЯ ПРИМЕСЬ (от лат. acceptor - принимающий) - примесь в полупроводнике, ионизация к-рой сопровождается захватом электронов из валентной зоны или с донорной примеси.В невырожденном акцепторном полупроводнике при температуре абсолютного нуля уровень Ферми лежит посередине между потолком валентной зоны и уровнем акцепторной примеси. При повышении температуры уровень Ферми также стремится к середине запрещенной зоны. В соответствии с положением уровня Ферми концентрация свободных дырок вначале растет по мере ионизации примеси (при этом концентрация свободных электронов пренебрежимо мала).
В акцепторном полупроводнике, как и в случае донорной примеси, при повышении температуры наступает область истощения, характеризующаяся полной ионизацией атомов акцепторной примеси. С дальнейшим ростом температуры уровень Ферми поднимается к середине запрещенной зоны и полупроводник ведет себя как собственный.
Уровень Ферми
Фе́рми-эне́ргия — значение энергии, ниже которой при температуре абсолютного нуля Т=0 К, все энергетические состояния системы частиц, подчиняющихся Ферми — Дирака статистике, заняты, а выше — свободны. Уровень Ферми — некоторый условный уровень, соответствующий энергии Ферми системы фермионов; в частности электронов твердого тела, играет роль химического потенциала для незаряженных частиц. Статистический смысл уровня Ферми — при любой температуре его заселенность равна 1/2.
Положение уровня Ферми является одной из основных характеристик состояния электронов (электронного газа) в твердом теле. В квантовой теории вероятность заполнения энергетических состояний электронами, определяется функцией Ферми F(E):
Е — энергия уровня, вероятность заполнения которого определяется;
EF — энергия характеристического уровня, относительно которого кривая вероятности симметрична;
Т — абсолютная температура;
При абсолютном нуле из вида функции следует, что
То есть все состояния, лежащие ниже уровня Ферми, полностью заняты электронами, а выше него свободны.
Энергия Ферми EF — максимальное значение энергии, которое может иметь электрон при температуре абсолютного нуля. Энергия Ферми совпадает со значениями химического потенциала газа фермионов при Т =0 К, то есть уровень Ферми для электронов играет роль уровня химического потенциала для незаряженных частиц. Соответствующий ей потенциал jF = EF/е называют электрохимическим потенциалом.
Таким образом, уровнем Ферми или энергией Ферми в металлах является энергия, которую может иметь электрон при температуре абсолютного нуля. При нагревании металла происходит возбуждение некоторых электронов, находящихся вблизи уровня Ферми (за счет тепловой энергии, величина которой порядка kT). Но при любой температуре для уровня с энергией, соответствующей уровню Ферми, вероятность заполнения равна 1/2. Все уровни, расположенные ниже уровня Ферми, с вероятностью больше 1/2 заполнены электронами, а все уровни, лежащие выше уровня Ферми, с вероятностью больше1/2 свободны от электронов.
Для электронного газа в металлах при Т = 0 величина энергии Ферми однозначно определяется концентрацией электронов и ее можно выразить через число n частиц электронного газа в единице объема: зависимость энергии Ферми от концентрации электронов нелинейная.
С ростом температуры (а также уменьшением концентрации электронов) уровень Ферми смещается по шкале энергий влево, но его заселенность остается равной 1/2. В реальных условиях изменение EFсувеличением температуры мало. Например, для Ag, имеющего при Т=0 значение EF равное 5,5 эВ, изменение энергии Ферми при температуре плавления составляет всего около 0,03% от исходного значения.
В полупроводниках при очень низких температурах уровень Ферми лежит посередине между дном зоны проводимости и потолком валентной зоны. (Для донорных полупроводников — полупроводников n-типа проводимости — уровень Ферми лежит посередине между дном зоны проводимости и донорным уровнем). С повышением температуры вероятность заполнения донорных состояний уменьшается, и уровень Ферми перемещается вниз. При высоких температурах полупроводник по свойствам близок к собственному, и уровень Ферми устремляется к середине запрещенной зоны. Аналогичные закономерности проявляются и полупроводниках р-типа проводимости.
Существование энергии Ферми является следствием Принципа Паули. Величина энергии Ферми существенно зависит от свойств системы. Понятие об энергии Ферми используется в физике твердого тела, в ядерной физике, в астрофизике и т. д.
Вероятность нахождения электрона на том или ином энергетическом уровне при температуре Т определяется функцией Ферми – Дирака:
Читайте также:
