Электронная теория проводимости металлов
Электропроводность твердых тел обусловлена коллективным направленным движением свободных электронов.
К концу XIX века ученые знали связь между электрическим сопротивлением, силой тока и напряжением, которая описывается законом Ома. Благодаря эффекту Холла знали они и то, что носителями электрического тока в металлах являются отрицательно заряженные электроны. Оставалось составить описание электрического сопротивления на атомном уровне. Первую попытку такого рода предпринял в 1900 году немецкий физик Пауль Друде (Paul Drude, 1863–1906).
Смысл электронной теории проводимости сводится к тому, что каждый атом металла отдает валентный электрон из внешней оболочки, и эти свободные электроны растекаются по металлу, образуя некое подобие отрицательно заряженного газа. Атомы металла при этом объединены в трехмерную кристаллическую решетку, которая практически не препятствует перемещению свободных электронов внутри нее (см. Химические связи). Как только к проводнику прикладывается электрическая разность потенциалов (например, посредством замыкания на два его конца двух полюсов аккумуляторной батареи), свободные электроны приходят в упорядоченное движение. Сначала они движутся равноускоренно, но длится это недолго, поскольку очень скоро электроны перестают ускоряться, сталкиваясь с атомами решетки, которые, в свою очередь, от этого начинают колебаться всё с большей амплитудой относительно условной точки покоя, и мы наблюдаем термоэлектрический эффект разогревания проводника.
На электроны же эти столкновения оказывают затормаживающее воздействие, аналогично тому, как, допустим, человеку тяжело с достаточно большой скоростью передвигаться в плотной людской толпе. В результате скорость электронов устанавливается на некоей усредненной отметке, которая называется скоростью миграции, и скорость эта, на самом деле, отнюдь не высока. Например, в обычной бытовой электропроводке средняя скорость миграции электронов составляет всего несколько миллиметров в секунду, то есть, электроны отнюдь не летят по проводам, а скорее ползут по ним темпами, достойными разве что улитки. Свет же в лампочке зажигается практически моментально лишь потому, что с места все эти медлительные электроны трогаются одновременно, как только вы нажимаете на кнопку выключателя, и электроны в спирали лампочки также приходят в движение сразу же. То есть, нажимая на кнопку выключателя, вы производите в проводах эффект, аналогичный тому, как если бы включили насос, подсоединенный к поливочному шлангу, до отказа заполненному водой, — струя на противоположном от насоса конце хлынет из шланга незамедлительно.
Друде весьма серьезно подошел к описанию свободных электронов. Он предположил, что внутри металла они ведут себя подобно идеальному газу, и применил к ним уравнение состояния идеального газа, достаточно справедливо проведя аналогию между соударениями электронов и тепловыми соударениями молекул идеального газа. Это позволило ему сформулировать формулу электрического сопротивления, как функции среднего времени между соударениями свободных электронов с атомами кристаллической решетки. Подобно многим простым теориям, электронная теория проводимости хорошо описывает некоторые основные явления из области электропроводности, но бессильна описать многие нюансы этого явления. В частности, она не только не объясняет явления сверхпроводимости при сверхнизких температурах (см. Теория сверхпроводимости, но, напротив, предсказывает неограниченный рост электрического сопротивления любого вещества при стремлении его температуры к абсолютному нулю. Поэтому сегодня электропроводящие свойства вещества принято интерпретировать в рамках квантовой механики (см. Уравнение Шрёдингера).
Электрический ток в металлах
Электрическим током в металлах называют упорядоченное движение электронов под действием электрического поля.
Исходя из опытов, видно, что металлический проводник вещество не переносит, то есть ионы металла не участвуют в передвижении электрического заряда.
Носители тока в металлах
При исследованиях были получены доказательства электронной природы тока в металлах. Еще в 1913 году Л.И. Мандельштам и Н.Д. Папалекси выдали первые качественные результаты. А в 1916 году Р. Толмен и Б. Стюарт модернизировали имеющуюся методику и выполнили количественные измерения, которые доказывали, что движение электронов происходит под действием тока в металлических проводниках.
Рисунок 1 . 12 . 1 показывает схему Толмена и Стюарта. Катушка, состоящая из большого количества витков тонкой проволоки, приводилась в действие при помощи вращения вокруг своей оси. Ее концы были прикреплены к баллистическому гальванометру Г. Производилось резкое торможение катушки, что было следствием возникновения кратковременного тока, обусловленного инерцией носителя заряда. Измерение полного заряда производилось при помощи движения стрелок гальванометра.
Рисунок 1 . 12 . 1 . Схема опыта Толмена и Стюарта.
Во время торможения вращающейся катушки сила F = - m d υ d t , называемая тормозящей, действовала на каждый носитель заряда е . F играла роль сторонней силы, иначе говоря, неэлектрического происхождения. Именно эта сила, характеризующаяся единицей заряда, является напряженностью поля сторонних сил E с т :
E с т = - m e d υ d t .
То есть при торможении катушки происходит возникновение электродвижущей силы δ , равной δ = E с т l = m e d υ d t l , где l – длина проволоки катушки. Определенный промежуток времени процесса торможения катушки обусловлен протеканием по цепи заряда q :
q = ∫ I d t = 1 R ∫ δ d t = m e l υ 0 R .
Данная формула объясняет, что l – это мгновенное значение силы тока в катушке, R – полное сопротивление цепи, υ 0 – начальная линейная скорость проволоки. Видно, что определение удельного заряда e m в металлах производится, исходя из формулы:
Величины, находящиеся с правой стороны, можно измерить. Основываясь на результатах опытов Толмена и Стюарта, установили, что носители свободного заряда имеют отрицательный знак, а отношение носителя в его массе близко по значению удельного заряда электрона, получаемого в других опытах. Было выявлено, что электроны – это носители свободных зарядов.
Современные данные показывают, что модуль заряда электрона, то есть элементарный заряд, равняется e = 1 , 60218 · 10 - 19 К л , а обозначение его удельного заряда – e m = 1 , 75882 · 10 11 К л / к г .
При наличии отличной концентрации свободных электронов есть смысл говорить о хорошей электропроводимости металлов. Это выявили еще перед опытами Толмена и Стюарта. В 1900 году П. Друде, основываясь на гипотезе о существовании свободных электронов в металлах, создал электронную теорию проводимости металлов. Ее развил и расширил Х. Лоренц, после чего она получила название классическая электронная теория. На ее основании поняли, что электроны ведут себя как электронный газ, похожий на идеальный по своему состоянию. Рисунок 1 . 12 . 2 показывает, каким образом он может заполнить пространство между ионами, которые уже образовали кристаллическую решетку металла.
Рисунок 1 . 12 . 2 . Газ свободных электронов в кристаллической решетке металла. Показана траектория одного из электронов.
Потенциальный барьер. Движение электронов в кристаллической решетке
После взаимодействия электронов с ионами первые покидают металл, преодолевая только потенциальный барьер.
Высота такого барьера получила название работы выхода.
Наличие комнатной температуры не позволяет электронам проходить этот барьер. Потенциальная энергия выхода электрона после взаимодействия с кристаллической решеткой намного меньше, чем при удалении электрона из проводника.
Расположение е в проводнике характеризуется наличием потенциальной ямы, глубина которой получила название потенциального барьера.
Ионы, образующие решетку, и электроны принимают участие в тепловом движении. Благодаря тепловым колебаниям ионов вблизи положений равновесий и хаотичному движению свободных электронов, при столкновении первых со вторыми происходит усиление термодинамического равновесия между электронами и решеткой.
По теории Друде-Лоренца имеем, что электроны имеют такую же среднюю энергию теплового движения, как и молекулы одноатомного идеального газа. Это делает возможным оценивание средней скорости υ т ¯ теплового движения электронов, используя молекулярно-кинетическую теорию.
Комнатная температура дает значение, равное 10 5 м / с .
Если наложить внешнее электрическое поле в металлический проводник, тогда произойдет тепловое упорядоченное движения электронов (электрический ток), то есть дрейф. Определение средней его скорости υ д ¯ выполняется по интервалу имеющегося времени ∆ t через поперечное сечение S проводника электронов, которые находятся в объеме S υ д ∆ t .
Количество таких е равняется n S υ д ∆ t , где n принимает значение средней концентрации свободных электронов, равняющейся числу атомов в единице объема металлического проводника. За имеющееся количество времени ∆ t через сечение проводника проходит заряд ∆ q = e n S υ д ∆ t .
Тогда I = ∆ q ∆ t = e n S υ д или υ д = I e n S .
Концентрация n атомов в металлах находится в пределах 10 28 - 10 29 м - 3 .
Формула дает возможность оценить среднюю скорость υ д ¯ упорядоченного движения электронов со значением в промежутке 0 , 6 - 6 м м / с для проводника с сечением 1 м м 2 и проходящим током в 10 А .
Средняя скорость υ д ¯ упорядоченного движения электронов в металлических проводниках на много порядков меньше скорости υ т их теплового движения υ д ≪ υ т .
Рисунок 1 . 12 . 3 демонстрирует характер движения свободного е , находящегося в кристаллической решетке.
Рисунок 1 . 12 . 3 . Движение свободного электрона в кристаллической решетке: а – хаотическое движение электрона в кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным электрическим полем. Масштабы дрейфа υ д ¯ ∆ t сильно преувеличены.
Наличие малой скорости дрейфа не соответствует опыту, когда ток всей цепи постоянного тока устанавливается мгновенно. Замыкание производится при помощи воздействия электрического поля со скоростью c = 3 · 10 8 м / с . По прошествии времени l c ( l - длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля. В ней происходит упорядоченное движение электронов.
Классическая электронная теория металлов предполагает, что их движение подчинено законам механики Ньютона. Данная теория характеризуется тем, что происходит пренебрежение взаимодействием электронов между собой, а взаимодействие с положительными ионами расценивается как соударения, при каждом из которых e сообщает накопленную энергию решетке. Поэтому принято считать, что после соударения движение электрона характеризуется нулевой дрейфовой скоростью.
Абсолютно все выше предложенные допущения приближенные. Это дает возможность объяснения законов электрического тока в металлических проводниках, основываясь на электронной классической теории.
Закон Ома
В промежутке между соударениями на электрон действует сила, равняющаяся по модулю e E , в результате чего получает ускорение e m E .
Конец свободного пробега характеризуется дрейфовой скоростью электрона, которую определяют по формуле
υ д = υ д m a x = e E m τ .
Время свободного пробега обозначается τ . Оно способствует упрощению расчетов для нахождения значения всех электронов. Средняя скорость дрейфа υ д равняется половине максимального значения:
υ д = 1 2 υ д m a x = 1 2 e E m τ .
Если имеется проводник с длиной l , сечением S с концентрацией электронов n , тогда запись нахождения тока в проводнике имеет вид:
I = e n S υ д = 1 2 e 2 τ n S m E = e 2 τ n S 2 m l U .
U = E l – это напряжение на концах проводника. Формула выражает закон Ома для металлического проводника. Тогда электрическое сопротивление необходимо находить:
R = 2 m e 2 n τ l S .
Удельное сопротивление ρ и удельная проводимость ν выражаются как:
ρ = 2 m e 2 n τ ; ν = 1 ρ = e 2 n τ 2 m .
Закон Джоуля-Ленца
Конец пробега электронов под действием поля характеризуется кинетической энергией
1 2 m ( υ д ) m a x 2 = 1 2 e 2 τ 2 m E 2 .
Исходя из предположений, энергия при соударениях передается решетке, а в последствии переходит в тепло.
Время ∆ t каждого электрона испытывается ∆ t τ соударений. Проводник с сечение S и длиной l имеет n S l электронов. Тогда выделившееся тепло в проводнике за ∆ t равняется
∆ Q = n S l ∆ t τ e 2 τ 2 2 m E 2 = n e 2 τ 2 m S l U 2 ∆ t = U 2 R ∆ t .
Данное соотношение выражает закон Джоуля-Ленца.
Благодаря классической теории, имеет место трактовка существования электрического сопротивления металлов, то есть законы Ома и Джоуля-Ленца. Классическая электронная теория не в состоянии ответить на все вопросы.
Она не способна объяснить разницу в значении молярной теплоемкости металлов и диэлектрических кристаллов, равняющейся 3 R , где R записывается как универсальная газовая постоянная. Теплоемкость металла не зависит от количества свободных электронов.
Классическая электронная теория не объясняет температурную зависимость удельного сопротивления металлов. По теории ρ ~ T , а исходя из экспериментов – ρ ~ T . Примером расхождения теории с практикой служит сверхпроводимость.
Сопротивление металлического проводника
Исходя из классической теории, удельное сопротивление металлов должно постепенно уменьшаться при понижении температуры, причем остается конечным при любой T . Данная зависимость характерна для проведения опытов при высоких температурах. Если T достаточно низкая, тогда удельное сопротивление металлов теряет зависимость от температуры и достигает предельного значения.
Особый интерес представило явление сверхпроводимости. В 1911 году его открыл Х. Каммерлинг-Оннес.
Если имеется определенная температура T к р , различная для разных веществ, тогда удельное сопротивление уменьшается до нуля с помощью скачка, как изображено на рисунке 1 . 12 . 4 .
Критической температурой для ртути считается значение 4 , 1 К , для алюминия – 1 , 2 К , для олова – 3 , 7 К . Наличие сверхпроводимости может быть не только у элементов, но и у химических соединений и сплавов. Ниобий с оловом Ni 3 Sn имеют критическую точку температуры в 18 К . Существуют вещества, которые при низкой температуре переходят в сверхпроводящее состояние, тогда как в обычных условиях ими не являются. Серебро и медь являются проводниками, но при понижении температуры сверхпроводниками не становятся.
Рисунок 1 . 12 . 4 . Зависимость удельного сопротивления ρ от абсолютной температуры T при низких температурах: a – нормальный металл; b – сверхпроводник.
Сверхпроводящее состояние говорит об исключительных свойствах вещества. Одним из важнейших является способность на протяжении длительного времени поддерживать электрический ток, возбужденный в сверхпроводящей цепи, без затухания.
Классическая электронная теория не может объяснить сверхпроводимость. Это стало возможным спустя 60 лет после его открытия, основываясь на квантово-механических представлениях.
Рост интереса к данному явлению увеличивался по мере появления новых материалов, способных обладать высокими критическими температурами. В 1986 было обнаружено сложное соединение с температурой T к р = 35 К . На следующий год сумели создать керамику с критической Т в 98 К , которая превышала Т жидкого азота ( 77 К ) .
Явление перехода веществ в сверхпроводящее состояние при Т , превышающих температуру кипения жидкого азота, называют высокотемпературной сверхпроводимостью.
Позже в 1988 году создали Tl - Ca - Ba - Cu - O соединение с критической Т , достигающей 125 К . На данный момент ученые заинтересованы в поиске новых веществ с наиболее высокими значениями T к р . Они рассчитывают на получение сверхпроводящего вещества при комнатной температуре. Если это будет сделано, произойдет революция в науке и технике. До настоящего времени все свойства и механизмы состава сверхпроводимых керамических материалов до конца не исследованы.
Электронная теория проводимости металлов
В 1900 году немецкий физик П. Друде создал теорию электропроводности металлов. В основе этой теории лежат следующие допущения:
- Свободные электроны в металлах ведут себя подобно молекулам идеального газа. Электронный газ подчиняется законам идеального газа.
- Движение свободных электронов подчиняется законам Ньютона.
- Свободные электроны в процессе хаотического движения сталкиваются только с ионами кристаллической решетки.
- При столкновении электронов с ионами электроны передают ионам свою кинетическую энергию полностью.
Согласно данной модели, на отрезке проводника свободные электроны совершают хаотическое тепловое движение. Действующее в проводнике электрическое поле перемещает электроны с небольшой скоростью (скорость дрейфа электронов ~ 0,1 мм/с) вдоль проводника.
Сила тока в проводнике:
где n – концентрация свободных электронов в проводнике
v> – средняя скорость дрейфа электронов
S – поперечное сечение проводника.
С позиции электронной проводимости металлов удалось объяснить причину нагревания проводников при прохождении электрического тока.
Электронная теория проводимости металлов экспериментально подтверждена в 1913 году российскими физиками Л.И. Мандельштамом и Н.Д. Папалекси и в 1916 году американскими физиками Т. Стюартом и Р. Толменом.
Направление электрического тока в проводнике выбрано в сторону движения положительно заряженных частиц.

Отношение заряда, переносимого через поперечное сечение проводника за интервал времени, к этому интервалу времени называется силой тока.
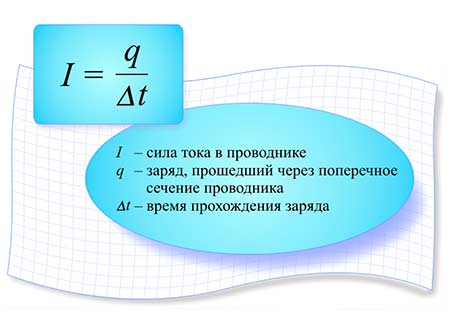
В СИ [I] = 1 А (Ампер)
Для поддержания электрического тока в проводнике необходимо электрическое поле. Его действие характеризуется электрическим напряжением.

В СИ [U] = 1 В (Вольт)
Для поддержания постоянного направленного движения заряженных частиц в проводнике электрическое поле должно совершать работу. Эту работу принято называть работой электрического тока.
Работа сил электрического поля или работа электрического тока на участке цепи сопротивлением R и за время t равна:

В СИ [A] = 1 Дж (Джоуль)
При нагревание проводника растет его температура, следовательно, увеличивается внутренняя энергия. С прекращением роста температуры проводника он начинает передавать окружающим телам некоторое количество теплоты, равное работе электрического тока. Таким образом, формула A=IUt определяет количество теплоты, переданное проводником другим телам.
Для последовательного соединения проводников удобнее воспользоваться формулой:
При параллельном соединении удобно использовать формулу:
Для характеристики электрических приборов удобнее пользоваться физической величиной, получившей название мощность тока.
Условия существования электрического тока в металлах
Электрический ток в металлах — это упорядоченное (направленное) движение электронов под действием электрического поля.
Особенность металлических проводников состоит в том, что заряд электричества переносят свободные электроны. Они перемещаются в одном направлении под влиянием внешнего электрического поля, создавая электрический ток.
Природа электрической проводимости у металлов обусловлена наличием кристаллической решётки, в узлах которой расположены положительные ионы, а в пространстве между ними движутся свободные электроны. Свободные электроны не связаны с ядрами своих атомов. Отрицательный заряд всех свободных электронов по модулю равен положительному заряду всех ионов решетки, таким образом проводник считается электрически нейтральным.
Кто открыл, опыт Мандельштама и Папалекси
Первые опыты по изучению электрической проводимости металлов провел немецкий ученый Карл Виктор Эдуард Рикке в 1901 году. Суть эксперимента сводилась к следующему. Три отполированных цилиндра плотно прижали друг к другу, расположив в таком порядке: медь–алюминий–медь. В течение года через них пропускали ток в одном и том же направлении.
Суммарный заряд, прошедший через этот проводник за все время составил более 3,5 МКл. После завершения опыта цилиндры взвесили и выяснилось, что их массы не изменились. Это исследование стало доказательством того, что прохождение тока в металлах не связано с химическими процессами и переносом вещества, а заряд создается частицами, которые имеются у всех металлов, т.е. электронами.
Опыты по изучению электропроводимости в 1916 году продолжили русские ученые Л. И. Мандельштам и Н. Д. Папалекси. Они задались целью узнать, имеется ли масса у электрона. Если электрон обладает массой, то должен подчиняться законам механики, в том числе, закону инерции. К примеру, если движущийся проводник резко остановить, то электроны еще какое-то время будут двигаться в том же направлении по инерции.
Была собрана следующая установка: катушка на стержне со скользящими контактами, которые присоединены к гальванометру. Катушка вращалась с большой скоростью, затем резко останавливалась, при этом фиксировали отклонение стрелки гальванометра. В ходе эксперимента ученые установили, что электрон обладает массой. Но измерить эту массу они не смогли, опыт был только качественным.
Спустя три года физики Р. Толмен и Б. Стюарт предложили свой вариант подобного эксперимента, что позволило произвести количественные измерения. Им удалось вычислить массу электрона. Для этого они измерили заряд на выходах катушки, образующийся при торможении. После внезапной остановки катушки в цепи возникал импульс тока. Направление тока указывало на то, что он вызван движением отрицательных зарядов.
С помощью баллистического гальванометра ученые измерили суммарный заряд, проходящий по цепи, и вычислили отношение заряда одной частицы к ее массе — q / m . Оно оказалось близким по значению к отношению e / m для электрона = 1 , 8 × 1011 К л / к г , которое на тот момент уже было известно.
Какие частицы его создают, скорость распространения тока
Хорошая электропроводность металлов обусловлена высокой концентрацией свободных электронов. Каждый атом металла, находящийся в узле кристаллической решетки, имеет один или несколько валентных (свободных) электронов. Валентные электроны находятся на внешней электронной оболочке и слабо связаны с ядром, поэтому атом легко с ними расстается.
Они совершают тепловое движение в различных направлениях по всему кристаллу. Положительные ионы остаются в узлах кристаллической решетки, а пространство между ними заполняется свободными электронами или так называемым электронным газом.
Если металлический проводник присоединить к источнику тока и замкнуть цепь, валентные электроны продолжают совершать хаотическое движение, но под действием возникшего внешнего электрического поля они также начинают перемещаться в одном направлении. Это упорядоченное течение электронного газа, совмещенное с тепловым движением электронов, и есть электрический ток в металле.
Скорость упорядоченного движения (дрейфовая скорость) любого электрона в проводнике не превышает 1 мм/с.
Скорость распространения электрического тока близка к скорости света в вакууме (300 000 км/с).
Одновременно с распространением электрического поля все электроны начинают двигаться в одном направлении по всей длине проводника.
Закон Ома и Джоуля-Ленца, формулы
Классическая электронная теория металлов берет за основу, что движение электронов подчиняется законам механики Ньютона. При этом не учитывают взаимодействие электронов между собой. Предполагается также, что при каждом столкновении с положительными ионами электрон передает решетке всю полученную в электрическом поле энергию, а затем начинает движение с нулевой дрейфовой скоростью.
Несмотря на эти особенности, законы электрического тока в металлических проводниках — Ома и Джоуля–Ленца — находятся в рамках классической электронной теорией.
Закон Ома
В 1827 году немецкий физик Георг Ом установил, что связь таких физических характеристик, как сила тока, напряжение и сопротивление определяется следующей зависимостью: для определенного участка цепи сила тока I прямо пропорциональна напряжению U и обратно пропорциональна электрическому сопротивлению R.
Закон Джоуля–Ленца
Так как проводник нагревается при протекании по нему электрического тока, то выделяется теплота. В 1841–1842 годах сразу два ученых независимо друг от друга Дж. Джоуль (Англия) и Э. Х. Ленц (Россия) экспериментально доказали, что количество выделяющейся теплоты Q прямо пропорционально квадрату тока I2, сопротивлению проводника R и времени t, в течение которого ток протекал по проводнику.
Q=I2Rt.
Проводник нагревается за счет работы сил электрического поля над носителями заряда. Эта работа A также равна Q: A=Q=I2Rt.
Применив закон Ома для участка однородной цепи и определение силы тока, можно получить следующие варианты формулы:
Читайте также:
