Прочность бетона при растяжении местном сжатии срезе двухосном и трехосном напряженном состоянии
Нормативные и расчетные характеристики бетона и арматуры
Основными показателями прочности и деформативности бетона являются нормативные значения их прочностных и деформационных характеристик.
Основными прочностными характеристиками бетона являются нормативные значения:
- сопротивления бетона осевому сжатию Rb,n;
- сопротивления бетона осевому растяжению Rbt,n.
Нормативное значение сопротивления бетона осевому сжатию (призменная прочность) следует устанавливать в зависимости от нормативного значения прочности образцов-кубов (нормативная кубиковая прочность) для соответствующего вида бетона и контролируемого на производстве.
Нормативное значение сопротивления бетона осевому растяжению при назначении класса бетона по прочности на сжатие следует устанавливать в зависимости от нормативного значения прочности на сжатие образцов-кубов для соответствующего вида бетона и контролируемого на производстве.
Соотношение между нормативными значениями призменной и кубиковой прочностями бетона на сжатие, а также соотношение между нормативными значениями прочности бетона на растяжение и прочности бетона на сжатие для соответствующего вида бетона следует устанавливать на основе стандартных испытаний.
При назначении класса бетона по прочности на осевое растяжение нормативное значение сопротивления бетона осевому растяжению принимают равным числовой характеристике класса бетона по прочности на осевое растяжение, контролируемой на производстве.
Основными деформационными характеристиками бетона являются нормативные значения:
- предельных относительных деформаций бетона при осевом сжатии и растяжении εbo,n и εbto,n ;
- начального модуля упругости бетона Е b,n .
- Кроме того, устанавливают следующие деформационные характеристики:
- начальный коэффициент поперечной деформации бетона v;
- модуль сдвига бетона G;
- коэффициент температурной деформации бетона αbt;
- относительные деформации ползучести бетона εсг (или соответствующие им характеристику ползучести φb,cr меру ползучести Cb,cr;
- относительные деформации усадки бетона εshr.
Нормативные значения деформационных характеристик бетона следует устанавливать в зависимости от вида бетона, класса бетона по прочности на сжатие, марки бетона по средней плотности, а также в зависимости от технологических параметров бетона, если они известны (состава и характеристики бетонной смеси, способов твердения бетона и других параметров).
В качестве обобщенной характеристики механических свойств бетона при одноосном напряженном состоянии следует принимать нормативную диаграмму состояния (деформирования) бетона, устанавливающую связь между напряжениями σ b,n (σbt,n) и продольными относительными деформациями εb,n (εbt,n) сжатого (растянутого) бетона при кратковременном действии однократно приложенной нагрузки (согласно стандартным испытаниям) вплоть до их нормативных значений.
Основными расчетными прочностными характеристиками бетона, используемыми в расчете, являются расчетные значения сопротивления бетона:
Расчетные значения прочностных характеристик бетона следует определять делением нормативных значений сопротивления бетона осевому сжатию и растяжению на соответствующие коэффициенты надежности по бетону при сжатии и растяжении.
Значения коэффициентов надежности следует принимать в зависимости от вида бетона, расчетной характеристики бетона, рассматриваемого предельного состояния, но не менее:
- для коэффициента надежности по бетону при сжатии:
- 1.3 - для предельных состояний первой группы;
- 1.0 - для предельных состояний второй группы;
- для коэффициента надежности по бетону при растяжении:
- 1,5 - для предельных состояний первой группы при назначении класса бетона по прочности на сжатие;
- 1.3 - то же, при назначении класса бетона по прочности на осевое растяжение;
- 1.0 - для предельных состояний второй группы.
Расчетные значения основных деформационных характеристик бетона для предельных состояний первой и второй групп следует принимать равными их нормативным значениям.
Влияние характера нагрузки, окружающей среды, напряженного состояния бетона, конструктивных особенностей элемента и других факторов, не отражаемых непосредственно в расчетах, следует учитывать в расчетных прочностных и деформационных характеристиках бетона коэффициентами условий работы бетона γbi.
Расчетные диаграммы состояния (деформирования) бетона следует определять путем замены нормативных значений параметров диаграмм на их соответствующие расчетные значения.
Значения прочностных характеристик бетона при плоском (двухосном) или объемном (трехосном) напряженном состоянии следует определять с учетом вида и класса бетона из критерия, выражающего связь между предельными значениями напряжений, действующих в двух или трех взаимно перпендикулярных направлениях.
Деформации бетона следует определять с учетом плоского или объемного напряженных состояний.
Характеристики бетона — матрицы в дисперсно-армированных конструкциях следует принимать как для бетонных и железобетонных конструкций.
Характеристики фибробетона в фибробетонных конструкциях следует устанавливать в зависимости от характеристик бетона, относительного содержания, формы, размеров и расположения фибр в бетоне, ее сцепления с бетоном и физико-механических свойств, а также в зависимости от размеров элемента или конструкции.
Основными показателями прочности и деформативности арматуры являются нормативные значения их прочностных и деформационных характеристик.
Основной прочностной характеристикой арматуры при растяжении (сжатии) является нормативное значение сопротивления Rs,n, равное значению физического предела текучести или условного, соответствующего остаточному удлинению (укорочению), равному 0,2%. Кроме того, нормативные значения сопротивления арматуры при сжатии ограничивают значениями, отвечающими деформациям, равным предельным относительным деформациям укорочения бетона, окружающего рассматриваемую сжатую арматуру.
Основными деформационными характеристиками арматуры являются нормативные значения:
- относительных деформаций удлинения арматуры εs0,n при достижении напряжениями нормативных значений Rs,n;
- модуля упругости арматуры Es,n.
Для арматуры с физическим пределом текучести нормативные значения относительной деформации удлинения арматуры εs0,n определяют как упругие относительные деформации при нормативных значениях сопротивления арматуры и ее модуля упругости.
Для арматуры с условным пределом текучести нормативные значения относительной деформации удлинения арматуры εs0,n определяют как сумму остаточного удлинения арматуры, равного 0,2%, и упругих относительных деформаций при напряжении, равном условному пределу текучести.
Для сжатой арматуры нормативные значения относительной деформации укорочения принимают такими же, как при растяжении, за исключением специально оговоренных случаев, но не более предельных относительных деформаций укорочения бетона.
Нормативные значения модуля упругости арматуры при сжатии и растяжении принимают одинаковыми и устанавливают для соответствующих видов и классов арматуры.
В качестве обобщенной характеристики механических свойств арматуры следует принимать нормативную диаграмму состояния (деформирования) арматуры, устанавливающую связь между напряжениями σs,n и относительными деформациями εs,n арматуры при кратковременном действии однократно приложенной нагрузки (согласно стандартным испытаниям) вплоть до достижения их установленных нормативных значений.
Диаграммы состояния арматуры при растяжении и сжатии принимают одинаковыми, за исключением случаев, когда рассматривается работа арматуры, в которой ранее были неупругие деформации противоположного знака.
Характер диаграммы состояния арматуры устанавливают в зависимости от вида арматуры.
Расчетные значения сопротивления арматуры Rs определяют делением нормативных значений сопротивления арматуры на коэффициент надежности по арматуре.
Значения коэффициента надежности следует принимать в зависимости от класса арматуры и рассматриваемого предельного состояния, но не менее:
- при расчете по предельным состояниям первой группы - 1,1;
- при расчете по предельным состояниям второй группы - 1,0.
Расчетные значения модуля упругости арматуры Es принимают равными их нормативным значениям.
Влияние характера нагрузки, окружающей среды, напряженного состояния арматуры, технологических факторов и других условий работы, не отражаемых непосредственно в расчетах, следует учитывать в расчетных прочностных и деформационных характеристиках арматуры коэффициентами условий работы арматуры γsi.
Расчетные диаграммы состояния арматуры следует определять путем замены нормативных значений параметров диаграмм на их соответствующие расчетные значения.
Интересные и нужные сведения о строительных материалах и технологиях

Нарастание прочности бетона во времени. Опыты показывают, что прочность бетона увеличивается во времени и этот процесс может продолжаться годами (рис. 1.3). Однако степень повышения прочности связана с температурно-влажностными условиями окружающей среды и составом бетона. Наиболее быстрый рост прочности наблюдается в начальный период.

Рост прочности бетона напрямую связан с его старением и поэтому зависит, по существу, от тех же факторов.
Существует целый ряд предложений по установлению зависимости между прочностью бетона R и его возрастом. Для нормальных условий твердения бетона на портландцементе наиболее простой является логарифмическая зависимость, предложенная Б.Г. Скрамтаевым:
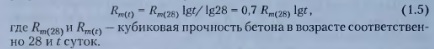
При сроках твердения, превышающих 7. 8 сут, эта формула даёт удовлетворительные результаты.
Повышение температуры и влажности среды значительно ускоряют процесс твердения бетона. С этой целью железобетонные изделия на заводах подвергают специальной тепловлажностной обработке при температуре 80 ..90 °С и влажности 90. 100 % или автоклавной обработке при давлении пара около 0,8 МПа и температуре 170 °С В последнем случае проектная прочность бетона может быть получена уже через 12 часов.
При температурах ниже +5 °С твердение бетона существенно замедляется, а при температуре бетонной смеси -10 °С практически прекращается. За 28 сут твердения при температуре -5 °С бетон набирает не более 8 % прочности бетона, твердеющего в нормальных условиях, при температуре 0 °С — 40. 50 %, при +5 °С - 70. 80%. После оттаивания бетонной смеси твердение бетона возобновляется, но конечная прочность его всегда оказывается ниже прочности бетона, твердевшего в нормальных условиях. Бетоны прочность которых к моменту замерзания составляла не менее 60% от R28, после оттаивания в течение 28 суток набирают проектную прочность.
При хранении бетона в воде наблюдается более интенсивный рост прочности. В значительной степени это объясняется тем, что в бетоне не образуются поры от испарения воды, в которых давление паров воды направлено из бетона наружу. При водяном хранении давление направлено от внешней среды в бетон.
Прочность бетона при центральном сжатии. Как следует из опытов, ссли бетонный кубнк из плотного бетона имеет достаточно однородное строение и правильную геометрическую форму, то разрушаясь под действием равномерно распределённой нагрузки он приобретает форму двух усеченных пирамид, сложенных малыми основаниями (рис. 1.4, а). Подобный характер разрушения (разрушение от среза) обусловлен значительным влиянием сил трения, которые развиваются между подушками пресса и торцовыми поверхностями образца. Эти силы направлены внутрь образца и препятствуют свободному развитию поперечных деформаций, создавая своеобразную обойму. Эффект обоймы по мере удаления от торцов образца уменьшается.
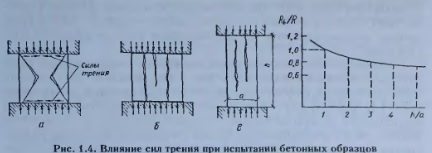
Если устранить влияние сил трения поверхностей касания (например, введением смазки на торцевых гранях образца), то разрушение приобретает иной характер (рис. 1.4, б): в образце возникают трещины, параллельные направлению сжатия. Теперь трение уже не препятствует развитию поперечных деформаций образца и разрушение происходит при гораздо меньшей (до 40 %) сжимающей нагрузке. Образцы-кубы из ячеистого и крупнопористого бетонов разрушаются по продольным поверхностям даже при наличии трения по опорным граням, поскольку связи между их структурными элементами ослаблены пустотами и порами.
Предел прочности на сжатие при испытании кубика подсчитывается делением разрушающей силы Nu на площадь грани кубика А.
В ряде стран (США и др.) вместо кубика принят образец цилиндрической формы высотой 12”(305 мм) и диаметром 6”(152 мм). Для одного и того же бетона прочность цилиндрического образца таких размеров составляет 0,8. 0,9 от прочности кубика с размером ребра 150 мм.
Прочность кубиков из бетона одного и того же состава зависит от размеров образца и уменьшается с увеличением размеров. Так, прочность кубика из тяжёлого бетона с ребром 300 мм составляет примерно 80% от прочности кубика с ребром 150 мм, а кубика с ребром 200 мм — 90%. Это объясняется как снижением эффекта обоймы при увеличении размеров образца и расстояния между его торцами, так и влиянием размеров образца на скорость твердения (чем крупнее образец, тем медленнее он набирает прочность на воздухе) и на вероятное наличие в нём внешних и внутренних дефектов (чем образец крупнее, тем, как правило, этих дефектов больше и прочность ниже).
Однако следует иметь в виду, что хотя кубиковая прочность и принята за эталон показателя прочности бетона (т.е. ее необходимо иметь для производственного контроля), она является условной характеристикой и не может быть непосоедственно использована в расчётах прочности железобетонных конструкций. Реальные конструкции (или их зоны), работающие на сжатие, по форме и размерам отличаются от кубика. В связи с этим, на основании многочисленных экспериментов установлены были эмпирические зависимости между кубиковой прочностью (классом) бетона и его прочностными характеристиками в различных условиях работы, приближающихся к работе реальных конструкций.
Опыты с бетонными образцами, имеющими форму призмы с квадратным основанием а и высотой h (рис. 1 4, в), показали, что с увеличением отношения h/a прочность при центральном сжатии Rb уменьшается (рис. 1.4, г) и при h/a > 3 становится почти стабильной и равной, в зависимости от класса бетона, 0,7. 0,9В. Это связано с тем, что в соответствии с принципом Сен-Венана напряжения, вызванные силами трения по опорным граням, существенны только в окрестности, размеры которой соизмеримы с размерами нагруженной грани. Таким образом, в призмах с высотой, превышающей двойной размер сечения, средняя часть свободна от влияния сил трения. Именно в средней по высоте части призм перед разрушением появляются продольные трещины, распространяющиеся вверх и вниз к опорным граням. Гибкость бетонного образца оказывает влияние при испытаниях только при h/a > 8.
В соответствии с указаниями ГОСТ 10180-78 прочность бетона при центральном сжатии Rh определяют испытаниями до разрушения бетонных образцов-призм с отношением высоты к стороне основания h/a = 3. 4. Нагрузку подают ступенями по 0,1 Nu с постоянной скоростью (0,6 ± 0,2) МПа/с и с 4. 5 минутными выдержками после каждой ступени.
В большинстве случаев результаты таких испытаний совершенно чётко свидетельствуют о том, что разрушение образцов происходит от преодоления сопротивления отрыву (рис 1.4, г). Однако в ряде случаев (наиболее характерно для бетонов низкой прочности, отличающихся, начальными неоднородностями, вызывающими развитие микроразрушений на ранних стадиях загружения) образец разрушается по наклонной поверхности без нарушения целостности материала вне этой поверхности. Казалось бы, можно рассматривать такие случаи как результат разрушения от среза, так как на любой площадке, пересекающей продольную ось образца под острым углом, при его нагружении возникают как нормальные, так и касательные напряжения. Но повидимому, это, всё-таки не так. И прежде всего потому, что наклон поверхности разрушения к продольной оси призмы не 45 °, что соответствовало бы направлению действия максимальных касательных напряжений, а значительно меньше (рис. 1.5). Кроме того, поверхность разрушения явно неровная, она проходит через многочисленные продольные трещины и часто совпадает с ними.
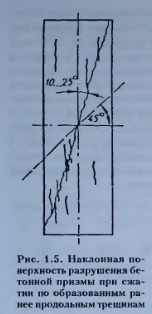
Конечно, после развития разрывов в отдельных зонах на ослабленный материал оказывают влияние касателиные напряжения, но в целом, хотя разрушение бетона здесь и носит сложный характер, определяющее значение опять-таки принадлежит сопротивлению отрыва.
Между кубиковой и призменной прочностью существует прямо пропорциональная зависимость. На основании опытных данных для тяжёлых и лёгких бетонов призменная прочность колеблется от 0,78R (для бетонов высоких классов) до 0,83R (для бетонов низких классов), для ячеистых бетонов — соответственно от 0,87R до 0,94R.
Величину Rh используют при расчёте прочности сжатых бетонных и железобетонных конструкций (колонн, стоек, сжатых элементов ферм и т. д.), изгибаемых конструкций (балок, плит) и конструкций, работающих на некоторые другие виды воздействий, например, кручение, косой изгиб, косое внецентренное сжатие и т. д.
Прочность бетона при сжатии при данной активности цемента зависит, в общем случае, от количества цемента, физико-механических свойств цементного камня и заполнителей, концентрации их в единице объема материала и прочности сцепления, а также от формы и крупности зерен заполнителей.
Увеличение количества цемента повышает плотность (отношение массы тела к его объёму) бетона, способствуя непрерывному заполнению пустот между инертными и обеспечивая тем самым создание полного несущего скелета из цементного камня. Увеличение же плотности бетона ведет, при прочих равных условиях, к повышению его прочности. Расход цемента в бетонах для несущих железобетонных конструкций колеблется в зависимости от класса бетона и активности (марки) цемента в пределах 250 до 600 кгс/м3.
Прочность цементного камня зависит не только от прочности цемента, но и от водоцементного отношения. С повышением В/Ц увеличивается пористость цементного камня, и, следовательно, падает прочность бетона.
Обычно прочность инертных в конструктивных тяжёлых бетонах выше прочности цементного камня, поэтому на прочность таких бетонов влияет лишь форма и состав зёрен заполнителей. Так, в частности, из-за лучшего сцепления раствора с угловатыми зёрнами щебня бетон на щебне примерно на 10. 15% прочнее бетона на гравии. Хуже в этом отношении ведут себя лёгкие бетоны. Так как прочность инертных в лёгких бетонах (как правило) ниже, чем цементного камня, на прочность таких бетонов влияют ещё и свойства заполнителей. Причём, в отличие от плотных пористые заполнители снижают прочность бетона и тем значительнее, чем больше отличаются Еа и Ra от Ес и Rc.
Таким образом, если прочность обычных тяжёлых бетонов зависит от ограниченного числа факторов и её можно выражать (что и делают) как функцию акти вности цемента и водоцементного отношения, то для описания прочности лёгких бетонов для каждого вида заполнителей приходится подбирать корреляционные зависимости.
Прочность бетона при растяжении. Прочность бетона при растяжении зависит от прочности на растяжение цементного камня и его сцепления с зёрнами заполнителя.
Истинная прочность бетона при растяжении определяется его сопротивлением осевому растяжению. Предел прочности при осевом растяжении сравнительно невысоки составляет (0,05. 0,1) Rb. Столь невысокая прочность объясняется неоднородностью структуры и чрезмерно ранним нарушением сплошности бетона, что способствует концентрации напряжений, особенно при действии растягивающих усилий. Величину Rbt можно определять по эмпирической формуле Фере, предложенной в своё время для бетонов низкой прочности. В настоящее время эту зависимость распространяют и на бетоны класса В45.
Прочность бетона при осевом растяжении устанавливают испытанием на разрыв образцов с рабочим участком в виде призмы достаточной длины, чтобы обеспечить равномерное распределение внутренних усилий в его средней части (рис. 1.6, а). Концевые участки таких образцов расширены для крепления в захватах. Нагрузку прикладывают равномерно со скоростью 0,05. 0,08 МПа/с.
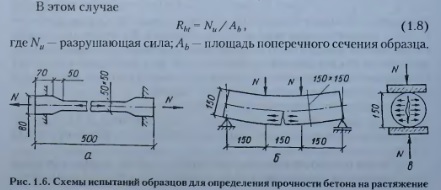
Основной недостаток испытаний на осевое растяжение — трудности, возникающие при центрировании образца, и связанный с этим большой разброс опытных данных. Так, например, захват образца в разрывной машине может создавать условия, неблагоприятные для равномерного распределения усилия по его сечению, а неоднородность структуры бетона приводит к тому, что действительная (физическая) ось образца не будет совпадать с геометрической. Оказывает влияние на результаты испытаний и напряжённое состояние бетона, вызванное его усадкой.
Чаще всего сопротивление бетона растяжению оценивают испытанием на изгиб бетонных балочек сечением 150 х 150 мм (рис. 1.6, б ). Разрушение в этом случае наступает вследствие исчерпания сопротивления растянутой зоны, причём эпюра напряжений в ней из-за неупругих свойств бетона криволинейного очертания (рис.1.7, а).
С повышением класса бетона возрастает и его прочность при растяжении, однако не столь интенсивно, как при сжатии.
Влияние различных факторов, зависящих от состава бетона и его структуры, сказывается на Rht обычно в том же направлении, что и на Rh, хотя и в неодинаковых количественных соотношениях. Так, например, повышение расхода цемента на приготовление бетона при прочих равных условиях увеличивает сопротивление разрыву в значительно меньшей степени, чем сопротивление сжатию. То же можно сказать и в отношении активности цемента . Совсем по другому обстоит дело с гранулометрическим составом заполнителей и, в частности, видом его зёрен. Так, замена гравия щебнем мало отражаясь на сопротивлении бетона сжатию, заметно увеличивает сопротивление его разрыву, и т.д.
Влияние масштабного фактора также обнаруживается при определении Rbt. Общие теоретические соображения, основанные на статистической теории хрупкой прочности, приводят к заключению, что и в этом случае следует ожидать уменьшения прочности с увеличением размеров образцов. Однако недостатки современной техники испытания бетонных образцов на растяжение (создающие рассеяние показателей тем больше, чем меньше размеры сечения) нередко искажают общую закономерность.
Величину Rbt используют, прежде всего, при расчёте конструкций и сооружений, к которым предъявляют требования трещиностойкости (например, водонапорные трубы, резервуары для хранения жидкостей, стенки автоклавов и др.).
Прочность бетона при срезе и скалывании. В соответствии с теорией сопротивления материалов действующие на элементарную площадку полные напряжения разлагаются на нормальную составляющую о и касательную составляющую т, стремящуюся срезать (сколоть) тело по рассматриваемому сечению или сдвинуть одну сторону элементарного прямоугольного параллелепипеда по отношению к другой. Поэтому напряжения т и называют напряжениями среза, скалывания или напряжениями при сдвиге.
Помимо совместного действия нормальных и касательных напряжений возможен и особый случай, известный в теории сопротивления материалов под названием чистого среза, когда о = 0 и на площадке действуют лишь скалывающие напряжения т.
В железобетонных конструкциях чистый срез практически не встречается, обычно он сопровождается действием нормальных сил.
Для экспериментального определения прочности бетона при срезе Rbsh, т.е. его предельного сопротивления по плоскости, в которой действуют только касательные напряжения, довольно долго пользовались методикой нагружения, показанной на рис. 1.8, а.
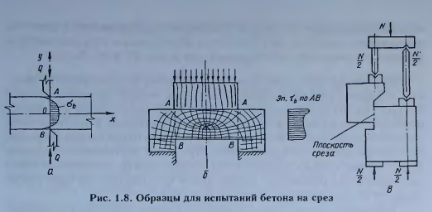
Однако решение этой задачи методами теории упругости показывает, что в плоскости АВ касательные напряжения отсутствуют. Сечение же оказывается растянутым.
Наибольшее количество опытных данных было получено при испытании по схеме, предложенной Е. Мёршем (рис. 1.8, б). Это очень простая и потому заманчивая схема, однако, как видно из характера распределения главных растягивающих напряжений в образце и касательных напряжений по сечению АВ, такой образец, кроме среза, испытывает изгиб и местное сжатие (смятие) под прокладками.
Наилучшим образом обеспечивают условия, близкие к чистому срезу, испытания по схеме А. А. Гвоздева (рис. 1.8, в). Однако и здесь картина траекторий главных напояжений говорит о том, что напряжённое состояние образца отлично от состояния, соответствующего чистому срезу. В плоскости среза действуют растягивающие и касательные напряжения, причём в местах вырезов в образце наблюдают концентрацию напряжений.
Предел прочности бетона при чистом срезе можно определять по эмпирической формуле
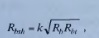
где k — коэффициент, в зависимости от класса бетона равный 0,5. 1,0.
Существенное значение при срезе имеет сопротивление крупных зёрен заполнителя, которые, попадая в плоскость среза, работают как своего рода шпонки. Уменьшение прочности заполнителей в лёгких бетонах того же класса приводит поэтому к понижению предела прочности при срезе. Предел прочности бетона при чистом срезе используют в некоторых современных методиках расчёта прочности железобетонных конструкций по наклонным сечениям.
С сопротивлением скалыванию можно встретиться при изгибе железобетонных балок до появления в них наклонных трещин. Распределение скалывающих напряжений при изгибе принимают по параболе (как для однородного изотропного тела). Опытами установлено, что предел прочности бетона па скалывание в 1,5. 2 раза выше, чем при осевом растяжении, поэтому для балок без преднапряжения расчёт на скалывание сводится, по существу, к определению главных растягивающих напряжений, действующих под углом 45° к оси балки.
Влияние на прочность бетона длительных и многократно повторных нагрузок. Одним из важнейших показателей прочности бетона следует считать его длительное сопротивление (длительную прочность), определяемое из опытов с длительным нагружением, в процессе которого бетонный образец может разрушиться при напряжениях меньших, чем его предельное сопротивление. Пределом длительного сопротивления бетона называют наибольшие напряжения, которые он может выдержать неограниченно долгое время без разрушения (для строительных конструкций это десятки лет и более).
На основании опытов принято считать, что статические напряжения, значения которых не превышают 0,8 Rb, не вызывают разрушения образца при любой длительности действия нагрузки, так как развитие возникающих в бетоне микроразрушений со временем прекращается. Если же образец нагружен большими напряжениями, то появившиеся нарушения структуры будут развиваться, и, в зависимости от уровня напряжений, через определённое время он разрушится.
Таким образом, предел длительной прочности определяется, по существу, характером структурных изменений, вызванных продолжительно действующей нагрузкой. Если процессы нарушения структуры не нейтрализуются процессами исчезновения и видоизменения дефектов, предел длительной прочности превзойден, если нейтрализуются — образец может неограниченно долго сопротивляться действующим напряжениям. Примерная граница, выше которой образец разрушается, а ниже — не разрушается, соответствует напряжениям Rvcrc. Аналогичная картина наблюдается и при растяжении.
В последние годы предложен ряд формул, позволяющих более дифференцированно подходить к оценке относительного предела длительной прочности бетона. Так, для старых тяжёлых бетонов обычных классов хорошие результаты дает формула

Если же бетон тех же классов нагружать в среднем возрасте, когда процессы твердения продолжают ещё оказывать влияние на параметр R, то длительную прочность можно определять по формуле
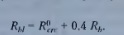
Поскольку параметры R зависят главным образом от класса бетона, его возраста в момент нагружения, роста прочности и условий влагообмепа с окружающей средой, можно считать, что и предел длительной прочности зависит в основном от тех же факторов. Так, например, относительное значение длительной прочности бетона, нагруженного в достаточно раннем возрасте, выше чем старого или малотвердеющего (прошедшего тепловлажностную обработку), а высокопрочного выше, чем бетона низкой или средней прочности.
Степень снижения длителыюй прочности зависит от продолжительности и режима предшествующих силовых воздействий. Так, длительная прочность бетона при сжатии, если он ранее находился в условиях длительного сжатия (до напряжений не более 0,6 Rh), повышается, а при растяжении — снижается.
При действии многократно повторных (подвижных или пульсирующих) нагрузок, в частности, при стационарных гармонических внешних воздействиях, предел длительной прочности бетона снижается еще больше, чем при продолжительном действии статической нагрузки. Предел прочности бетона понижается в зависимости от числа циклов нагружения, величины максимальных напряжений и характеристики цикла.
Предел прочности бетона при действии многократно повторных нагрузок называют пределом выносливости. Наибольшее напряжение, которое бетон выдерживает за бесконечно большое число повторных нагружений без разрушения, называют абсолютным пределом выносливости. Практически за предел выносливости бетона принимают максимальное напряжение, которое образец выдерживает при количестве циклов повторных нагружений, равном (2. 5) • 106 или 107. Это напряжение называют ограниченным пределом выносливости. Для бетона база испытаний принята равной 2 • 106 циклов. С увеличением ее происходит постоянное снижение предела выносливости, однако после 2 - 106 циклов изменения незначительны.

Опытные данные свидетельствуют о том, что если многократно повторно действующие напряжения превышают предел выносливости, хотя и не превышают предел длительной прочности, то при достаточном повторении циклов нагружения происходит разрушение образца. При этом разрушающие напряжения (длительная динамическая прочность) тем ниже и ближе к пределу выносливости, чем большее число циклов нагружения действовало на образец.
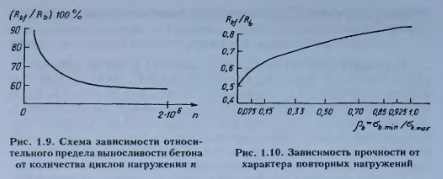
Зависимость относительного предела выносливости Rbj/Rb от числа циклов повторения нагрузки имеет криволинейный характер (рис. 1.9), приближаясь асимптотически к абсолютному пределу выносливости бетона, равному нижней границе микротрещинообразования.
При уменьшении относительный предел выносливости бетона снижается (рис. 1.10), с увеличением скорости нагружения повышается, но незначительно. Водонасыщение снижает относительный предел выносливости бетона. С увеличением возраста бетона отношение Rbf/Rb несколько увеличивается. Практический интерес представляют опытные данные о зависимости степени снижения прочности бетона при воздействии асимметричной циклической нагрузки от нижней границы микротрещинообразования в бетоне. В соответствии с этими данными значения предела выносливости пропорциональны изменению и, следовательно, отношение Rhj/Rh тем выше, чем выше прочность бетона.
Данными о пределе выносливости необходимо располагать при расчёте железобетонных подкрановых балок, шпал, станин мощных прессов и станков, фундаментов под неуравновешенные двигатели и другое оборудование, а также при расчёте элементов мостовых конструкций и разного типа транспортных, крановых и разгрузочных эстакад.
Влияние на прочность бетона высоких и низких температур. Различие в коэффициентах линейного расширения цементного камня п заполнителей при изменении температуры окружающей среды в пределах до 100 °С (т. е. стеснённые условия деформирования бетона при темперагурных воздействиях) не вызывает сколько-нибудь заметных напряжений и практически не отражается на прочности бетона.
Воздействие же на бетон повышенных температур (до 250. 300 °С) приводит к заметному изменению его прочности, причём прочность зависит от степени водопасыщения бетона. С увеличением водонасы- щения бетона при воздействии повышенных температур усиливаются процессы влаго- и газообмена, миграции влаги, происходит интенсивное высыхание бетона и образование в нем микротрещин (главным образом вследствие значительных температурных и усадочных напряжений), возрастают значения температурного коэффициента.
При действии высоких температур дело обстоит ещё хуже. При температурах свыше 250. 300 °С объёмные деформации цементного камня и заполнителей меняются. Причём, если для гранита и песчаника объёмные деформации при температуре около 500 °С резко возрастают, то для цементного камня они достигают максимума при температуре около 300 °С, а затем уменьшаются. Столь резкая разница в деформациях вызывает внутренние напряжения, разрывающие цементный камень, что влечёт за собой понижение механической прочности бетона вплоть до его разрушения. Поэтому при продолжительном действии высоких температур обычные бетоны не применяются.
Температурные напряжения можно уменьшить соответствующим подбором цемента и заполнителей. Для жаростойких бетонов применяют заполнители с малым коэффициентом линейного расширения: бой красного кирпича, доменные шлаки, диабазы и др. В качестве вяжущего используют глинозёмистый цемент или портландцемент с тонкомолотыми добавками из хромита или шамота. Для особо высоких температур (1000. 1300 °С) применяют бетоны на глинозёмистом цементе с шамотом или хромитом в качестве заполнителя.
При замораживании бетона (т. е. при действии низких температур) прочность его повышается, а при оттаивании — снижается. Определяющее влияние на прочность бетона оказывают температура замораживания и степень водонасышения бетона при его замораживании и оттаивании. Изменение прочности связано с условиями кристаллизации льда в порах бетона и возникновением в них внутреннего избыточного давления при переходе в лёд с увеличением объёма (до 10%).
Температура замерзания воды зависит от размеров пор и капилляров, в которых она замерзает. Чем меньше диаметр капилляров, тем ниже температура замерзания воды. Исследования показывают, что вода, содержащаяся в порах, замерзает не вся одновременно, а постепенно, по мере понижения температуры. Содержание льда в бетоне существенно зависит от характера его пористости. Все это говорит о том, что с понижением температуры замораживания возрастает давление в порах бетона и ускоряется его разрушение.
Существенным фактором, влияющим на прочность бетона, является наличие дефектов в его структуре в виде микро- и макротрещин. Замерзание воды в трещине и создание уже небольшого давления на её стенки вызывает концентрацию напряжений в тупике трещины и приводит к её дальнейшему прорастанию в материале.
В процессе разрушения бетона при его замораживании и оттаивании важную роль играют верхняя и нижняя условные границы микротрещинообразования.
Поскольку основной путь проникновения воды в бетон зависит от системы капилляров, повышение морозостойкости бетона следует искать, повидимому, в улучшении его структуры — уменьшении общей пористости и формировании в нём закрытой пористости вместо открытой (введение в бетон газообразующих и воздухововлекающих добавок).
Обзор статьи
Определение прочности тяжелого бетона при различных силовых воздействиях по результатам моделирования
624.012.45.04
10.23968/1999-5571-2017-14-2-107-111
Аннотация:
Приводятся данные по результатам моделирования прочностных свойств бетона при двухосном, трехосном сжатии и кратковременном динамическом нагружении. Модель разработана по результатам одноосных испытаний бетона сжимающей нагрузкой. Элементы структуры моделируются случайными величинами, распределенными по нормальному закону распределения. Выполнено сравнение результатов моделирования с известными теоретическими и экспериментальными данными.
Обзор статьи
К вопросу определения коэффициента эффективности бокового обжатия при трехосном пропорциональном сжатии тяжелого бетона
624.012.45.04
Аннотация:
Предложена модель бетона, элементы прочности которой являются случайными величинами, раcпределенными по нормальному закону. По модели рассчитана прочность бетона для характерных точек, определяющих тип разрушения бетона при трехосном сжатии. Построены графики по точкам и получены аналитические зависимости. Выполнено сравнение полученных результатов с известными литературными источниками.
Читайте также:


