Изучение дробей с помощью лего
Конструкторы LEGO — одна из любимых детских игрушек. Но оказывается, что это еще и идеальный инструмент для объяснения математики детям!
Можно придумать множество увлекательных игр на занятиях по математике, а значит, обучение будет с увлечением!
1.«Найди такую же»
Цель: Закреплять цвет, внимание, быстроту реакции.
Ход: педагог (родитель) предлагает найти деталь конструктора, которую он показывает ребенку. Усложняя игру, можно показать и убрать деталь. Тогда ребенок ищет ее по памяти.
2.«Построй пирамидку выше (ниже) моей»
Цель: знакомство (закрепление) понятий выше - ниже
Ход: предложить ребенку построить рядом с готовой, пирамидку из деталей конструктора, чтобы она была выше (ниже) образца. Усложняя можно задать цвет.
3. «Дома бывают разные»
Цель: закреплять цвет, понятия выше – ниже – одинаковые; шире – уже; развивать внимание, фантазию; конструкторские способности.
Ход: предложить детям построить городскую улицу с разными домами
4. «1,2,3,4,5 – начинаем мы считать»
Цель: знакомство с цифрами
Ход: предложить детям конструирование цифр по образцу.
Усложнение прямой и обратный счет.
5. «Больше, меньше и равно»
Цель: учить сравнивать цифры
Ход: ребенку предлагается карточки с числами, выбрав две карточки ребенок на платформе или столе выставляет две башни из лего – конструктора и сравнивает числа.
6. «Сосчитай и Найди цифру»
Цель: закреплять цифры и счет
Ход: у каждого на столе N- количество деталей Лего, ребенок считает и находит цифру соответствующую количеству деталей.
7. «Сравни узор», «Выложи такой же»
Цель: учить находить различия между двумя узорами; умение выполнить задание как в образце.
Ход: на платформах или столе выложены одинаковые узоры, ребенок должен после манипуляций с деталями узора, найти отличия. Выложить узор по схеме.
8. «Легко - Lego»
Цель: решение элементарных задач на сложение.
Ход: каждому ребенку дается карточки с примерами, с помощью лего - конструктора выстраиваются башни соответствующие цифрам, а затем соединяются в одну башню и предлагается ребенку найти цифру – ответ.
9. «Легко - Lego»
Цель: решение элементарных задач на вычитание.
Ход: каждому ребенку дается карточки с примерами, с помощью лего - конструктора выстраивается башня соответствующая уменьшаемому, а затем отсоединяются количество деталей соответствующих вычитаемому и предлагается ребенку найти цифру – ответ.
10. «Комбинаторика» (с одаренными детьми)
Цель: развитие математических способностей
Ход: предложите ребенку три кубика разных цветов. Пусть выстроит и зарисует все возможные дорожки из этих кубиков так, чтобы сочетание цветов было каждый раз разным. Требуется найти все возможные варианты решения задачи. (Подсказка - всего шесть)

Дидактические игры для обучения детей математике Конструирование с использованием «Цветных чисел» Кюизенера Цель: Упражнять детей в различении и названии цвета палочек. Развивать умение.

Дидактические игры и задания по математике Дидактические игры и задания по математике. Дидактическая игра служит для лучшего запоминания пройденного материала. Знания, полученные.

Дидактические игры по математике Представляю д/и по математике, сделанные своими руками для детей старшего возраста. Игры направленны на формирование представлений о числе.

Дидактические игры по математике своими руками Предлагаю Вашему вниманию не сложные в изготовлении игры по математике на сложение и состав числа. Цель данных игр: закрепление навыков.

Конспект занятия с использованием конструктора LEGO WeDo «Путешествие в страну LEGO» для детей подготовительной группы Цель: создание модели «Самолет» по пооперационной карте с использованием конструктора LEGO WeDo. Задачи: • обучающая: продолжать формировать.

Мастер-класс «Картотека игр по математике с использованием LEGO конструктора» Картотеки игр бывают разные! Они просто необходимы в работе воспитателя. А самое главное должны быть всегда под рукой! В основном картотеки.
НОД «Достопримечательности и театры родного города с использованием конструктора LEGO» НОД «Достопримечательности и театры родного города» с использованием конструктора LEGO Цель: представление своей модели перед аудиторией.

Дидактические игры с использованием конструктора Лего Для многих Лего ассоциируется только с конструированием и ни с чем больше. Тем не менее на основе Лего – конструирования осуществляется.

Вот нашел еще из этой же оперы про вычисление квадратов и матожидание (или среднее арифметическое).


свернула на путь гуманитария в пятом классе, как раз на теме дробей.
дурацкие торты, которые делили в учебнике на шесть кусков, выглядели неубедительно, а здесь все доступно.
эх-ма, время не вернуть)
Немного не в тему, но вспомнилась статья на хабре по переводу из двоичной системы в десятичную.


Ниночка, 26 годиков.

теперь и я понял дроби, Леша, 27 годиков )
Технарь или гуманитарий пофиг, на вкус и цвет только карандаши)
Все профессии важны, все профессии нужны 🤓
дочка учится в школе монтессори - как раз таких образом они и проходят дроби сейчас (5 лет ребенку, знает, что такое 1/2, 1/4, 1/3). Они, кстати, разные материалы используют, не только лего и специальные кубики. Школа замечательная, весь учебный материал представляется в виде игр, никого не заставляют и не пинают - всем нравится. Тут недавно заболела на неделю, через три дня уже ревела, что хочет в школу..
Не поздновато в пятом классе объяснять математику на детальках от лего? Такое ощущение что это все должно было остаться еще в первом классе.
Мне батя на мандаринах объяснял, доходчиво и вкусно!
Схоронил на будущее, может ребенок будет. Хотя кому я пизжу

на второй половине я нихуя не понял.
Мне папа на шоколадке и ее дольках объяснял
Серьёзно? Неужели у кого-то могут быть проблемы с пониманием дробей?
Спасибо. Так стало намного понятнее. Где ты был лет 15 назад?
А теперь попробуйте ребенку на LEGO объяснить, что 6/8 = 3/4
Я в детстве все никак не могла догнать, почему если ты ДЕЛИШЬ число на число 0
Ненавидел в школе дроби, на 3/4 мне стало плохо. Но обожаю дискриминант, до сих пор извлекаю из любых понравившихся чисел.
в конце поста перестал понимать где там 1/2, 2/4 и прочее
Вовочка, 27 годиков
я далеко не ребенок,но сохраню)))
я умудрился и тут запутаться, чёрт, я безнадежен
На кирпичах тоже наглядно.

Потом в голове ребенок всегда будет вспоминать лего чтобы посчитать дроби)) крутить детальки туда сюда у себя в воображении))
Прям вижу как ребенок сходу понимает почему 3/4.
никогда не понимал дроби, мне было проще 1 разделить на 4 и получить 0.25, а не кусок грёбанного ничего.
я это ещё в детстве понял
мне кажется этот способ для изначально хорошо соображающих детей, для туго соображающих надо давать наводящие задачки, чтобы ребенок сам пришел к знанию, а потом просто рассказать ему как всё это называют и изображают люди.
у немцев чуть иной подход к математике. например в делении нет скобок (рамки) которая есть у русских и всякие такие мелочи перестановки чисел. вообшем может кому то было интересно это узнать.
С нотами можно такую же тему замутить)
меня мама на чашке кофе научила выпила половину потом еще половину от половины. так и научился.
Бля. Я вроде не гуманитарий, но только сейчас понял почему дроби можно сокращать)
Кто бы меня так в свое время учил.
там не правильно блок повернут 1\4 в самой первой строчке, он должен вертикально стоять
В первом примере ошибка, или меня глючит? Там же не 1/4+3/4 = 1, а 1+4/4=1
Вот и вырастают потом такие математики, что даже с егэ не справляются.

Не хлопай


В Турции в фотоловушку попали два зайца, которые устроили файт между собой
Или просто представьте, что это срач между пикабушниками

Как у детей всё просто и невинно. Засыпает друг?
Доча , ты не видела мой Red Bull
Самые богатые супруги губернаторов

Пятый раз подряд рейтинг самых богатых супругов возглавила жена губернатора Брянской области Ольга Богомаз, заработавшая за прошлый год 389,6 млн руб. Второе место, как и последние пять лет, заняла супруга президента Татарстана Гульсина Минниханова с заработком 166,7 млн руб. На третье место вернулась старожил рейтинга — жена губернатора Ростовской области Ольга Голубева с доходом в 54,3 млн руб.
Впервые в топ-10 попала супруга губернатора Ивановской области Светлана Дрыга, заработавшая 44,8 млн руб. После четырехлетнего перерыва в рейтинге вновь жена губернатора Волгоградской области Валентина Бочарова (38,2 млн руб.). Супруга новичка губернаторского корпуса, главы Тамбовской области Евгения Егорова, попала сразу же на восьмое место с доходом в 21,3 млн руб. Из топ-10 только у нее и у супруги главы Красноярского края Людмилы Усс (20,6 млн руб.) заработки оказались ниже, чем у их мужей.
Самые богатые супруги
Главы регионов Годовой доход супруги (млн руб.)
Ольга Богомаз (супруга губернатора Брянской области Александра Богомаза) 389,6
Гульсина Минниханова (супруга главы Татарстана Рустама Минниханова) 166,7
Ольга Голубева (супруга губернатора Ростовской области Василия Голубева) 54,3
Людмила Николаева (супруга главы Республики Cаха (Якутия) Айсена Николаева) 48,1
Светлана Дрыга (супруга губернатора Ивановской области Станислава Воскресенского) 44,8
Валентина Бочарова (супруга губернатора Волгоградской области Андрея Бочарова) 38,2
Елена Аксенова (супруга главы Республики Крым Сергея Аксенова) 31,7
Евгения Егорова (супруга главы Тамбовской области Максима Егорова) 21,3
Людмила Усс (супруга главы Красноярского края Александра Усса) 20,7
Светлана Старовойт (супруга губернатора Курской области Романа Старовойта) 18,4
Самые маленькие суммы доходов в декларациях — у детей глав регионов. У Алексея Островского (Смоленская область) ребенок заработал 1,78 руб., у Валентина Коновалова (Хакасия) — 3,06 руб., у Олега Николаева (Чувашия) — 5,29 руб., у Игоря Артамонова — 13,57 руб., у Айсена Николаева (Якутия) — 17,16 руб

Антикоррупционная декларация 2021
Губернатор Брянской области Богомаз Алексей Васильевич заработал 5 220 437 руб
Талантливая жена заработала почти в 75 раз больше неудачника - мужа !
Президент Татарстана Рустам Минниханов отчитался о своих доходах и доходах своей семьи за 2021-й. В прошлом году руководитель республики заработал 8,6 млн рублей
Что меньше заработка супруги в 19.3 раза
Василий Голубев губернатор Ростовской области заработал 7.8 млн руб , что в 7 раз
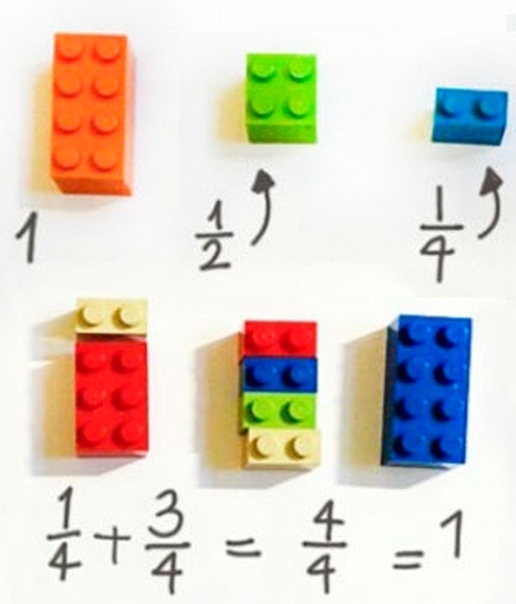
Лучший способ объяснить дроби - это банальная логарифмическая линейка.

А по старинке яблоки резать уже не модно?
Ребенок будет до конца жизни дроби в голове представлять в виде лего)
1/8 может быть и 1/1~8
Чот прокол на втором примере.
Выбесило ужасно
Решила посмотреть с ребенком обучающее видео. Автор взяла три "четверти круга" и сложила круг. Как так? Мои математические чувства задеты.

Занятия математического кружка, где занимался Г.Я. Перельман

«Это моё ноу-хау, - заявил мне Рукшин (руководитель кружка – Прим. И.Л. Викентьева) - Я понял тридцать лет назад, что необходимо выслушивать каждого ребёнка, который считает, что сумел решить задачу».
В других маткружках дети рассказывали о своих вариантах решения у доски, и дискуссия заканчивалась после первого же правильного ответа. Тактика же Рукшина заключается в том, чтобы каждый ребёнок рассказал о своём варианте решения, о своих удачах, трудностях и ошибках. Это, возможно, наиболее трудоёмкий метод обучения из существующих: ни один ученик и ни один наставник не может остаться в стороне. «Мы учим детей говорить, а преподавателей - понимать их невнятную речь и невнятные мысли».
Пока я слушала Рукшина и наблюдала за его учениками, я пыталась сформулировать своё впечатление от этих занятий. Дети увлечены сильнее, чем я когда-либо видела на занятиях других математических, шахматных, спортивных секций, но и отношения между ними напряжённей. Я потратила много месяцев на то, чтобы подобрать аналогию: занятия по методу Рукшина походят на сеансы групповой терапии. Фокус в том, чтобы в конце концов каждый ребёнок объяснил своё решение задачи всей группе. Математика для этих детей - самая увлекательная на свете вещь (иного Рукшин, похоже, и не приемлет). Они проводят большую часть своего свободного времени, размышляя над задачами, вкладывая в их решение всю свою энергию, все силы - совсем как добросовестный член анонимной группы взаимопомощи, который в перерывах между собраниями выполняет предписания тренера. На занятиях кружка дети открывают душу людям, которые так много значат для них, рассказывая о том, как они пришли к решению. […]
Возможно, дело в том, что Рукшин всегда был больше увлечён своей работой, чем любой другой преподаватель. Да, он занимался кое-какими математическими исследованиями, но математика, кажется, всего лишь побочный продукт его главного дела - воспитания участников математических соревнований мирового уровня. Эта всепоглощающая страсть и в самом деле может выглядеть и ощущаться как магия.
Волшебникам для их ремесла нужен подходящий материал: податливый, пластичный. Рукшин, у которого по многим причинам не сложилась карьера преподавателя математики, брал под свою опеку не только потенциальных вундеркиндов, но и обычных детей, чтобы доказать - он может сделать из них математиков. Неудивительно, что его внимание привлёк Гриша - не самый шумный или сообразительный, не стремящийся сильнее других к соперничеству, а самый восприимчивый.

Рукшин вспоминает, что далеко не сразу оценил мощь интеллекта Перельмана. Рукшин помогал работе жюри на некоторых районных математических олимпиадах в Ленинграде в 1976 году - просматривал листки с ответами 10-12-летних участников. В то время он искал детей со способностями к математике. Неписаные правила маткружков позволяли принимать учеников, но запрещали их переманивать. Поэтому начинающим тренерам, каким был Сергей Рукшин, приходилось искать себе учеников заблаговременно и интенсивно. Рукшину попали в руки ответы Перельмана. Они были правильными, и автор пришёл к ним не всегда обычным путём. Рукшин решил, что олимпиадные задания оказались для Перельмана слишком простыми, и предположил, что у мальчика есть будущее. Поэтому когда профессор Натансон назвал в телефонном разговоре имя своего протеже, Рукшин вспомнил его. А увидев самого Перельмана, Рукшин убедился, что в мальчике есть нечто большее, чем математическое будущее. Он увидел залог исполнения собственной мечты стать лучшим преподавателем, которого когда-либо видел свет. Рукшин сделал ставку на Перельмана - наудачу, но в случае выигрыша его ждала особая награда: а что, если ребёнок, который кажется не более талантливым, чем десятки других, превзойдет их всех?
«Когда дети изучают математику и у одного из них это получается лучше, чем у остальных, этот ребёнок получает заметно больше внимания», - Александр Голованов знает, о чем говорит. Он не только провел почти всё детство рядом с Перельманом, но и большую часть своей взрослой жизни отдал подготовке детей и подростков к математическим олимпиадам. Он - законный наследник Рукшина. Он объяснял мне, что это значит - иметь любимого ученика или быть таковым. Как и в обычных человеческих отношениях, любовь порождает преданность, преданность - отдачу, отдача - ещё большую преданность и ещё большую любовь; «Гриша был любимым учеником. Любимый ученик - это тот, с кем занимались больше других. На него потрачено больше сил». […]
Как любому тренеру, Рукшину не нравилось, когда его воспитанники отвлекались от дела, которое он считал единственно важным. Так, он вынудил уйти из своего кружка будущего чемпиона мира по шахматам Александра Халифмана, поскольку тот не мог оставить шахматы ради математики. Как и многие другие тренеры, он полагал свой вид спорта самым честным и самым красивым. Как и другие, он считал своей миссией не только тренировку своих учеников, но и воспитание их характера. Когда они взрослели, он шпионил за ними, проверяя, не занимаются ли они чем-либо посторонним и недостойным (например, не целуются ли они с девочками). Инспекции Рукшина были настолько частыми, что мальчикам казалось, будто наставник следует за ними тенью. Перельман, кстати, своего учителя не разочаровал; Рукшин не раз повторял мне, что девочки Гришу никогда не интересовали. Дважды в неделю по вечерам, после занятий кружка, Рукшин и его ученики (мальчики и несколько девочек) шли от Дворца пионеров к Витебскому вокзалу. Там Рукшин и Перельман спускались в подземку. Рукшин (он женился очень рано) жил тогда с первой женой и тёщей в Пушкине, а Гриша со своими родителями и младшей сестрой - в Купчине, на южной окраине Ленинграда, в унылой бетонной многоэтажке. Рукшин и ученики ехали в Купчино, на последнюю станцию ветки. Там Гриша выходил и шёл домой, а Рукшин садился в электричку и ещё за двадцать минут доезжал до Пушкина.

По дороге Рукшин открывал для себя Перельмана. Он узнал, например, что зимой даже в метро Гриша не развязывает уши своей шапки. «Он не просто не снимал её, но даже не развязывал тесемки, уверяя, что мать его прибьет - она попросила его никогда не снимать шапку зимой, иначе он простудится». В подземке было тепло, как дома, но вагон все же не был жилой комнатой: правила превыше всего. […]
Рукшин, наблюдая неровное развитие Перельмана, был далёк от разочарования, скорее напротив. В этой паре каждый представлял собой лучшую половину другого. Перельман мог стать непобедимым участником математических состязаний, что было не под силу Рукшину, а Рукшин умел выступить посредником между внешним миром и своим учеником, попутно защищая последнего от жизненных ударов.
Они - точнее, Рукшин - создавали ситуации, в которых один мог дополнять другого. Когда пятнадцатилетний Перельман отправился в пионерский лагерь - впервые в жизни самостоятельно, без матери, - Рукшин взял его под опеку. Следить за личной гигиеной было непросто, но все же Рукшину иногда удавалось убедить Перельмана переменить носки и нижнее бельё и спрятать грязные вещи в пакет. Стирать их он отказывался, да и сам мылся редко. Ещё он отказывался ходить купаться с другими мальчиками - отчасти потому, что не любил воду, отчасти из-за того, что не видел смысла в этом неинтеллектуальном занятии, которое к тому же не позволяло ни с кем конкурировать. Вместо этого Гриша играл в пинг-понг - и делал это замечательно. В итоге Рукшин стал использовать Перельмана как продолжение своего «я». Например, Рукшин шёл плавать с детьми, определяя самим собой границу, за которую нельзя заплывать, а Перельман оставался на берегу, пересчитывая однокашников по головам, чтобы убедиться: все на месте.
Со временем Рукшин нашёл и другие способы эффективно использовать разум Перельмана как продолжение собственного. Будучи студентом, Перельман мог проанализировать сотни и даже тысячи математических задач, выбирая задания для кружка. «На эту работу у него уходило в пять раз меньше времени, чем у меня, - вспоминает Рукшин. - Эти задания стали классикой, и никто теперь не помнит, что сделал я, а что - Перельман». Казалось, они созданы друг для друга».
Гессен М.А., Совершенная строгость. Григорий Перельман: гений и задача тысячелетия, М., «Астрель», 2011 г., с. 39-46.
Презентация к уроку математики в 5 классе по теме: Понятие обыкновенной дроби с помощью лего-конструирования"( посвященное Дню ХМАО- Югра).
| Вложение | Размер |
|---|---|
| prezentatsiya_drobi_lego.pptx | 886.02 КБ |
Предварительный просмотр:
Подписи к слайдам:
Фестивальный день! МБОУ «Лицей им. Г.Ф. Атякшева » Зуйкова Елена Викторовна Ознобихина Елена Сайпановна Урок математики в 5 Б классе.
щопщ9иоиощп Девиз урока: « Без знания дробей никто не может признаваться знающим математику» Цицерон
Проверка домашнего задания: День округа
07.12.2019 Классная работа « Понятие обыкновенной дроби с помощью лего-конструирования »
До скорой встречи!
По теме: методические разработки, презентации и конспекты

Урок математики в 5 классе "Понятие обыкновенной дроби".
На данном уроке учащиеся должны были усвоить такие понятия, как обыкновенная дробь, числитель дроби, знаменатель дроби. По типу урока, данный урок является уроком изучения нового материала, так .

Конспект урока "Понятие обыкновенной дроби"
В ходе урока рассматриваются такие понятия, как обыкновенная дробь, правила записи дроби; сокращение дробей.

Понятие обыкновенной дроби
Конспект урока по теме: "Обыкновенная дробь" с использованием ЭОР.

Познавательные метапредметные умения. 5 класс "Понятие обыкновенной дроби"
Задания для текущего контроля сформированности познавательных метапредметных действий при изучении "Понятия обыкновенной дроби" 5 класс.

Понятие обыкновенной дроби.
В тридесятом царстве, в тридесятом государстве жил был царь, и был у него сын Иван.Царь прослышал, что за тридевять земель, в некотором царстве есть какие-то дроби обыкновенные. Позвал царь Ивана и ск.

Методическая разработка ,план конспект урока по теме: "Понятие обыкновенной дроби"
Методическая разработка,план конспект урока по теме: "Понятие обыкновенной дроби".

«Апельсиновые дроби» по теме: «Понятие обыкновенной дроби»
Познакомить учащихся с понятиями « обыкновенные дроби, доли», научиться определять числитель и знаменатель дроби, понимать, что такое доля, половина, треть и четверть.


Проще ребенку на яблоке пример показать

Ооооооо крутоооо !!как раз по сольфеджио надо объяснить, что такое целая нота ,половинка, четверть и пр!:))))

Наталия, я помню как меня заставляли ходить на сольфеджио. я, вместе с вашим ребенком, тихо Вас ненавижу!)))) так и знайте!))


Дениска Редиска



David, блиииин:((( но я справлюсь с этим!:)))переживу
Наталия, не любила сольфеджио , но лишь потому, что не понимала, для чего оно нужно. Если б мне тогда показали какую-нибудь эстрадную исполнительницу и сказали бы что ,чтобы петь как она, мне надо будет написать песню , а чтобы ее написать надо учить сольфеджио, в котором объясняется как это делать, может быть с большим энтузиазмом его учила
Наталия, ну это я просто написала. Вдруг Вам поможет? А вообще может я одна не понимала для чего оно, а все другие дети понимали.
Читайте также:


